

Kopralinna raamatukogus on vaid väike virn raamatuid. Kui kobras laenab mõne raamatu, salvestab raamatukoguhoidja kopra nime ja võtab virnast pealmise raamatu. Kui kobras raamatu tagasi toob, salvestab raamatukoguhoidja taas tema nime ja paneb raamatu virna peale.
Nädala alguses olid raamatud järjestatud selliselt:

Raamatukogu selle nädala laenutuste nimekiri näeb välja selline:

Millise raamatu laenas raamatukogust Cathy?
[Raadionupud]
A. Sipsik
B. Sööbik ja Pisik
C. Tont ja Facebook
D. Kaksteist kuud
E. Krõll
Õige vastus on: B (Sööbik ja Pisik).
Cathy laenas raamatuvirna kõige ülemise raamatu, milleks oli viimasena ehk Berta poolt tagastatud raamat. Anna ja Berta alustasid laenamisega: Anna laenas "Sipsiku" virna tipust, seejärel võttis Berta järgmise raamatu ehk raamatu "Sööbik ja Pisik". Seega laenas Cathy raamatu "Sööbik ja Pisik".
Paneme tähele, et selle ülesande lahendamisel on vaja keskenduda vaid osadele ridadele laenutamiste ja tagastamisete nimekirjas: me ei pea jälgima, millise raamatu tagastas Anna või millise laenas Marta.
Raamatuvirn on tüüpiline näide pinu või magasini (ingl stack) nime all tuntud andmestruktuurist, millega pääseb juurde ainult ühest otsast (selle ülesande puhul raamatuvirna tipust). Kaks kasulikku pinuoperatsiooni on lisamine (mis lisab pinusse elemente) ja eemaldamine (mis kustutab elemente pinust). Pinul on nn LIFO (ingl Last In First Out) omadus: viimasena lisatud element on esimene, mida sellest saab eemaldada. Selles ülesandes on viimasena tagastatud raamat see, mis esimesena välja laenutatakse. Informaatikas tuntakse pinu kui kasulikku andmestruktuuri selliste andmete säilitamiseks ja korrastamiseks, millel on vajalik LIFO omadus, näiteks kasutab seda andmestruktuuri veebilehitseja "Tagasi"-nupp: viimasena külastatud leht on esimene, millele seda nuppu kasutades tagasi satutakse.

Kopra-Peetril on eriline klaviatuur salasõnumite kirjutamiseks. Mingile klahvile vajutades näidatakse ekraanil hoopis teist tähte vastavalt järgmisele joonisele:
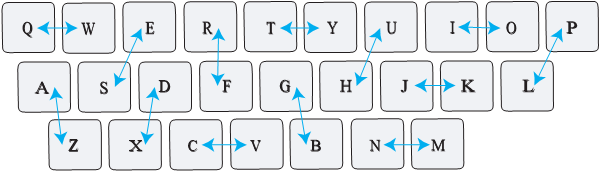
Nooled joonisel näitavad klahvide ja nende abil trükitavate tähtede vahetusi, näiteks S-klahvile vajutades ilmub ekraanile E-täht ja vastupidi.
Peetri arvutiekraan näitab teksti GSGFZE. Milline oli tegelik teade, mille Peeter kirjutas?
[Tekstikast]
Õige vastus on: BEBRAS.
Kopra-Peetri salateate saab välja uurida, kui teisendada ekraanil olevad tähed vastavalt toodud skeemile.
| G | S | G | F | Z | E | |
|---|---|---|---|---|---|---|
| saame | B | E | B | R | A | S |
Krüptograafia on üks osa arvutiteadusest. Selles ülesandes kasutatud klaviatuur põhineb asendusšifri ühel variandil, nn. Vatsyayana šifril, mille idee on pärit 4. sajandi Indiast. Vatsyayana šifri puhul luuakse tähestiku tähtedest unikaalsed paarid: ühele tähele vastab alati mõni teine täht ning iga tähte kasutatakse vaid ühes paaris. Teksti krüptimise ehk salakirjaks teisendamise ajal asendatakse iga täht tema paarilisega, dekrüptimise ehk salakirja algseks tekstiks teisendamise käigus tehakse täpselt sama operatsiooni. Tõsi, sellist salakirja on kerge lahti murda, tuginedes kasvõi tähtede sagedusele antud keeles.

Töökas kobras vajab jõele tammi ehitamiseks kuuske  , kuid tal on ainult üks porgand
, kuid tal on ainult üks porgand  .
.
Kindluses on täna kauplemispäev ja seal saab igasuguseid asju vahetada. Kobras loodab oma porgandi seal kuuse vastu vahetada.
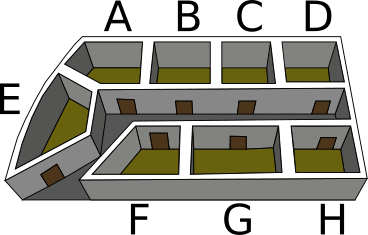
Kindluse igas ruumis on lubatud teha kaht sorti vahetusi:
| Ruum | Esimene võimalik vahetus | Teine võimalik vahetus |
|---|---|---|
| Ruum A |    |
   |
| Ruum B |    |
   |
| Ruum C |    |
   |
| Ruum D |    |
   |
| Ruum E |    |
   |
| Ruum F |    |
   |
| Ruum G |    |
   |
| Ruum H |    |
   |
Milline on selline ruumide läbimise järjekord, et kobras saaks kokkuvõttes endale kuusepuu?
[Raadionupud]
A. D-G-E
B. G-G-E
C. A-G-E
D. D-B-C
Õige vastus on: A (D-G-E).
Ruumis D vahetab kobras oma porgandi jäätise vastu, jäätise ruumis G sõrmuse ja selle omakorda ruumis E kuuse vastu.
Ruum D: 


Ruum G: 


Ruum E: 


Kui otsida sobivat ruumide järjekorda nii, et vastusevariante pole ette antud, siis võime läheneda kahel erineval viisil.
Esimene strateegia on pikem ja põhineb ideel, et porgandit saab vahetada viies ruumis (A, D, E, G ja H) kuue erineva teise objekti vastu. Nende vahetuste uurimisel tuleb arvestada kõigi järgnevate võimalustega ning nii võib tekkida isegi lõpmatu tsükkel, näiteks nii:
Ruum A: 


Ruum B: 


Ruum H: 


Ruum B: 

 - tsükkel!
- tsükkel!
Teine võimalus on rakendada sama loogikat tagurpidi. Alustame ruumist E, kuna see on ainus ruum, kust on võimalik saada kuusepuud. Selles ruumis vahetatakse kuusepuu sõrmuse vastu. Näeme, et ainuke koht, kust saaks sõrmuse, on ruum G, seal antakse see jäätise vastu. Nüüd otsime võimalusi, kuidas saada jäätist. Seda saab ruumidest B (sõrmuse vastu) ja D (porgandi vastu). Kuna kopral on porgand, siis viimane neist variantidest ongi sobiv.
Ülesandes antud vahetusvõimalused saame esitada ka suunatud graafina. Iga tipp kujutab objekti ja iga kaar tippude vahel vastavas ruumis tehtavat vahetust:

Selline visuaalne esitus lubab mugavamalt leida tee porgandi ja kuuse vahel, nii saame kergesti kontrollida, et DGE on õige vastus.
Arvutiteaduses kasutatakse suunatud graafe palju, näiteks programmi võimalike olekute visualiseerimiseks (nn. "lõplikud automaadid"). Ülesannete teisendamine graafiks aitab neid lahendada graafi-põhiste stateegiate abil. Väiksema graafi, nagu selles ülesandes, võime lihtsalt välja joonistada ja lahendus on silmaga näha.
Suuremate graafide puhul see nii lihtne ei ole. Arvuti abi kasutamiseks on vaja lahendusviis kirjeldada süstemaatilise algoritmina. Üks võimalikke variante on graafi läbimine sügavuti. Nii võime alustada porgandist ja vaadata iga tipu puhul järjest läbi, kuhu me sealt edasi liikuda saame, ja siis kuhu sealt edasi, kuni jõuame kuuseni. Sellise lähenemise puhul peab olema ettevaatlik, et mitte sattuda lõpmatusse tsüklisse (näiteks ABHBHBH...).

Koprakülas elab 12 kobrast. Igal kopral on oma urg ja urud on omavahel ühendatud nööridega, mida koprad kasutavad teadete saatmiseks.
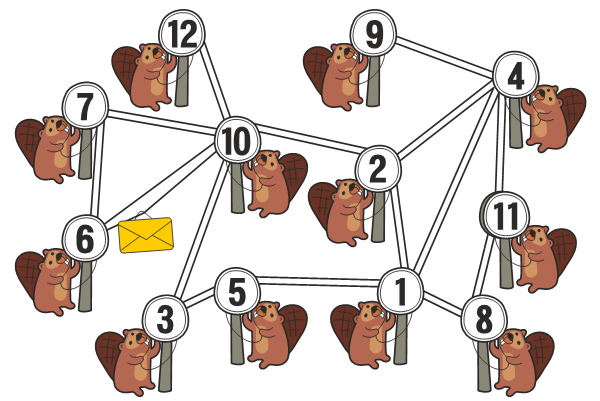
Koprad tahavad igast sündmusest võimalikult kiiresti teada saada. Kui üks neist kuuleb põnevat uudist, saadab ta selle kõigi enda uru juures olevate nööride kaudu teistele edasi. Näiteks kui 8. urus elav kobras saab teada midagi uut, kuulutab ta seda kobrastele 1. ja 11. urus. Järgmised, kes seda uudist kuulevad, on 2., 4. ja 5. urus elavad koprad jne, kuni kõik koprad on uudisest teada saanud.
Millises urus elavale koprale peaksime uudise teatama, et see jõuaks kõigi kobrasteni nii kiiresti kui võimalik?
[Täisarv [1, 12]]
Õige vastus on: 2.
Kui uudis teatada 2. urus elavale koprale, jõuab see kõigi teisteni kahe sammuga. Esimesel sammul saavad teate 4., 1. ja 10. urus elavad koprad, nemad teatavad sellest kõigile teistele. Kõik urud on 2. urust kõige rohkem kahe sammu kaugusel. Pole ühtki teist urgu, mille puhul oleks võimalik sama kiirus, rääkimata veelgi lühemast teest.
Palju reaalelulisi probleeme on lahendatavad graafi abil. Graaf koosneb tippudest ja neid ühendavatest servadest. Selles ülesandes on vaja leida graafi nn tsenter.
Tsentriks nimetatakse tippu või tippe, mille puhul kaugus neist kõigi teiste graafi tippudeni on kõige väiksem. Meie ülesandes on ainult üks sobiv tipp, nimelt tipp ehk urg numbriga 2.
Tsentri leidmine on kasulik näiteks teenuste asukoha valimisel, et teenuse kaugus seda vajavast elanikust oleks võimalikult väike ka halvimal juhul. Näiteks haigla paigutamine linna keskele vähendab aega, millega kiirabiauto jõuab kõige kaugema majani linnas.
Kui graaf on väike (nagu käesoleva ülesande puhul), on selle keskpunkti leidmine võimalik lihtsalt proovimise abil. Suuremate graafide puhul tuleb kasutada targemaid algoritme, näiteks Floyd–Warshalli algoritmi.

Kobras Robert töötab firmas Pagarikoprad. Ta vastutab külas leiva klientidele kojuviimise eest. Robert tahab sõita võimalikult vähe. Seepärast uurib ta kaarti, kuhu on märgitud leiba tellinud klientide majad, ning leida marsruudi, mille puhul külastab ta iga kliendi kodu ainult ühe korra ning mille puhul läbib ta iga tänavat maksimaalselt ühe korra. Samuti peab ta arvestama, et sõit algab ja lõpeb kohas, mis on kaardil tähistatud punase punktiga.
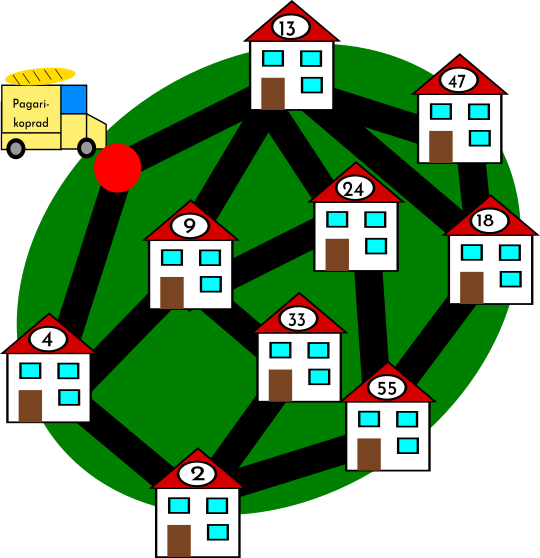
Millises järjekorras peaks Robert KÕIGI klientide majad läbi sõitma?
[Raadionupud]
A. 4-2-55-18-47-13-24-9-4
B. 4-9-33-2-55-18-47-13-9-4
C. 13-9-24-47-18-55-2-33-4
D. 13-47-18-55-24-9-33-2-4
Õige vastus on: D (13-47-18-55-24-9-33-2-4).
Variandis A (4-2-55-18-47-13-24-9-4) külastatakse maja 4 kaks korda, samas jääb vahele maja 33.
Variandis B (4-9-33-2-55-18-47-13-9-4) puudub maja 24, samas maju 4 ja 9 külastatakse kaks korda.
Variandis C (13-9-24-47-18-55-2-33-4) puudub tee majade 24 ja 47 ning 33 ja 4 vahel.
Informaatikas kohtume tihti graafiteooriaga seotud ülesannetega, kuna graafi kasutatakse sageli andmete esitamiseks. Selles ülesandes esindavad majad graafi tippe, tänavad aga selle servi. Me otsime nn. Hamiltoni tsüklit ehk teed graafis, mille puhul külastatakse iga tippu täpselt ühe korra ning kus tee algus ja lõpp on samas kohas.

Jaak on kortermaja majahoidja. Majas on viis korterit, igas elab üks kobras. Tööle minnes jätavad koprad võtmed Jaagu kätte. Et võtmed segi ei läheks, kasutab Jaak iga võtme jaoks eraldi sahtlit, mille peal on kirjas omaniku nime kolm esimest tähte.

Turvalisuse kaalutlustel pole võtmetel kirjas nimed. Selle asemel on Jaak kirjutanud iga võtme kleebisele 3 numbrit, mis on seotud omaniku nime kolme esitähega. Kõigi võtmete puhul vastab igale tähele sama number.
Kord kukkus võtmesahtlite kapp ümber; võtmed läksid segi ja üks kleebis kadus ära.
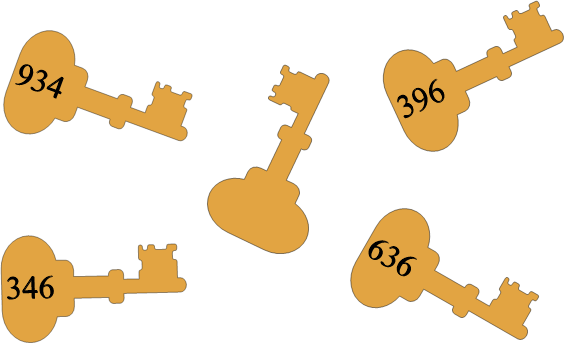
Milliste numbritega kleebis läks kaduma?
[Täisarv]
Õige vastus on: 496.
Sahtel BEB on ainuke, mille puhul on esimene ja kolmas täht samad, järelikult peab sellele vastama võti numbriga 636. Seega me teame, et täht "B" vastab numbrile 6 ja täht "E" numbrile 3. Sahtel AER peab siis vastama võtmele, mille keskmine number on 3 ning mille viimane number peab erinema teistest (ülejäänud sahtlite viimane täht on "B"). Seepärast peab selle võtme kood olema 934 ning seega vastab tähele "A" number 9 ja tähele "R" number 4. Nii saame teada, et EAB kood on 396 ja ERB kood 346. Järele jääb sahtel RAB ning sellele vastab kombinatsioon 496.
Krüptograafia on tähtis osa informaatikast. Selles ülesandes kasutatud vastavus põhineb asendusšifri ühel variandile, nn. Vatsyayana šifril, mille idee on pärit 4. sajandi Indiast. Vatsyayana šifri puhul luuakse tähtede ja numbrite unikaalsed paarid: ühele tähele vastab alati mõni kindel number ning iga tähte kasutatakse vaid ühes paaris. Teksti krüptimise ehk salakirjaks teisendamise ajal asendatakse iga täht talle vastava numbriga, dekrüptimise ehk salakirja algseks tekstiks teisendamise käigus tehakse vastupidi. Sellist salakirja on kerge lahti murda: teades üht tähe ja numbri paari, annab see meile palju infot edasiseks dešifreerimiseks. (Pane tähele, et kuigi ülesanne on pealtnäha üsna erinev, on selle aluseks olev informaatikaidee sama, mis ülesandel "Saladuslikud klahvid".)

Kobras leidis vana salakoodi kirjelduse.
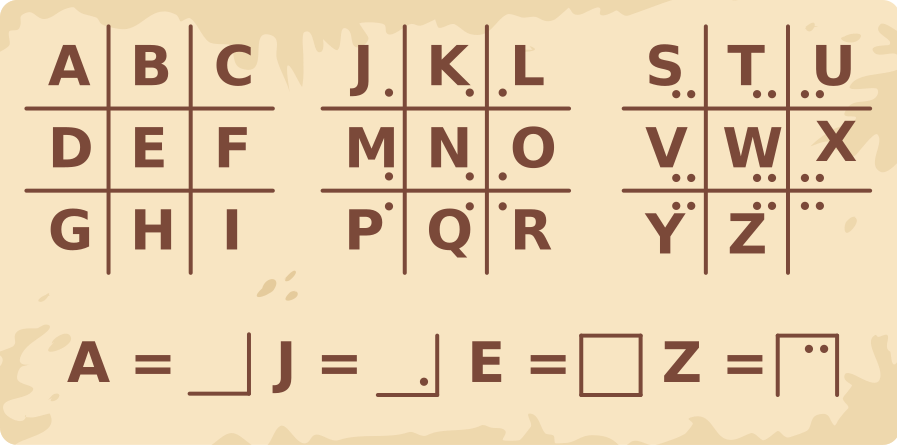
Milline sõna on kirjutatud allolevas reas?
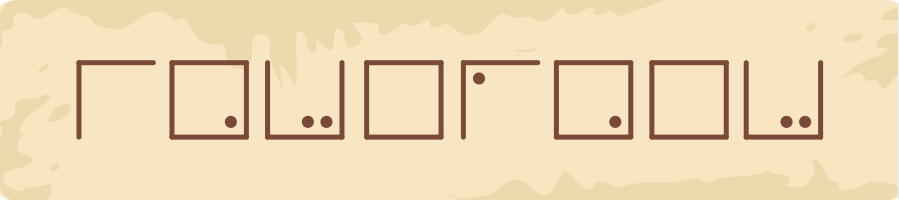
[Tekstikast]
Õige vastus on: INTERNET.
Sõnas on kasutatud viit erinevat tähte. Esmalt võib üle lugeda täppide arvu, et otsustada, millisest tabelist on vaadeldav sümbol pärit, seejärel otsustada raamide järgi, millist konkreetset tähte on mõeldud.
Ülejäänud tähed kordavad eelmisi ning on vastavalt N, E ja T.
See ülesanne sisaldab lihtsat salakirjasüsteemi. Salakirja eesmärk on hoida sõnumi sisu saladuses nende eest, kes ei peaks seda infot teadma. Kui sa soovid saata mingit sõnumit oma sõbrale, kes istub klassis sinust kaugemal, võid kirjutada teksti paberile ja saata selle oma klassikaaslaste abil sõbrale. Kui sa aga soovid, et teised peale sinu ja su sõbra sellest sõnumist aru ei saaks, võid selle salastada koodi või šifri abil, mida teate vaid teie kaks.
Sõnumite šifreerimine on vajalik ka näiteks arvutivõrkudes, et hoida saladuses paroole ja muud tundlikku infot, mis pole mõeldud teistele arvutivõrgus olevatele seadmetele. Informaatika osa, mis tegeleb salakirjandusega, nimetatakse krüptograafiaks.
Šifreid on sõnumite krüptimiseks kasutatud aastatuhendeid. Enamik vanadest šifritest on arvutite abil kergesti lahti murtavad. Arvutid suudavad proovida lühikese aja jooksul palju erinevaid võimalusi ning suure tõenäosusega leida võtme teksti avamiseks. Tänapäevased šifrid on palju keerulisemad ning sageli ka väga põnevad.

Kopraoja tänava elanikud otsustasid oma valged majad ära värvida. Lepiti kokku järgmised reeglid:
Nagu pildil näha, on mõned majad juba värvitud.

Millist värvi peab oma maja värvima Kopra-Siim?
[Raadionupud]
A. Kindlasti punast värvi
B. Kindlasti sinist värvi
C. Kindlasti rohelist värvi
D. Kopra-Siim võib valida nii sinise kui rohelise värvi
Õige vastus on: B (sinine).
Õige vastuse saame leida näiteks sellise arutluskäiguga.
Värvime kõigepealt need majad, mille puhul on naabrite tõttu ainult üks variant:

Nüüd keskendume Kopra-Siimu tänavapoolele. Vasakult teise maja naaber on sinist värvi ja temast üle tänava asub roheline maja, seega peab see olema punane:

Samasugustel põhjustel peab kolmas maja olema roheline:

Seega saab Siimu maja olla ainult sinist värvi:

Kümme maja kokku moodustavad graafi, mis esitab nende omavahelisi seoseid:

Graaf koosneb tippudest (joonisel ringid) ja servadest (jooned ringide vahel). Selles ülesandes tähistab iga tipp maja ja iga serv suhet "on kõrvuti" või "on otse üle tänava". Pane tähele, et värvimise reeglite seisukohalt on mõlemat liiki suhted samaväärsed.
Ülesandeks on värvida tipud nii, et ükski serv ei ühendaks sama värvi tippe. See on klassikaline graafiülesanne ja alati ei pruugi saada hakama vaid kolme värviga. Aga on teada, et kui graaf kujutab kaardil olevaid naabreid (näiteks maju või riike), ei ole selle värvimiseks kunagi vaja rohkem kui neli värvi.
Informaatikas kasutatakse graafe paljude erinevate ülesannete modelleerimiseks. Samuti on aegade jooksul loodud palju algoritme, mille abil graafiülesandeid arvutiga lahendada.

"Maod ja redelid" on Eestis tuntud lauamängu "Tsirkus" eelkäija. Kõik mängijad alustavad ruudust number 1 ja võidab see, kelle nupp jõuab esimesena viimasesse ruutu ehk ruutu 49. Käimiseks veeretab mängija tavalist täringut (mis annab 1 kuni 6 silma) ja liigutab oma nuppu niimitu ruutu edasi.
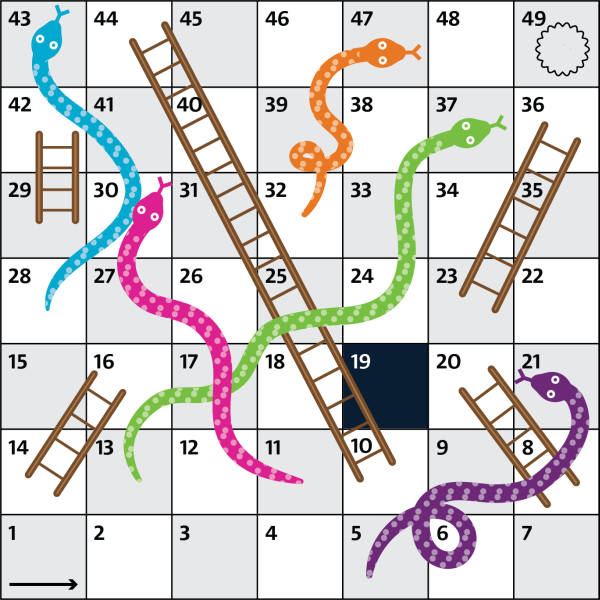
Kui mängija nupp peatub käigu lõppedes mao peaga ruudul, viiakse see tagasi ruudule, kus on mao saba, näiteks ruutu 21 maandudes viib madu nupu ruutu 5. Redelid seevastu aitavad kiiremini edasi liikuda: kui nupp satub käigu lõppedes redeli alumisele otsale, tõstetakse see redeli ülemise otsa juurde (näiteks ruudust 23 ruutu 36).
Milline on minimaalne täringuvisete arv, millega ruudus 19 olev nupp võib viimasesse ruutu jõuda?
[Raadionupud]
A. 2
B. 3
C. 4
D. 5
Õige vastus on: B (3).
Kui liikuda ainult edasi, siis kulub minimaalselt 4 viset: ruudust 19 saab ühe viskega ruutu 23, sealt viib redel ruutu 36 ning edasi (kuna rohkem redeleid teel pole) tuleb visata veel vähemalt 3 korda (näiteks 6, 6 ja 1).

Siiski on ka lühem variant, kui liikuda madude abil ka tagasi: ruudul 19 olles tuleb visata 2 ja kukkuda ruudult 21 ruudule 5. Siis tuleb visata täringuga 5 ja, kasutades pikka redelit, ronida ruudult 10 ruudule 44. Seejärel piisab vaid ühest täringuviskest (5), et jõuda lõppu. Nii piisab võitmiseks vaid kolmest viskest.

Võimatu on võita 2 viskega, kuna esimese viske järel võib maanduda ruutudel 20, 5, 22, 36, 24 või 25 (visates täringuga vastavalt 1 kuni 6). Ühestki neist ruutudest pole võimalik jõuda järgmise viskega viimasele ruudule.
See on lühima tee leidmise ülesanne. Mängulauda võib kujutada graafina, kus ruudud on tipud ja serv kahe tipu vahel tähendab, et nende kahe ruudu vahel on võimalik liikuda ühe täringuviskega. Nüüd otsime lühimat (vähima arvu servade läbimist nõudvat) teed nupu lähtetipust sihttippu.
Lühima tee otsimiseks sobib nn. laiuti läbimise algoritm: alustame lähtetipust ja vaadatame läbi kõik selle naabertipud (esimene täringuvise). Kui nii sihttippuni ei jõuta, vaadame läbi kõik esimese käigu järel leitud tippude naabrid (teine täringuvise) jne.

Kopra-Karin soovib joonistada pilte ilma pliiatsit paberilt tõstmata, liikudes ühest punktist teise ja joonistades iga lõiku täpselt ühe korra.
Näiteks saab ta nende reeglite järgi joonistada maja sellisel viisil:

Millist algjärgnevatest kujunditest SAAB Karin nende reeglite järgi joonistada?
[Raadionupud]
A. 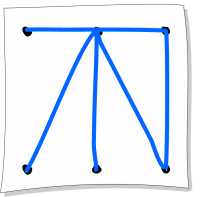
B. 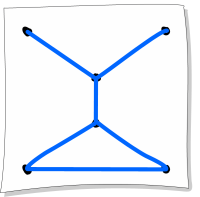
C. 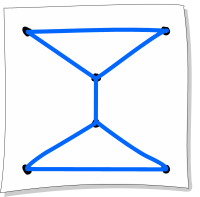
D. 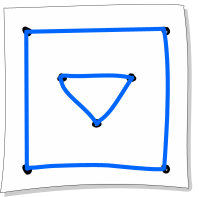
Õige vastus on: C.
Üks võimalus kujundi C joonistamiseks:

Paneme tähele, et kujundil C on täpselt kahe punkti küljes paaritu arv jooni (joonisel näpuga näidatud).
Kujundil A on selliseid punkte neli, kuid meil saab joonistamisel olla vaid üks alguspunkt ja üks lõpp-punkt. Igasse vahepealsesse punkti läheme ühe joonega sisse ja teisega seal välja. Sellepärast saabki paaritu arvu joontega punkt olla ainult joonistamise algus või lõpp. Kui meil oleks lubatud jooni mitu korda joonistada, poleks see probleem, kuid meie reeglid on teistsugused.

Kujundil B on sama mure: näiteks vasakult ülevalt alustades saaks me hargnemiskohal minna kas alla või paremale üles, kuid mõlemal juhul peaks me kujundi lõpetamiseks tuldud teed tagasi tulema.

Variant D koosneb kahest eraldi kujundist ning kuna neid ükski joon ei seo, ei saa seda ilma pliiatsit tõstmata joonistada.
Toodud kujundid koosnevad punktidest ja joontest nende vahel. Informaatikas on see üks võimalus esitada objekte ja nende vahelisi suhteid. Sellist kujutamisviisi nimetatakse graafiks, mis koosneb tippudest ja neid ühendavatest servadest.
Graafi, milles leidub tee igast tipust igasse teise (võimalik, et ka muid tippe läbides), nimetatakse sidusaks. Graafi on võimalik ühe joonega joonistada siis ja ainult siis, kui see on sidus ja selles on kas null või kaks tippu, mille küljes on paaritu arv servi.
Graafi iga serva täpselt üks kord läbivat teed nimetatakse Euleri teeks, kuulsa matemaatiku Leonhard Euleri (1707-1783) järgi, kes esimesena kirjeldas seda ülesannet Königsbergi seitsmel sillal jalutamise näitel. Arvutis leitakse Euleri teed Fleury või Hierholzeri algoritmiga.

Kaarel teeb geograafiatunniks referaati ja tahab sinna lisada joonise Eesti linnade rahvaarvude kohta. Ta kaalub joonisele mitut kujundust, aga tegi ühe variandi juures vea.
Milline järgmistest joonistest EI ESITA ülejäänutega samu andmeid?
[Raadionupud]
A. 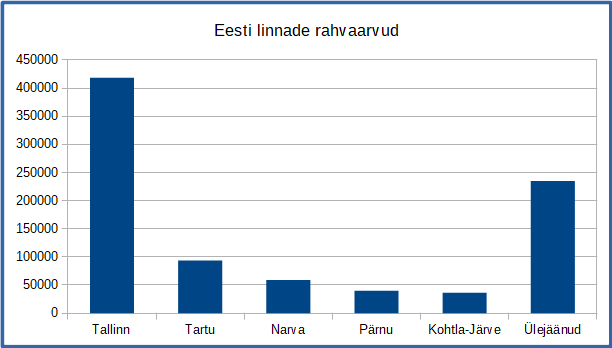 B.
B. 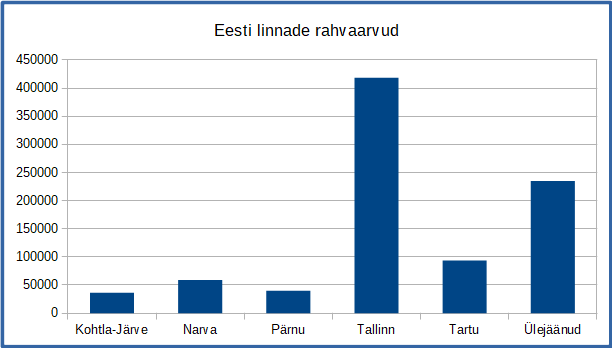
C. 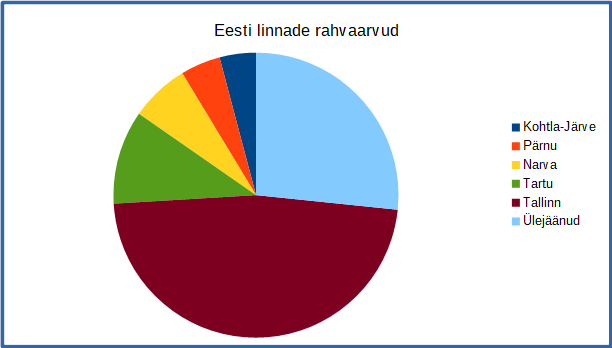 D.
D. 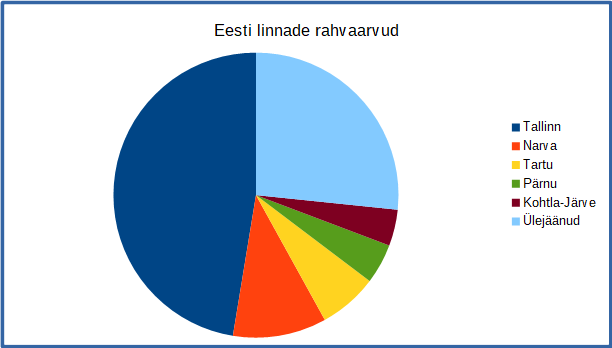
Õige vastus on: D.
Kõigil teistel joonistel on Tartu rahvaarv Narva omast suurem (mis on ka faktiliselt õige), aga joonisel D on see vastupidi.
Sama informatsiooni on sageli võimalik kujutada mitmel erineval moel. Aga isegi kui andmetes endis vigu ei ole, on mõned esitused paremini aru saadavad kui teised. Näiteks rahvaarvu järgi järjestatud jooniselt A on kohe näha, et Narva on Eesti suuruselt kolmas linn, samas nimede järgi järjestatud jooniselt B on selle väljalugemine märksa tülikam.
Muidugi, kui joonise eesmärk ongi näidata mingi suuruse muutumist ajas, nagu allpool on tehtud Tartu rahvaarvuga erinevatel aastatel, on just tulpade järjestamine nende kõrguse järgi vähem ülevaatlik.


Näidetes kasutatud andmed pärinevad Wikipediast.

Astridi väikevend luges suvel raamatut "Karlsson katuselt" ja kirjutas sellest emakeeletunniks kokkuvõtte.
Viimasel hetkel märkas Astrid, et väikevend on paljudes kohtades kirjutanud "Karlsson" asemel "Karlson". Seejuures esineb Karlssoni nimi väikevenna töös mitmes erinevas käändes ning on mõnes kohas kirjutatud õigesti ja mõnes kohas valesti.
Kuidas saab Astrid aidata väikevennal vea kiiresti ja vähese vaevaga parandada?
[Raadionupud]
A. Laseb tekstitöötlusprogrammil asendada teksti "so" kõik esinemised tekstiga "sso"
B. Laseb tekstitöötlusprogrammil asendada teksti "Karlson" kõik esinemised tekstiga "Karlsson"
C. Seda ei saa teha funktsiooni "otsi ja asenda" ühe kasutusega, tuleb otsida ja asendada iga käänet eraldi
D. Eesti keele käänete tõttu ei saa seda üldse "otsi ja asenda" funktsiooniga parandada, tuleb kogu tekst hoolikalt üle lugeda
Õige vastus on: B.
B on õige vastus, sest sõna "Karlson" käänamisel selle tüvi ei muutu. Teksti "Karlson" asendamisel tekstiga "Karlsson" asendatakse õigesti ka "Karlsoni" → "Karlssoni", "Karlsonit" → "Karlssonit" ja nii edasi ka kõik ülejäänud käänded.
A ei ole õige, sest nii tehes muutuks juba õigesti kirjutatud "Karlsson" vigaseks variandiks "Karlssson", samuti näiteks "Majasokk" → "Majassokk".
C oleks õige vastus, kui oleks vaja teha parandus mingis sõnas, mille tüvi käänamisel muutub, näiteks kui sõnas "õde" erinevates käänetes ("õde", "õe", "õele", ...) oleks "õ" asemel kogemata "ö" kirjutatud. Karlssoni nimi käänamisel nii palju ei muutu ja sellepärast saab seda lihtsamalt parandada.
D oleks õige vastus, kui meie valesti kirjutatud sõna võiks mõnes teises kontekstis olla ka õige sõna või selle osa. Näiteks kui tekstis esineb ka sõna "öeldis", siis lihtne asendus "öe" → "õe" rikuks selle ära. Paljudes tekstitöötlusprogrammides on selliste olukordade lahendamiseks "otsi ja asenda" fuktsioonil võimalik määrata, et asendatakse ainult terveid sõnu. Aga siiski on võimalik, et ka sellest lahendusest ei piisa ja tulebki kõik kahtlased kohad ükshaaval üle vaadata.
Arvutid on küll kiired ja täpsed käsutäitjad, aga käsu andmisel peab alati meeles pidama, et arvuti teeb täpselt seda, mida kästud, isegi kui see ei ole see, mida kasutaja tahtis. Suur osa informaatikast ja eriti programmeerimisest seisnebki just selles, et välja mõelda, kuidas oma soove arvuti jaoks piisavalt täpselt sõnastada.

Bioloogiatunniks teeb Kaarel referaati lindudest ja loomadest. Referaadi sisukorda ei tee ta käsitsi, vaid laseb selle genereerida tekstitöötlusprogrammil.
Selleks märgib ta imetajate ja lindude peatükkide pealkirjad laadiga Pealkiri 1 (ingl Heading 1). Töös vaadeldud imetajate (rebane, hunt, jänes, kobras) jaotiste pealkirjad märgib ta laadiga Pealkiri 2 (ingl Heading 2). Kobraste jaotises on kaks alamjaotist, mis on ka sisukorras kajastatud.

Täna lisas Kaarel referaati jäneste jaotisse alamjaotised valgejänesest, halljänesest ja ameerika jänesest.
Kuidas peaks nende pealkirjad vormistama, et nad sisukorras õigesti kajastuksid?
[Raadionupud]
A. Need peaks märkima laadiga Pealkiri 1
B. Need peaks märkima laadiga Pealkiri 2
C. Need peaks märkima laadiga Pealkiri 3
D. Need peaks märkima laadiga Pealkiri 4
Õige vastus on: C.
Number pealkirja laadis vastab üksuse tasemele dokumendi struktuuris. Peatükid kui kõrgeima taseme üksused on number 1, nende sees olevad jaotised number 2 ja nende sees olevad alamjaotised number 3. Kui alamjaotiste sees oleks omakorda pealkirjastatud lõike, oleks nende taseme number 4.
Arvutid on tänapäeval veel üsna nõrgad vabas vormis andmete töötlemisel ja soovitud tulemuse saamiseks peavad kasutajad sageli ise lisama oma andmetele märkusi selle kohta, kuidas neid töötlema peaks. Kuigi see võib alguses tunduda tarbetu lisatööna, on see pikemas plaanis aja ja vaeva kokkuhoid.
Näiteks kui pealkirjadele on laadid märgitud, saab nende kõigi kujundust korraga muuta, andes käsu ühe või teise laadiga pealkirju erinevalt vormistada. Kui pealkirjadel laadimärke küljes ei oleks, peaks dokumendi autor iga pealkirja kujundust eraldi muutma. Esiteks on see rohkem tööd ja teiseks kaasneb sellega ka risk, et mõni pealkiri jääb vahele ja pärast on dokument ebaühtlase stiiliga.

Kobras Priidul on lõpmatu arv pusletükke. Tükid on kaheteistkümne erineva kujuga ja kolme erinevat värvi:
| Värv | Tükid |
|---|---|
| PUNANE |  |
| KOLLANE |  |
| SININE |  |
Neid tükke kasutades saab ta luua erinevaid värvide järgnevusi, näiteks:
SININE → KOLLANE → KOLLANE → PUNANE → KOLLANE → SININE → KOLLANE → KOLLANE

Iga järgnevus peab algama algustükiga (tükiga, mille vasak äär on sirge) ja lõppema lõputükiga (tükiga, mille parem äär on sirge). Järgnevuste koostamisel ei tohi Priit omavahel kokku panna tükkide sirgeid ääri.
Millist toodud järgnevust EI SAA konstrueerida Priidu pusletükkidest?
[Raadionupud]
KOLLANE → SININE → SININE → PUNANE → PUNANE → PUNANE → SININE
SININE → KOLLANE → PUNANE → KOLLANE → PUNANE
PUNANE → PUNANE → KOLLANE → SININE → SININE → SININE
SININE → PUNANE → KOLLANE → SININE → PUNANE → KOLLANE → PUNANE
Õige vastus on: C.
Priit ei saa ühendada ühtki sinist tükki sinise lõputükiga, seepärast järgnevust C ta koostada ei saa.
Selles ülesandes peab kombineerima pusletükke kindlasse järjekorda. Mõned kombinatsioonid sobivad, mõned mitte. Samuti on ka informaatikas: kui erinevaid elemente kombineeritakse, siis kehtivad reeglid, millised kombinatsioonid on lubatud, millised mitte.
Käesolevas ülesandes on reeglid ette antud tükkide kujudena, kuid sageli on küllalt keeruline otsustada, kas järgnevus vastab reeglitele või mitte: kas näiteks mingi programmiosa poolt antud väljund on sellisel kujul, mida järgmine osa saab kasutada. Üldiselt on programmid väga jäigad ja teatavad vigasest sisendist, kuid mõnikord püütakse ka valel kujul sisendist võimalikult hästi aru saada. Heaks näiteks on veebibrauserid, kus eeldatakse, et kasutaja soovib saada infot isegi siis, kui veebilehel esineb tehnilisi vigu.

Mati tahab avaldada kooli veebilehel õpilaste küsitluse tulemuste tulpdiagrammid. Kujundustarkvara võimaldab salvestada pilte mitmes vormingus.
Millist allolevatest vormingutest peaks diagrammide jaoks kasutama?
[Raadionupud]
Õige vastus on: D (PNG).
Pakutud variantidest on diagrammide veebis esitamiseks sobivaim vorming PNG. See on rastergraafika vorming, mis tähendab, et iga pilt esitatakse väikeste erivärviliste ruudukestena. PNG vorming kasutab kadudeta pakkimist, mis tähendab, et lahtipakkimisel saame tagasi täpselt esialgsed andmed. See vorming on sobiv suurte ühtlast värvi või korduva mustriga pindade ja kontrastsete joontega "kunstlike" jooniste esitamiseks, nagu diagrammid ongi. Ka on PNG vorming toetatud kõigis tänapäevastes veebilehitsejates nii arvuti- kui ka tahvli- ja telefoniopsüsteemides.
JPEG on samuti rastervorming, kuid kasutab kadudega pakkimist. JPEG on loodud, et esitada "naturaalseid" pilte, näiteks fotosid, kus on palju erinevaid toone ja sujuvaid üleminekuid nende vahel. Kontrastsete teravate joontega piltidel põhjustab selles vormingus kasutatav pakkimisalgoritm üsna suuri moonutusi, nagu näha allolevas võrdluses. Sellepärast ei ole see vorming kuigi sobiv "kunstlike" piltide (graafikud, joonised, erkaanitõmmised) jaoks.
BMP on kadudeta rastervoming, nagu ka PNG, kuid kasutab palju lihtsamat pakkimisalgoritmi, mistõttu on selles vormingus failid palju suuremad kui saaksime sama pilti PNG vormingus salvestades. Näiteks ühe umbes 600x350 pikseli suuruse tulpdiagrammi faili maht PNG vormingus on umbes 8 KB, aga BMP vormingus üle 600 KB. Lisaks on BMP Windowsi-spetsiifiline vorming ja ei tarvitse kõigi opsüsteemide veebilehitsejates toetatud olla.
EPS on kõigist eelnevatest erinevat vektorgraafika vorming. See tähendab, et EPS-failis kirjeldatakse pilti mitte ruudukujulistest pikselitest mosaiigina, vaid joontest, ristkülikutest, ringidest jmt geomeetrilistest objektidest koosnevana. Tänu sellele saab vektorvormingus pilte suurendada ja vähendada ilma, et nende kvaliteet sellest muutuks. Allolevas võrdlustabelis on näha, et PNG ja BMP vormingus pildid muutuvad suurenamisel ruuduliseks ning JPEG vormingus pilt läheb uduseks, aga vektorvormingus pilt jääb endiselt teravaks. EPS vormingu puudus on, et see on ajalooliselt trükitööstuses kasutusel olnud väga keeruline vorming ja ei ole veebilehitsejates toetatud (selles vormingus piltide vaatamiseks on vaja lisaprogrammi).
Tänapäevane ja ka veebis kasutamiseks mõeldud vektorgraafika vorming on Scalable Vector Graphics (*.svg). Sellel on üldiselt EPS vorminguga sarnased positiivsed omadused ja kui diagrammide koostamise tarkvara seda vormingut toetab, on see enamasti parim valik. Siiski tasub silmas pidada, et see on üsna uus ja veel arenev failivorming ning mõnede keerulisemate jooniste puhul võib juhtuda, et kõik veebilehitsejad ei oska neid päris õigesti näidata.
| PNG/BMP (suurendus) | JPEG (suurendus) | SVG/EPS (suurendus) |
|---|---|---|
 |
 |
 |
Kui samu andmeid on võimalik esitada mitmes erinevas vormingus, nagu see näiteks graafika puhul on, siis peab õige vormingu valimiseks teadma iga vormingu tugevaid ja nõrku külgi.
Copyright © 2020 Bebras – International Challenge on Informatics and Computational Thinking.
Licensed under Creative Commons Attribution-ShareAlike 4.0 International License.
Flag icons by GoSquared.