

В библиотеке Бобруйска имеется небольшая стопка книг. Когда бобр берёт книгу, то библиотекарь записывает его имя и выдаёт из стопки верхнюю книгу. Когда бобр возвращает книгу, то библиотекарь вновь записывает его имя и кладет книгу наверх стопки.
В начале недели книги были упорядочены следующим образом:

Список движения книг на этой недели выглядит следующим образом:

Какую книгу Катя взяла из библиотеки?
[Raadionupud]
A. Хоббит
B. Фантазёры
C. Маленький принц
D. Книга джунглей
E. Хроники Нарнии
Правильный ответ: B (Фантазёры).
Катя взяла из стопки книг самую верхнюю, которая была возвращена самой последней. Эту книгу вернула Белла. Анна и Белла первыми взяли книги из библиотеки: Анна взяла расположенного на самом верху "Хоббита", после чего Белла взяла следующую книгу, то есть "Фантазёров". Таким образом, Катя взяла книгу "Фантазёров".
Обратим внимание на то, что при решении данного задания необходимо сосредоточиться только на части списка: мы не должны отслеживать какую книгу вернула Анна или взяла Марина.
Стопка из книг - это типичный пример структуры данных под названием стек (англ. stack). Доступ к нему возможен только с одной стороны (в данном задании только сверху). Двумя важными операциями в работе со стеком являются добавление (элемент добавляется в стек) и удаление (элемент удаляется из стека). Стек обладает так называемым LIFO (англ. Last In First Out) свойством: последний добавленный элемент является первым, который может быть удалён. В данном задании последняя возвращённая книга будет той, которую возьмут из библиотеки первой. В информатике стек является полезной структурой данных для хранения и упорядочивания таких данных, в отношении которых можно применить свойство LIFO. Например, в браузере стек используется в работе кнопки "Назад": последняя посещённая страница будет первой, на которую пользователь попадает при нажатии на эту кнопку.

У бобра Пети имеется особая клавиатура для написания зашифрованных сообщений. При нажатии на клавишу на экран выводится совершенно другая буква, но согласно следующему рисунку:
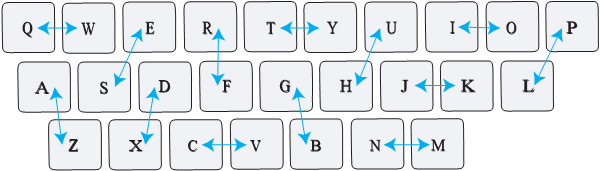
Стрелки на рисунке показывают происходящие замены между клавишами и печатаемыми с их помощью буквами. Например, нажав на клавишу S, на экране появится буква E и наоборот.
На экране Пети виден текст GSGFZE. Что на самом деле написал Петя?
[Tekstikast]
Правильный ответ: BEBRAS.
Зашифрованное сообщение бобра Пети можно узнать, если заменить имеющиеся на экране буквы в соответствии с приведённой схемой.
| G | S | G | F | Z | E | |
|---|---|---|---|---|---|---|
| получим | B | E | B | R | A | S |
Криптография является составляющей частью компьютерных наук. В этом задании работа клавиатуры основывается на принципах работы одного из шифров подстановки - так называемом шифре Ватсьяяна (англ. Vatsyayana). Идея этого шифра возникла в 4 веке в Индии. При использовании шифра Ватсьяяна из букв алфавита формируются уникальные пары: одной букве всегда соответствует какая-нибудь другая буква и каждая буква используется только в одной паре. При шифровании, то есть кодировании тайного сообщения, каждая буква заменяется парной ей буквой; при расшифровке, то есть раскодировании тайного сообщения в первоначальный текст, делается точно такая же операция. Правда такое тайное сообщение очень легко взломать, например, зная частоту букв в данном языке.

Трудолюбивому бобру для постройки плотины на реке нужна ель  , но у него имеется только одна морковь
, но у него имеется только одна морковь  .
.
Сегодня в замке проходит ярмарка, на которой можно обменяться различными вещами. Бобр решил отправиться туда со своей морковью в надежде обменять её на ель.
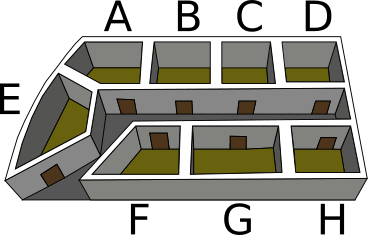
В каждой комнате замка разрешено провести два вида обмена:
| Комната | Первый возможный обмен | Второй возможный обмен |
|---|---|---|
| Комната A |    |
   |
| Комната B |    |
   |
| Комната C |    |
   |
| Комната D |    |
   |
| Комната E |    |
   |
| Комната F |    |
   |
| Комната G |    |
   |
| Комната H |    |
   |
В какой последовательности необходимо пройти комнаты, чтобы бобр в итоге смог получить ель?
[Raadionupud]
A. D-G-E
B. G-G-E
C. A-G-E
D. D-B-C
Правильный ответ: A (D-G-E).
В комнате D бобр сможет поменять свою морковь на мороженое, далее в комнате G мороженое поменять на кольцо, которое в свою очередь в комнате E можно поменять на ель.
Комната D: 


Комната G: 


Комната E: 


Если искать подходящую последовательность комнат без использования предложенных вариантов ответов, то можно это сделать двумя способами.
Первая стратегия более длинная и основывается на идее обмена моркови в пяти комнатах (A, D, E, G и H) на шесть различных объектов. При изучении такого обмена необходимо учитывать все последующие возможности и таким образом может даже возникнуть бесконечный цикл. Например,
Комната A: 


Комната B: 


Комната H: 


Комната B: 

 - цикл!
- цикл!
Вторая возможность - это применить ту же логику, но наоборот. Начнем с комнаты E, так как она единственная комната, где можно получить ель. Здесь можно ель обменять на кольцо. Видим, что единственным местом, где можно было бы получить кольцо, является комната G, где его дают в обмен на мороженое. Далее ищем возможности получения мороженого. Его можно получить в комнатах B (в обмен на кольцо) и D (в обмен на морковь). Так как у бобра имеется морковь, то подходящим является последний вариант.
Приведенные в задании возможности обмена можно представить в виде ориентированного графа. Каждая вершина представляет собой объект и каждая дуга между вершинами демонстрирует обмен, который можно провести в соответствующей комнате:
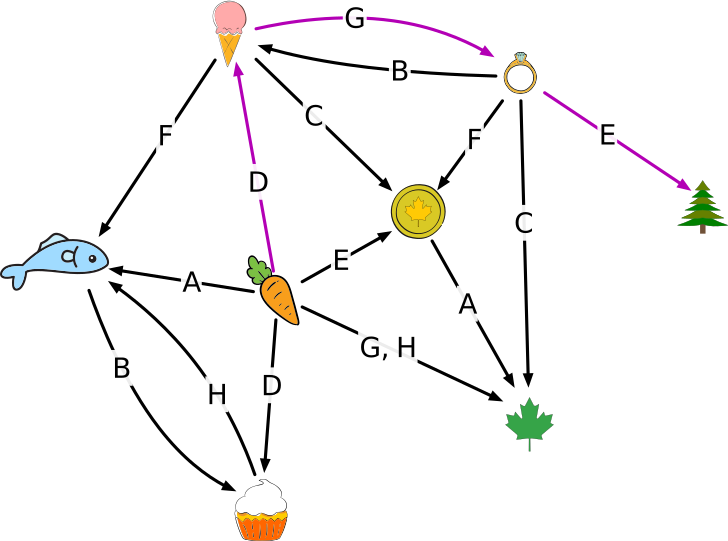
Такое визуальное представление позволяет удобно найти путь между морковью и елью, также можно легко проверить, что DGE является правильным вариантом.
В компьютерных науках используется очень много ориентированных графов. Например, для визуализации возможных состояний программы (так называемые "конечные автоматы"). Преобразование заданий в графы позволяет найти их решения с помощью основанных на графах стратегий. Маленький граф, как в случае нашего задания, можно просто нарисовать и глазами увидеть решение.
В случае больших графов это уже не так легко. При использовании помощи компьютера способ решения необходимо описать в виде систематического алгоритма. Одним из возможных вариантов является прохождение графа в глубину. Таким образом, можем начать с моркови и для каждой вершины последовательно изучить путь продвижения до тех пор, пока не получим ель. В таком случае следует быть очень внимательным и осторожным, чтобы не попасть в бесконечный цикл (например, ABHBHBH...).

В деревне живет 12 бобров, и у каждого из них есть своя нора. Все норы соединены между собой верёвками, которые бобры используют для передачи сообщений.
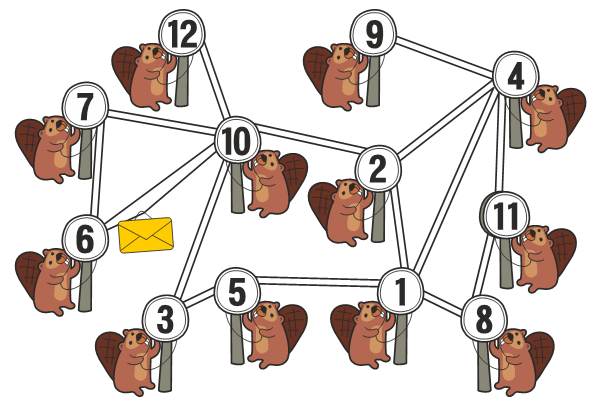
Бобры хотят как можно быстрее узнать о каждом произошедшем событии. Как только один из них узнаёт горячую новость, он тут же отправляет её другим бобрам с помощью расположенных рядом с его норой верёвок. Например, если живущей в 8ой норе бобр узнаёт что-то новое, то он информирует об этом живущих в 1ой и 11ой норах бобров. Следующие, кто узнает эту новость, будут живущие в норах 2, 4 и 5 бобры. И так далее, пока эту новость не получат все бобры.
Бобру из какой норы следует сообщить новость, чтобы она достигла всех остальных бобров как можно быстрее?
[Täisarv [1, 12]]
Правильный ответ: 2.
Если новость сообщить бобру, живущему во 2ой норе, то она достигнет всех остальных за 2 шага. После первого шага эту новость будут знать бобры, живущие в норах 4, 1 и 10. Далее они передадут эту новость всем остальным. Все норы находятся от 2ой норы на расстоянии не более двух шагов. Не существует ни одной другой норы, которая позволила бы достичь такую же скорость, не говоря уже о более коротком пути.
Множество жизненных проблем решаются с помощью графов. Граф состоит из вершин и соединяющих их рёбер. В данном задании следует найти так называемый центр графа.
Центром называется вершина или вершины, расстояние от которой до всех остальных вершин графа будет самым маленьким. В нашем задании имеется только одна такая подходящая вершина, и это вершина под номером 2.
Определение центра является полезным, например, при выборе местоположения услуг. Расстояние от потребителя до места оказания услуг должно быть по возможности маленьким и в менее удачных случаях. Например, расположение больницы в центре города уменьшает время, за которое машина скорой помощи доедет до самого отдаленного дома в городе.
Если граф маленький (как, например, в данном задании), то определение центральной точки возможно путем перебора. В случае больших графов следует использовать более умные алгоритмы, например, алгоритм Флойда — Уоршелла (англ. Floyd–Warshall algorithm).

Бобр Роберт работает в фирме "Бобры-пекари". Он отвечает за доставку хлеба к клиентам домой. Роберт хочет проезжать как можно меньшее расстояние. С этой целью он решил изучить карту, на которой отмечены дома клиентов, куда он обязательно должен отвезти хлеб. Он решил составить такой маршрут, чтобы быть около дома каждого клиента только один раз и проезжать каждую улицу максимально один раз. Также он должен учитывать, что поездка должна начинаться и заканчиваться в отмеченной красным цветом точке.
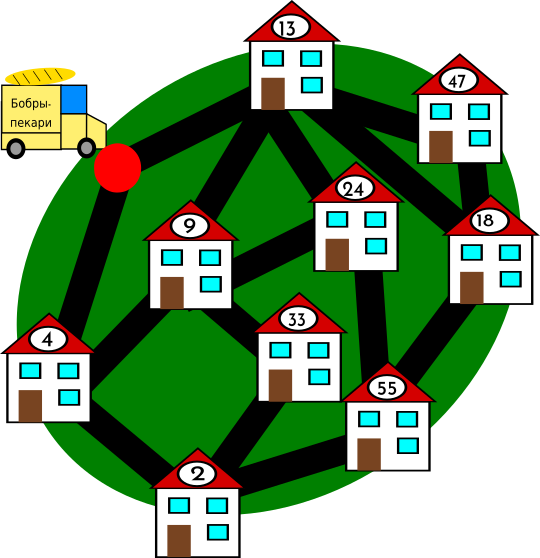
В каком порядке следует Роберту проехать ВСЕ дома клиентов?
[Raadionupud]
A. 4-2-55-18-47-13-24-9-4
B. 4-9-33-2-55-18-47-13-9-4
C. 13-9-24-47-18-55-2-33-4
D. 13-47-18-55-24-9-33-2-4
Правильный ответ: D (13-47-18-55-24-9-33-2-4).
В варианте A (4-2-55-18-47-13-24-9-4) дом 4 проезжается два раза, но остается в стороне дом 33.
В варианте B (4-9-33-2-55-18-47-13-9-4) отсутствует дом 24, а дома 4 и 9 проезжаются два раза.
В варианте C (13-9-24-47-18-55-2-33-4) отсутствует дорога между домами 24 и 47, а также 33 и 4.
В информатике часто встречаются задачи на теорию графов, потому что графы часто используются для представления данных. В этом задании дома выступают в роли вершин графов, а улицы в роли рёбер. Мы искали так называемый гамильтонов цикл, то есть путь в графе, каждая вершина которого посещается только один раз, и где начало и конец пути находятся в одном и том же месте.

Жан работает портье в квартирном доме, где расположено пять квартир. В каждой квартире живёт по одному бобру. Когда бобры уходят на работу, то оставляют ключи Жану. Чтобы ключи не перепутались, он использует для каждого ключа отдельный сундучок, на котором указаны первые три буквы имени хозяина.

В целях безопасности на ключах не указаны имена хозяев. Вместо этого на каждый ключ Жан прикрепил наклейку с 3 цифрами, которые связаны с первыми тремя буквами имени хозяина. Для всех ключей каждой букве соответствует та же цифра.
Однажды полка с сундучками упала, и ключи перемешались. К сожалению, потерялась и одна наклейка.
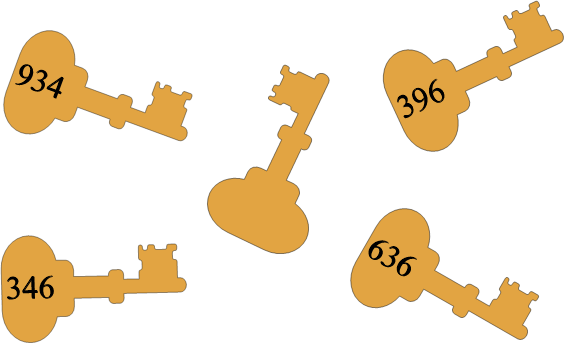
Наклейка с какими цифрами потерялась?
[Täisarv]
Правильный ответ: 496.
Сундучок BEB является единственным, где первая и третья буквы одинаковые. Значит, здесь хранится ключ с цифрами 636. Теперь мы знаем, что букве "B" соответствует цифра 6, а букве "E" цифра 3. В сундучке AER должен храниться ключ, у которого средняя цифра будет 3, и у которого последняя цифра должна отличаться от других (в случае оставшихся сундучков последней буквой является "B"). Таким образом, на этом ключе должна быть наклейка с цифрами 934. Теперь мы также знаем, что букве "A" соответствует цифра 9, а букве "R" цифра 4. Значит, сундучку EAB соответствует ключ с цифрами 396, а сундучку ERB ключ с цифрами 346. Остался только сундучок RAB, которому соответствует комбинация 496.
Криптография является важной частью информатики. В этом задании применённое соответствие основывается на одном варианте шифра подстановки - так называемом шифре Ватсьяяна (англ Vatsyayana). Идея этого шифра возникла в 4 веке в Индии. При использовании шифра Ватсьяяна из букв и цифр формируются уникальные пары: одной букве всегда соответствует конкретная цифра и каждая буква используется только в одной паре. При шифровании текста, то есть кодировании тайного сообщения, каждая буква заменяется парной ей цифрой; при расшифровке, то есть раскодировании тайного сообщения в первоначальный текст, делается обратная операция. Правда такое тайное сообщение очень легко взломать: зная одну пару буквы и цифры, получаем очень много информации для дальнейшей расшифровки. (Обратите внимание, что несмотря на то, что на первый взгляд задания кажутся совершенно разными, в их основе лежит одна и та же идея информатики, что и в задании " Таинственные клавиши").

Бобрёнок нашел описание старого кода.
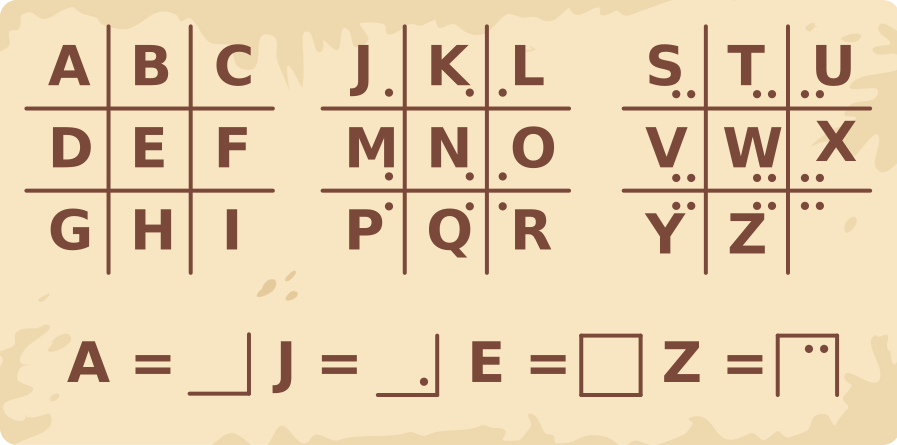
Какое слово записано на приведённой ниже строке?
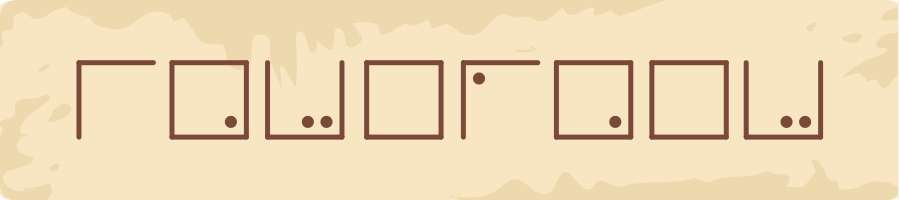
[Tekstikast]
Правильный ответ: INTERNET.
В слове использовано пять различных букв. Сначала необходимо посчитать количество точек, чтобы определить, в какой таблице находится рассматриваемый символ. Далее по границам можно узнать, какая конкретная буква имелась в виду.
Остальные буквы повторяют предыдущие, соответственно N, E и T.
Это задание содержит простую систему шифрования. Цель шифрования - держать содержимое сообщения в секрете от тех, кто не должен знать эту информацию. Если ты хочешь отправить какое-нибудь сообщение другу, который в классе сидит далеко от тебя, можешь написать текст на бумажку и с помощью одноклассников передать другу. Однако, если ты хочешь, чтобы никто другой кроме тебя и твоего друга не смогли разобраться в тексте сообщения, то можешь зашифровать его с помощью кода или шифра, который знаете только вы двое.
Шифрование сообщений происходит, например, в компьютерных сетях, чтобы держать в секрете пароли и другую важную информацию, которая не предназначена для других расположенных в компьютерной сети устройств. Часть информатики, которая занимается шифрованием, называется криптографией.
Тысячелетиями для криптования сообщений использовались шифры. Большинство старых шифров можно легко взломать с помощью компьютера. За короткий промежуток времени компьютеры могут перебрать большое количество вариантов и с большой долей вероятности подобрать ключ для расшифровки сообщения. Современные шифры намного сложнее, а также очень интересные.

Жители улицы Бобринской решили выкрасить свои белые дома в другие цвета. Между собой они договорились, что:
Как видно на картинке, часть домов уже покрашена.

В какой цвет должен выкрасить свой дом бобр Саша?
[Raadionupud]
A. Обязательно в красный цвет
B. Обязательно в синий цвет
C. Обязательно в зелёный цвет
D. Бобр Саша может выбрать синий или зелёный цвет
Правильный ответ: B (синий).
Правильный ответ можем найти, например, с помощью следующих шагов.
Прежде всего покрасим те дома, где из-за уже выкрашенных соседский домов можно использовать только один вариант:
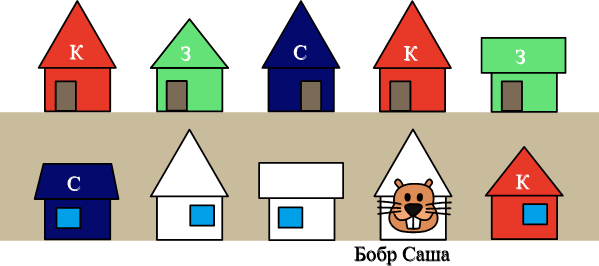
Теперь посмотрим на ту сторону улицы, где стоит дом Саши. От второго дома с левой стороны стоит покрашенный в синий цвет дом, а напротив этого белого дома через улицу стоит зелёный дом. Значит, этот белый дом должен быть выкрашен в красный цвет:
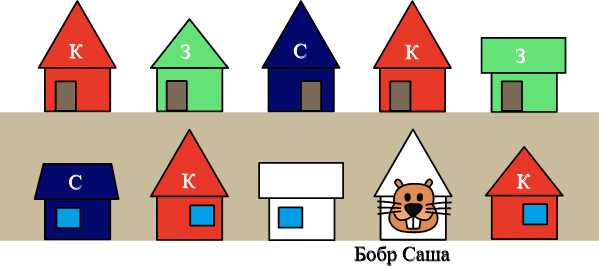
Рассуждая таким же образом, узнаем, что третий дом должен быть выкрашен в зелёный цвет:
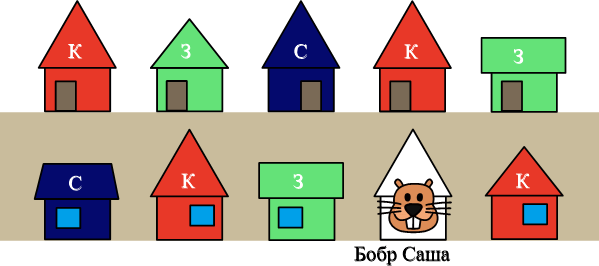
Таким образом, цвет дома Саши может быть только синим:
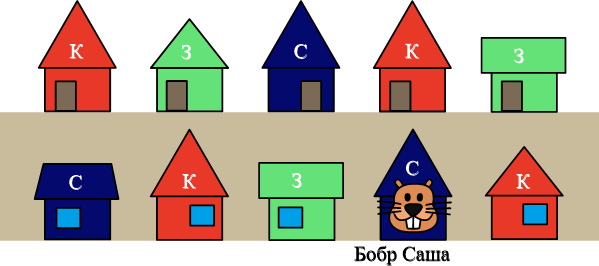
Десять домов образуют граф, который демонстрирует связи между домами:
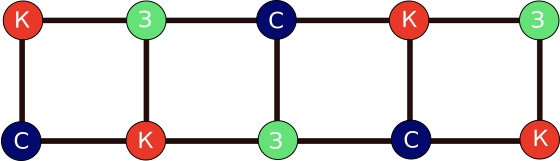
Граф состоит из вершин (на рисунке представлены в виде кружков) и рёбер (линии между кружками). В данном задании каждая вершина - это дом, а каждое ребро - отношение "рядом" или "через дорогу напротив". Обратите внимание, что с точки зрения выбора цветов, отношения этих двух типов эквивалентны.
Суть задания заключается в покраске вершин таким образом, чтобы ни одно ребро не соединяло вершины одинакового цвета. Это классическое задание на работу с графом, и не всегда можно справиться с помощью трёх цветов. Однако известно, что если с помощью графа представить расположенные на карте соседей (например, дома или страны), то для их раскрашивания никогда не понадобится более четырёх цветов.
В информатике графы используются для моделирования различных заданий. Также со временем были разработаны различныве алгоритмы, которые позволяют с помощью компьютера решить задания с графами.

"Змеи и лестницы" является популярной в Эстонии настольной игрой. Все игроки начинают с клетки, обозначенной номером 1. Выигрывает тот, чья фишка первой достигнет последней клетки, то есть клетки с номером 49. Во время своего хода игрок бросает игральную кость, на которой может выпасть от 1 до 6 очков, и передвигает свою фишку на выпавшее на кости число клеток.
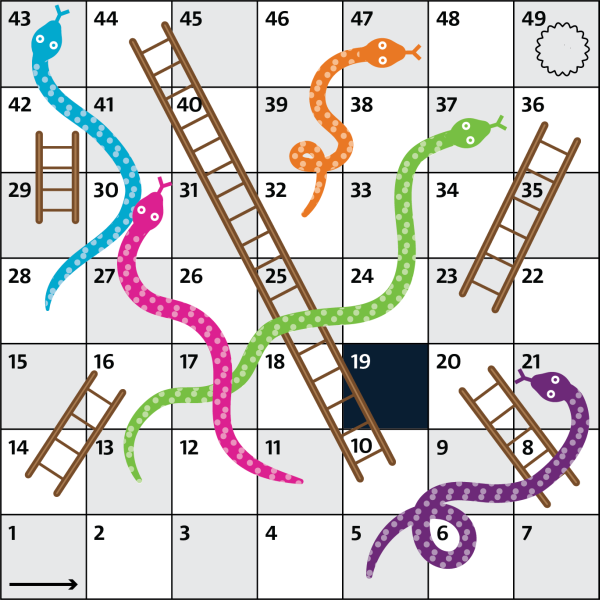
Если в конце хода фишка игрока оказывается на клетке с головой змеи, то фишка перемещается на клетку, где находится хвост змеи. Например, оказавшись на клетке с номером 21, фишка перемещается на клетку с номером 5. Имеющиеся лестницы наоборот позволяют передвигаться по полю быстрее: если в конце хода фишка оказывается в нижнем конце лестницы, то она переносится на верхний конец лестницы (например, с клетки 23 на клетку 36).
Какое наименьшее число бросков игральной костью надо сделать, чтобы фишка с клетки 19 оказалась на самой последней клетке?
[Raadionupud]
A. 2
B. 3
C. 4
D. 5
Правильный ответ: B (3).
Если двигаться только вперёд, то понадобится 4 броска: за один бросок с клетки 19 можно попасть на клетку 23, а оттуда уже на клетку 36. Дальше на пути больше нет лестниц и придётся сделать по меньшей мере 3 броска (например, 6, 6 и 1).
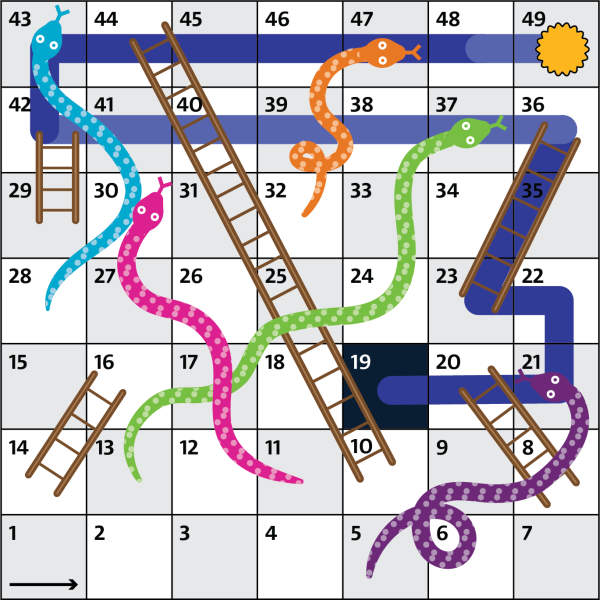
Однако есть и более короткий вариант, если с помощью змей двигаться в обратном направлении: находясь на клетке 19, необходимо бросить кость так, чтобы выпало 2 очка. Оттуда с клетки 21 фишка перемещается на клетку 5. После этого необходимо выбросить на кости 5 очков и, используя длинную лестницу, переместиться с клетки 10 на клетку 44. Далее будет достаточно одного броска игральной костью (5 очков), чтобы добраться до конца. Таким образом, для победы будет достаточно сделать три броска.
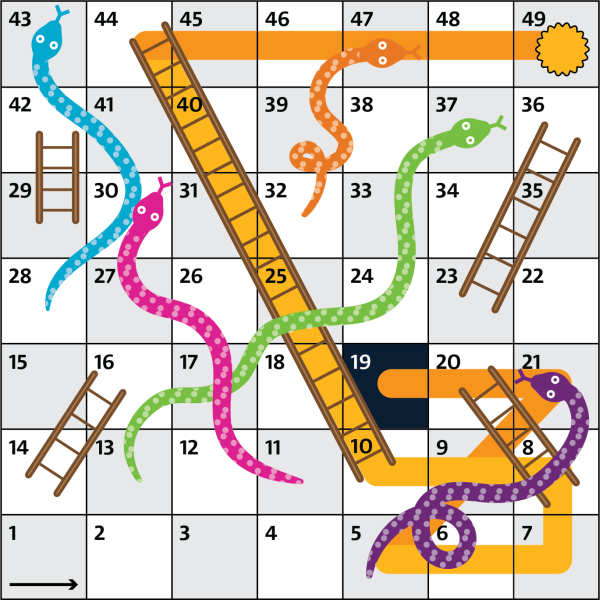
Невозможно выиграть за 2 броска, потому что после первого броска фишка может оказаться на клетках 20, 5, 22, 36, 24 или 25 (получая на кости соответственно очки от 1 до 6). Ни с одной из этих клеток за следующий бросок игральной кости невозможно добраться до последней клетки.
Это задание на нахождение наименьшего пути. Игровой стол можно представить в виде графа, где клетки - это вершины, а ребро между двумя вершинами означает, что между этими двумя клетками можно переместиться после одного броска игральной кости. Далее следует найти наикратчайший (требующий прохождения наименьшего количества рёбер) путь от исходной вершину до конечной вершины.
Для поиска наикратчайшего пути подходит так называемый алгоритм поиска в ширину: начинаем с исходной вершины и просматриваем все соседние с ней вершины (первый бросок игральной кости). Если мы ещё не оказались на конечной вершине, то опять просматриваем все соседние вершины, которые есть у найденных после первого броска вершин (второй бросок игральной кости) и т.д.

Бобрёнок Катя хочет нарисовать рисунок, не отрывая карандаша от бумаги и перемещаясь по каждому отрезку, соединяющему две точки, только один раз.
Например, следуя этим правилам, она может нарисовать дом следующим образом:

Какую из нижеприведённых фигур Катя СМОЖЕТ нарисовать, придерживаясь установленных правил?
[Raadionupud]
A. 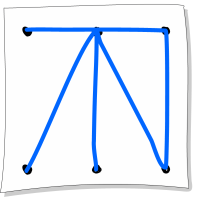
B. 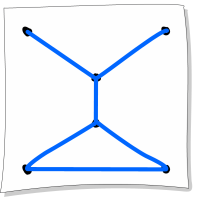
C. 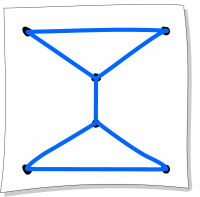
D. 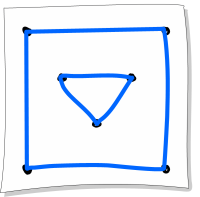
Правильный ответ: C.
Чтобы нарисовать фигуру C, можно воспользоваться, например, следующим способом:

Обратите внимание на то, что у фигуры C непосредственно в двух точках сходится нечётное количество линий (на рисунке эти места отмечены пальцами).
У фигуры А таких точек четыре, но у нас во время рисования может быть только одна начальная точка и одна конечная точка. В каждую промежуточную точку заходит одна линия и выходит тоже одна. Поэтому точка с нечётным количеством линий может быть только началом или концом рисования. Если бы было разрешено линию рисовать несколько раз, то это не было бы проблемой, но в задании указаны другие правила.
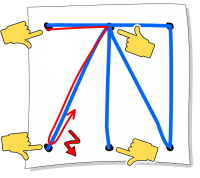
В случае фигуры B такая же проблема: например, начиная с верхней левой точки и дойдя до точки разветвления, мы можем дальше пойти вниз или к верхней правой точке. Однако в любом случае для завершения фигуры мы должны будем вновь пройти уже нарисованный путь.
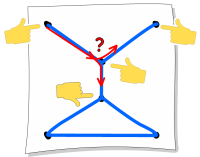
В случае варианта D имеется две отдельных фигуры и, так как ни одна из линий их не соединяет, то нарисовать её, не отрывая карандаш от бумаги, нельзя.
Нарисованные фигуры состоят из точек и соединяющих их линий. В информатике это является одной из возможностей представления объектов и связей между ними. Такие способы представления называются графами, которые состоят из вершин и соединяющий их рёбер.
Граф, в котором найдётся путь от любой вершины в любую другую (возможно с прохождением других вершин), называется связным. Граф можно нарисовать с помощью одной линии тогда и только тогда, когда он связный и в нём имеется ноль или две вершины, у которых есть нечётное число рёбер.
Проходящий каждое ребро графа только по одному разу путь называется эйлеровым (по имени знаменитого математика Леонарда Эйлера (1707-1783)). Он первым описал эту задачу на примере прогулки по семи мостам Кёнигсберга. В компьютере эйлеров путь находят с помощью алгоритмов Флёри (англ Fleury's algorithm) или Хиерхолцера (англ Hierholzer's algorithm).

Для урока географии Коля делает реферат. Он хочет добавить туда графики о населении в разных городах Эстонии. Коля размышляет над разными видами графиков, но в одном из них он допустил ошибку.
Какой из приведённых графиков НЕ ПРЕДСТАВЛЯЕТ те же данные, что и другие?
[Raadionupud]
A. 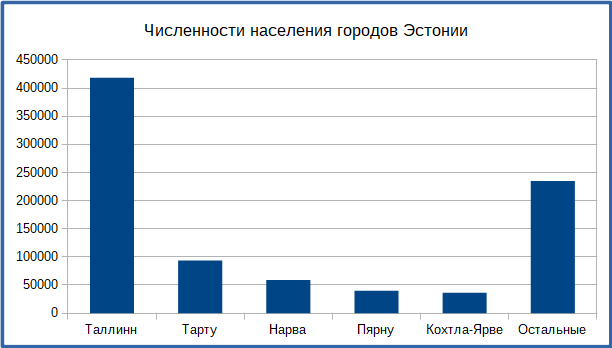 B.
B. 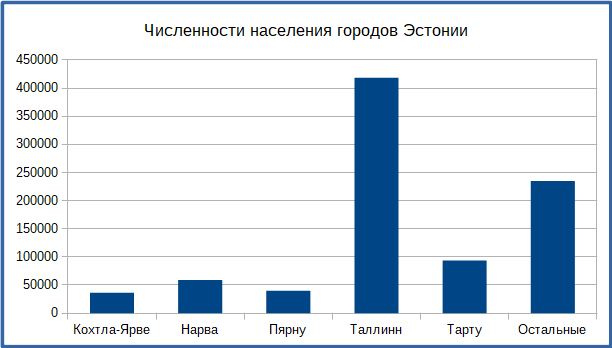
C. 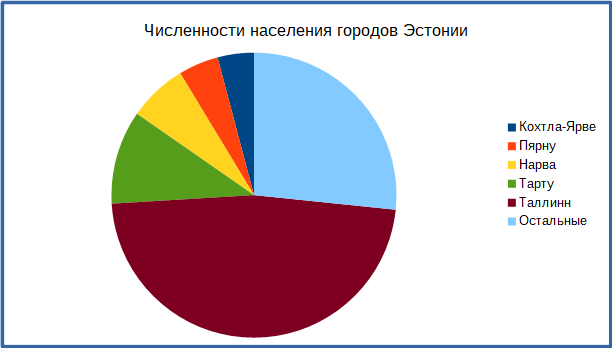 D.
D. 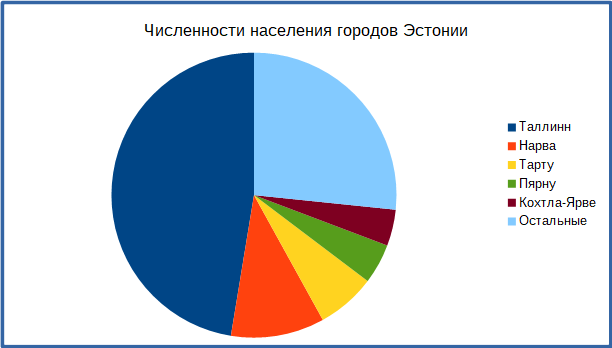
Правильный ответ: D.
На всех других графиках население Тарту больше населения Нарвы (что является фактологически верным моментом), а на графике D наоборот.
Часто одну и ту же информацию можно представить различными способами. Но даже если сами данные не содержат в себе ошибок, то некоторые формы представления данных лучше, чем другие. Например, на графике А, где данные упорядочены по численности населения, сразу видно, что Нарва является третьим по величине городом Эстонии. Однако, если упорядочить данные по названию городов (график В), понять это становиться сложнее.
Конечно, если с помощью графика хотят показать изменения какой-нибудь величины во временном промежутке, как, например, на приведённом ниже графике о населении Тарту в разные годы, то упорядочивание столбцов по их высоте является менее разумным выбором.
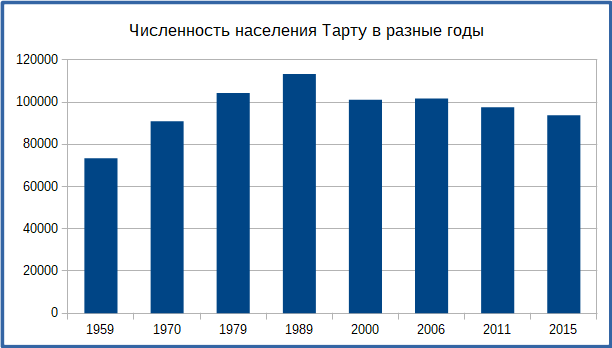
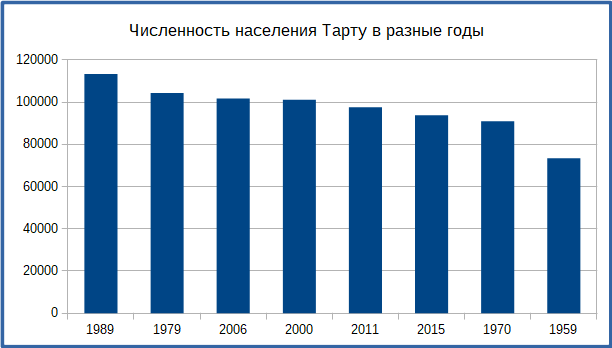
Данные, использованные в примерах, взяты из Википедии.

Летом младший брат Астрид прочитал книгу "Карлсон на крыше". На уроке эстонского языка его попросили написать краткое содержание книги.
В последний момент Астрид обнаружила, что во многих местах младший брат вместо "Karlsson" записал имя героя как "Karlson". К тому же в работе имя Карлсона используется в разных падежах. Даже получилось так, что местами имя героя записано верно, а местами с ошибкой.
Как Астрид может помочь брату быстро и с меньшими затратами исправить ошибку?
[Raadionupud]
A. Воспользуется возможностью текстового редактора заменить все встречающиеся в тексте "so" на "sso"
B. Воспользуется возможностью текстового редактора заменить все встречающиеся в тексте "Karlson" на "Karlsson"
C. С помощью функции "Поиск и замена" этого сделать за один раз не получится - придётся искать и заменять слово в каждом падеже отдельно
D. Из-за падежей эстонского языка нельзя вообще исправить ошибки с помощью функции "Поиск и замена" - текст придётся внимательно перечитать
Правильный ответ: B.
B является правильным ответом, так как при изменении слова "Karlson" по падежам основа слова не меняется. При замене слова "Karlson" на "Karlsson" происходят правильные замены: "Karlsoni" → "Karlssoni", "Karlsonit" → "Karlssonit" и так далее для остальных падежей.
A не является правильным ответом, так как в этом случае произойдёт замена уже правильно написанного слова "Karlsson" на неправильный вариант "Karlssson", а также, например, "Majasokk" → "Majassokk".
C вариант был бы верным, если необходимо было бы внести изменение в какое-нибудь слово, основа которого при изменении падежа также меняется. Например, если в разных падежах слова "õde" ("õde", "õe", "õele", ...) вместо буквы "õ" была бы случайно записана буква "ö". При изменении по падежам имя Карлсона так сильно не изменяется, и эту ошибку можно исправить более лёгким способом.
D вариант был бы верным, если неверно записанное нами слово могло бы быть в каком-нибудь другом контексте верным или его часть. Например, если бы в тексте было слово "öeldis" (рус сказуемое), то простая замена "öe" → "õe" сделала бы слово неверным. Во многих текстовых редакторах для решения таких спорных моментов при использовании функции "Поиск и замена" можно задать, что замене подлежат только слова целиком. Однако может случиться и так, что и такого решения будет недостаточно, и каждое такое сомнительное место придётся просмотреть отдельно.
Компьютеры бесспорно являются быстрыми и точными исполнителями команд, но при отдаче команды всегда необходимо помнить, что компьютер делает именно то, что ему приказали, даже если это не то, что хотел пользователь. Суть большей части информатики, и особенно программирования, заключается в том, чтобы придумать, как сформулировать свои желания наиболее точным способом.

Для урока биологии бобр Витя пишет реферат о птицах и животных. Содержание реферата он не стал писать вручную, а воспользовался возможностью его генерирования с помощью текстового редактора.
Для этого заголовки глав о млекопитающих и птицах он обозначил стилем Заголовок 1 (англ Heading 1). Заголовки разделов, где рассмотриваются млекопитающие (лиса, волк, заяц, бобр), он обозначил стилем Заголовок 2 (англ Heading 2). В разделе о бобрах есть два подраздела, которые также должны быть видны в содержании.

Сегодня Витя добавил в реферат в раздел о зайцах подразделы о белом, сером и американском зайцах.
Как следует оформить эти заголовки, чтобы они правильно отобразились в содержании?
[Raadionupud]
A. Их следует обозначить стилем Заголовок 1
B. Их следует обозначить стилем Заголовок 2
C. Их следует обозначить стилем Заголовок 3
D. Их следует обозначить стилем Заголовок 4
Правильный ответ: C.
Номер в стиле заголовка соответствует его уровню в структуре документа. Главы, как части с самым высоким уровнем, имеют номер 1; внутри них находящиеся разделы имеют номер 2; в свою очередь находящиеся в них подразделы имеют номер 3. Если бы в подразделах в свою очередь были бы озаглавленные абзацы, то номер их уровня был бы 4.
На сегодняшний день компьютеры ещё слабы для обработки данных в свободной форме. Зачастую для достижения желаемого результата пользователям приходится самим добавлять к данным обозначения того, как их следует обработать. Несмотря на то, что это может вначале показаться бессмысленной работой, на самом деле в перспективе это позволяет сэкономить время и силы.
Например, если заголовки отмечены стилями, то всё их оформление можно изменить за один раз. Для этого будет достаточно дать команду для переоформления заголовка с одним или другим стилем. Если бы заголовки не были бы отмечены стилями, то автору документа пришлось бы стиль каждого заголовка менять отдельно. Во-первых, это много работы, а, во-вторых, с этим сопряжён риск, что какой-нибудь заголовок будет пропущен, и в итоге документ будут оформлен различными стилями.

У бобра Коли имеется бесконечное множество кусочков пазла. Кусочки имеются двенадцати разных форм и трёх разных цветов:
| Цвет | Кусочки |
|---|---|
| КРАСНЫЙ |  |
| ЖЁЛТЫЙ |  |
| СИНИЙ |  |
Используя эти кусочки, он может создать разноцветные последовательности, например:
СИНИЙ → ЖЁЛТЫЙ → ЖЁЛТЫЙ → КРАСНЫЙ → ЖЁЛТЫЙ → СИНИЙ → ЖЁЛТЫЙ → ЖЁЛТЫЙ

Каждая последовательность должна начинаться с начального кусочка (кусочка, у которого левая сторона прямая) и заканчиваться конечным кусочком (кусочком, у которого правая сторона прямая). При составлении последовательностей Коля не может положить рядом друг с другом кусочки с прямыми краями.
Какую из приведённых последовательностей НЕЛЬЗЯ сконструировать из имеющихся у Коли кусочков пазла?
[Raadionupud]
ЖЁЛТЫЙ → СИНИЙ → СИНИЙ → КРАСНЫЙ → КРАСНЫЙ → КРАСНЫЙ → СИНИЙ
СИНИЙ → ЖЁЛТЫЙ → КРАСНЫЙ → ЖЁЛТЫЙ → КРАСНЫЙ
КРАСНЫЙ → КРАСНЫЙ → ЖЁЛТЫЙ → СИНИЙ → СИНИЙ → СИНИЙ
СИНИЙ → КРАСНЫЙ → ЖЁЛТЫЙ → СИНИЙ → КРАСНЫЙ → ЖЁЛТЫЙ → КРАСНЫЙ
Правильный ответ: C.
Коля не сможет соединить ни один синий кусочек с конечным кусочком синего цвета, и поэтому последовательность C он не сможет сконструировать.
В этом задании необходимо выложить кусочки пазла в определённом порядке. Некоторые комбинации подходят, а некоторые нет. Также и в информатике: если комбинируются различные элементы, то действуют правила, какие комбинации разрешены, а какие нет.
В данном задании правила даны в виде кусочков, хотя зачастую бывает очень трудно решить, соответствует ли последовательность правилам или нет: например, находятся ли выходные данные работы какой-нибудь части программы в таком виде, которым может воспользоваться следующая часть. В основном программы довольно негибкие и сообщают о некорректных входных данный, хотя иной раз по возможности пытаются разобраться в неверном виде поступивших входных данных. Хорошим примером могут служить, например, веб-браузеры, где предполагается, что пользователь хочет получить информацию даже тогда, когда на веб-страничке присутствуют технические ошибки.

Митя хочет опубликовать на сайте школы диаграммы результатов опроса учеников. Графический редактор позволяет сохранять изображения в различных форматах.
Какой из следующих форматов следует использовать для диаграмм?
[Raadionupud]
A. Windows Bitmap (*.bmp)
B. Encapsulated PostScript (*.eps)
C. Joint Picture Experts Group image format (*.jpg)
D. Portable Network Graphics (*.png)
Правильный ответ: D (PNG).
Для публикации диаграммы в Интернете из предложенных вариантов лучше всего подходит формат PNG. Это формат растровой графики, где каждая картинка представлена в виде маленьких разноцветных квадратиков. PNG формат основывается на сжатии без потерь. Это означает, что при восстановлении получим точно такие же первоначальные данные. Данный формат очень подходит для представления "искусственных" рисунков, состоящих из больших участков с однородным цветом или повторяющимся узором, или имеющих контрастные линии. Именно так и выглядят диаграммы. Также PNG формат поддерживается всеми современными браузерами, которые доступны в операционных системах для настольных компьютеров, планшетов и телефонов.
JPEG также является растровым форматом, но сжатие происходит с потерями. JPEG был создан для того, чтобы представлять "естественные" рисунки, как, например, фотографии, где много различных тонов и плавных переходов между ними. Если для сохранения рисунков с контрастными чёткими линиями использовать этот формат, то применяемый алгоритм сжатия приведёт к довольно большим искажениям (это видно на приведённом ниже сравнении). По этой причине этот формат не очень подходит для "искусственных" рисунков (графиков, чертежей, скриншотов).
BMP является растровым форматом без потерь, как и PNG, но основывается на более простых алгоритмах сжатия и поэтому сохранённые в этом формате файлы имеют больший размер, чем при сохранении точно такого же рисунка в формате PNG. Например, размер файла с одной примерно 600х350 пиксельной столбчатой диаграммой в формате PNG будет около 8 KB, а в формате BMP более 600 KB. Стоит учитывать, что BMP является форматом, специфичным для Windows, и поэтому не обязательно будет поддержан в браузерах других операционных систем.
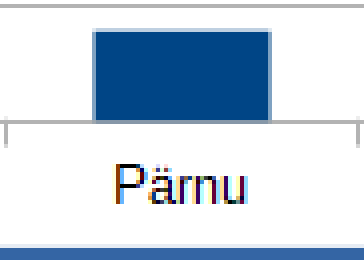
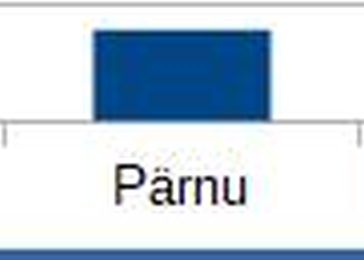
EPS отличается от всех вышеописанных форматов, потому что это формат векторной графики. Это означает, что имеющиеся в EPS-файле рисунки описываются не с помощью мозаики из пикселей квадратной формы, а с помощью объектов, состоящих из геометрических фигур (линий, прямоугольников, кругов и др.). Благодаря этому рисунки в векторном формате можно увеличивать и уменьшать без изменения качества. В приведённой ниже сравнительной таблице видно, что при увеличении представленных в формате PNG и BMP рисунков они становятся квадратоподобными, а в случае JPEG формата рисунок становится нечётким. В то же время рисунок в векторном формате остаётся чётким. Недостатком EPS формата является то, что он исторически был очень сложным форматом, применявшимся в типографии, и сейчас не поддерживается браузерами (для просмотра рисунков в этом формате необходима отдельная программа).
Scalable Vector Graphics (*.svg) является современным форматом векторной графики и предназначен для использования в Интернете. У этого формата в общем схожие с EPS форматом позитивные свойства и, если программное обеспечения для создания диаграмм поддерживает этот формат, предпочтительнее использовать именно его. Однако стоит иметь ввиду, что это довольно новый и находящийся ещё в процессе развития файловый формат, поэтому в случае некоторых сложных рисунков может получиться так, что все браузеры не смогут их достоверно отобразить.
| PNG/BMP (увеличение) | JPEG (увеличение) | SVG/EPS (увеличение) |
|---|---|---|
 |
 |
 |
Если одни и те же данные можно представить в разных форматах, как это, например, и есть в случае графики, то при выборе правильного формата надо знать его позитивные и негативные стороны.
Copyright © 2020 Bebras – International Challenge on Informatics and Computational Thinking.
Licensed under Creative Commons Attribution-ShareAlike 4.0 International License.
Flag icons by GoSquared.