Robotkäsi võtab komponente kolmelt konveierlindilt (A, B ja C) ning asetab neid koosteliinile. Täpsemalt töötab robotkäsi niimoodi:
Kui konveierlindil komponente enam pole, ootab robot, kuni neid sellele juurde saadetakse, sest koosteliin vajab komponente vaheldumisi kõigilt konveierlintidelt.
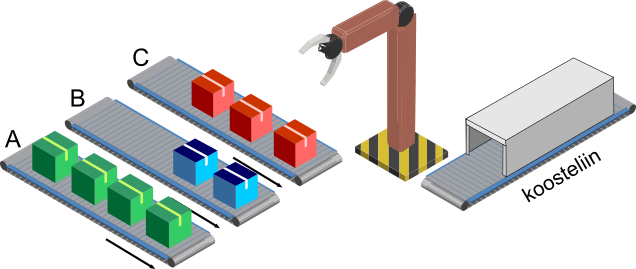
Mitu komponenti robotkäsi enne peatumist koosteliinile paneb, kui lähtuda joonisel olevast olukorrast ja teadmisest, et uusi komponente konveierlintidele ei lisandu?
[Täisarv [0, 12]]
Õige vastus on: 7.
Robotkäsi saab ilma takistusteta võtta komponente lintidelt A, B ja C järjest kaks ringi ja panna sellega koostelindile 6 komponenti. Kolmanda ringi ajal on lindil A veel komponent olemas, seega lisandub koosteliinile ka seitsmes komponent, kuid lindil B komponente enam pole ja robot jääb ootama.
Roboti töö on tihedalt seotud ajastamisega: kuidas korraldada tegevust nii, et töö saaks korralikult tehtud. Robotisse on programmeeritud teatud operatsioonide järjekord ja otsuste tegemise algoritm. Samuti on seal olemas veahaldusega tegelev osa selleks puhuks, kui midagi läheb valesti. Käesoleval juhul jälgitakse, kas järjekordsel konveierlindil on üldse komponente, mida koostelindile tõsta.
Robottolmuimeja 
liigub seintega ümbritsetud ruumis, mis on jagatud 6x7 ruudukujuliseks alaks.
Robot asub alati mõne ruudu keskel suunaga mõne seina poole. Robotit saab liigutada programmi abil, mis koosneb järgmistest käskudest:
EDASI: liigu järgmisesse ruutu enda ees:
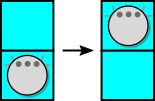
PAREMALE: pööra 90 kraadi paremale ehk kellaosuti liikumise suunas, kuid jää samasse ruutu:
VASAKULE: pööra 90 kraadi vasakule ehk vastu kellaosuti liikumise suunda, kuid jää samasse ruutu:
Kujutame ette, et robotis on järgmine programm:
EDASI VASAKULE EDASI PAREMALE EDASI
Nimetame ruutu ohutuks, kui sellelt ruudult alustav robot saab programmi alati täita vastu seina põrkamata, sõltumata roboti suunast algasendis.
Mitu ohutut ruutu ruumis on?
[Täisarv [0, 42]]
Õige vastus on: 6.
Programmi täitmise ajal liigub robot kokkuvõttes 2 ruutu edasi ja ühe ruudu vasakule:
Peab silmas pidama, et see oleks võimalik igas neljas suunas. Kui robot alustab mõnest seina ääres olevast ruudust (nn. ääreruudust) või mõnest ääreruudu naaberruudust, siis on vähemalt üks suund, kuhu programmi järgi liikudes kohtub robot seinaga. Alloleval joonisel on ohutud ruudud märgitud tumedamas toonis.
Programmi kirjutades peavad programmeerijad mõtlema kõikvõimalikele situatsioonidele, mis programmi töötamise ajal ette võivad tulla. Nad peavad keskenduma olukordadele, mis võivad viia avariideni või vale käitumiseni, seega peavad nad kontrollima ja määratlema programmi tööks vajalikud algsed tingimused ja programmi testima.
Meie robot töötab samal viisil nagu vana tuntud kangelane, mis loodi lastele ühes esimestest programmeerimiskeeltest. Selle roboti nimi oli Karel ja see ilmus arvutitesse rohkem kui 40 aastat tagasi. Nimi on pandud tšehhi kirjaniku Karel Čapeki järgi, kes kasutas esimesena intelligentsete mehaaniliste töötajate kohta sõna "robot" oma näidendis R.U.R. 1920. aastal ehk juba sada aastat tagasi. Tema futuristlik draama kirjeldas tehast, kus toodeti inimeste asemel ja inimeste heaks töötavaid roboteid, et luua maapealne paradiis. Kuid midagi ei kesta igavesti ja isegi robotid võivad hakata oma peaga mõtlema...
Üks arvutitest (joonisel vasakul üleval) nakatus "uinuva viirusega". Viirus aktiveerub alles kolm päeva pärast nakatumist ja nakatab siis kõik teised selle arvutiga vahetult ühendatud arvutid. Ka igas uues nakatunud arvutis ootab viirus enne aktiveerumist 3 päeva. Arvutite omavahelised ühendused arvutivõrgus on toodud joonisel. Kui arvuti on juba nakatunud, siis see enam uuesti ei nakatu.
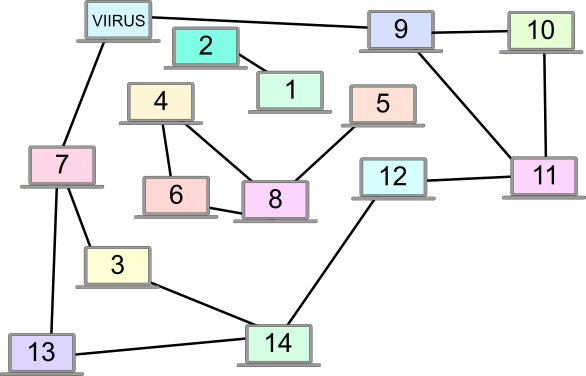
Mitme päeva järel saame öelda, et selles koldes rohkem arvuteid enam ei nakatu?
[Täisarv]
Õige vastus on: 9.
Et päevade arvu teada saada, alustame viirust kandva arvuti naabritest: kolme päeva pärast nakatuvad arvutid 7 ja 9.
Kuue päeva pärast saavad ohvriteks arvutid 3, 13, 10 ja 11.
Üheksa päeva pärast nakatuvad lõpuks ka viimased samas võrgus olevad arvutid 12 ja 14.
Arvutid 1, 2, 4, 5, 6 ja 8 pole nakatunutega ühendatud ja jäävad puutumata.
Graaf koosneb tippudest (mis tähistavad meie ülesandes arvuteid) ja neid ühendavatest servadest (ühendused arvutite vahel). Sidususkomponendiks nimetatakse omavahel servadega ühendatud tippude hulka (meie ülesandes on iga sidususkomponent eraldi arvutivõrk). Kuna viirus liigub arvutist arvutisse võrguühendusi pidi, nakatuvad ainult samas võrgus olevad arvutid.
Graafi sidususkomponenti kuuluvaid tippe võib läbida mitmel erineval viisil. Selles ülesandes kirjeldatud viisi, kus viirus levib igast nakatunud arvutist kõigisse selle naabritesse, nimetatakse üleujutamise (ingl flood fill) algoritmiks. Nimi tuleb sellest, et viiruse levimine meenutab maha valatud vedeliku laialivoolamist kõigis suundades. Sama algoritmi kasutatakse näiteks arvutigraafikas alade värvi või tekstuuriga täitmiseks.
Koprad mängivad mängu, mille nimi on "Ruudud", ja nad kõik soovivad sellest osa võtta. Mängu kohaks on park, mis on jagatud ruutudeks. Pargis on ka maja ja puud, nendesse ruutudesse koprad minna ei tohi, seega on tühje ruute 26.
Mängu alguses läheb iga mängija ühte tühja ruutu ja edasi püüavad nad liikuda nii, et iga mängija külastaks mängu jooksul kõiki 26 tühja ruutu. Korraga ei tohi üheski ruudus olla rohkem kui üks kobras, samuti ei tohi liikuda mööda diagonaale.
Näiteks võivad koprad liikuda sel viisil:
Milline on maksimaalne arv kopraid, kes saavad pargis seda mängu mängida? Paneme tähele, et igal kopral peab olema võimalik liikuda kõigisse 26 tühja ruutu.
[Raadionupud]
A. 13
B. 23
C. 25
D. 26
Õige vastus on: B (23).
Ülesanne on sarnane nn 15-nupu mängule, kus on 4x4 mängulaual on 15 nummerdatud nuppu ning mängija eesmärk on nupud ühe sammu haaval õigetesse kohtadesse liigutada. Takistusteta mängulaual piisab ühest tühjast ruudust, et oleks võimalik iga nuppu igasse ruutu viia.
Meie ülesandes on aga paremal ülanurgas maja taga kaks ruutu, kuhu sattunud koprad jäävad lõksu ega saa enam liikuda:
Ka kahe tühja ruudu puhul tekib olukord, kus üks kobras saab liikuda vaid kolme ülemise parempoolse ruudu vahel:
Seega ei saa seda mängu mängida 24 (või rohkema) kopraga.
Küll aga näeme allolevalt jooniselt, et kolme tühja ruudu jätmisel saavad kõik koprad ka kaht maja taga asuvat ruutu külastada:
Seega ongi õige vastus 26-3=23.
Ülesande lahendamine nõuab analüütilist mõtlemist. Peale ülevaate saamist tuleb keskenduda erijuhtudele (nn piirsituatsioonidele), et uurida, kas nende tõttu peab algset üldist lahendust muutma. Selline oskus on eriti oluline tarkvara testimisel. Antud juhul on kaks parempoolset ülemist ruutu erijuhuks, mida peab erilise tähelepanuga analüüsima.
Viiruse leviku tõttu peab vallas sulgema mõned toidupoed, aga igal juhul tuleb iga küla lähedusse jätta vähemalt üks pood. Ütleme, et pood on küla lähedal, kui ükski teine küla ei jää poodi minnes tee peale.
Rohelised täpid tähistavad külasid, punased ruudud toidupoode, jooned nende vahel aga teid.
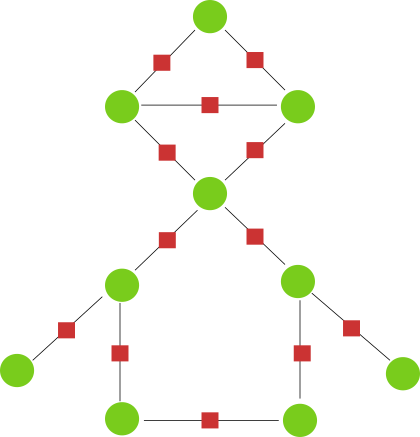
Milline on minimaalne alles jäävate toidupoodide arv, et iga küla lähedale jääks siiski pood?
[Täisarv [0, 12]]
Õige vastus on: 5.
Kindlasti peavad alles jääma kõige vasakpoolsem ja kõige parempoolsem toidupood, et varustada äärmisi külasid. Kaardi allääres olevate külade varustamiseks piisab kõige alumisest toidupoest. Nende kolme poe abil on toiduainetega varustatud kõik kuus alumisel kaardipoolel olevat küla. Ülemise nelja küla varustamiseks peame säilitama veel vähemalt kaks poodi, sest mitte mingi üks pood ei ole nende kõigi läheduses. Nendeks kaheks sobivad ülemise ruudu vastaskülgedel olevad poed.
Ülesandes on eesmärgiks jätta graafis alles võimalikult väike arv servi nii, et kõik tipud oleksid seotud mõne servaga. Antud juhul on tippudeks külad ja servadeks teed koos toidupoodidega. See on informaatikas tuntud graafi servakatte (ingl edge cover) leidmise ülesandena ja selle lahendamise ideed on omakorda kasutusel paljudes teistes algoritmides näiteks toesepuude (ingl spanning tree) või lühimate teede otsimiseks.
Koprad lõid paroolide komplekti, et kaitsta oma maju. Paroolid koosnevad vaid kahest sümbolist: 
ja 
.
Paroolikontrollija peab otsustama, kas parool on õige või vale, selle tööd illustreerib joonis:
Eeltoodud näites loetakse õigeks parooliks vaid sellist:
Koprad lõid uue paroolikontrollija:
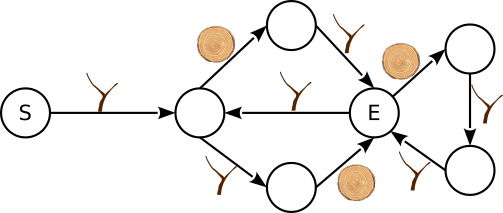
Millised alltoodud paroolidest loeb uus paroolikontrollija õigeteks?
[Märkeruudud]
A. 
B. 
C. 
D. 
E. 
Õige vastus on: A ja B.
Õiged on paroolid A ja B, kuna nende läbimisel satutakse ringi E.
Parool C on vale, sest esimene sümbol on , kuid kõik sobivad paroolid peavad algama sümboliga .
Parool D on vale, sest see koosneb kümnest sümbolist, kuid kõikide sobivate paroolide pikkused peavad jaguma kolmega; kontroll peatub enne üheksandat sümbolit.
Parool E on vale, sest sümbol esineb selles 5 korda ja sümbol 4 korda, kuid sobivad paroolid koosnevad kahe kolmandiku ulatuses sümbolitest ja ühe kolmandiku ulatuses sümbolitest ; kontroll peatub enne viimast sümbolit.
Kobraste paroolikontroll on ülesehitatud nn. olekumasinana (täpsemalt lõpliku determineeritud automaadina). See on matemaatiline mudel. Selline masin saab olla igal ajamomendil ainult ühes toodud olekutest, olekut muudab sisendist tulev info.
Olekumasinaid kasutatakse tegevuste järjekorra kontrollimisel erinevate seadmete juures, näiteks müügiautomaadid (ostuprotsessi erinevad sammud), liftid (peatuste järjekord vastavalt kasutajate soovidele), valgusfoorid (režiimi muutmine, kui auto on ootel), koodlukud (sisestatud numbrijärjendi kontroll) jne.
Alltoodud linnaplaanil on näha palju ühesuunalisi tänavaid, mida tähistavad ühe otsaga nooled, kuid mõned tänavad on ka kahesuunalised.
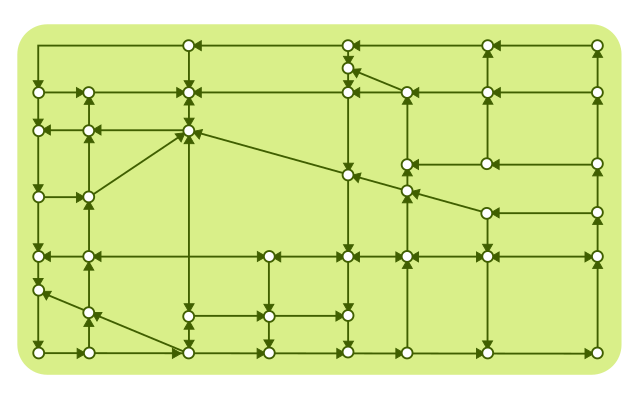
Ristmikku, kuhu saab liikuda vaid ühelt ristmikult, nimetatakse haavatavaks.
Kui palju on linnaplaanil haavatavaid ristmikke?
[Täisarv [0, 44]]
Õige vastus on: 14.
Haavatavaid ristmikke on 14:
Selliseid struktuure kutsutakse võrkudeks. Võrk on suunatud graaf ja igasse tippu suunatud noolte arvu nimetatakse selle tipu sisendastmeks. Tipp on haavatav, kui selle sisendaste on 1, ja juurdepääsmatu, kui sisendaste on 0.
Rünnak võrgu haavatavate punktide vastu tekitab probleeme näiteks ligipääsuga olulistele teenustele. Võrgu analüüs ja haavatavate kohtade leidmine on tähtis töö võrgu disainimisel, et vähendada informatsiooni kadu.
Kopra-Toomasel on 9 kuuli ja karp 9 lahtriga:
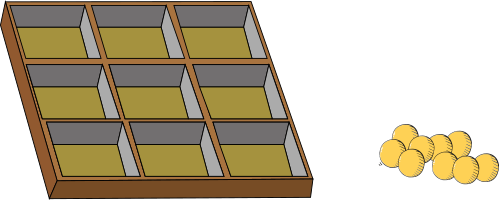
Ta valib mingi arvu kuule vahemikus 0 kuni 9 ja paigutab need karpi vastavalt järgmistele reeglitele:
Kui mitmel viisil saab Toomas kuule karpi panna?
[Raadionupud]
A. 12
B. 16
C. 64
D. 512
Õige vastus on: B (16).
Alustame 2x2 lahtri suurusest alast karbis:
Meil on 4 lahtrit ja igas lahtris võib kuul olla või mitte olla. Seega on 2^4 = 16 erinevat viisi kuule sellesse alasse panna.
Tähtis on märgata, et kui Toomas on need neli lahtrit mingil viisil täitnud, pole tal enam valikut ülejäänud lahtrite puhul: kuna reeglites on kirjas, et igas reas ja veerus peab olema paarisarv kuule, siis see, kuidas on algses 2x2 alal kuule paigutatud, määrab ära, kuidas ülejäänud lahtritesse kuule pannakse.
Näiteks oletame, et Toomas pani kuulid 2x2 alale selliselt:
Kuna esimeses veerus on vaid üks kuul, siis peab Toomas panema kuuli lahtrisse A, et veerus olevate kuulide arv oleks paarisarv. Teises veerus on juba paarisarv kuule olemas, seega peab lahter B jääma tühjaks. Nii jätkates saame aru, et Toomas peab jätma tühjaks ka lahtri C ning panema kuulid lahtritesse D ja E.
Kuna variante 2x2 ala täitmisel oli 16 ning ülejäänud lahtrite täitmisel rohkem valikuvõimalusi polnud, on kogu karbi kuulidega täitmisel samuti vaid 16 võimalust.
Andmete säilitamine ja transport on informaatikas oluline teema. Üks võimalus kontrollimiseks, et andmetega pole transpordi käigus midagi juhtunud, on paarsuskontroll. Paarsusbitt väärtusega 0 või 1 arvutatakse välja vastavalt eelnevatele andmetele (et saada kokku vastavalt kokkuleppele kas paarisarv või paaritu arv 1-bitte) ja lisatakse andmete lõppu. Pärast transporti arvutatakse andmete põhjal taas välja paarsusbitt ja kontrollitakse, kas tulemus on samasugune. Kui saadud paarsusbiti väärtus erineb algsest, on andmetega midagi juhtunud.
Antud ülesandes ongi lahtrid viimases reas ja viimases veerus paarsusbittideks. Kui selline karp oleks saadetud edasi, võiks saaja kontrollida ridade ja veergude summasid ning kui need poleks olnud paarisarvud, saaks ta Toomasele veast teada anda.
Koprad numbritega 1 kuni 6 istuvad kuues kõrvuti asetsevas tugitoolis ja tahavad mängida mängu. Enne mängu valitakse üks arv ühest neljani. Iga plaksu järel peavad koprad minema nii mitu tooli paremale, nagu on valitud arv, rivi lõppu sattunud koprad peavad aga tulema rivi algusesse. Pärast liikumist läheb kõige parempoolsem kobras mängust välja ja ka viimane tool eemaldatakse. Viimasena alles jäänud kobras on mängu võitnud.
Näiteks, kui valida arv 2, siis võidab kobras number 6:
Millise numbriga kobras tuleb võitjaks, kui valitakse arv 3?
[Täisarv [1, 6]]
Õige vastus on: 2.
Programmeerimises kasutatakse sageli bittide tasemel operatsioone nii arvude võrdlemisel kui arvutamisel. Sellised operatsioonid on kiired ja lihtsad ning neid toetatakse otseselt protsessori tasemel. Üks bitioperatsioonide vorme on ringnihe, mille puhul võime ette kujutada, et bitijada otsad on omavahel ühendatud: biti nihutamine rea ühest otsast välja viib selle hoopis teise otsa algusesse. Selline võte on kasulik, kui vaja on alles hoida kõiki bitte. Seda kasutatakse tihti näiteks krüptograafias.
Ringnihe vasakule (MSB - most significant bit, suurima kaaluga bitikoht; LSB - least significant bit, vähima kaaluga bitikoht):
Ringnihe paremale:
Kobras Kaupo paneb ritta kaheksat erinevat tüüpi plaate, millel on igaühel kindel väärtus:
Nende ritta seadmisel peab ta arvestama teatud reeglitega:
Näiteks kolmandal kohal peab olema plaat väärtusega 3, sest esimesel kohal oleva plaadi väärtus 1 ja teisel kohal oleva plaadi väärtus 2 annavad liites kokku arvu 3:
Millise plaadi paneb Kaupo selles reas 8. kohale?
[Raadionupud]
A. 
B. 
C. 
D. 
Õige vastus on: C.
Selgitus on toodud joonisel, kus lisamist on näidatud alates 4. plaadist:
Reegel, mida selles ülesandes kasutatakse, seob järgmise plaadi valiku eelmiste plaatidega. Tegemist on rekursiivse algoritmiga: ta "kasutab iseennast". Matemaatikast on tuntud näiteks Fibonacci arvude defineerimine samal viisil: iga järgmine arv on kahe eelmise summa. Sarnast jada näeme me üllatavalt sageli ka looduses: okste lisandumine puule, taimede paljunemine jne.
Erinevalt klassikalisest Fibonacci jadast pole meie ülesandes tegemist lõpmatult kasvavate väärtustega, sest meil on lisareegel, mis asendab teatud piirist suuremad summad väärtusega -2.
Informaatikas on rekursioon laialdaselt kasutatav tehnika, kui lahendatavat ülesannet saab jagada väiksemateks osadeks, mis on oma loomult sarnased algsele, kuid lihtsamad lahendada.
Tabelarvutussüsteemis tähistatakse esimest 26 veergu ladina (täpsemalt küll inglise) tähestiku tähtedega:
Järgmist 26 veergu tähistatakse 2-täheliste kombinatsioonidega AA kuni AZ:
Nende järel järgmist 26 kombinatsioonidega BA kuni BZ:
Nii jätkub see, kuni kahetähelised kombinatsioonid ZZ järel otsa saavad. Siis alustatakse kolmetähelistega AAA kuni AAZ:
Milline on 2020. veeru tähis?
[Raadionupud]
A. BXR
B. BYR
C. CXR
D. CYR
Õige vastus on: B (BYR).
Üks võimalus vastuse leidmiseks on avada tabelarvutusprogramm, panna kursor töölehe esimesse veergu, vajutada 2019 korda klahvi "nool paremale" ja vaadata siis vastava veeru tähis. See on muidugi tüütu ja lisaks on üsna suur risk, et vahepeal võib loendamine segi minna.
Teine võimalus on arvutada igale pakutud variandile vastav veerunumber. Selleks paneme tähele, et
ühetäheliste tähistega on 26 veergu, ehk veerud 1 kuni 26;
kahetähelistes tähistes on võimalikke esitähti 26 ja iga esitähe järele teiseks täheks ka 26 võimalikku varianti; seega on kahetähelisi tähiseid kokku 26*26=676; seega on kahetäheliste tähistega veerud 27 kuni 702;
A-tähega algavates kolmetähelistes tähistes on teise ja kolmanda tähena kõikvõimalikud kahetähelised paarid, mida eelmise punkti põhjal on 676; seega on A-tähega algavate kolmetäheliste tähistega veerud 703 kuni 1378;
B-tähega algavate hulgas on BXR ees veel 23*26+17=615 veergu: kõigepealt sellised, kus teine täht on A kuni W (23 võimalust) ja iga teise tähe jaoks käivad kolmandana läbi A kuni Z (26 võimalust), ning siis veel sellised, mille alguses on BX ja kolmanda tähena esinevad A kuni Q (17 võimalust); seega on BXR ees veel veerud 1379 kuni 1993 ja BXR enda number on 1994;
eelmise punktiga sarnaselt aruvutades saame, et BYR ees on veel 24*26+17=641 B-tähega algavat kolmetähelist tähist ja seega BYR number ongi otsitav 2020;
ülesande lahendamiseks pole see enam vajalik, aga samamoodi saame leida ka, et CXR veeru number on 2670 ja CYR oma 2696.
Arvutisüsteemides on alatasa vaja mitmesuguste objektide tähiseid erinevate esituste vahel teisendada. Kõike tavalisem näide on arvude teisendamine inimestele harjumuspärase kümnendsüsteemi ja arvutis sisemiselt kasutatava kahendsüsteemi vahel.
Näiteks kui me kirjutame 10-süsteemis 345, siis tähendab see avaldist
310^2 + 410^1 + 5*10^0 = 300+40+5 = 345.
Sama arvu esitus 2-süsteemis oleks 101011001, mis tähendab avaldist
12^8 + 02^7 + 12^6 + 02^5 + 12^4 + 12^3 + 02^3 + 02^1 + 1*2^0 = 256+64+16+8+1 = 345.
Tabeliveergude tähistes on kasutusel 26 "numbrit" A kuni Z, ja nii on meil tegemist 26-süsteemiga, kus iga järgmise järgu kaal on eelmise omast 26 korda suurem. Aga erinevalt klassikalisest positsioonilisest süsteemist, kus 26 numbri väärtused peaks olema 0 kuni 25, on tabeliveergude tähistamisel nende väärtusteks 1 kuni 26.
Seda tausta teades saaksime vastuse selgitusena toodud sammukaupa arutelu asemel arvutada otse (kasutades tähtede väärtuste spikrina esimest ülesande tekstis olevat joonist):
BXR = 226^2 + 2426^1 + 1826^0 = 1352 + 624 + 18 = 1994, BYR = 226^2 + 2526^1 + 1826^0 = 1352 + 650 + 18 = 2020, CXR = 326^2 + 2426^1 + 1826^0 = 2028 + 624 + 18 = 2670, CYR = 326^2 + 2526^1 + 1826^0 = 2028 + 650 + 18 = 2696.
Kitsas parklas võivad autod teha järgmisi manöövreid:
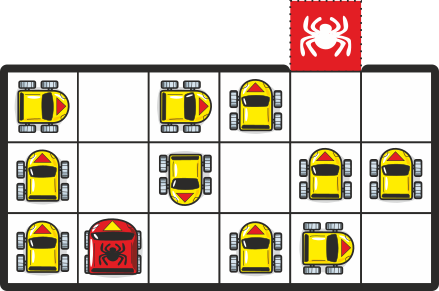
Selleks, et punane auto pääseks parklast välja, on vaja manööverdada ka teiste autodega.
Milline on vähim kõigi autode manöövrite koguarv, et punane auto jõuaks punasele ruudule?
[Raadionupud]
9
11
13
15
Õige vastus on: B (11).
Punane auto saab parklast välja järgmise 11 manöövriga:
Nüüd on lisaks vaja veenduda, et 11 on tõesti vähim võimalik manöövrite arv.
Selleks kujutame esmalt ette, et punane auto on ainuke auto parklas. Siis peaks ta parklast välja saamiseks liikuma kokku 2 ruutu põhja suunas ja 3 ruutu ida suunas ja pöörama 2 korda. Ta võib teha neid manöövreid mitmes erinevas järjekorras, aga igal juhul tuleb tal teha vähemalt need 8 manöövrit.
Kuna parklas on ka teisi autosid, tuleb punase auto läbilaskmiseks neid ka liigutada.
Esmalt paneme tähele, et punase auto teed blokeerib allpool toodud L-kujuline kolmik. Nende vahele läbipääsu tekitamiseks piisab ühest manöövrist:
Edasi blokeerib punase auto teed järgmine L-kujuline kolmik. Nende vahele ühe manöövriga läbipääsu tekitada ei saa. Küll aga on see võimalik kahe manöövriga:
Seega ongi punase auto väljapääsemiseks vaja teha vähemalt 8+1+2 = 11 manöövrit.
See ülesanne kuulub optimeerimisülesannete hulka: meil on vaja ülesanne mitte lihtsalt lahendada, vaid teha seda mingi mõõdupuu järgi parimal võimalikul viisil. Sellistes ülesannetes on sageli kõige raskem osa just leitud lahenduse optimaalsuse tõestamine.
Paljudel juhtudel on ainus võimalus selleks kõigi variantide täielik läbivaatus (ingl exhaustive search): leiame kõik võimalikud lahendused ja näitame, et kõik teised on halvemad kui meie oma. Mõnelgi juhul võib kõigi variantide käsitsi kontrollimine olla liiga suur töö, aga arvutile jõukohane. Siiski on paljudes ülesannetes variantide arv nii suur, et nende kõigi kontrollimine võtaks ka arvutil liiga palju aega. Siis tuleb kasutada kas keerukamaid algoritme, nagu näiteks otsingupuu pügamist (ingl search tree pruning) või harude ja tõkete meetodit (ingl branch and bound) või iteratiivset süvendamist (ingl iterative deepening).
Mõnikord on aga võimalik leida ülesandes mingid erilised tingimused (nagu selles ülesandes L-kolmikud), mille abil võib lahenduse optimaalsust näidata ilma teisi variante läbi vaatamata. Mõnikord on need eritingimused ühe juhtumi spetsiifilised (näiteks kui kollased autod oleks paigutatud teisiti, ei tarvitseks L-kolmikute abil arutlemine sihile viia), mõnikord aga õnnestub leida üldised tingimused (nn invariandid), mis näitavad, et mingi ühe meetodi või süsteemi järgi koostatud lahendus on alati parim võimalik. Näiteks annab mõnes optimeerimisülesandes parima lahenduse nn ahne algoritm (ingl greedy algorithm), mis teeb igal sammul sel hetkel kõige kasulikumana tunduva käigu ilma mingit kaugemat strateegiat arvestamata.
Kirjamasin suudab tuvastada viit pilti, mis kujutavad endast tähti I, T, O, C ja L.
Kirjamasin kasutab tuvastamisel nn. soojuskaarte. Pildi soojuskaardil näitab iga piksli (punkti) värv pildi vastava piksli värvi unikaalsust teiste piltide hulgas: mida unikaalsem on pildi piksli värv, seda heledam on piksel soojuskaardil.
Unikaalne: ühelgi teisel pildil pole selles kohas sama värvi pikslit.
Pigem unikaalne: ainult ühel teistest piltidest on selles kohas sama värvi piksel.
Pole unikaalne: kahel teistest piltidest on selles kohas sama värvi piksel.
Pigem tavaline: kolmel teistest piltidest on selles kohas sama värvi piksel.
Tavaline: kõigil piltidel on selles kohas sama värvi piksel.
Näiteks pildi 
soojuskaart on 
.
Millise pildi soojuskaart on 
?
[Raadionupud]
A. 
B. 
C. 
D. 
Õige vastus on: B.
Küsitaval soojuskaardil on 2. rea 3. veerus valge piksel. See tähendab, et see piksel on ühel tähel kõigist teistest erinev.
on ainuke pilt, millel on selles asukohas teistest erinev, täpsemalt must piksel; kõigil teistel piltidel on see piksel valge.
Siin on toodud kõik tähed koos neile vastavate soojuskaartidega:
Soojuskaart (ingl heat map) on andmete graafilise kujutamise üks viisidest, kus arvväärtused on asendatud värvikoodiga. Me oleme näinud selliseid kaarte näiteks ilmateadetes, kus värvidega tähistatakse erinevate piirkondade temperatuuri või sademete hulka.
Samuti kasutatakse soojuskaarti sarnaselt sellele ülesandele pildituvastuses, juhtides näiteks tehisnärvivõrkude treenimisel tähelepanu just teatud aladele pildil.
Kopraatias kasutatakse arvude märkimiseks ainult nulle ja ühtesid. Kaks Kopraatia last otsisid oma emale sünnipäevakingitust. Selleks oli neil kahe peale raha 11000101 kobrut. Lapsed leidsid kolm võimalikku kingitust: salli hinnaga 1110110 kobrut, kaelakee hinnaga 11001000 kobrut ja kella hinnaga 10011101 kobrut.
Milline on kõige kallim kingitus, mille lapsed saavad olemasoleva raha eest osta?
[Raadionupud]
A. Sall
B. Kaelakee
C. Kell
Õige vastus on: C (kell).
Antud kingitustest maksab kaelakee rohkem, kui on lastel raha: 11001000 > 11000101. Ülejäänud kahe asja jaoks on neil piisavalt raha: 1110110 < 11000101 ja 10011101 < 11000101. Seega saavad nad osta kas salli või kella. Neist kahest on kallim kell: 1110110 < 10011101.
Ülesanne on seotud kahendsüsteemiga. Kahendsüsteem kasutab erinevalt meie jaoks harjumuspärasest kümnendsüsteemist arvude märkimiseks vaid kaht numbrit: 0 ja 1. Kasutusel on ka teised arvusüsteemid, näiteks kaheksandsüsteem (numbrid 0-7) ja kuueteistkümnendsüsteem (numbrid 0-9 ning neile lisaks tähed A, B, C, D, E ja F).
Arvutid kasutavad kahendsüsteemi selle lihtsuse tõttu. Me võime mõelda numbrist 0 kui signaali puudumisest (lüliti on olekus "väljas") ja numbrist 1 kui signaali olemasolust (lüliti on olekus "sees"). Sel viisil saame lülitite erinevate olekute järgnevusena esitada suvalisi arve. Ka muud andmed (näiteks tähed) teisendatakse kahendarvudeks ja nii võib jada 01101000 tähistada kas arvu 104 või tähte "h".
Mati tahab avaldada kooli veebilehel õpilaste küsitluse tulemuste tulpdiagrammid. Kujundustarkvara võimaldab salvestada pilte mitmes vormingus.
Millist allolevatest vormingutest peaks diagrammide jaoks kasutama?
[Raadionupud]
Õige vastus on: D (PNG).
Pakutud variantidest on diagrammide veebis esitamiseks sobivaim vorming PNG. See on rastergraafika vorming, mis tähendab, et iga pilt esitatakse väikeste erivärviliste ruudukestena. PNG vorming kasutab kadudeta pakkimist, mis tähendab, et lahtipakkimisel saame tagasi täpselt esialgsed andmed. See vorming on sobiv suurte ühtlast värvi või korduva mustriga pindade ja kontrastsete joontega "kunstlike" jooniste esitamiseks, nagu diagrammid ongi. Ka on PNG vorming toetatud kõigis tänapäevastes veebilehitsejates nii arvuti- kui ka tahvli- ja telefoniopsüsteemides.
JPEG on samuti rastervorming, kuid kasutab kadudega pakkimist. JPEG on loodud, et esitada "naturaalseid" pilte, näiteks fotosid, kus on palju erinevaid toone ja sujuvaid üleminekuid nende vahel. Kontrastsete teravate joontega piltidel põhjustab selles vormingus kasutatav pakkimisalgoritm üsna suuri moonutusi, nagu näha allolevas võrdluses. Sellepärast ei ole see vorming kuigi sobiv "kunstlike" piltide (graafikud, joonised, erkaanitõmmised) jaoks.
BMP on kadudeta rastervoming, nagu ka PNG, kuid kasutab palju lihtsamat pakkimisalgoritmi, mistõttu on selles vormingus failid palju suuremad kui saaksime sama pilti PNG vormingus salvestades. Näiteks ühe umbes 600x350 pikseli suuruse tulpdiagrammi faili maht PNG vormingus on umbes 8 KB, aga BMP vormingus üle 600 KB. Lisaks on BMP Windowsi-spetsiifiline vorming ja ei tarvitse kõigi opsüsteemide veebilehitsejates toetatud olla.
EPS on kõigist eelnevatest erinevat vektorgraafika vorming. See tähendab, et EPS-failis kirjeldatakse pilti mitte ruudukujulistest pikselitest mosaiigina, vaid joontest, ristkülikutest, ringidest jmt geomeetrilistest objektidest koosnevana. Tänu sellele saab vektorvormingus pilte suurendada ja vähendada ilma, et nende kvaliteet sellest muutuks. Allolevas võrdlustabelis on näha, et PNG ja BMP vormingus pildid muutuvad suurenamisel ruuduliseks ning JPEG vormingus pilt läheb uduseks, aga vektorvormingus pilt jääb endiselt teravaks. EPS vormingu puudus on, et see on ajalooliselt trükitööstuses kasutusel olnud väga keeruline vorming ja ei ole veebilehitsejates toetatud (selles vormingus piltide vaatamiseks on vaja lisaprogrammi).
Tänapäevane ja ka veebis kasutamiseks mõeldud vektorgraafika vorming on Scalable Vector Graphics (*.svg). Sellel on üldiselt EPS vorminguga sarnased positiivsed omadused ja kui diagrammide koostamise tarkvara seda vormingut toetab, on see enamasti parim valik. Siiski tasub silmas pidada, et see on üsna uus ja veel arenev failivorming ning mõnede keerulisemate jooniste puhul võib juhtuda, et kõik veebilehitsejad ei oska neid päris õigesti näidata.
| PNG/BMP (suurendus) | JPEG (suurendus) | SVG/EPS (suurendus) |
|---|---|---|
 |
 |
 |
Kui samu andmeid on võimalik esitada mitmes erinevas vormingus, nagu see näiteks graafika puhul on, siis peab õige vormingu valimiseks teadma iga vormingu tugevaid ja nõrku külgi.
Copyright © 2020 Bebras – International Challenge on Informatics and Computational Thinking.
Licensed under Creative Commons Attribution-ShareAlike 4.0 International License.
Flag icons by GoSquared.