Роботизированная рука берёт компоненты с трёх конвейерных линий (A, B и C) и кладёт их на сборочную линию. Известно, что рука работает следующим образом:
Если на конвейерной линии больше нет компонента, то роботизированная рука ждёт, пока он не появится вновь на линии, так как сборочная линия нуждается в поступающих поочерёдно с каждой конвейерной линии компонентах.
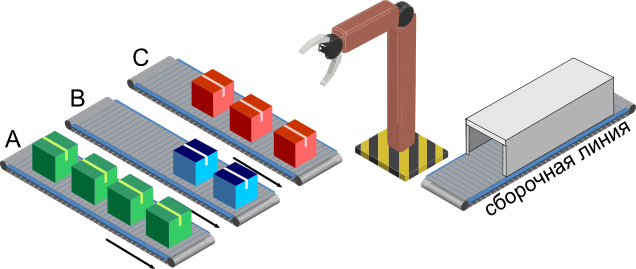
Сколько компонентов до остановки успеет роботизированная рука положить на сборочную линию, если исходить из приведённого на рисунке положения дел и учитывать, что новых компонентов на конвейерные линии больше не добавится?
[Täisarv [0, 12]]
Правильный ответ: 7.
Роботизированная рука сможет без проблем два круга подряд брать компоненты с линий A, B и C. Таким образом, на сборочную линию попадёт 6 компонентов. Во время прохождения третьего круга компонент имеется на линии А. Поэтому на сборочную линию доставляется седьмой компонент, но на линии B компонентов больше нет, и робот вынужден остановиться.
Работа робота очень плотно связана с понятием согласования работ: как организовать работу таким образом, чтобы она была выполнена правильно. Роботы запрограммированы выполнять определённый порядок операций. Также им указывается алгоритм принятия решений. Имеется даже часть, которая занимается управлением ошибок на тот случай, если что-то пойдёт не так. В данном задании отслеживается, имеются ли на следующей конвейерной линии компоненты, которые можно было бы положить на сборочную линию.
Робот-пылесос 
перемещается по окружённой стенами комнате, которая разделена на 6x7 квадратные зоны.
Робот всегда начинает работу с середины какого-нибудь квадрата в направлении какой-нибудь стены. Роботом можно управлять с помощью программы, которая состоит из следующих команд:
ВПЕРЁД: переместись на расположенный перед тобой следующий квадрат:
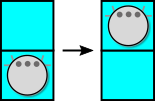
НАПРАВО: повернись на 90 градусов направо, т.е. по часовой стрелке, но останься в этом же квадрате:
НАЛЕВО: повернись на 90 градусов налево, т.е. против часовой стрелки, но останься в этом же квадрате:
Предположим, что робот работает по следующей программе:
ВПЕРЁД НАЛЕВО ВПЕРЁД НАПРАВО ВПЕРЁД
Будем считать квадрат безопасным, если стартующий с этого квадрата робот сможет всегда выполнить программу и при этом не столкнуться со стеной вне зависимости от первоначального направления робота.
Сколько безопасных квадратов существует в комнате?
[Täisarv [0, 42]]
Правильный ответ: 6.
Во время выполнения программы робот в итоге продвигается на 2 квадрата вперёд и на один квадрат налево:
Следует учитывать, что это должно быть возможным во всех четырёх направлениях. Если робот стартует с расположенного около какой-нибудь стены квадрата (так называемого крайнего квадрата) или квадрата, который соседствует с крайним квадратом, то существует по меньшей мере одно направление, двигаясь в котором по указанной программе робот столкнётся со стеной. На расположенном ниже рисунке безопасные квадраты отмечены тёмным тоном.
При написании программы программисты должны продумать все возможные ситуации, которые во время выполнения программы могут возникнуть. Они должны сфокусироваться на ситуациях, которые могут привести к аварии или неправильному поведению. Поэтому программисты должны проверить и задать необходимые первоначальные условия для работы программы, а затем протестировать программу.
Наш робот работает по тому же принципу, что и давно известный детский герой одного из первых языков программирования. Звали этого робота Карел и он появился в компьютерах более 40 лет назад. Имя было дано по имени чешского писатель Кареля Чапека. Он первым использовал в отношении интеллигентных механических работников слово "робот", и произошло это в написанной им пьесе "R.U.R." в 1920 году, то есть сто лет назад. В этой футуристической драме описывается завод, где создавали роботов, работающих на людей и во благо людей. Таким образом хотели создать рай на земле. Но ничто не вечно, и даже роботы могут начать думать своей головой...
Один из компьютеров (на рисунке наверху слева) заражён "спящим вирусом". Вирус активизируется только через три дня после заражения и затем заражает все другие компьютеры, которые с ним соединены. В каждом новом заражённом компьютере вирус также ждёт 3 дня, прежде чем активизироваться. На рисунке показано, как компьютеры соединены между собой в сети. Если компьютер уже заражён, то снова он уже не заражается.
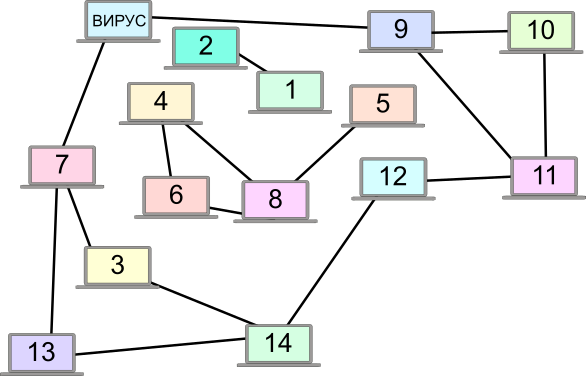
Через сколько дней сможем сказать, что в этом очаге больше не произойдёт заражения компьютеров?
[Täisarv]
Правильный ответ: 9.
Чтобы узнать количество дней, начнём с соседей заражённого компьютера: через три дня заразятся компьютеры 7 и 9.
Через шесть дней жертвами станут компьютеры 3, 13, 10 и 11.
Через девять дней заразятся последние, расположенные в этой сети, компьютеры 12 и 14.
Компьютеры 1, 2, 4, 5, 6 и 8 не соединены с заражёнными, и поэтому вирус до них не дойдёт.
Граф состоит из вершин (которые в нашем задании представлены в виде компьютеров) и соединяющих их рёбер (соединения между компьютерами). Компонентой связности называется множество вершин, соединённых между собой с помощью рёбер (в нашем задании компонентой связности является каждая отдельная компьютерная сеть). Так как вирус распространяется от компьютера к компьютеру через сетевые соединения, то заражаются только расположенные в той же сети компьютеры.
Принадлежащие компоненте связности графа вершины можно пройти разными способами. В данном задании описанный способ, при котором вирус распространяется от каждого заражённого компьютера ко всем его соседям, называется алгоритмом заливки (ingl flood fill). Название связано с тем, что распространение вируса похоже на растекание во все стороны разлитой воды. Такой же алгоритм используется, например, и в компьютерной графике для заполнения зон цветом или с помощью текстуры.
Бобрята играют в игру, которая называется "Квадратики", и они все хотят принять в ней участие. Местом проведения игры является парк, который поделён на квадраты. В парке также имеются дом и деревья - заходить в эти квадраты бобрятам запрещено. Таким образом, существует 26 пустых квадратов.
В начале игры каждый игрок находится в пустом квадрате. Дальше бобрята перемещаются таким образом, чтобы каждый игрок за время игры посетил все 26 пустых квадратов. Одновременно в каждом квадрате не может находится более одного игрока, также запрещено перемещение по диагонали.
Например, бобрята могут перемещаться следующим образом:
Каково наибольшее количество бобрят, которое сможет принять участие в проводимой в парке игре? Обратите внимание, что у каждого игрока должна быть возможность перемещаться по всем 26 пустым квадратам.
[Raadionupud]
A. 13
B. 23
C. 25
D. 26
Правильный ответ: B (23).
Задание похоже на так называемую игру в 15, где на поле размером 4x4 располагается 15 пронумерованных костяшек. Цель игры - перемещая костяшки по одной, добиться упорядочивания их по номерам. На беспрепятственном игровом поле достаточно иметь один пустой квадрат, чтобы каждую костяшку можно было переместить в каждый квадрат.
Хотя в нашем задании в правом верхнем углу за домом и имеется два квадрата, но, попав в них, бобрята окажутся в ловушке и не смогут больше перемещаться:
Также в случае двух пустых квадратов возникает ситуация, при которой один бобрёнок сможет перемещаться только между тремя верхними, расположенным справа, квадратами:
Таким образом, в этой игре не смогут принять участие 24 (или более) игрока.
Однако на приведённом ниже рисунке видно, что если будет три свободных квадрата, то все бобрята смогут перемещаться по двум, расположенными за домом, квадратами:
Получаем, что правильным ответом будет 26-3=23.
Решение задания требует аналитического мышления. После получения общего обзора, необходимо сосредоточиться на частных случаях (так называемых пограничных ситуациях), чтобы выяснить, есть ли необходимость из-за них менять первоначальное общее решение. Такой навык особенно необходим при тестировании программного обеспечения. В данном случае два расположенных наверху справа квадрата являются частным случаем, который необходимо тщательным образом проанализировать.
Из-за распространения вируса в волости должны закрыться некоторые продуктовые магазины, но в любом случае вблизи каждого посёлка должен остаться по меньшей мере один работающий магазин. Будем считать, что магазин находится вблизи посёлка, если ни один другой посёлок не окажется по дороге к магазину.
Зелёные точки обозначают посёлки, красные квадраты - продуктовые магазины, а линии между ними - дороги.
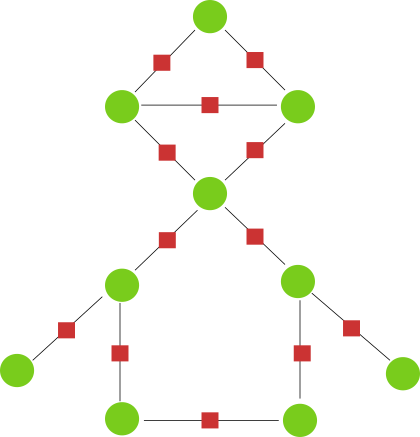
Какое минимальное количество продуктовых магазинов должна продолжить работу, чтобы вблизи каждого посёлка всё-таки остался магазин?
[Täisarv [0, 12]]
Правильный ответ: 5.
Работу обязательно должны продолжить магазины, расположенные на самом левом и самом правом краю карты, чтобы обеспечить продуктами крайние посёлки. Для обеспечения продуктами посёлков, расположенных на карте в самом низу, достаточно будет нижнего магазина. С помощью этих трёх магазинов продуктами будут обеспечены все шесть посёлков, расположенных в нижней части карты. Чтобы обеспечить продуктами верхние четыре посёлка, необходимо оставить работать ещё по меньшей мере два магазина, так как никакой из магазинов не находится поблизости от них всех. Этими двумя магазинами могут стать магазины, которые находятся в верхнем квадрате и расположены напротив друг друга.
Целью задания является оставить в графе как можно меньшее количество рёбер таким образом, чтобы все вершины были бы связаны с каким-нибудь ребром. В данном случае в роли вершин выступают посёлки, а в роли рёбер - дороги вместе с продуктовыми продуктами. Такое задание в информатике известно как задача на нахождение рёберного покрытия (англ edge cover) графа. В свою очередь идеи решения такой задачи используется во многих других алгоритмах, например, при поиске покрывающего дерева (англ spanning tree) или кратчайшего пути.
Бобры придумали набор паролей, чтобы защитить свои дома. Пароли состоят только из двух символов: 
и 
.
Контролёр пароля должен определиться, является ли он верным или неверным. Этот процесс иллюстрирует нижеприведённый рисунок:
В приведённом наверху примере верным паролем может считаться только такой:
Бобры создали нового контролёра пароля:
Какие из приведённых ниже паролей новый контролёр паролей будет считать верными?
[Märkeruudud]
A. 
B. 
C. 
D. 
E. 
Правильный ответ: A и B.
Верными будут пароли A и B, так как при их прохождении в итоге оказываются в кружке с буквой E.
Пароль C неверный, так как имеется первый символ , но все подходящие пароли должны начинаться с символа .
Пароль D неверный, так как он состоит из десяти символов, а длина всех подходящих паролей должна делиться на три; контроль останавливается до девятого символа.
Пароль E неверный, так как символ присутствует в нём 5 раз, а символ 4 раза, хотя подходящие пароли на две трети состоят из символов и на одну треть из символов ; контроль останавливается до последнего символа.
Контролёр паролей, разработанный бобрами, основывается на так называемом автомате (точнее, на детерминированном конечном автомате). Это математическая модель. Такой автомат может в каждый момент времени быть только в одном состоянии; состояние меняет приходящая со входа информация.
Автоматы применяются в различных устройствах для контроля очерёдности действий. Например, в торговых автоматах (различные шаги в процессе покупки), лифты (очерёдность остановок в соответствии с пожеланиями пользователя), светофоры (изменение режима, если машина стоит), кодовые замки (контроль последовательности введённых цифр) и т.д.
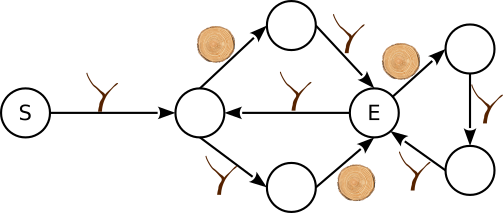
На приведённом ниже плане города видно, что имеется много улиц с односторонним движением (обозначено стрелкой с одним концом) и некоторые улицы допускают двустороннее движение.
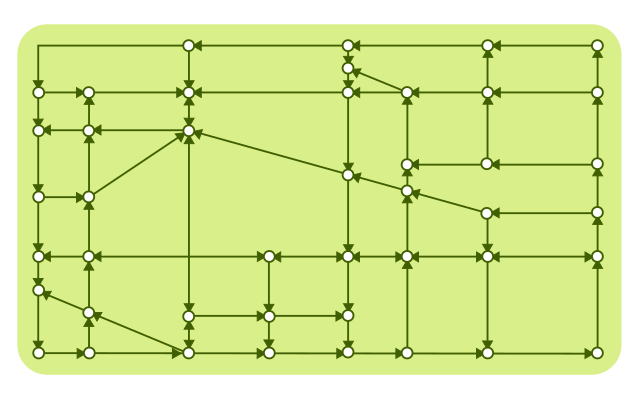
Перекрёсток, к которому можно подъехать только с одного перекрёстка, называется уязвимым.
Сколько уязвимых перекрёстков имеется на плане города?
[Täisarv [0, 44]]
Правильный ответ: 14.
Существует 14 уязвимых перекрёстков:
Такие структуры называются сетями. Сеть - это ориентированный граф, а количество стрелок, направленных в каждую из вершин, называется валентностью этой вершины. Вершина является уязвимой, если её валентность равна 1, и недоступной, если её валентность равна 0.
Атака в отношении уязвимых точек сети порождает проблемы, например, с доступом к важным услугам. Чтобы минимизировать потерю информации, анализ сети и обнаружение уязвимых мест является важной работой при проектировании сети.
У бобра Тима имеется 9 шаров и коробка с 9 ячейками:
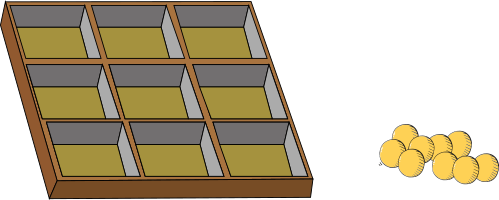
Он выбирает некоторое количество шаров в промежутке от 0 до 9 и размещает их в коробке, следуя правилам:
Сколько способ размещения шаров в коробке существует?
[Raadionupud]
A. 12
B. 16
C. 64
D. 512
Правильный ответ: B (16).
Начнём с части коробки размером 2x2 ячеек:
Всего у нас 4 ячейки, при этом в каждой ячейке шар может быть, а может и не быть. Таким образом, существует 2^4 = 16 различных возможностей для размещения шаров.
Важно отметить, что, если Тим каким-то образом заполнил эти четыре ячейки, то у него больше нет выбора в отношении оставшихся ячеек: в правилах написано, что в каждом ряду и столбце должно быть чётное количество шаров, поэтому то, как шары будут расположены в первоначальной коробке размером 2x2 определяет, как можно расположить шары между оставшимися ячейками.
Например, предположим, что Тим разместил шары в коробке размером 2x2 следующим образом:
Так как в первом столбце имеется только один шар, то Тиму придётся шар положить в ячейку A, чтобы количество шаров в столбце стало чётным. Во втором столбце уже имеется чётное количество шаров, поэтому ячейка B должна остаться пустой. Продолжая рассуждать таким же образом, мы поймём, что Тим должен оставить пустой и ячейку C, а шары положить в ячейки D и E.
Так как вариантов при заполнении коробки размером 2x2 было 16 и для заполнения оставшихся ячеек больше возможностей нет, то для заполнения шарами всей коробки имеется тоже только 16 возможностей.
Сохранение и передача данных является важной темой для информатики. Одним из способов проверки того, что во время передачи с данными ничего не случилось, является контроль чётности. Бит чётности может иметь значение 0 или 1 и рассчитывается на основании предыдущих данных (чтобы согласно договорённости подсчитать чётное или нечётное количество 1 битов); затем он добавляется в конец данных. После передачи данных вновь рассчитывается бит чётности и проверяется, является ли результат таким же. Если полученный бит чётности отличается от первоначального, то с данными что-то произошло.
В данном задании ячейки в последнем ряду и в последнем столбце и представляют собой именно такие биты чётности. Если бы эта коробка была передана дальше, то получатель смог бы проверить суммы рядов и столбцов и, если бы не получились чётные числа, то Тим получил бы сообщение об ошибке.
Бобры с номерами от 1 до 6 сидят на расположенных рядом креслах и хотят сыграть в игру. Перед началом игры выбирается одно число от одного до четырёх. После каждого хлопка бобры должны пересесть на то количество кресел в правую сторону, которое было выбрано заранее; оказавшиеся в конце цепочки бобры должны перейти в начало. После перемещения оказавшийся самым крайним с правой стороны бобр выбывает из игры, а последнее кресло убирается. Бобр, который останется самым последним, станет победителем игры.
Например, если выбрать число 2, то победит бобр под номером 6:
Бобр под каким номером станет победителем, если выбрать число 3?
[Täisarv [1, 6]]
Правильный ответ: 2.
Зачастую в программировании используются операции на уровне битов для сравнения чисел или их вычисления. Такие операции очень быстры и просты, ими оперируют на уровне процессора. Одной из форм битовой операции является круговое смещение - мы можем представить, что концы последовательности битов соединены между собой: смещение бита с одного конца строки переносит его в начало другого конца. Такой подход очень важен, если есть необходимость сохранять все биты. Такие операции часто применяются в криптографии.
Круговое смещение влево (MSB - most significant bit, наибольший значащий бит; LSB - least significant bit, наименьший значащий бит):
Круговое смещение вправо:
Бобр Максим кладёт в ряд плитки восьми различных типов. У каждой плиты имеется определённое значение:
При укладке плиток в ряд Максим должен учитывать определённые правила:
Например, на третьем месте должна быть плитка со значением 3: на первом месте располагается плитка со значением 1, на втором месте со значением 2, а сложив эти два значения, мы получим 3:
Какую плитку в этом ряду на 8ое место должен положить Максим?
[Raadionupud]
A. 
B. 
C. 
D. 
Правильный ответ: C.
Объяснение приведено на рисунке, где укладка плиток приведена начиная с 4ой:
Используемое в этом задании правило увязывает выбор следующей плитки с использованными ранее плитками. Это рекурсивный алгоритм: он "использует самого себя". В математике, например, таким же образом даётся определение чисел Фибоначчи: каждое следующее число является суммой двух предыдущих. Удивительно, но похожую последовательность мы можем наблюдать и в природе: добавление веток на дереве, размножение растений и т.д.
В отличие от классической последовательности Фибоначчи в нашем задании нет бесконечно увеличивающихся значений - у нас имеется дополнительное правило, которое замещает суммы, превышающие определённую границу, значением -2.
В информатике рекурсия является широко применяемой техникой, когда решаемое задание делится на маленькие части, которые по своей природе схожи с первоначальной задачей, но решаются легче.
В системах электронных таблиц первые 26 столбцов обозначены буквами латинского (вернее английского) алфавита:
Следующие 26 столбцов обозначены двухбуквенными комбинациями от AA до AZ:
Следующие за ними последующие 26 столбцов обозначены комбинациями от BA до BZ:
Так продолжается до тех пор, пока не закончатся двухбуквенные комбинации после ZZ. После этого начинают использовать трёхбуквенные комбинации от AAA до AAZ:
Какое обозначение имеет 2020-ый столбец?
[Raadionupud]
A. BXR
B. BYR
C. CXR
D. CYR
Правильный ответ: B (BYR).
Одним из способов решить это задание является помощь программы электронных таблиц - откроем её, установим курсор в самый первый столбец рабочего листа, 2019 раз нажмём на клавишу "стрелка вправо" и посмотрим, какое обозначение будет у соответствующего столбца. Это, конечно, нудно, и к тому же существует большой риск того, что мы можем в какой-то момент сбиться со счёта.
Другая возможность - это рассчитать для каждого предложенного варианта соответствующий номер столбца. При этом обратим внимание на то, что
с однобуквенными обозначениями имеется 26 столбцов, то есть столбцы от 1 до 26;
в двухбуквенных обозначениях для первой буквы имеется 26 вариантов, для каждой следующей за первой буквой второй буквы имеется также 26 возможных вариантов; таким образом, всего двухбуквенных обозначений будет 26*26=676; получаем, что столбцы с двухбуквенными обозначениями будут от 27 до 702;
в начинающихся на букву A трехбуквенных обозначениях количество всех возможных двухбуквенных пар для второй и третьей букв равно 676 (на основании предыдущего пункта); таким образом, столбцы с трёхбуквенными обозначениями, начинающими на букву А, будут от 703 до 1378;
в числе начинающихся на букву В перед BXR имеется ещё 23*26+17=615 столбцов: прежде всего те столбцы, где вторая буква будет от A до W (23 возможности), а для третьей буквы будут использованы буквы от A до Z (26 возможностей), и далее те столбцы, где в начале имеется BX, а в роли третьей буквы выступают буквы от A до Q (17 возможностей); таким образом, перед BXR располагаются столбцы от 1379 до 1993, а номер самого столбца BXR будет 1994;
аналогично вычислениям предыдущего пункта получим, что перед BYR имеется ещё 24*26+17=641 начинающихся на букву B трёхзначных обозначений и, таким образом, номером BYR будет искомый 2020;
для решения задания это уже не пригодится, но, действуя таким же образом, можем найти, что номер столбца CXR будет 2670, а номером столбца CYR - 2696.
В вычислительных системах постоянно необходимо преобразовывать обозначения различных объектов. Самым обычным примером можно считать преобразование привычной для человека десятичной системы в двоичную систему, используемую компьютерами.
Например, если в 10-ой системе запишем 345, то это обозначает выражение
310^2 + 410^1 + 5*10^0 = 300+40+5 = 345.
Представление этого же числа в 2-ой системе было бы 101011001, и выражение было бы
12^8 + 02^7 + 12^6 + 02^5 + 12^4 + 12^3 + 02^3 + 02^1 + 1*2^0 = 256+64+16+8+1 = 345.
В обозначении столбцов таблицы использовано 26 "цифр" от A до Z и, таким образом, у нас используется 26-ая система, где доля каждого следующего разряда в 26 раз больше доли предыдущего разряда. Однако в отличие от классической позиционной системы счисления, где значения 26 цифр могут быть от 0 до 25, в обозначение столбцов их значения могут быть от 1 до 26.
Зная эту особенность, можно было указанное в объяснении к заданию пошаговое решение рассчитать напрямую (используя в виде подсказки значений букв первый рисунок, приведённый в тексте задания):
BXR = 226^2 + 2426^1 + 1826^0 = 1352 + 624 + 18 = 1994, BYR = 226^2 + 2526^1 + 1826^0 = 1352 + 650 + 18 = 2020, CXR = 326^2 + 2426^1 + 1826^0 = 2028 + 624 + 18 = 2670, CYR = 326^2 + 2526^1 + 1826^0 = 2028 + 650 + 18 = 2696.
На узкой стоянке машины могут выполнять следующие манёвры:
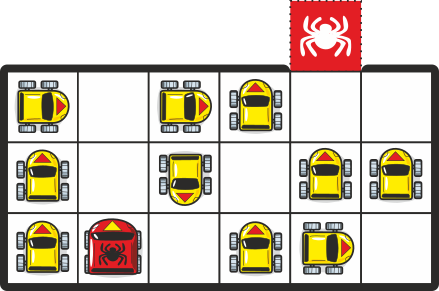
Для того, чтобы красная машина смогла выехать с парковки, потребуется перемещение и других машин.
Какое наименьшее общее количество манёвров потребуется от всех машин, чтобы красная машина смогла добраться до красного квадрата?
[Raadionupud]
9
11
13
15
Правильный ответ: B (11).
Красная машина сможет выехать с парковки за следующие 11 манёвров:
Теперь необходимо убедиться, что 11 является действительно наименьшим возможным количеством манёвров.
Прежде всего, представим себе, что красная машина - это единственная машина на парковке. В таком случае для того, чтобы выехать с парковки, необходимо проехать 2 квадрата в направлении севера и 3 квадрата в направлении востока, а также совершить 2 поворота. Машина может сделать эти манёвры в разных последовательностях, но в любом случае необходимо сделать все 8 манёвров.
Так как на парковке имеются и другие машины, то для проезда красной машины их также необходимо переместить.
Прежде всего, проезд красной машине блокируют три машины, выставленные в форме L. Чтобы проехать этот участок, достаточно будет сделать один манёвр:
Далее проезд красной машине блокируют следующие три машины, выставленные в форме L. Разблокировать этот участок за один манёвр не получится, но за два можно:
Таким образом, чтобы красная машина смогла выехать с парковки, необходимо сделать 8+1+2 = 11 манёвров.
Это задание относится к числу заданий на оптимизацию: нам надо не просто решить задание, а решить его наилучшим возможным способом. В таких заданиях самой трудной частью зачастую является доказательство оптимальности найденного решения.
Во многих случаях единственной возможностью для этого является просмотр всех возможных вариантов (англ exhaustive search): найдём все возможные решения и покажем, что все другие будут хуже, чем наше решение. В некоторых случаях проверка всех вариантов вручную является очень большой работой, но она посильна компьютерам. Однако во многих заданиях количество возможных вариантов настолько велико, что их проверка даже с помощью компьютера заняла бы слишком много времени. В таких случаях следует воспользоваться сложными алгоритмами, такими как обрезка дерева поиска (ingl search tree pruning) или метод ветвей и границ (ingl branch and bound), или итеративное углубление (ingl iterative deepening).
Иногда в задании можно найти некоторые особые условия (как например в этом задании три машины, выставленные в форме L), с помощью которых оптимальность решения можно показать без изучения других вариантов. Случается, что эти особые условия являются специфическими для одного конкретного случая (например, если бы жёлтые машины были расположены по-другому, то рассуждение про три машины, выставленные в форме L, не привели бы к желаемому результату), а иногда удаётся найти общие условия (так называемые инварианты), которые показывают, что с помощью одного метода или системы составленное решение является наилучшим возможным. Например, в некоторых заданиях на оптимизацию лучшее решение можно получить с помощью так называемого жадного алгоритма (англ greedy algorithm), который на каждом этапе совершает кажущийся самым полезным шаг без учёта какой-нибудь далеко идущей стратегии.
Печатная машинка может распознать пять картинок, которые представляют собой буквы I, T, O, C и L.
Для распознавания печатная машинка использует так называемые тепловые карты. Цвет каждого пикселя (точки) на тепловой карте картинки указывает на уникальность использованного в этом месте картинки цвета по отношению к другим картинкам: чем уникальнее цвет пикселя картинки, тем светлее будет пиксель на тепловой карте.
Уникальный: ни на одной другой картинке в этом месте нет пикселя с таким же цветом.
Скорее уникальный: только на одной из других картинок в этом же месте имеется пиксель того же цвета.
Не уникальный: на двух других картинках в этом же месте имеется пиксель того же цвета.
Скорее обычный: на трёх других картинках в этом же месте имеется пиксель того же цвета.
Обычный: на всех картинках в этом же месте имеется пиксель того же цвета.
Например, картинке 
соответствует тепловая карта 
.
Какой картинке соответствует тепловая карта 
?
[Raadionupud]
A. 
B. 
C. 
D. 
Правильный ответ: B.
На изучаемой тепловой карте во втором ряду третьего столбца имеется белый пиксель. Это означает, что этот пиксель на одной из букв отличается от всех остальных.
является единственной картинкой, у которой в этом месте имеется отличающийся от всех других картинок чёрный пиксель; на всех других картинках этот пиксель имеет белый цвет.
Далее приведены все буквы с соответствующими им тепловыми картами:
Тепловые карты (англ heat map) являются одной из форм графического представления данных, где числовые значения заменены на цветовой код. Такие карты мы могли наблюдать в сообщениях о погоде, где с помощью цвета обозначают температуру или количество осадков в разных районах.
Аналогично данному заданию тепловые карты также используются при распознавание фотографии, где, например, с при тренировке искусственной нейронной сети обращается внимание на определённые области фотографии.
В Бобруйске для обозначения чисел используются только нули и единицы. Два бобрёнка решили найти подарок маме на день рождения. На двоих у них было 11000101 бобриков денег. Дети нашли три возможных подарка: шарф стоимостью 1110110 бобрика, ожерелье стоимостью 11001000 бобрика и часы стоимостью 10011101 бобрика.
Какой самый дорогой подарок смогут приобрести дети на имеющиеся у них деньги?
[Raadionupud]
A. Шарф
B. Ожерелье
C. Часы
Правильный ответ: C (часы).
Из имеющихся подарков ожерелье стоит больше, чем есть денег у детей: 11001000 > 11000101. Для оставшихся вещей у них имеется достаточное количество денег: 1110110 < 11000101 и 10011101 < 11000101. Таким образом, они могут купить шарф или часы. Из них двоих самыми дорогими будут часы: 1110110 < 10011101.
Задание связано с двоичной системой. В двоичной системе, в отличие от привычной для нас десятичной системы, для обозначения чисел используются только две цифры: 0 и 1. Существуют и другие системы счисления. Например, восьмеричная система (цифры 0-7) или шестнадцатеричная система (цифры 0-9 и в дополнении к ним буквы A, B, C, D, E и F).
Компьютеры используют двоичную систему из-за её простоты. Мы можем представить цифру 0 как отсутствие сигнала (выключатель в положении "выкл") и цифру 1 как наличие сигнала (выключатель в положении "вкл"). Таким образом, благодаря различным последовательностям состояний, мы можем записать различные числа. В двоичные числа можно преобразовать и другие данные (например, буквы) - последовательность 01101000 может обозначать число 104 или букву "h".
Митя хочет опубликовать на сайте школы диаграммы результатов опроса учеников. Графический редактор позволяет сохранять изображения в различных форматах.
Какой из следующих форматов следует использовать для диаграмм?
[Raadionupud]
A. Windows Bitmap (*.bmp)
B. Encapsulated PostScript (*.eps)
C. Joint Picture Experts Group image format (*.jpg)
D. Portable Network Graphics (*.png)
Правильный ответ: D (PNG).
Для публикации диаграммы в Интернете из предложенных вариантов лучше всего подходит формат PNG. Это формат растровой графики, где каждая картинка представлена в виде маленьких разноцветных квадратиков. PNG формат основывается на сжатии без потерь. Это означает, что при восстановлении получим точно такие же первоначальные данные. Данный формат очень подходит для представления "искусственных" рисунков, состоящих из больших участков с однородным цветом или повторяющимся узором, или имеющих контрастные линии. Именно так и выглядят диаграммы. Также PNG формат поддерживается всеми современными браузерами, которые доступны в операционных системах для настольных компьютеров, планшетов и телефонов.
JPEG также является растровым форматом, но сжатие происходит с потерями. JPEG был создан для того, чтобы представлять "естественные" рисунки, как, например, фотографии, где много различных тонов и плавных переходов между ними. Если для сохранения рисунков с контрастными чёткими линиями использовать этот формат, то применяемый алгоритм сжатия приведёт к довольно большим искажениям (это видно на приведённом ниже сравнении). По этой причине этот формат не очень подходит для "искусственных" рисунков (графиков, чертежей, скриншотов).
BMP является растровым форматом без потерь, как и PNG, но основывается на более простых алгоритмах сжатия и поэтому сохранённые в этом формате файлы имеют больший размер, чем при сохранении точно такого же рисунка в формате PNG. Например, размер файла с одной примерно 600х350 пиксельной столбчатой диаграммой в формате PNG будет около 8 KB, а в формате BMP более 600 KB. Стоит учитывать, что BMP является форматом, специфичным для Windows, и поэтому не обязательно будет поддержан в браузерах других операционных систем.
EPS отличается от всех вышеописанных форматов, потому что это формат векторной графики. Это означает, что имеющиеся в EPS-файле рисунки описываются не с помощью мозаики из пикселей квадратной формы, а с помощью объектов, состоящих из геометрических фигур (линий, прямоугольников, кругов и др.). Благодаря этому рисунки в векторном формате можно увеличивать и уменьшать без изменения качества. В приведённой ниже сравнительной таблице видно, что при увеличении представленных в формате PNG и BMP рисунков они становятся квадратоподобными, а в случае JPEG формата рисунок становится нечётким. В то же время рисунок в векторном формате остаётся чётким. Недостатком EPS формата является то, что он исторически был очень сложным форматом, применявшимся в типографии, и сейчас не поддерживается браузерами (для просмотра рисунков в этом формате необходима отдельная программа).
Scalable Vector Graphics (*.svg) является современным форматом векторной графики и предназначен для использования в Интернете. У этого формата в общем схожие с EPS форматом позитивные свойства и, если программное обеспечения для создания диаграмм поддерживает этот формат, предпочтительнее использовать именно его. Однако стоит иметь ввиду, что это довольно новый и находящийся ещё в процессе развития файловый формат, поэтому в случае некоторых сложных рисунков может получиться так, что все браузеры не смогут их достоверно отобразить.
| PNG/BMP (увеличение) | JPEG (увеличение) | SVG/EPS (увеличение) |
|---|---|---|
 |
 |
 |
Если одни и те же данные можно представить в разных форматах, как это, например, и есть в случае графики, то при выборе правильного формата надо знать его позитивные и негативные стороны.
Copyright © 2020 Bebras – International Challenge on Informatics and Computational Thinking.
Licensed under Creative Commons Attribution-ShareAlike 4.0 International License.
Flag icons by GoSquared.