Madis sai endale programmeeritava seadme, millel on kolm lampi: punane, roheline ja sinine. Kõik lambid on algselt välja lülitatud, kuid neid saab programmi abil põlema panna.
Väike näide programmist:
REPEAT: turn_on(RED_LED); wait(1s); turn_off(RED_LED); wait(2s);
See programm käitub järgmiselt:
Madis leidis internetist uue programmi ja tahab seda proovida.
REPEAT: turn_on(BLUE_LED); wait(2s); turn_on(RED_LED); turn_on(GREEN_LED); wait(2s); turn_off(GREEN_LED); turn_off(BLUE_LED); wait(2s); turn_on(GREEN_LED); wait(2s); turn_off(RED_LED); turn_off(GREEN_LED);
Mitu lampi põlevad 13 sekundit pärast selle programmi käivitamist?
[Täisarv [0, 3]]
Õige vastus on: 1.
Vastust aitab selgitada järgnev diagramm, kus on ajateljele paigutatud kolme lambi põlemisgraafikud. Iga graafiku kõrgem asend näitab, et lamp põleb, ja madalam asend, et see ei põle. Nagu näha, 13 sekundit pärast programmi käivitamist punane lamp põleb, roheline ja sinine aga ei põle.
Sellise diagrammi koostamiseks on kõige lihtsam vaadata iga lambi olekut eraldi. Näiteks punase lambi graafiku leidmiseks jätame programmist välja kõik rohelise ja sinise lambiga seotud sammud:
REPEAT: wait(2s); turn_on(RED_LED); wait(2s); wait(2s); wait(2s); turn_off(RED_LED);
Nüüd on lihtne näha, et punase lambi graafik on: 2 sekundit kustunud olekus, 2+2+2=6 sekundit põlevas olekus, ja siis jälle otsast peale.
Analoogiliselt saame koostada ka rohelise ja sinise lambi gaafikud.
Programmikoodi mõistmine on informaatikas tähtis. Antud ülesandes on kasutatud nn. protseduurilist programmeerimiskeelt, sarnast keelt kasutab ka näiteks Arduino, mis on saanud väga populaarseks programmeerimise õppimise vahendiks.
Siin ülesandes peab mõistma programmi ja simuleerima selle tööd. See on oluline tegevus iga programmeerija jaoks, eriti selleks, et leida põhjus, miks programm töötab teisiti kui oodatud.
Keerulisemate programmide analüüsimisel on sageli kasulik keskenduda programmi käitumise ühele aspektile korraga, nagu selles ülesandes on tehtud iga lampi eraldi analüüsides.
Palgijuppidest tehtud raja abil sood ületades kohtus kobraste grupp kängurutega, kes ületasid sood samal viisil, kuid vastassuunas. Keegi ei tahtnud märjaks ega räpaseks saada, nii jäid kõik palkide peale ootama. Kängurud leidsid raja kõrvalt kivi, millele sai palgi pealt hüpata ja millelt suudeti ka samale palgile tagasi tulla. Kivile suutsid hüpata vaid kängurud ja korraga mahtus kivile vaid üks neist.
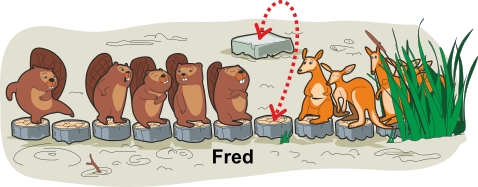
Ei kobrastel ega kängurutel polnud midagi selle vastu, et liikuda ka tagurpidi, ainult peakobras Fred, kes kohtus kängurutega esimesena, oli nõus taganema kokku vaid 10 sammu.
Kui palju känguruid saab Fredist mööduda, kui arvestada Fredi nõudmisi?
[Raadionupud]
A. Fredist saab mööduda rohkem kui 10 kängurut.
B. Fredist saab mööduda täpselt 10 kängurut.
C. Fredist saab mööduda täpselt 6 kängurut.
D. Fredist saab mööduda täpselt 4 kängurut.
E. Fredist saab mööduda vähem kui 4 kängurut.
F. Sellele küsimusele pole võimalik vastata.
Õige vastus on: C.
Me võime momendil ignoreerida kõiki teisi kopraid peale Fredi. Kui känguru soovib Fredist mööduda, tehakse järgmised sammud.
Känguru hüppab kivile:
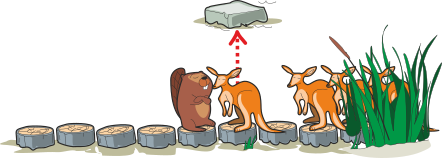
Fred läheb kaks sammu edasi:
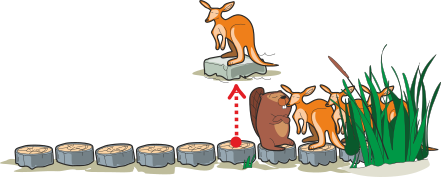
Känguru hüppab tagasi rajale ja võib teekonda jätkata:
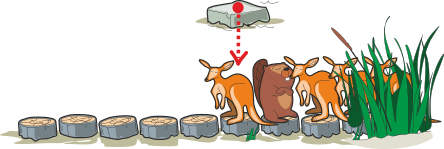
Fred läheb kaks sammu tagasi, et anda järgmisele kängurule võimalus kivile hüpata:
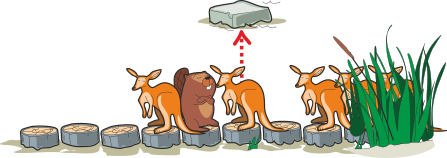
Kui neid samme läbida viis korda, laseb Fred mööduda viiel kängurul, tehes ise kokku kümme sammu tagasi. Ka kuues känguru saab mööduda, kuna Fred peab tema möödumiseks astuma ainult 2 sammu edasi, kuid mitte enam tagasi.
Lahendust võime kirjeldada ka matemaatilise võrrandi abil: kui Fred soovib lasta mööduda K kängurul, peab ta tagasi liikuma S = 2 x (K – 1) sammu. Kui avaldada sellest võrrandist kängurude arv, siis saame K = S / 2 + 1.
Väike kobras Juku mängib klotsidega. Kõik klotsid on ühesuguse kõrgusega, kuid klotside laiused on erinevad. Juku ehitab üheksa suurepärast torni, igaüks neist on tehtud ühesuguse laiusega klotsidest.
Torni kõrguse muutmiseks on kaks võimalust: klotse torni tippu juurde lisada või neid sealt eemaldada. Mõlemal juhul kulutatakse selle jaoks energiat, mis sõltub torni laiusest ja eemaldatavate klotside arvust. Näiteks selleks, et eemaldada kaks klotsi tornist, mille laius on 1, kulub 2x1=1 ühikut energiat, ja 4 klotsi lisamine tornile, mille laius on 3, nõuab 4x3=12 ühikut energiat.
Juku tahab tornid ümber ehitada nii, et kõik oleksid ühesuguse kõrgusega, kuid soovib selleks kulutada võimalikult vähe energiat.
Mitu ühikut energiat on minimaalselt vaja ümberehituseks, et kõik tornid oleksid sama kõrgusega?
[Täisarv [0, 100]]
Õige vastus on: 39.
Kui tähistame klotside lisamist märgiga 
ja eemaldamist märgiga 
, siis oleks õige lahendus selline:
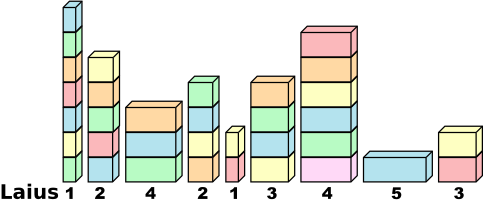
Tornide mediaankõrgus on 4 (1 2 2 3 4 4 5 6 7) ja võiks arvata, et mediaankõrguse valimine kõigi tornide ühiseks kõrguseks on optimaalne, kuid praegusel juhul see nii ei ole. Probleem on selles, et klotsidel on erinev laius.
| Laius | 1 | 2 | 4 | 2 | 1 | 3 | 4 | 5 | 3 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Algne kõrgus | 7 | 5 | 3 | 4 | 2 | 4 | 6 | 1 | 2 | Energiakulu kokku |
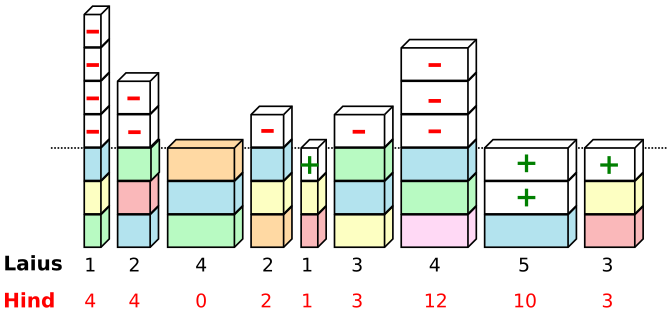
| Kõrgus 1 | 6 | 8 | 8 | 6 | 1 | 9 | 20 | 0 | 3 | 61 |
| Kõrgus 2 | 5 | 6 | 4 | 4 | 0 | 6 | 16 | 5 | 0 | 46 |
| Kõrgus 3 | 4 | 4 | 0 | 2 | 1 | 3 | 12 | 10 | 3 | 39 |
| Kõrgus 4 | 3 | 2 | 4 | 0 | 2 | 0 | 8 | 15 | 6 | 40 |
| Kõrgus 5 | 2 | 0 | 8 | 2 | 3 | 3 | 4 | 20 | 9 | 51 |
| Kõrgus 6 | 1 | 2 | 12 | 4 | 4 | 6 | 0 | 25 | 12 | 66 |
| Kõrgus 7 | 0 | 4 | 16 | 6 | 5 | 9 | 4 | 30 | 15 | 89 |
Eelnevas tabelis on leitud kõigi ümberehitusvariantide energiakulu. Muidugi ei pea me läbi vaatama kõiki variante, kuna energiakulul on üks miinimum. Võime alustada näiteks mediaankõrgusest 4 ja võrrelda selle energiakulu kõrguste 3 ja 5 energiakuludega. Kuna kõrguse 3 kulu on väiksem, peab miinimum olema sealpool. Kui võrdleme lisaks veel kõrguse 2 energiakulu, näeme, et see on kõrguse 3 kulust jälle suurem ja seega peabki 3 olema optimaalne kõrgus.
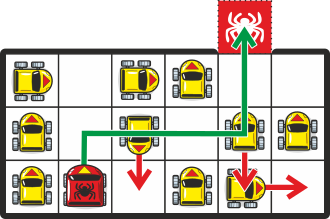
Kobras Mart läks igal nädalal korraldatavale turule. Seal kohtas ta kaht teist kobrast, nimelt kopraid k1 ja k2. Koprad k1 ja k2 kohtusid omakorda samuti kahe kopraga. Nüüd võib küsida, palju kopraid pidi turul minimaalselt olema, et koprad Mart, k1 ja k2 saaksid igaüks kohtuda kahe kopraga?
Me võime esitada kopraid ja nende kohtumisi sellise joonisena:
Sellisel juhul pidi turul olema vähemalt viis kobrast.
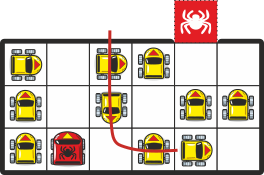
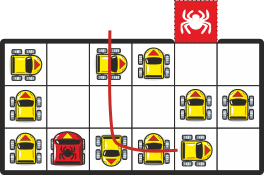
Samas on võimalikud ka teised variandid:
Neil juhtudel peab turul olema vähemalt 4 (vasakpoolne joonis) või 3 (parempoolne joonis) kobrast. Seega minimaalne kobraste arv turul on ilmselt 3.
Järgmisel nädalal läks kobras Mart uuesti turule ja kohtus seal kolme teise kopraga, kelle kohtumiste arvud samal päeval olid aga vastavalt kaks, viis ja viis.
Kui palju kopraid pidi minimaalselt sel päeval turul olema?
[Täisarv [0, 15]]
Õige vastus on: 7.
Kui me loendame Marti ja neid kopraid, kellega ta kohtub (k1, k2 ja k3), saame kokku 4 kobrast.
Vaatame nüüd lähemalt kobrast k1, kes kohtub kahe kopraga. Meil on vaja leida vähim kobraste arv, nii peame eeldama, et k1 kohtus Mardiga ja lisaks kas k2-ga või k3-ga. Kui nii, siis on piisav kobraste arv jätkuvalt neli.
Nüüd vaatame kobrast k2, kes kohtus viie kopraga. Me teame, et ta kohtus Mardiga ja võimalik, et ka k1-ga. Kui me eeldame, et k2 kohtus k1-ga ja k3-ga, peab olema veel vähemalt kaks kobrast k4 ja k5, kellega k2 kohtus. Nii tõuseb minimaalne arv kuueni.
Lõplik arv ei saa siiski olla 6, sest k1 kohtus vaid kahe kopraga, seega (lisaks Mardile) kas k2-ga või k3-ga (või mitte kummagagi neist). Kuna me eeldasime, et k1 kohtus Mardiga ja k2-ga, siis ei saanud ta kohtuda k3-ga. Nii jääb k3 võimalikku nimekirja vaid Mart, k1 ning k4 ja k5, kellega kohtus ka k2, seega peab k3 kohtuma veel ühe "uue" kopraga k6. Nii saame lõplikuks vastuseks 7.
Võime joonistada ka 7 tipuga graafi, et aidata probleemi lahendada ja tõestada, et lahendus 7 kopraga sobib.
Selles ülesandes kasutasime lahendamiseks graafi. Graaf koosneb tippudest ja neid ühendavatest servadest. Graafid võivad olla nii suunamata (tippude vahel pole hierarhiat ja servadel puudub suund) kui suunatud (servadele on omistatud suund).
Antud ülesande puhul me koostame graafi: tipud tähistavad kopraid ja servad nende kohtumisi teiste kobrastega. Graaf on suunamata, kuna kohtumine on sümmeetriline: kui üks kobras kohtub teisega, siis teine kohtub samal ajal ka esimesega. Suunatud graafi võiksime kasutada näiteks sel puhul, kui koprad mitte ei kohtuks omavahel, vaid näeksid teisi: sel juhul võiks üks kobrast teist näha, kuid teine ei pruugi näha esimest.
Graaf on võimas vahend keeruliste probleemide esitamiseks lihtsal moel. Graafe kasutatakse näiteks võrkude kujutamisel, olgu need linnatänavad, telefoni- või elektrivõrgud vms. Samuti võime graafina esitada ka sotsiaalseid võrke nagu näiteks LinkedIn või Facebook: tippudeks on kontod koos isiku kasutajanime, nime, soo jm infoga, servad aga näitavad seoseid kontode vahel.
Igal elusolendil on DNA, mis määrab ära tema geenid. DNA on nukleotiidide järjend ning erinevaid nukleotiide on neli: adeniin (A), guaniin (G), tsütosiin (C) ja tümiin (T). DNA võib muteeruda uuteks järjenditeks, mis erinevad originaalist.
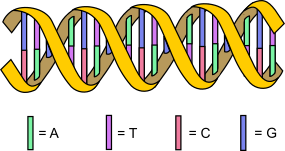
Kobru on olend, kelle DNA võib muteeruda kolmel viisil:
Milline antud nukleotiidijärjenditest EI SAA olla kobru DNA pärast kolme mutatsiooni, kui kobru algne DNA on GTATCG?
[Raadionupud]
A. GCAATG
B. ATTATCCG
C. GAATGC
D. GGTAAAC
Õige vastus on: D (GGTAAAC).
Variant A: GTATCG - asendumine (T asemel C) – GCATCG - asendumine (T asemel A) – GCAACG - asendumine (C asemel T) – GCAATG.
Variant B: GTATCG - asendumine (G asemel A) – ATATCG - dubleerumine (T) – ATTATCG - dubleerumine (C) – ATTATCCG.
Variant C: GTATCG - asendumine (T asemel A) – GAATCG - asendumine (C asemel G) – GAATGG - asendumine (G asemel C) – GAATGC.
Variandid A, B ja C on seega saavutatavad 3-sammulise mutatsiooniga.
Kuid variandi D jaoks peab läbi tegema 4 sammu: GTATCG - dubleerumine (G) - GGTATCG - dubleerumine (A) - GGTAATCG - asendumine (T asemel A) - GGTAAACG - kustumine (G) - GGTAAAC.
Ülesande lahendamiseks peame leidma iga lõppjärjendi kauguse algsest, kus kaugust loeme mutatsioonisammude arvuna.
Üldiselt tuleb selleks läbi vaadata kõik mutatsioonid, mida saame esialgsest järjendist ühe sammuga, siis kõik need, mille saame neist omakorda ühe sammuga (ehk siis esialgsest kahe sammuga) jne. Asjata töö mahtu saame vähendada sellega, et kui mingil hetkel saame järjendi, mida oleme juba varem kohanud, siis selle jätame kohe kõrvale (sest meil on juba teada lühem tee selle järjendi saamiseks algsest).
Selline mutatsioonisammudena mõõdetav kaugus on arvutiteaduses tundud kui Levenshteini kaugus. Selle klassikalises variandis on ühe teksti teiseks muutmisel lubatud operatsioonideks tähe lisamine, tähe kustutamine ja tähe asendamine teisega. Meie ülesandes on tähe lisamine asendatud nukleotiidi dubleerimisega, aga erinevates rakendustes tuleb ette ka muid variatsioone.
Koprad lõid paroolide komplekti, et kaitsta oma maju. Paroolid koosnevad vaid kahest sümbolist: 
ja 
.
Paroolikontrollija peab otsustama, kas parool on õige või vale, selle tööd illustreerib joonis:
Eeltoodud näites loetakse õigeks parooliks vaid sellist:
Koprad lõid uue paroolikontrollija:
Koprad võtsid kasutusele mitu sümbolikomplekti, et luua paroole.
Millistest toodud komplektidest saab luua parooli, mida uus paroolikontrollija aktsepteerib?
Ära peab kasutama kõik komplektis olevad sümbolid.
[Märkeruudud]
A. 4 x , 8 x
B. 2 x , 4 x
C. 5 x , 8 x
D. 5 x , 7 x
Õige vastus on: A ja B.
Vastused A ja B on õiged. Sobivad paroolid sisaldavad sümboleid kaks korda rohkem kui sümboleid .
Vastus C on vale: see koosneb 13 sümbolist, aga aktsepteeritud paroolide pikkus peab jaguma kolmega.
Vastus D on vale: parool sisaldaks 7 korda sümbolit ja 5 korda sümbolit , kuid sobivad paroolid peavad sisaldama sümboleid kaks korda rohkem kui sümboleid .
Kobraste paroolikontroll on ülesehitatud nn. olekumasinana (täpsemalt lõpliku determineeritud automaadina). See on matemaatiline mudel. Selline masin saab olla igal ajamomendil ainult ühes toodud olekutest, olekut muudab sisendist tulev info.
Olekumasinaid kasutatakse tegevuste järjekorra kontrollimisel erinevate seadmete juures, näiteks müügiautomaadid (ostuprotsessi erinevad sammud), liftid (peatuste järjekord vastavalt kasutajate soovidele), valgusfoorid (režiimi muutmine, kui auto on ootel), koodlukud (sisestatud numbrijärjendi kontroll) jne.
Tehas valmistab erinevaid tooteid, mis läbivad töö käigus mitut tehase osakonda. Kogu tootmisprotsessi tehases illustreerib skeem, kus ristkülikud tähistavad osakondi ja nooled toodete liikumist ühest osakonnast teise.
Osakondi on kaht tüüpi: tootmisosakonnad ja pakkimisosakonnad.
või 
.Tingimused tootmisprotsessis:
Milline järgnevatest skeemidest kujutab neile tingimustele vastavat tootmisprotessi?
[Raadionupud]
A.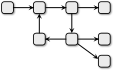 
B.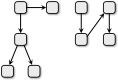 
C.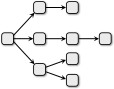 
D.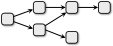 
E.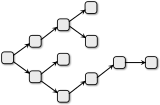 
Õige vastus on: E.
Variant A pole korrektne, sest üks osakond saab sisendit rohkem kui ühest kohast ja üks osakond saadab väljundi rohkem kui kahte kohta.
Variant B pole korrektne, sest on kaks osakonda, mis ei saa üheltki teiselt sisendit, aga selliseid tohib olla ainult üks.
Variant C pole korrektne, sest üks osakond saadab väljundi rohkem kui kahte osakonda.
Variant D pole korrektne, sest üks osakond saab sisendit rohkem kui ühest kohast.
Variant E on korrektne, kuna on täpselt üks lähteosakond (mis ei saa sisendit teistelt osakondadelt), iga muu osakond saab sisendi ainult ühest kohast, ja mitte ükski osakond ei saada väljundit rohkem kui kahte osakonda.
Informaatikas nimetatakse selliseid skeeme graafideks. Graaf on andmestruktuur, mida kasutatakse objektide ja nende vaheliste suhete kujutamiseks. Praegusel juhul on objektideks osakonnad ja nooled osakondade vahel tähistavad toote saatmist ühest osakonnast teise. Graafe kasutatakse informaatikas tihti erinevates situatioonides, näiteks võrkude kavandamisel. Praktiliste olukordade abstraktne kujutamine võimaldab kasutada ühte algoritmi paljude erinevate rakenduslike ülesannete lahendamiseks.
Selles ülesandes kirjeldatud tootmisprotsessi tingimused määravad, et protsessi kujutav graaf peab olema puu: see on sidus (lähteosakonnast saab nooli mööda liikudes igasse teise osakonda) ja selles pole tsükleid (mistahes osakonnas alustades ei saa nooli mööda liikudes jõuda tagasi samasse kohta). Sellised graafid võimaldavad kujutada hierarhilisi suhteid, nagu näiteks sugupuu, kus nooli mööda saab liikuda keskselt isikult kõigi tema esivanemateni.
Robot tegutseb pikal kitsal maa-alal. Maa-ala on jagatud nummerdatud ruutudeks, mida on lõpmatult palju:
Ese asub ühes nummerdatud ruutudest ja robot võib seda liigutada vastavalt teatud käskudele. Pärast käsu täitmist robot eseme algset asukohta enam ei mäleta.
Robot saab käske TÄIDA ja TÜHISTA. Kui robot saab käsu "TÄIDA reegel 1", siis liigutab ta eset vastavalt reeglile 1. Kui robot saab käsu "TÜHISTA reegel 1", siis peab ta taastama olukorra, mis oli enne reegli 1 rakendamist. Käsku TÜHISTA saab kasutada ainult vahetult pärast sama reeglit sisaldavat käsku TÄIDA. Samas pole kõik reeglid tühistatavad.
Olgu meil näiteks kaks reeglit:
Kui robot saab käsu "TÄIDA reegel 1", viib ta eseme ruudu võrra paremale. Käsu "TÜHISTA reegel 1" täitmiseks piisab, kui viia ese ruudu võrra vasakule, seega on reegel 1 tühistatav.
Kui robot saab käsu "TÄIDA reegel 2", viib ta eseme esimesse ruutu. Kuna robot pärast seda ei mäleta, millises ruudus ese enne oli, pole reegel 2 tühistatav.
Millised järgmistest reeglitest on tühistatavad?
[Märkeruudud]
A. Kui ese asub ruudus, mille number on suurem kui 8, siis vii see ühe ruudu võrra paremale, vastasel juhul jäta ese samasse ruutu.
B. Kui ese asub ruudus, mille number on suurem kui 8, siis vii see ühe ruudu võrra vasakule, vastasel juhul jäta ese samasse ruutu.
C. Kui ese asub paarisarvulise numbriga ruudus, siis vii see kahe ruudu võrra paremale, vastasel juhul aga ühe ruudu võrra vasakule.
D. Kui ese asub paarisarvulise numbriga ruudus, siis vii see kahe ruudu võrra paremale, vastasel juhul aga kahe ruudu võrra vasakule.
Õige vastus on: A ja D.
Reegli A rakendamisel erinevates ruutudes olevatele esemetele saame sellised tulemused:
Kui ese asus ruudus, mille number on suurem kui 8, siis tema uue asukoha number on suurem kui 9 (sinised nooled). Kui tema algasukoha number oli 8 või väiksem, siis jäi ta samasse ruutu (punased nooled). Seega on need kaks juhtu kergesti eristatavad ja reegli A tühistamise võiks kirja panna kujul "Kui ese on ruudus, mille number on suurem kui 9, siis vii see ühe ruudu võrra vasakule, vastasel juhul jäta ese samasse kohta".
Reegli D rakendamisel saame sellise tulemuse:
Kui ese oli enne paarisarvulise numbriga ruudus, asub see nüüdki paarisarvulise numbriga ruudus (sinised nooled); kui see aga oli paarituarvulise numbriga ruudus, siis asub see ka lõpuks paarituarvulise numbriga ruudus. Ka siin on võimalik eristada neid kahte juhtu ja reegli D tühistamiseks sobib "Kui ese asub paarisarvulise numbriga ruudus, siis vii see kahe ruudu võrra vasakule, vastasel juhul aga kahe ruudu võrra paremale".
Vaatame nüüd, miks pole teised reeglid tühistatavad.
Reegli B rakendamisel saame sellise tulemuse:
Kui ese oli ruudus 8, siis jäi see samasse ruutu (punane nool), kui aga ese oli ruudus 9, siis viidi see ühe ruudu võrra vasakule ehk ruutu 8 (sinine nool). Seega ei saa pärast reegli rakendamist öelda, kas ruudus 8 asuv ese oli enne samas ruudus või liikus sinna ruudust 9 ja nii polegi reegel B tühistatav.
Reegli C rakendamisel saame sellise tulemuse:
Kui ese oli enne paarisarvulise numbriga ruudul, siis on see paarisarvulise numbriga ruudul ka pärast reegli rakendamist (sinised nooled); kui see aga oli paarituarvulise numbriga ruudul, siis satub ta samuti paarisarvulise numbriga ruudule (punased nooled). Seega ei saa ka siin üheselt otsustada, millisel ruudul asus ese eelnevalt, nii pole ka reegel C tühistatav.
Anna, Bruno ja Carmen on tehase ainukesed kolm töölist. Nad lähevad tööle vastavalt kindlaksmääratud nõuetele. Igal esmaspäeval peab tööle minema täpselt kaks töölist, teistel päevadel aga vastavalt järgmistele reeglitele:
Tootmise optimeerimiseks võib erinevatel päevadel olla vaja erinevat arvu töölisi. Milline järgnevatest nädalaplaanidest on eelkirjeldatud reeglite järgimisel võimalik?
[Raadionupud]
| Esmaspäev | Teisipäev | Kolmapäev | Neljapäev | Reede | |
|---|---|---|---|---|---|
| Töölisi | 2 | 3 | 1 | 1 | 2 |
| Esmaspäev | Teisipäev | Kolmapäev | Neljapäev | Reede | |
|---|---|---|---|---|---|
| Töölisi | 2 | 1 | 3 | 2 | 1 |
| Esmaspäev | Teisipäev | Kolmapäev | Neljapäev | Reede | |
|---|---|---|---|---|---|
| Töölisi | 2 | 1 | 3 | 1 | 0 |
| Esmaspäev | Teisipäev | Kolmapäev | Neljapäev | Reede | |
|---|---|---|---|---|---|
| Töölisi | 2 | 1 | 0 | 3 | 2 |
Õige vastus on: C.
Tähistame töölisi lühiduse mõttes tähtedega: olgu Anna A, Bruno B ja Carmen C.
Alustame sellest, et teeme selgeks, millised kaks töölist saavad töötada esmaspäeval. Paarid võiksid olla A-B, A-C ja B-C. Võime välistada paari A-B, kuna 2. reegli kohaselt läheb koos B-ga tööle ka C, aga esmaspäeval ei tohtinud tööl olla kolme inimest. Seega alustame kahe variandiga: A-C ja B-C.
Variant 1:
| Esmaspäev | Teisipäev | Kolmapäev | Neljapäev | Reede | |
|---|---|---|---|---|---|
| Tööl | A-C | ? | ? | ? | ? |
| Kodus | B | B | ? | ? | ? |
Variant 2:
| Esmaspäev | Teisipäev | Kolmapäev | Neljapäev | Reede | |
|---|---|---|---|---|---|
| Tööl | B-C | ? | ? | ? | ? |
| Kodus | A | C | A | ? | ? |
Esimese variandi puhul ei tohi vastavalt 1. reeglile teisipäeval töötada B, 2. variandi puhul ei tohi vastavalt 2. reeglile teisipäeval töötada C. Nii saame vastusevariantidest välistada A.
Teise variandi puhul näeme ka reeglit 3: A jääb koju peale C kojujäämist. Seega kui on mingi päev, kus keegi tööle ei lähe, siis sellele järgmisel päeval ei saa kõik 3 uuesti tööl olla, kuna A peab jääma koju. Nii välistame vastusevariandi D.
Ajagraafik B vastab reeglitele ainult kuni kolmapäevani: võime alustada variandist 1 (esmaspäeval töötavad A ja C), C võib töötada teisipäeval ja kõik võivad tööle minna kolmapäeval:
| Esmaspäev | Teisipäev | Kolmapäev | Neljapäev | Reede | |
|---|---|---|---|---|---|
| Tööl | A-C | C | A-B-C | ? | ? |
| Kodus | B | A-B | - | B-C | A |
Kui aga kõik töötavad kolmapäeval, siis peavad nii B kui C jääma neljapäeval koju (vastavalt reeglid 1 ja 2), ainult A saab sel juhul neljapäeval töötada. Seega peame välistama ka vastusevariandi B.
Ainuke sobiv variant on C, järgnev tabel vastab kõigile reeglitele:
| Esmaspäev | Teisipäev | Kolmapäev | Neljapäev | Reede | |
|---|---|---|---|---|---|
| Tööl | A-C | C | A-B-C | A | - |
| Kodus | B | A-B | - | B-C | A-B-C |
Selle ülesande puhul võib rakendada erinevaid strateegiaid. Toodud seletuses lõime me hüpoteesi (näiteks "A ja B töötavad esmaspäeval") ja kontrollime sammhaaval, kas see on võimalik toodud reeglite põhjal (kas see rahuldab meie tingimusi). Kui jah, läheme ühe sammu edasi ja kontrollime tulemust jne. Kui leiame mingil momendil vastuolu, astume sammu tagasi, loome uue hüpoteesi ja proovime seda samal moel kontrollida.
Inimese jaoks on raske pidevalt jälgida, et hüpoteeside tegemine oleks süstemaatiline ja et võimalik lahendus kindlasti leitakse. Heaks näiteks on sudoku lahendamine: mida raskem sudoku, seda rohkem peame looma (ja seda tõenäolisemalt ka kummutama) hüpoteese. Arvutiprogrammid suudavad olla seevastu väga süstemaatilised ning seetõttu on loodud palju algoritme analoogsete ülesannete lahendamiseks.
Kobraste kuningas otsustas rahvuspüha suurejooneliselt tähistada ning lasi keskväljakule tuua valguspaneelid, et nende abil mustreid luua. Valguspaneele oli kokku 36, neist igaüht võis peale astudes lülitada kas sisse või välja. Kuningas alustab paneelist, mis on tähistatud kirjaga IN, seejärel liigub igalt paneelilt selle naabrile (üleval, all, vasakul või paremal, kuid mitte diagonaalis) ja lõpetab paneelil kirjaga OUT, luues nii erinevaid helendavaid mustreid. Ta võib ühele paneelile astuda ka rohkem kui ühe korra.
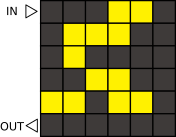
Kuningas tegi esmalt ülaltoodud mustri (kus kollased ruudud tähistavad helendavaid, hallid aga välja lülitatud paneele). Kuna talle see muster ei meeldinud, tahtis ta kõik paneelid taas sisse lülitada ja uuesti alustada.
Milline alltoodud marsruutidest lülitab kõik paneelid uuesti sisse?
[Raadionupud]
A.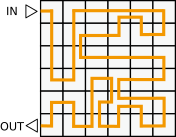 
B.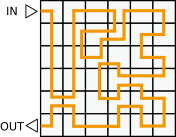 
C.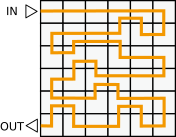 
D.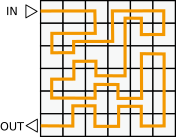 
Õige vastus on: C.
Vaja on valida marsruut, mille puhul astutakse algselt helendavatele paneelidele kaks korda ja algselt välja lülitatud paneelidele ühe korra. Alloleval joonisel on iga marsruudi kohta punaselt näidatud paneelid, millele astutakse kaks korda.
Programmeerimises on oluline jälgida tegevuse tulemust. Momendil tuleb vaadata iga paneeli puhul, milline on tema lõppolek marsruudi läbimisel. Kuna tegemist on töömahuka ülesandega, peab vastusevariante kitsendamise abil välistama.
Tabelarvutussüsteemis tähistatakse esimest 26 veergu ladina (täpsemalt küll inglise) tähestiku tähtedega:
Järgmist 26 veergu tähistatakse 2-täheliste kombinatsioonidega AA kuni AZ:
Nende järel järgmist 26 kombinatsioonidega BA kuni BZ:
Nii jätkub see, kuni kahetähelised kombinatsioonid ZZ järel otsa saavad. Siis alustatakse kolmetähelistega AAA kuni AAZ:
Milline on 2020. veeru tähis?
Kirjuta 3-täheline vastus (ainult tähed A-Z).
[Tekstikast]
Õige vastus on: BYR.
Üks võimalus vastuse leidmiseks on avada tabelarvutusprogramm, panna kursor töölehe esimesse veergu, vajutada 2019 korda klahvi "nool paremale" ja vaadata siis vastava veeru tähis. See on muidugi tüütu ja lisaks on üsna suur risk, et vahepeal võib loendamine segi minna.
Teine võimalus on panna tähele, et
ühetäheliste tähistega on 26 veergu, ehk veerud 1 kuni 26;
kahetähelistes tähistes on võimalikke esitähti 26 ja iga esitähe järele teiseks täheks ka 26 võimalikku varianti; seega on kahetähelisi tähiseid kokku 26*26=676; seega on kahetäheliste tähistega veerud 27 kuni 702;
eelnevaga sarnase loogika põhjal on kolmetähelisi 262626=17576; seega on kolmetäheliste tähistega veerud 703 kuni 18278;
seega on 2020. veeru tähis kolmetäheline ja see on kolmetäheliste hulgas kohal 2020-702=1318;
kolmetäheliste tähiste hulgas on iga esitähega tähistes teiseks ja kolmandaks täheks kõik kahetähelised paarid; seega on iga algustähega kolmetäheliste plokis 676 tähist;
kuna 1 < 1318/676 ⩽ 2, siis peab otsitav veerg olema teises sellise plokis, ehk selle tähise esimene täht peab olema B;
B-tähega algavate kolmetäheliste hulgas on otsiva veeru koht 1318-1*676=642;
kolmetäheliste B-tähega algavate hulgas on igale teisele tähele vastavas plokis kolmandaks täheks kõik üksikud tähed; seega on igas sellises plokis 26 tähist;
kuna 24 < 642/26 ⩽ 25, peab otsitav veerg olema kahekümne viiendas sellises plokis, ehk selle tähise teine täht peab olema Y;
BY-paariga algavate kolmetäheliste hulgas on otsitava veeru koht 642-24*26=18, ehk selle kolmas täht peab olema R;
seega on 2020. veeru tähis BYR.
Arvutisüsteemides on alatasa vaja mitmesuguste objektide tähiseid erinevate esituste vahel teisendada. Kõike tavalisem näide on arvude teisendamine inimestele harjumuspärase kümnendsüsteemi ja arvutis sisemiselt kasutatava kahendsüsteemi vahel.
Näiteks kui me kirjutame 10-süsteemis 345, siis tähendab see avaldist
310^2 + 410^1 + 5*10^0 = 300+40+5 = 345.
Sama arvu esitus 2-süsteemis oleks 101011001, mis tähendab avaldist
12^8 + 02^7 + 12^6 + 02^5 + 12^4 + 12^3 + 02^3 + 02^1 + 1*2^0 = 256+64+16+8+1 = 345.
Tabeliveergude tähistes on kasutusel 26 "numbrit" A kuni Z, ja nii on meil tegemist 26-süsteemiga, kus iga järgmise järgu kaal on eelmise omast 26 korda suurem. Aga erinevalt klassikalisest positsioonilisest süsteemist, kus 26 numbri väärtused peaks olema 0 kuni 25, on tabeliveergude tähistamisel nende väärtusteks 1 kuni 26.
Seda tausta teades saaksime vastuse arvutada ka standardse algoritmiga, mille abil on võimalik leida mistahes arvu esitus mistahes positsioonilises arvusüsteemis:
2020 annab 26-ga jagamisel jäägi 18, seega peab otsitava tähise paremalt esimene märk olema R;
sellest kõrgemad järgud peavad andma kokku väärtuse (2020-18)/26=2002/26=77;
77 annab 26-ga jagamisel jäägi 25, seega peab otsitava tähise paremalt teine märk olema Y;
sellest kõrgemad järgud peavad andma kokku väärtuse (77-25)/26=52/26=2;
2 annab 26-ga jagamisel jäägi 2, seega peab otsitava tähise paremalt kolmas märk olema B;
sellest kõrgemad järgud peavad andma kokku väärtuse (2-2)/26=0/26=0 ja seega rohkem märke otsitavas tähises pole;
seega on 2020. veeru tähis BYR.
Ainuke erisus standardse algoritmiga võrreldes oleks reegel, et kui meil mingil hetkel annaks 26-ga jagamine jäägi 0, siis sellele jäägile vastavat märki meil pole ja me peaks selle asemel kasutama märki Z väärtusega 26. Ülesandes toodud näite puhul seda erisust ei teki, aga tabelitöötlusprogrammi veerutähiste arvutus peab muidugi sellega arvestama.
Kitsas parklas võivad autod teha järgmisi manöövreid:
Selleks, et punane auto pääseks parklast välja, on vaja manööverdada ka teiste autodega.
Milline on vähim kõigi autode manöövrite koguarv, et punane auto jõuaks punasele ruudule?
[Täisarv]
Õige vastus on: 11.
Punane auto saab parklast välja järgmise 11 manöövriga:
Nüüd on lisaks vaja veenduda, et 11 on tõesti vähim võimalik manöövrite arv.
Selleks kujutame esmalt ette, et punane auto on ainuke auto parklas. Siis peaks ta parklast välja saamiseks liikuma kokku 2 ruutu põhja suunas ja 3 ruutu ida suunas ja pöörama 2 korda. Ta võib teha neid manöövreid mitmes erinevas järjekorras, aga igal juhul tuleb tal teha vähemalt need 8 manöövrit.
Kuna parklas on ka teisi autosid, tuleb punase auto läbilaskmiseks neid ka liigutada.
Esmalt paneme tähele, et punase auto teed blokeerib allpool toodud L-kujuline kolmik. Nende vahele läbipääsu tekitamiseks piisab ühest manöövrist:
Edasi blokeerib punase auto teed järgmine L-kujuline kolmik. Nende vahele ühe manöövriga läbipääsu tekitada ei saa. Küll aga on see võimalik kahe manöövriga:
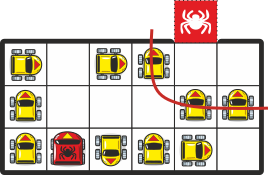
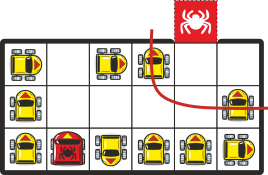
Seega ongi punase auto väljapääsemiseks vaja teha vähemalt 8+1+2 = 11 manöövrit.
See ülesanne kuulub optimeerimisülesannete hulka: meil on vaja ülesanne mitte lihtsalt lahendada, vaid teha seda mingi mõõdupuu järgi parimal võimalikul viisil. Sellistes ülesannetes on sageli kõige raskem osa just leitud lahenduse optimaalsuse tõestamine.
Paljudel juhtudel on ainus võimalus selleks kõigi variantide täielik läbivaatus (ingl exhaustive search): leiame kõik võimalikud lahendused ja näitame, et kõik teised on halvemad kui meie oma. Mõnelgi juhul võib kõigi variantide käsitsi kontrollimine olla liiga suur töö, aga arvutile jõukohane. Siiski on paljudes ülesannetes variantide arv nii suur, et nende kõigi kontrollimine võtaks ka arvutil liiga palju aega. Siis tuleb kasutada kas keerukamaid algoritme, nagu näiteks otsingupuu pügamist (ingl search tree pruning) või harude ja tõkete meetodit (ingl branch and bound) või iteratiivset süvendamist (ingl iterative deepening).
Mõnikord on aga võimalik leida ülesandes mingid erilised tingimused (nagu selles ülesandes L-kolmikud), mille abil võib lahenduse optimaalsust näidata ilma teisi variante läbi vaatamata. Mõnikord on need eritingimused ühe juhtumi spetsiifilised (näiteks kui kollased autod oleks paigutatud teisiti, ei tarvitseks L-kolmikute abil arutlemine sihile viia), mõnikord aga õnnestub leida üldised tingimused (nn invariandid), mis näitavad, et mingi ühe meetodi või süsteemi järgi koostatud lahendus on alati parim võimalik. Näiteks annab mõnes optimeerimisülesandes parima lahenduse nn ahne algoritm (ingl greedy algorithm), mis teeb igal sammul sel hetkel kõige kasulikumana tunduva käigu ilma mingit kaugemat strateegiat arvestamata.
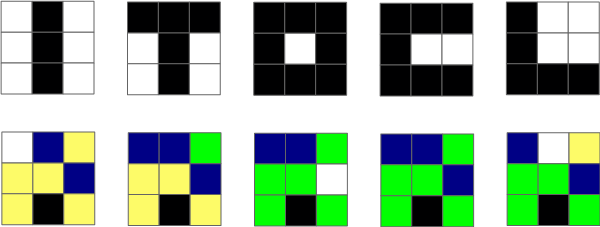
Kirjamasin suudab tuvastada viit pilti, mis kujutavad endast tähti I, T, O, C ja L.
Kirjamasin kasutab tuvastamisel nn. soojuskaarte. Pildi soojuskaardil näitab iga piksli (punkti) värv pildi vastava piksli värvi unikaalsust teiste piltide hulgas: mida unikaalsem on pildi piksli värv, seda heledam on piksel soojuskaardil.
Unikaalne: ühelgi teisel pildil pole selles kohas sama värvi pikslit.
Pigem unikaalne: ainult ühel teistest piltidest on selles kohas sama värvi piksel.
Pole unikaalne: kahel teistest piltidest on selles kohas sama värvi piksel.
Pigem tavaline: kolmel teistest piltidest on selles kohas sama värvi piksel.
Tavaline: kõigil piltidel on selles kohas sama värvi piksel.
Näiteks pildi 
soojuskaart on 
.
Millise pildi soojuskaart on 
?
[Raadionupud]
A. 
B. 
C. 
D. 
Õige vastus on: B.
Küsitaval soojuskaardil on 2. rea 3. veerus valge piksel. See tähendab, et see piksel on ühel tähel kõigist teistest erinev.
on ainuke pilt, millel on selles asukohas teistest erinev, täpsemalt must piksel; kõigil teistel piltidel on see piksel valge.
Siin on toodud kõik tähed koos neile vastavate soojuskaartidega:
Soojuskaart (ingl heat map) on andmete graafilise kujutamise üks viisidest, kus arvväärtused on asendatud värvikoodiga. Me oleme näinud selliseid kaarte näiteks ilmateadetes, kus värvidega tähistatakse erinevate piirkondade temperatuuri või sademete hulka.
Samuti kasutatakse soojuskaarti sarnaselt sellele ülesandele pildituvastuses, juhtides näiteks tehisnärvivõrkude treenimisel tähelepanu just teatud aladele pildil.
Kopraatias kasutatakse arvude märkimiseks ainult nulle ja ühtesid. Kaks Kopraatia last otsisid oma emale sünnipäevakingitust. Selleks oli neil kahe peale raha 11000101 kobrut. Lapsed leidsid kolm võimalikku kingitust: salli hinnaga 1110110 kobrut, kaelakee hinnaga 11001000 kobrut ja kella hinnaga 10011101 kobrut.
Milline on kõige kallim kingitus, mille lapsed saavad olemasoleva raha eest osta?
[Raadionupud]
A. Sall
B. Kaelakee
C. Kell
Õige vastus on: C (kell).
Antud kingitustest maksab kaelakee rohkem, kui on lastel raha: 11001000 > 11000101. Ülejäänud kahe asja jaoks on neil piisavalt raha: 1110110 < 11000101 ja 10011101 < 11000101. Seega saavad nad osta kas salli või kella. Neist kahest on kallim kell: 1110110 < 10011101.
Ülesanne on seotud kahendsüsteemiga. Kahendsüsteem kasutab erinevalt meie jaoks harjumuspärasest kümnendsüsteemist arvude märkimiseks vaid kaht numbrit: 0 ja 1. Kasutusel on ka teised arvusüsteemid, näiteks kaheksandsüsteem (numbrid 0-7) ja kuueteistkümnendsüsteem (numbrid 0-9 ning neile lisaks tähed A, B, C, D, E ja F).
Arvutid kasutavad kahendsüsteemi selle lihtsuse tõttu. Me võime mõelda numbrist 0 kui signaali puudumisest (lüliti on olekus "väljas") ja numbrist 1 kui signaali olemasolust (lüliti on olekus "sees"). Sel viisil saame lülitite erinevate olekute järgnevusena esitada suvalisi arve. Ka muud andmed (näiteks tähed) teisendatakse kahendarvudeks ja nii võib jada 01101000 tähistada kas arvu 104 või tähte "h".
Mati tahab avaldada kooli veebilehel õpilaste küsitluse tulemuste tulpdiagrammid. Kujundustarkvara võimaldab salvestada pilte mitmes vormingus.
Millist allolevatest vormingutest peaks diagrammide jaoks kasutama?
[Raadionupud]
Õige vastus on: D (PNG).
Pakutud variantidest on diagrammide veebis esitamiseks sobivaim vorming PNG. See on rastergraafika vorming, mis tähendab, et iga pilt esitatakse väikeste erivärviliste ruudukestena. PNG vorming kasutab kadudeta pakkimist, mis tähendab, et lahtipakkimisel saame tagasi täpselt esialgsed andmed. See vorming on sobiv suurte ühtlast värvi või korduva mustriga pindade ja kontrastsete joontega "kunstlike" jooniste esitamiseks, nagu diagrammid ongi. Ka on PNG vorming toetatud kõigis tänapäevastes veebilehitsejates nii arvuti- kui ka tahvli- ja telefoniopsüsteemides.
JPEG on samuti rastervorming, kuid kasutab kadudega pakkimist. JPEG on loodud, et esitada "naturaalseid" pilte, näiteks fotosid, kus on palju erinevaid toone ja sujuvaid üleminekuid nende vahel. Kontrastsete teravate joontega piltidel põhjustab selles vormingus kasutatav pakkimisalgoritm üsna suuri moonutusi, nagu näha allolevas võrdluses. Sellepärast ei ole see vorming kuigi sobiv "kunstlike" piltide (graafikud, joonised, erkaanitõmmised) jaoks.
BMP on kadudeta rastervoming, nagu ka PNG, kuid kasutab palju lihtsamat pakkimisalgoritmi, mistõttu on selles vormingus failid palju suuremad kui saaksime sama pilti PNG vormingus salvestades. Näiteks ühe umbes 600x350 pikseli suuruse tulpdiagrammi faili maht PNG vormingus on umbes 8 KB, aga BMP vormingus üle 600 KB. Lisaks on BMP Windowsi-spetsiifiline vorming ja ei tarvitse kõigi opsüsteemide veebilehitsejates toetatud olla.
EPS on kõigist eelnevatest erinevat vektorgraafika vorming. See tähendab, et EPS-failis kirjeldatakse pilti mitte ruudukujulistest pikselitest mosaiigina, vaid joontest, ristkülikutest, ringidest jmt geomeetrilistest objektidest koosnevana. Tänu sellele saab vektorvormingus pilte suurendada ja vähendada ilma, et nende kvaliteet sellest muutuks. Allolevas võrdlustabelis on näha, et PNG ja BMP vormingus pildid muutuvad suurenamisel ruuduliseks ning JPEG vormingus pilt läheb uduseks, aga vektorvormingus pilt jääb endiselt teravaks. EPS vormingu puudus on, et see on ajalooliselt trükitööstuses kasutusel olnud väga keeruline vorming ja ei ole veebilehitsejates toetatud (selles vormingus piltide vaatamiseks on vaja lisaprogrammi).
Tänapäevane ja ka veebis kasutamiseks mõeldud vektorgraafika vorming on Scalable Vector Graphics (*.svg). Sellel on üldiselt EPS vorminguga sarnased positiivsed omadused ja kui diagrammide koostamise tarkvara seda vormingut toetab, on see enamasti parim valik. Siiski tasub silmas pidada, et see on üsna uus ja veel arenev failivorming ning mõnede keerulisemate jooniste puhul võib juhtuda, et kõik veebilehitsejad ei oska neid päris õigesti näidata.
| PNG/BMP (suurendus) | JPEG (suurendus) | SVG/EPS (suurendus) |
|---|---|---|
 |
 |
 |
Kui samu andmeid on võimalik esitada mitmes erinevas vormingus, nagu see näiteks graafika puhul on, siis peab õige vormingu valimiseks teadma iga vormingu tugevaid ja nõrku külgi.
Copyright © 2020 Bebras – International Challenge on Informatics and Computational Thinking.
Licensed under Creative Commons Attribution-ShareAlike 4.0 International License.
Flag icons by GoSquared.