Мише подарили программируемое устройство с тремя лампочками: красная, зелёная и синяя. Первоначально все лампочки выключены, но с помощью программы их можно зажечь.
Небольшой пример из программы:
REPEAT: turn_on(RED_LED); wait(1s); turn_off(RED_LED); wait(2s);
Это программа действует следующим образом:
Миша нашёл в интернете новую программу и хочет её попробовать.
REPEAT: turn_on(BLUE_LED); wait(2s); turn_on(RED_LED); turn_on(GREEN_LED); wait(2s); turn_off(GREEN_LED); turn_off(BLUE_LED); wait(2s); turn_on(GREEN_LED); wait(2s); turn_off(RED_LED); turn_off(GREEN_LED);
Сколько лампочек будет гореть через 13 секунд после запуска этой программы?
[Täisarv [0, 3]]
Правильный ответ: 1.
Разобраться в ответе поможет диаграмма, где на временной шкале показаны графики горения трёх лампочек. Более высокое положение на каждом графике указывает на то, что лампочка горит, а более низкое положение на то, что она не горит. Как видно, через 13 секунд после запуска программы будет гореть красная лампочка, а зелёная и синяя нет.
При составлении такой диаграммы проще всего отдельно изучить состояние каждой лампочки. Например, для составления графика красной лампочки уберём из программы шаги, связанные с зелёной и синей лампочками:
REPEAT: wait(2s); turn_on(RED_LED); wait(2s); wait(2s); wait(2s); turn_off(RED_LED);
Теперь легко представить, каким будет график красной лампочки: 2 секунды не горит, 2+2+2=6 секунд горит, и далее опять всё с начало.
Аналогично составляется график для зелёной и синей лампочек.
Понимание программного кода является важным умением в информатике. В данном задании используется так называемый процедурный язык программирования. Схожий язык используется, например, в Arduino, ставшим очень популярным устройством при обучении программированию.
Здесь в задании необходимо понимать программу и симулировать её работу. Это очень важное действие для каждого программиста особенно тогда, когда необходимо найти причину, по которой программа работает не так, как ожидалось.
Зачастую при анализе сложных программ полезнее сосредоточиться разом на одном моменте работы программы. Этот подход использовался и в этом задании при анализе работы каждой из лампочек.
На болоте из пенёчков выложена дорожка. На ней бобры встретились с группой кенгуру, которые переходили болото таким же образом, что и бобры, но в противоположном направлении. Никто не хотел намочиться или запачкаться, поэтому все остались стоять на пенёчках. Рядом с дорожкой кенгуру заметили камень, на который можно перепрыгнуть с пенёчка и с которого можно вернуться на тот же пенёчек. Перепрыгнуть на камень могут только кенгуру и одновременно на камне может находиться только один из них.
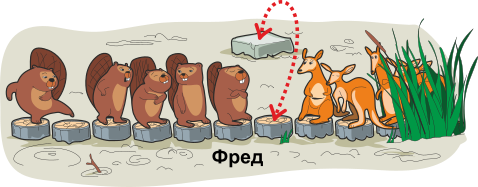
Ни бобры, ни кенгуру не имели ничего против того, чтобы двигаться и назад. Один только главный бобр Фред, который встретился с кенгуру первым, был согласен отступить в итоге только на 10 шагов назад.
Сколько кенгуру смогут обойти Фреда, учитывая его требования?
[Raadionupud]
A. Фреда смогут обойти больше, чем 10 кенгуру.
B. Фреда смогут обойти ровно 10 кенгуру.
C. Фреда смогут обойти ровно 6 кенгуру.
D. Фреда смогут обойти ровно 4 кенгуру.
E. Фреда смогут обойти меньше, чем 4 кенгуру.
F. На этот вопрос нельзя ответить.
Правильный ответ: C.
На секундочку мы можем забыть про других бобров, кроме Фреда. Если кенгуру хочет обойти Фреда, то для этого предпринимаются следующие шаги.
Кенгуру перепрыгивает на камень:
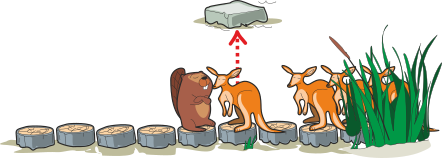
Фред идёт на два шага вперёд:
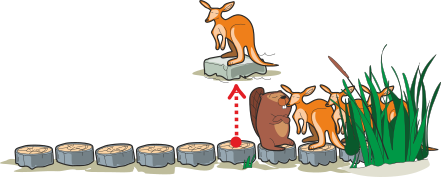
Кенгуру перепрыгивает обратно на дорожку и может продолжить путь:
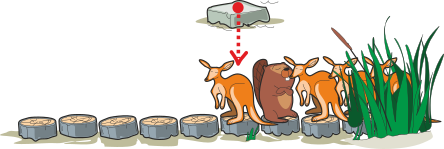
Фред возвращается на два шага назад, чтобы дать возможность следующему кенгуру перепрыгнуть на камень:
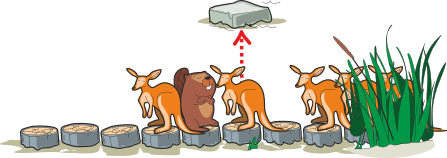
Если повторить эти шаги пять раз, то Фреда смогут обойти пять кенгуру, а сам бобр должен будет сделать в итоге десять шагов назад. Также и шестой кенгуру сможет обойти бобра, так как Фреду надо будет сделать 2 шага вперёд, чтобы пропустить кенгуру, но назад Фред уже не сможет шагнуть.
Решение мы можем записать и с помощью математического уравнения: если Фреда должны обойти K кенгуру, то он должен сделать S = 2 x (K – 1) шагов назад. Если это уравнение преобразуем для вычисления числа кенгуру, то получим K = S / 2 + 1.
Бобрёнок Юра играет с кубиками. Все кубики имеют одинаковую высоту, но ширина кубиков разная. Юра строит девять замечательных башен, каждая из которых построена из кубиков с одинаковой шириной.
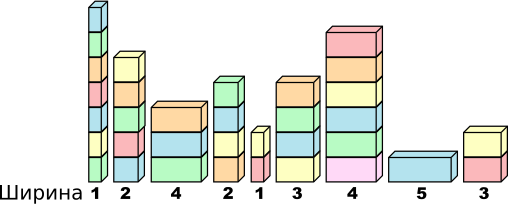
Для изменения высоты башни имеется две возможности: положить наверх ещё кубики или убрать их оттуда. В любом случае на это затратится энергия, которая зависит от ширины башни и количества убранных кубиков. Например, для того, чтобы удалить два кубика из башни шириной 1, понадобится 2x1=1 единица энергии, а для того, чтобы положить 4 кубика на верх башни шириной 3, понадобится 4x3=12 единиц энергии.
Юра хочет перестроить башни таким образом, чтобы они были одинаковой высоты и при этом затратить как можно меньше энергии.
Какое минимальное количество единиц энергии будет затрачено, чтобы все башни оказались одинаковой высоты?
[Täisarv [0, 100]]
Правильный ответ: 39.
Если обозначим добавление кубика с помощью символа 
, а удаление с помощью 
, то решение будет выглядеть следующим образом:
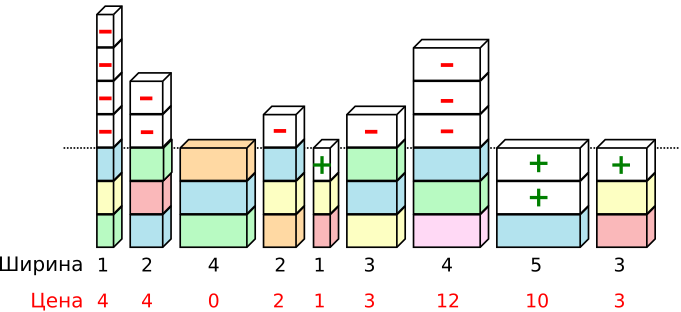
Медианная высота башен равна 4 (1 2 2 3 4 4 5 6 7) и можно считать, что выбор медианной высоты, как единой высоты для всех башен, является оптимальным. Однако в данном случае это не так. Проблема заключается в том, что кубики имеют разную ширину.
| Ширина | 1 | 2 | 4 | 2 | 1 | 3 | 4 | 5 | 3 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Первоначальная высота | 7 | 5 | 3 | 4 | 2 | 4 | 6 | 1 | 2 | Итого энергозатрат |
| Высота 1 | 6 | 8 | 8 | 6 | 1 | 9 | 20 | 0 | 3 | 61 |
| Высота 2 | 5 | 6 | 4 | 4 | 0 | 6 | 16 | 5 | 0 | 46 |
| Высота 3 | 4 | 4 | 0 | 2 | 1 | 3 | 12 | 10 | 3 | 39 |
| Высота 4 | 3 | 2 | 4 | 0 | 2 | 0 | 8 | 15 | 6 | 40 |
| Высота 5 | 2 | 0 | 8 | 2 | 3 | 3 | 4 | 20 | 9 | 51 |
| Высота 6 | 1 | 2 | 12 | 4 | 4 | 6 | 0 | 25 | 12 | 66 |
| Высота 7 | 0 | 4 | 16 | 6 | 5 | 9 | 4 | 30 | 15 | 89 |
В предыдущей таблице найдены энергозатраты для всех вариантов перестроек. Конечно, мы не должны рассматривать все варианты, потому что у энергозатрат есть один минимум. Можем начать, например, с медианной высоты 4 и сравнить эти энергозатраты с затратами на строительство башен высотой 3 и 5. Так как в случае высоты 3 затраты меньше, то минимум должен располагаться в ту сторону от 4. Если также сравним энергозатраты для высоты 2, то увидим, что они опять будут больше, чем затраты для высоты 3. Таким образом, 3 является оптимальной высотой.
Бобр Дима отправился на еженедельный рынок. Там он встретил двух других бобров, а именно бобров k1 и k2. В свою очередь бобры k1 и k2 тоже встретили двух бобров. Теперь было бы логично спросить, так сколько же бобров минимально должно было быть на рынке, чтобы каждый их них (бобры Дима, k1 и k2) смог встретиться с двумя бобрами?
Мы можем представить бобров и их встречи с помощью следующего рисунка:
В таком случае на рынке должно быть по меньшей мере пять бобров.
Однако возможны и другие варианты:
В этих случаях на рынке должно быть по меньшей мере 4 (рисунок слева) или 3 (рисунок справа) бобра. Таким образом, становится очевидным, что минимальное количество бобров на рынке должно быть 3.
На следующей неделе бобр Дима вновь отправился на рынок и встретил там трёх других бобров, которые в этот же день встретили соответственно двух, пять и пять бобров.
Сколько бобров минимально должно было быть на рынке в этот день?
[Täisarv [0, 15]]
Правильный ответ: 7.
Если мы посчитаем Диму и тех бобров, с кем он встретился (k1, k2 и k3), то получим в итоге 4 бобров.
Рассмотрим случай с бобром k1, который встретился с двумя бобрами. Нам необходимо найти самое маленькое количество бобров, поэтому мы должны предполагать, что k1 встретился с Димой и либо с k2, либо с k3. Если это так, то по-прежнему будет достаточно четырёх бобров.
Теперь рассмотрим случай с бобром k2, который встретился с пятью бобрами. Мы знаем, что он встретился с Димой и, возможно, с k1. Если мы предположим, что k2 встретился с k1 и k3, то должно быть по меньшей мере ещё два бобра k4 и k5, с которыми встретился k2. Таким образом, минимальное количество возрастает до шести.
Число 6 не может всё-таки быть конечным числом, потому что k1 встретился только с двумя бобрами, т.е. (помимо Димы) либо с k2, либо с k3 (или ни с одним из них двух). Так как мы предполагали, что k1 встретился с Димой и k2, то он не смог встретиться с k3. Таким образом, в возможном списке тех, с кем k3 мог встретиться, будут только Дима, k1, а также k4 и k5, с которым встретился и k2. Получается, что k3 должен встретиться ещё с одним "новым" бобром k6. Значит, итоговым ответом будет число 7.
Можем нарисовать граф с 7 вершинами, чтобы помочь решить проблему и доказать, что решение с 7ю бобрами является верным.
В этом задании для решения мы воспользовались графом. Граф состоит из вершин и соединяющих их рёбер. Графы могут быть неориентированными (между вершинами нет иерархии, а у рёбер направлений) или ориентированным (рёбрам присвоено направление).
В данном задании мы составляем граф: вершины обозначают бобров, а рёбра - это их встречи с другими бобрами. Это неориентированный граф, так как встречи происходят симметрично: если один бобр встречается с другим, то второй в то же самое время встречается тоже с первым. Ориентированный граф можно было бы использовать, например, в том случае, если бы бобры не встречались между собой, а, видели бы других: в этом случае один бобр мог видеть другого, но другой не обязательно бы видел первого.
Граф является мощным средством для представления сложных проблем простым способом. Например, графы используются при представлении сетей, будь то городские улицы, телефонные или электросети. Также в виде графа можем представить и социальные сети, например, LinkedIn или Facebook: в роли вершин выступают аккаунты с логином, именем, полом и другой информацией личности, а рёбра демонстрируют связи между аккаунтами.
У каждого живого существа имеется ДНК, которая определяет его гены. ДНК - это последовательность нуклеотидов, которых существует четыре разных типа: аденин (A), гуанин (G), цитозин (C) и тимин (T). ДНК может мутировать в новые последовательности, которые будут отличаться от оригинала.
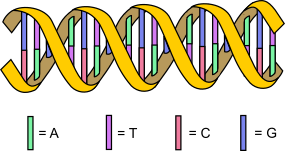
Бобрик - это существо, у которого ДНК может мутировать тремя способами:
Какая из этих последовательностей нуклеотидов НЕ МОЖЕТ быть ДНК бобрика после трёх мутаций, если первоначальное ДНК бобрика было GTATCG?
[Raadionupud]
A. GCAATG
B. ATTATCCG
C. GAATGC
D. GGTAAAC
Правильный ответ: D (GGTAAAC).
Вариант A: GTATCG - замещение (T на C) – GCATCG - замещение (T на A) – GCAACG - замещение (C на T) – GCAATG.
Вариант B: GTATCG - замещение (G на A) – ATATCG - дублирование (T) – ATTATCG - дублирование (C) – ATTATCCG.
Вариант C: GTATCG - замещение (T на A) – GAATCG - замещение (C на G) – GAATGG - замещение (G на C) – GAATGC.
Поэтому варианты A, B и C возможно получить за 3 шага мутации.
Но для получения варианта D необходимо сделать 4 шага: GTATCG - дублирование (G) - GGTATCG - дублирование (A) - GGTAATCG - замещение (T на A) - GGTAAACG - удаление (G) - GGTAAAC.
Для решения задания необходимо найти, на каком расстоянии от начала находится каждая конечная последовательность. Расстоянием будем считать число произошедших мутаций.
В принципе, для этого необходимо просмотреть все мутации первоначальной последовательности после одного шага; далее все те мутации, которые мы получим от ещё после одного шага (т.е. от первоначальной последовательности после двух шагов) и т.д. Объём бессмысленной работы можем уменьшить за счёт того, что, если в какой-то момент мы обнаружим ранее встречавшуюся нам последовательность, то мы не обратим на неё внимание (потому что нам уже известна более короткая дорога для получения этой последовательности от начала).
Такое расстояние, измеряемое шагами мутации, известно в компьютерных науках как расстояние Левенштейна. В его классическом проявлении при преобразовании одного текста в другой разрешёнными операциями являются добавление буквы, удаление буквы и замещение одной буквы другой. В нашем задании добавление буквы заменено дублированием нуклеотидов, но в разных приложение встречаются и другие вариации.
Бобры придумали набор паролей, чтобы защитить свои дома. Пароли состоят только из двух символов: 
и 
.
Контролёр пароля должен определиться, является ли он верным или неверным. Этот процесс иллюстрирует нижеприведённый рисунок:
В приведённом наверху примере верным паролем может считаться только такой:
Бобры создали нового контролёра пароля:
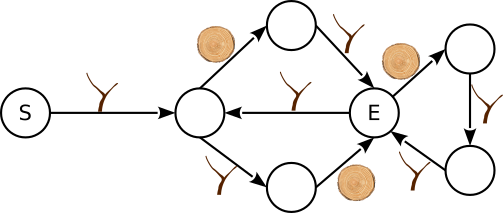
Бобры решили воспользоваться несколькими комплектами символов, чтобы создать пароли.
Из каких приведённых комплектов можно создать пароль, который будет принят контролёром пароля?
Необходимо использовать все имеющиеся в комплекте символы.
[Märkeruudud]
A. 4 x , 8 x
B. 2 x , 4 x
C. 5 x , 8 x
D. 5 x , 7 x
Правильный ответ: A и B.
Ответы A и B являются верными. Подходящие пароли содержат в два раза больше символов, чем символов.
Ответ C неверный: он состоит из 13 символов, а длина принятого пароля должна делиться на три.
Ответ D неверный: пароль содержал бы 7 символов и 5 символов , а подходящие пароли должны содержать в два раза больше символов, чем символов.
Контролёр паролей, разработанный бобрами, основывается на так называемом автомате (точнее, на детерминированном конечном автомате). Это математическая модель. Такой автомат может в каждый момент времени быть только в одном состоянии; состояние меняет приходящая со входа информация.
Автоматы применяются в различных устройствах для контроля очерёдности действий. Например, в торговых автоматах (различные шаги в процессе покупки), лифты (очерёдность остановок в соответствии с пожеланиями пользователя), светофоры (изменение режима, если машина стоит), кодовые замки (контроль последовательности введённых цифр) и т.д.
На заводе производятся различные изделия, которые во время производства проходят несколько заводских отделов. Весь производственный процесс можно проиллюстрировать с помощью схемы: прямоугольники обозначают отделы, а стрелки - перемещение изделии из одного отдела в другой.
Имеется два типа отделов: производственные отделы и упаковочные отделы.
или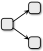 
.К производственному процессу применяются условия:
Какая из приведённых схем отображает соответствующий этим условиям производственный процесс?
[Raadionupud]
A.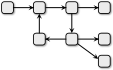 
B.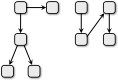 
C.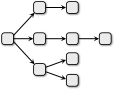 
D.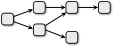 
E.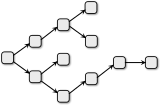 
Правильный ответ: E.
Вариант A является некорректным, потому что один отдел получит входной материал больше, чем из одного места, и один отдел отправит изделие больше, чем в два отдела.
Вариант B является некорректным, потому что имеется два отдела, которые не получат входной материал ни из одного другого отдела, а по условию таких отделов может быть только один.
Вариант C является некорректным, потому что один отдел отправит изделие больше, чем в два отдела.
Вариант D является некорректным, потому что один отдел получит входной материал больше, чем из одного места.
Вариант E является корректным, потому что имеется ровно один исходный отдел (который не получит входной материал из других отделов), каждый другой отдел получит входной материал только из одного места; к тому же ни один отдел не отправит изделие больше, чем в два отдела.
В информатике такие схемы называют графами. Граф - это структура данных, который используется для представления объектов и связей между ними. В данном случае в роли объектов выступают отделы, а стрелки между отделами обозначают прохождение изделия из одного отдела в другой. В информатике графы очень часто используются в разных ситуациях, например, при разработке сетей. Абстрактное представление практических ситуаций позволяет применить один алгоритм при решение многих различных прикладных задач.
В данном задании описанные условия производственного процесса определяют, что описывающий процесс граф должен быть деревом: он - связный (из исходного отдела, перемещаясь по стрелочкам, можно попасть в любой другой отдел) и в нём нет циклов (стартуя из любого из отделов и перемещаясь по стрелочкам, нельзя попасть обратно в то же место). Такие графы позволяют представить иерархические отношения - например, родословное дерево, где, двигаясь по стрелочкам, можно от расположенной в центре личности дойти до его прародителей.
Робот работает на длинной узкой дорожке. Дорожка разделена на пронумерованные квадраты, которых бесконечно много:
Предмет находится на одном из пронумерованных квадратов, и робот может его перемещать в соответствии с определёнными командами. После выполнения команды робот больше не помнит первоначальное местоположение предмета.
Робот получает команды ВЫПОЛНИ и ОТМЕНИ. Если робот получает команду "ВЫПОЛНИ правило 1", то он перемещает предмет в соответствии с правилом 1. Если робот получает команду "ОТМЕНИ правило 1", то он должен восстановить положение, которое было до применения правила 1. Команду ОТМЕНИ можно использовать только непосредственно после содержащей то же правило команды ВЫПОЛНИ. Однако не все правила можно отменить.
Допустим, у нас имеется два правила:
Если робот получит команду "ВЫПОЛНИ правило 1", то он переместит предмет на один квадрат правее. Для выполнения команды "ОТМЕНИ правило 1" будет достаточно того, что предмет будет перемещён на один квадрат левее и, таким образом, правило 1 будет отменено.
Если робот получит команду "ВЫПОЛНИ правило 2", то он переместит предмет на первый квадрат. Так как после этого робот больше не помнит, на каком квадрате до этого был предмет, то правило 2 не является отменяемым.
Какие из следующих правил являются отменяемыми?
[Märkeruudud]
A. Если предмет находится на квадрате, номер которого больше 8, то перенеси предмет на один квадрат правее; в противном случае оставь предмет на том же квадрате.
B. Если предмет находится на квадрате, номер которого больше 8, то перенеси предмет на один квадрат левее; в противном случае оставь предмет на том же квадрате.
C. Если предмет находится на обозначенном чётным числом квадрате, то перенеси предмет на два квадрата правее; в противном случае перенеси на один квадрат левее.
D. Если предмет находится на обозначенном чётным числом квадрате, то перенеси предмет на два квадрата правее; в противном случае перенеси на два квадрата левее.
Правильный ответ: A и D.
При применении правила A к предметам, расположенным на различных квадратах, получим следующие результаты:
Если предмет находился на квадрате, номер которого больше 8, то номер его нового местоположения будет больше 9 (синие стрелки). Если номер его первоначального местоположения был 8 или меньше, то предмет остался на том же квадрате (красные стрелки). Таким образом, эти два случая легко различимы, и отмену правила А можно было бы записать как "Если предмет находится на квадрате, номер которого больше 9, то перенеси его на один квадрат левее; в противном случае оставь предмет на том же месте".
При применении правила D получим следующие результаты:
Если до этого предмет был на квадрате с чётным числом, то и теперь он будет находиться на обозначенном чётным числом квадрате (синие стрелки); если же этот предмет был на квадрате с нечётным числом, то и в конце он будет находиться на квадрате с нечётным числом. Здесь также можно различить эти два случая и отмену правила D можно было бы записать как "Если предмет находится на обозначенном чётным числом квадрате, то перенеси его на два квадрата левее; в противном случае на два квадрата правее".
Теперь посмотрим, почему другие правила не являются отменяемыми.
При применении правила В получим следующие результаты:
Если предмет был на квадрате 8, то он и остался на этом квадрате (красная стрелка). Если предмет был на квадрате 9, то его перенесли на один квадрат левее, т.е. на квадрат 8 (синяя стрелка). Поэтому после применения правила нельзя будет сказать, что расположенный на квадрате 8 предмет был до этого на этом же квадрате или переместился сюда с квадрата 9. По этой причине правило B и не является отменяемым.
При применении правила С получим следующие результаты:
Если до этого предмет был на квадрате с чётным числом, то и теперь он находится на обозначенном чётным числом квадрате (синие стрелки); если же этот предмет был на квадрате с нечётным числом, то и в конце он будет находится на квадрате с нечётным числом (красные стрелки). Поэтому и здесь нельзя однозначно решить, на каком квадрате до этого находился предмет. Таким образом, и правило С не является отменяемым.
Анна, Вова и Света являются единственными тремя работниками на заводе. Они ходят на работу по точно установленным правилам. Каждый понедельник на работе должно быть ровно два работника, в другие же дни в соответствии со следующими правилами:
Для оптимизации производства в разные дни может потребоваться различное количество работников. Какой из приведённых ниже недельных планов возможен при соблюдении ранее описанных требований?
[Raadionupud]
| Понедельник | Вторник | Среда | Четверг | Пятница | |
|---|---|---|---|---|---|
| Работники | 2 | 3 | 1 | 1 | 2 |
| Понедельник | Вторник | Среда | Четверг | Пятница | |
|---|---|---|---|---|---|
| Работники | 2 | 1 | 3 | 2 | 1 |
| Понедельник | Вторник | Среда | Четверг | Пятница | |
|---|---|---|---|---|---|
| Работники | 2 | 1 | 3 | 1 | 0 |
| Понедельник | Вторник | Среда | Четверг | Пятница | |
|---|---|---|---|---|---|
| Работники | 2 | 1 | 0 | 3 | 2 |
Правильный ответ: C.
Обозначим для краткости работников следующими буквами: пускай Анна будет A, Вова B и Света C.
Начнём с того, что выясним, кто эти два работника, которые смогут работать в понедельник. Возможны пары A-B, A-C и B-C. Пару A-B можем исключить, потому что по условию правила 2 вместе с B на работу пойдёт и C, но в понедельник на работе не должно быть трёх человек. Поэтому начнём сразу с вариантов: A-C и B-C.
Вариант 1:
| Понедельник | Вторник | Среда | Четверг | Пятница | |
|---|---|---|---|---|---|
| На работе | A-C | ? | ? | ? | ? |
| Дома | B | B | ? | ? | ? |
Вариант 2:
| Понедельник | Вторник | Среда | Четверг | Пятница | |
|---|---|---|---|---|---|
| На работе | B-C | ? | ? | ? | ? |
| Дома | A | C | A | ? | ? |
В первом варианте по условию правила 1 во вторник на работе не может находиться B. Во втором варианте по условию правила 2 во вторник не может находиться C. Таким образом, из вариантов ответов можем исключить A.
Во втором случае видим и правило 3: A останется дома после того, как C осталась дома. Поэтому, если существует какой-то день, в который никто не пойдёт на работу, то в последующий ему день на работу не могут пойти все 3 работника, потому что А должна остаться дома. Таким образом, из вариантов ответов можем исключить D.
Вариант графика работ B соответствует требованиям только до среды: можем начать с варианта 1 (в понедельник работают A и C), C может работать во вторник, и все могут выйти на работу в среду:
| Понедельник | Вторник | Среда | Четверг | Пятница | |
|---|---|---|---|---|---|
| На работе | A-C | C | A-B-C | ? | ? |
| Дома | B | A-B | - | B-C | A |
Если все будут работать в среду, то B и C должны остаться в четверг дома (в соответствии с правилами 1 и 2), в таком случае в четверг сможет работать только A. Таким образом, из вариантов ответов можем исключить B.
Единственным подходящим вариантом будет C, следующая таблица соответствует всем правилам:
| Понедельник | Вторник | Среда | Четверг | Пятница | |
|---|---|---|---|---|---|
| На работе | A-C | C | A-B-C | A | - |
| Дома | B | A-B | - | B-C | A-B-C |
Для решения этого задания можно применять различные стратегии. В приведённом объяснении мы выдвинули гипотезу (например, "A и B работают в понедельник") и пошагово проверяем, возможно ли это на основании приведённых правил (удовлетворяет ли это нашим условиям). Если да, то переходим к следующему шагу и проверяем результат, и т.д. Если в какой-то момент заметим противоречие, то вернёмся на один шаг назад, выдвинем новую гипотезу и попробуем её проверить таким же образом.
Для человека очень трудно постоянно следить, чтобы выдвижение гипотез было бы систематичным и чтобы возможное решение обязательно было бы найденным. Хорошим примером является решение судоку: чем труднее судоку, тем больше гипотез должны выдвигать (и тем вероятнее их опровергать). Компьютерные программы в этом отношении очень систематичны, и поэтому создано много различных алгоритмов для решения аналогичных заданий.
Король бобров решил грандиозно отменить национальный праздник и приказал на центральной площади установить создающие разные узоры световые панели. Всего было установлено 36 панелей, и, наступив на каждую из них, её можно было включить или выключить. Король начал с панели, которая обозначена IN, далее он двигался с каждой панели на соседнюю (наверх, вниз, влево, вправо, но не по диагонали) и закончил на панели, которая обозначена OUT. Таким образом он создал различные светящиеся узоры. Он мог на одну и ту же панель наступать больше одного раза.
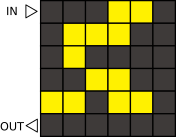
Сначала король создал приведённый наверху узор (где жёлтые квадраты обозначают светящиеся, а серые - выключенные панели). Однако этот узор ему не понравился, и он захотел вновь включить все панели и начать заново.
Какой из приведённых маршрутов вновь включит все панели?
[Raadionupud]
A.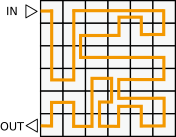 
B.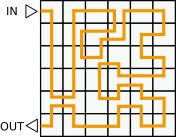 
C.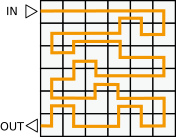 
D. 
Правильный ответ: C.
Необходимо выбрать маршрут, где король два раза наступает на первоначально светящиеся панели и один раз на первоначально выключенные панели. На приведённом ниже рисунке для каждого маршрута красным отмечены панели, на которые он наступает два раза.
В программировании важно следить за результатом действия. В данный момент для каждой панели необходимо смотреть, каково будет её конечное состояние после прохождения маршрута. Так как это трудоёмкое задание, то варианты ответов надо исключать с помощью ограничений.
В системах электронных таблиц первые 26 столбцов обозначены буквами латинского (вернее английского) алфавита:
Следующие 26 столбцов обозначены двухбуквенными комбинациями от AA до AZ:
Следующие за ними последующие 26 столбцов обозначены комбинациями от BA до BZ:
Так продолжается до тех пор, пока не закончатся двухбуквенные комбинации после ZZ. После этого начинают использовать трёхбуквенные комбинации от AAA до AAZ:
Какое обозначение имеет 2020-ый столбец?
Напиши трёхзначный ответ (только буквы A-Z).
[Tekstikast]
Правильный ответ: BYR.
Одним из способов решить это задание является помощь программы электронных таблиц - откроем её, установим курсор в самый первый столбец рабочего листа, 2019 раз нажмём на клавишу "стрелка вправо" и посмотрим, какое обозначение будет у соответствующего столбца. Это, конечно, нудно, и к тому же существует большой риск того, что мы можем в какой-то момент сбиться со счёта.
Другая возможность - это обратить внимание на то, что
с однобуквенными обозначениями имеется 26 столбцов, то есть столбцы от 1 до 26;
в двухбуквенных обозначениях для первой буквы имеется 26 вариантов, для каждой следующей за первой буквой второй буквы имеется также 26 возможных вариантов; таким образом, всего двухбуквенных обозначений будет 26*26=676; получаем, что столбцы с двухбуквенными обозначениями будут от 27 до 702;
по аналогии с применённой в прошлом пункте логикой трёхбуквенных обозначений будет 262626=17576; таким образом, столбцы с трёхбуквенными обозначениями будут от 703 до 18278;
получаем, что обозначение 2020-ого столбца должно быть трёхбуквенным и среди трёхбуквенных он будет на 2020-702=1318 месте;
в числе трёхбуквенных обозначений после каждой уникальной первой буквы в качестве второй и третьей букв могут быть использованы все возможные двухбуквенные пары; таким образом, для каждой первой буквы в трёхбуквенном блоке может быть 676 обозначений;
так как 1 < 1318/676 ⩽ 2, то искомый столбец должен быть во втором таком блоке, т.е. первой буквой этого обозначения должна быть B;
в числе начинающихся на букву B трехбуквенных обозначениях место искомого столбца будет 1318-1*676=642;
в числе начинающихся на букву B трехбуквенных обозначениях после каждой второй буквы третьей буквой может быть любая одиночная буква; таким образом, в этом блоке будет 26 обозначений;
так как 24 < 642/26 ⩽ 25, то искомый столбец должен быть в двадцать пятом таком блоке, т.е. второй буквой этого обозначения должна быть Y;
в числе трёхбуквенном обозначений, начинающихся с пары BY, место искомого столбца будет 642-24*26=18, т.е. третьей буквой должна быть R;
таким образом, обозначением 2020-ого столбца является BYR.
В вычислительных системах постоянно необходимо преобразовывать обозначения различных объектов. Самым обычным примером можно считать преобразование привычной для человека десятичной системы в двоичную систему, используемую компьютерами.
Например, если в 10-ой системе запишем 345, то это обозначает выражение
310^2 + 410^1 + 5*10^0 = 300+40+5 = 345.
Представление этого же числа в 2-ой системе было бы 101011001, и выражение было бы
12^8 + 02^7 + 12^6 + 02^5 + 12^4 + 12^3 + 02^3 + 02^1 + 1*2^0 = 256+64+16+8+1 = 345.
В обозначении столбцов таблицы использовано 26 "цифр" от A до Z и, таким образом, у нас используется 26-ая система, где доля каждого следующего разряда в 26 раз больше доли предыдущего разряда. Однако в отличие от классической позиционной системы счисления, где значения 26 цифр могут быть от 0 до 25, в обозначение столбцов их значения могут быть от 1 до 26.
Зная эту особенность, ответ можно рассчитать и с помощью стандартного алгоритма, который позволяет найти представление любого числа в любой позиционной системе счисления:
при делении 2020 на 26 получается остаток 18; таким образом, в искомом обозначении первым символом справа должен быть R;
старшие разряды в итоге должны дать значение (2020-18)/26=2002/26=77;
при делении 77 на 26 получаем остаток 25; таким образом, в искомом обозначении вторым символом справа должен быть Y;
старшие разряды в итоге должны дать значение (77-25)/26=52/26=2;
при делении 2 на 26 получаем остаток 2; таким образом, в искомом обозначении третьим символом справа должен быть B;
старшие разряды в итоге должны дать значение (2-2)/26=0/26=0, и поэтому в искомом обозначении символов больше нет;
таким образом, обозначением 2020-ого столбца является BYR.
Единственным отличием от стандартного алгоритма было бы правило, согласно которому, если в какой-то момент при делении на 26 у нас получился бы остаток 0, то у нас нет соответствующего остатку символа, и вместо этого мы должны были бы использовать символ Z со значением 26. В случае приведённого в задании примера такой особенности не возникло, но при вычислении обозначений столбцов в программе электронных таблиц, конечно, следует это учитывать.
На узкой стоянке машины могут выполнять следующие манёвры:
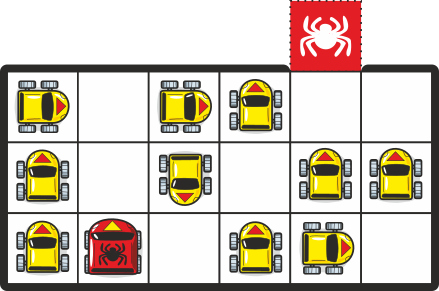
Для того, чтобы красная машина смогла выехать с парковки, потребуется перемещение и других машин.
Какое наименьшее общее количество манёвров потребуется от всех машин, чтобы красная машина смогла добраться до красного квадрата?
[Täisarv]
Правильный ответ: 11.
Красная машина сможет выехать с парковки за следующие 11 манёвров:
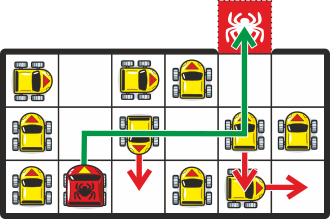
Теперь необходимо убедиться, что 11 является действительно наименьшим возможным количеством манёвров.
Прежде всего, представим себе, что красная машина - это единственная машина на парковке. В таком случае для того, чтобы выехать с парковки, необходимо проехать 2 квадрата в направлении севера и 3 квадрата в направлении востока, а также совершить 2 поворота. Машина может сделать эти манёвры в разных последовательностях, но в любом случае необходимо сделать все 8 манёвров.
Так как на парковке имеются и другие машины, то для проезда красной машины их также необходимо переместить.
Прежде всего, проезд красной машине блокируют три машины, выставленные в форме L. Чтобы проехать этот участок, достаточно будет сделать один манёвр:
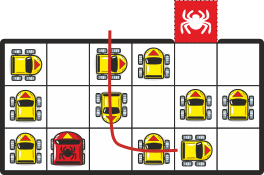
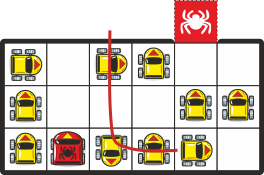
Далее проезд красной машине блокируют следующие три машины, выставленные в форме L. Разблокировать этот участок за один манёвр не получится, но за два можно:
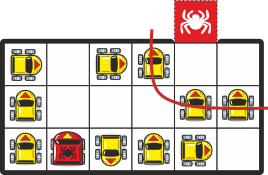
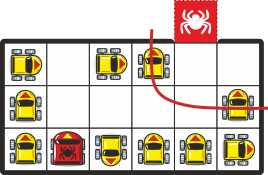
Таким образом, чтобы красная машина смогла выехать с парковки, необходимо сделать 8+1+2 = 11 манёвров.
Это задание относится к числу заданий на оптимизацию: нам надо не просто решить задание, а решить его наилучшим возможным способом. В таких заданиях самой трудной частью зачастую является доказательство оптимальности найденного решения.
Во многих случаях единственной возможностью для этого является просмотр всех возможных вариантов (англ exhaustive search): найдём все возможные решения и покажем, что все другие будут хуже, чем наше решение. В некоторых случаях проверка всех вариантов вручную является очень большой работой, но она посильна компьютерам. Однако во многих заданиях количество возможных вариантов настолько велико, что их проверка даже с помощью компьютера заняла бы слишком много времени. В таких случаях следует воспользоваться сложными алгоритмами, такими как обрезка дерева поиска (ingl search tree pruning) или метод ветвей и границ (ingl branch and bound), или итеративное углубление (ingl iterative deepening).
Иногда в задании можно найти некоторые особые условия (как например в этом задании три машины, выставленные в форме L), с помощью которых оптимальность решения можно показать без изучения других вариантов. Случается, что эти особые условия являются специфическими для одного конкретного случая (например, если бы жёлтые машины были расположены по-другому, то рассуждение про три машины, выставленные в форме L, не привели бы к желаемому результату), а иногда удаётся найти общие условия (так называемые инварианты), которые показывают, что с помощью одного метода или системы составленное решение является наилучшим возможным. Например, в некоторых заданиях на оптимизацию лучшее решение можно получить с помощью так называемого жадного алгоритма (англ greedy algorithm), который на каждом этапе совершает кажущийся самым полезным шаг без учёта какой-нибудь далеко идущей стратегии.
Печатная машинка может распознать пять картинок, которые представляют собой буквы I, T, O, C и L.
Для распознавания печатная машинка использует так называемые тепловые карты. Цвет каждого пикселя (точки) на тепловой карте картинки указывает на уникальность использованного в этом месте картинки цвета по отношению к другим картинкам: чем уникальнее цвет пикселя картинки, тем светлее будет пиксель на тепловой карте.
Уникальный: ни на одной другой картинке в этом месте нет пикселя с таким же цветом.
Скорее уникальный: только на одной из других картинок в этом же месте имеется пиксель того же цвета.
Не уникальный: на двух других картинках в этом же месте имеется пиксель того же цвета.
Скорее обычный: на трёх других картинках в этом же месте имеется пиксель того же цвета.
Обычный: на всех картинках в этом же месте имеется пиксель того же цвета.
Например, картинке 
соответствует тепловая карта 
.
Какой картинке соответствует тепловая карта 
?
[Raadionupud]
A. 
B. 
C. 
D. 
Правильный ответ: B.
На изучаемой тепловой карте во втором ряду третьего столбца имеется белый пиксель. Это означает, что этот пиксель на одной из букв отличается от всех остальных.
является единственной картинкой, у которой в этом месте имеется отличающийся от всех других картинок чёрный пиксель; на всех других картинках этот пиксель имеет белый цвет.
Далее приведены все буквы с соответствующими им тепловыми картами:
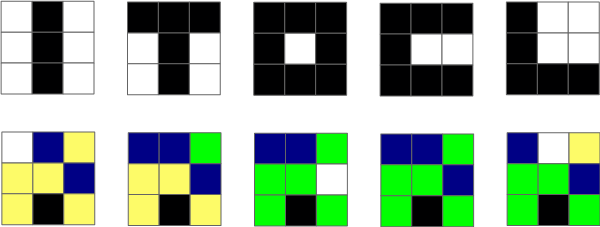
Тепловые карты (англ heat map) являются одной из форм графического представления данных, где числовые значения заменены на цветовой код. Такие карты мы могли наблюдать в сообщениях о погоде, где с помощью цвета обозначают температуру или количество осадков в разных районах.
Аналогично данному заданию тепловые карты также используются при распознавание фотографии, где, например, с при тренировке искусственной нейронной сети обращается внимание на определённые области фотографии.
В Бобруйске для обозначения чисел используются только нули и единицы. Два бобрёнка решили найти подарок маме на день рождения. На двоих у них было 11000101 бобриков денег. Дети нашли три возможных подарка: шарф стоимостью 1110110 бобрика, ожерелье стоимостью 11001000 бобрика и часы стоимостью 10011101 бобрика.
Какой самый дорогой подарок смогут приобрести дети на имеющиеся у них деньги?
[Raadionupud]
A. Шарф
B. Ожерелье
C. Часы
Правильный ответ: C (часы).
Из имеющихся подарков ожерелье стоит больше, чем есть денег у детей: 11001000 > 11000101. Для оставшихся вещей у них имеется достаточное количество денег: 1110110 < 11000101 и 10011101 < 11000101. Таким образом, они могут купить шарф или часы. Из них двоих самыми дорогими будут часы: 1110110 < 10011101.
Задание связано с двоичной системой. В двоичной системе, в отличие от привычной для нас десятичной системы, для обозначения чисел используются только две цифры: 0 и 1. Существуют и другие системы счисления. Например, восьмеричная система (цифры 0-7) или шестнадцатеричная система (цифры 0-9 и в дополнении к ним буквы A, B, C, D, E и F).
Компьютеры используют двоичную систему из-за её простоты. Мы можем представить цифру 0 как отсутствие сигнала (выключатель в положении "выкл") и цифру 1 как наличие сигнала (выключатель в положении "вкл"). Таким образом, благодаря различным последовательностям состояний, мы можем записать различные числа. В двоичные числа можно преобразовать и другие данные (например, буквы) - последовательность 01101000 может обозначать число 104 или букву "h".
Митя хочет опубликовать на сайте школы диаграммы результатов опроса учеников. Графический редактор позволяет сохранять изображения в различных форматах.
Какой из следующих форматов следует использовать для диаграмм?
[Raadionupud]
A. Windows Bitmap (*.bmp)
B. Encapsulated PostScript (*.eps)
C. Joint Picture Experts Group image format (*.jpg)
D. Portable Network Graphics (*.png)
Правильный ответ: D (PNG).
Для публикации диаграммы в Интернете из предложенных вариантов лучше всего подходит формат PNG. Это формат растровой графики, где каждая картинка представлена в виде маленьких разноцветных квадратиков. PNG формат основывается на сжатии без потерь. Это означает, что при восстановлении получим точно такие же первоначальные данные. Данный формат очень подходит для представления "искусственных" рисунков, состоящих из больших участков с однородным цветом или повторяющимся узором, или имеющих контрастные линии. Именно так и выглядят диаграммы. Также PNG формат поддерживается всеми современными браузерами, которые доступны в операционных системах для настольных компьютеров, планшетов и телефонов.
JPEG также является растровым форматом, но сжатие происходит с потерями. JPEG был создан для того, чтобы представлять "естественные" рисунки, как, например, фотографии, где много различных тонов и плавных переходов между ними. Если для сохранения рисунков с контрастными чёткими линиями использовать этот формат, то применяемый алгоритм сжатия приведёт к довольно большим искажениям (это видно на приведённом ниже сравнении). По этой причине этот формат не очень подходит для "искусственных" рисунков (графиков, чертежей, скриншотов).
BMP является растровым форматом без потерь, как и PNG, но основывается на более простых алгоритмах сжатия и поэтому сохранённые в этом формате файлы имеют больший размер, чем при сохранении точно такого же рисунка в формате PNG. Например, размер файла с одной примерно 600х350 пиксельной столбчатой диаграммой в формате PNG будет около 8 KB, а в формате BMP более 600 KB. Стоит учитывать, что BMP является форматом, специфичным для Windows, и поэтому не обязательно будет поддержан в браузерах других операционных систем.
EPS отличается от всех вышеописанных форматов, потому что это формат векторной графики. Это означает, что имеющиеся в EPS-файле рисунки описываются не с помощью мозаики из пикселей квадратной формы, а с помощью объектов, состоящих из геометрических фигур (линий, прямоугольников, кругов и др.). Благодаря этому рисунки в векторном формате можно увеличивать и уменьшать без изменения качества. В приведённой ниже сравнительной таблице видно, что при увеличении представленных в формате PNG и BMP рисунков они становятся квадратоподобными, а в случае JPEG формата рисунок становится нечётким. В то же время рисунок в векторном формате остаётся чётким. Недостатком EPS формата является то, что он исторически был очень сложным форматом, применявшимся в типографии, и сейчас не поддерживается браузерами (для просмотра рисунков в этом формате необходима отдельная программа).
Scalable Vector Graphics (*.svg) является современным форматом векторной графики и предназначен для использования в Интернете. У этого формата в общем схожие с EPS форматом позитивные свойства и, если программное обеспечения для создания диаграмм поддерживает этот формат, предпочтительнее использовать именно его. Однако стоит иметь ввиду, что это довольно новый и находящийся ещё в процессе развития файловый формат, поэтому в случае некоторых сложных рисунков может получиться так, что все браузеры не смогут их достоверно отобразить.
| PNG/BMP (увеличение) | JPEG (увеличение) | SVG/EPS (увеличение) |
|---|---|---|
 |
 |
 |
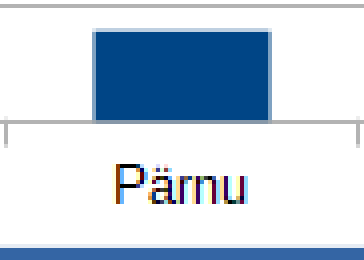Если одни и те же данные можно представить в разных форматах, как это, например, и есть в случае графики, то при выборе правильного формата надо знать его позитивные и негативные стороны.
Copyright © 2020 Bebras – International Challenge on Informatics and Computational Thinking.
Licensed under Creative Commons Attribution-ShareAlike 4.0 International License.
Flag icons by GoSquared.