

Nõial on kahte liiki jooke, X ja Y. Kui ta valab kahe pudeli sisu patta ja ütleb võlusõna, siis muudab jook värvi järgmiselt:

Nõid segas kokku täpselt 4 pudeli sisud teatavas järjekorras. Lõppsegu oli liiki Y  . Millises järjekorras ta pudelite sisud kokku segas?
. Millises järjekorras ta pudelite sisud kokku segas?
[Raadionupud]
A. 
B. 
C. 
D. 
Õige vastus on C.
Segades joogid antud järjekorras, saame järgmised tulemused.
A. 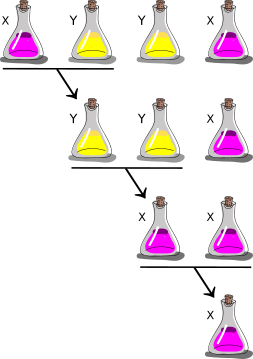
B. 
C. 
D. 
Et arvuti on elektrooniline masin, siis kasutatakse seal informatsiooni esitamiseks elektrit. Kui elekter pääseb läbi, siis ütleme, et elekter on SEES. Kui elekter läbi ei pääse, siis ütleme, et elekter on VÄLJAS. Arvutiteadlased tähistavad neid kahte olekut tavaliselt arvudega 1 ja 0. Seda nimetatakse kahendesituseks.
Üks ühik informatsiooni on bitt. Bitte võime omavahel kombineerida ja teha nendega tehteid, nagu nõid segab kokku jooke ning saab tulemuse. Üks neist tehetest on "välistav või" (XOR). See töötab järgmiselt:
0 XOR 0 = 0
0 XOR 1 = 1
1 XOR 0 = 1
1 XOR 1 = 0
Näide igapäevasest kasutusest: trepi otstes on lülitid, mis lülitavad ühte ja sama lampi. Kumbki lüliti lülitab lampi sisse ja välja. Kui üks lüliti on ülemises ja teine alumises asendis, siis lamp põleb. Kui mõlemad lülitid on ülemises asendis, siis lamp ei põle, ning kui mõlemad lülitid on alumises asendis, siis samuti lamp ei põle.
Teine näide: ema ütles, et ma peaks võtma lõunaks kaasa puuvilja. Lõunasöögipakis on ruumi ainult ühe puuvilja jaoks. Laual on õun ja apelsin. Kui ma ei võta midagi, siis ma ei täida ema soovi. Kui ma võtan nii õuna kui ka apelsini, siis need ei mahu korraga lõunasöögipakki. Seetõttu pean lõunasöögipakki panemiseks valima õuna ja apelsini vahel.
XOR-lüli on arvutis kasutatav loogikaelement. See lüli annab väljundiks 1 (tõene), kui täpselt üks sisenditest on 1 (tõene). Kui mõlemad sisendid on samad, siis on väljund 0 (väär).
XOR-tehte abil saab tuvastada ja parandada vigu. XOR-tehtel põhineb õppematerjalide kogumiku CSUnPlugged tegevus "Party magic".
XOR-tehte abil saab ka leida võitva strateegia mängu nim jaoks. Mängu alguses on laotud tikud mitmesse kuhja. Kaks mängijat võtavad vaheldumisi ühest valitud kuhjast suvalise (nullist erineva) arvu tikke. Võidab mängija, kes võtab viimase tiku. Võitev strateegia on muuta oma igal käigul mängu nim-summa (kuhjade suuruste kahend-XOR-summa) nulliks.
Arvutiteaduses on XOR-tehtel veel mitmeid rakendusi:

Linna siluett koosneb 14 tornist:

Kui tornid järjestada madalaimast kõrgeimani, siis milline torn on selles järjestuses 10. kohal?
[Raadionupud]
A. 
B. 
C. 
D. 
Õige vastus on B.
Vastuse leidmiseks paneme kõigepealt tähele, et torn, mis on madalaimast kõrgeima suunas järjestuses 10. kohal, on kõrgeimast madalaima suunas järjestuses 5. kohal. Seega on kasulikum lahendada ülesannet just sedapidi: nii jõuame vastuseni väiksema sammude arvuga.
Edasi paneme tähele, et siluett koosneb kahest tornide jadast: vasakpoolne, mis muutub kõrgemaks vasakult paremale, ning parempoolne, mis muutub kõrgemaks samuti vasakult paremale. Näeme, et mõlema jada kaks viimast torni on üleüldse neli kõige kõrgemat torni. Kõrguse poolest järgmine torn on vastusevariant B ning see ongi otsitav vastus.
Selles ülesandes palutakse sul määrata, milline torn asub tornide jadas 10. kohal, kui kõik tornid kõrguse järgi järjestada. Elementide järjekorda panemist nimetatakse sortimiseks.
Sortimisalgoritme tuntakse palju. See ülesanne seostub ühildusmeetodi nimelise algoritmiga (merge sort). Ühildusmeetodi põhiidee on sortida kaks elemendihulga poolt eraldi. Seejärel tuleb need kaks sorditud jada ühildada ning moodustada ühine sorditud jada. Kui siin antud ülesanne lahendada kõigi 14 torni sortimise teel, siis tuleb vasaku poole sorditud tornid ühildada parema poole sorditud tornidega.

Bianka on mägironija. Tema lemmik-mäeahelik koosneb 11 mäest:

Kui Bianka kõrval on kõrgem mägi, siis ronib ta alati kõrgema mäe otsa. Kui tema kõrval on kaks mäge (üks vasakul, üks paremal) ja üks neist on teisest kõrgem, siis ronib ta alati selle mäe otsa, mis on kõrgem. Seda jätkab ta seni, kuni tema kõrval enam kõrgemat mäge ei ole.
Mitu mäge (kõige kõrgem mägi ise sealhulgas) on sellised, et sealt alustades jõuab Bianka mäeaheliku kõige kõrgema mäe otsa?
[Raadionupud]
A. 3
B. 4
C. 6
D. 7
Õige vastus on A.
Kui Bianka alustab kõige kõrgema mäe otsast, jääb ta sinna. Kui Bianka alustab kõige kõrgema mäe kõrval olevast mäest, siis ronib ta kohe järgmisena kõige kõrgema mäe otsa ja jääb sinna. Seega kui arvestada ka kõige kõrgemat mäge, siis on vähemalt kolm mäge, millest alustades jõuab Bianka kõige kõrgema mäe otsa, nagu näidatud alloleval joonisel roheliste nooltega.

Kui Bianka alustab kaugemalt vasakult, siis ei pääse ta mööda kõrguselt kolmandast mäest, nagu näidatud joonisel vasakpoolsete punaste nooltega.
Kui Bianka alustab kaugemalt paremalt, jääb ta pidama kõrguselt teise mäe otsa, nagu näidatud joonisel parempoolsete punaste nooltega.
Järelikult ongi täpselt kolm mäge, millest alustades jõuab Bianka aheliku kõige kõrgema mäe otsa.
Protsessi, mida Bianka järgib, nimetatakse ahneks algoritmiks (greedy algorithm). Idee seisneb selles, et püüdes jõuda kõige kõrgema mäe tippu, valib ta järgmist sammu tehes ainult kahe naabermäe vahel. Selle asemel, et püüda leida globaalset maksimumi, otsib ta lokaalset maksimumi.
Ahned algoritmid ei lahenda alati ülesannet õigesti, aga juhul, kui nad seda teevad, töötavad nad tavaliselt väga efektiivselt. Seetõttu pakuvad ülesanded, millele saab ahneid algoritme rakendada, arvutiteadlastele suurt huvi. Aga ka siis, kui ahne algoritmi tulemus ei ole õige, saab selle algoritmi abil sageli leida lahendi, mis on "piisavalt hea". Seda nimetatakse lähendavaks algoritmiks (approximation algorithm).
Tehisintellektis kasutatakse erilist liiki ahnet algoritmi, mida nimetatakse mägironija algoritmiks (hill climbing algorithm). Nimi tuleneb ideest, millel põhineb käesolev ülesanne.
Selles ülesandes vaadeldav olukord seostub topograafilise eraldatuse mõistega geograafias. Informaatika on suurepärane selle poolest, et teda saab rakendada peaaegu igas ainevaldkonnas.

Olivia mängib klotsidega. Igale klotsile on kirjutatud üks number. Olivia ehitab klotsidest torni ja seejärel tõstab klotsid ühekaupa maha ning moodustab nendest arvu. Iga kord, kui ta klotsi maha tõstab, võib ta selle panna moodustatava arvu vasakuks või paremaks numbriks.
Järgmisel joonisel on kujutatud 4 klotsiga torn ja näidetena kaks võimalikku arvu, mida sellest moodustada saab (2534 ja 4235).


Mis on kõige väiksem arv, mille saab nende reeglite abil moodustada järgmisest 6 klotsi kõrgusest tornist?

[Tekstikast, täisarv]
Õige vastus on 347565.
Kõige väiksem võimalik arv peab algama torni kõige väiksema numbriga, milleks on 3. Selleks, et 3 jääks arvu esimeseks numbriks, tuleb kõik numbrid, mis asuvad tornis 3 all, lisada arvu paremasse otsa, seega arvu lõpus on 65.
Numbrist 3 ülespoole jääb väiksem torn 547, millest peame moodustama kõige väiksema arvu 3 ja 65 vahele. Arutleme samamoodi: arv peab algama kõige väiksema numbriga, milleks on 4, ja 5 tuleb lisada paremale. Seega saame arvu 475.
See annabki meile lõppvastuse: 475, mille ees on 3 ja järel 65, ehk kokku 347565.
Parima lahendi (nagu vähima arvu) otsimine kõigi võimaluste hulgast on väga levinud arvutuslik ülesanne, mida tuntakse optimeerimise nime all. Võimaluste hulga vähendamiseks ja otsingu kiirendamiseks kasutame sageli täiendavaid tehnikaid. Käesoleval juhul kasutame kõige vasakpoolsema numbri määramiseks ahnet strateegiat. Seejärel lahendame samasuguse väiksema ülesande kõige väiksema numbri kohal asuvate klotside jaoks jaga-ja-valitse strateegia abil.

Meil on salajane sõnum, mis on saadud ladina tähestiku tähtede kodeerimisel uute märkidega.
Kodeerimisviisi kirjeldus on tahvlil. Kahjuks aga on osa tahvli sisust maha pühitud:

Hoolimata sellest, et tahvel on kahjustada saanud, leia esialgne tekst, mis vastab järgnevale salakirjale:

[Raadionupud]
A. INFORMATION SECRET
B. INFORMATICS IS COOL
C. MATHEMATICS IS COOL
D. INFORMATION IS COOL
Õige vastus on B. INFORMATICS IS COOL.
Täielik krüptimistabel on:

Ülesande lahendamiseks tuleb aru saada, et uued märgid on moodustatud rea- ja veerutähiste järgi. Iga märgi alumine osa on rea tähis ning ülemine osa veeru tähis.
Puuduvad tähestiku tähed saab lihtsasti taastada, vaja on ainult teada ladina tähestiku tähtede järjekorda. Puudub ainult esimese rea tähis. Vaadeldes krüptitud teksti, saab teada, kuidas näeb välja puuduv alumine osa.
Mõnede ladina tähestiku tähe jaoks on salamärgid juba teada. Paigutades need krüptitud teksti, saame kätte osa esialgsest tekstist. Katsetades saaksime täita ka ülejäänud lüngad, kuid valikvastustega ülesandes pole see isegi vajalik.
Nimelt saab ülesannet lahendada ka ilma tabelit taastamata. Piisab tähele panna, et esimene märk vastab tähele I, mis välistab vastusevariandi C. Üheteistkümnes märk vastab tähele S, aga vastusevariantides A ja D on sellel kohal täht N. Seega ainuke võimalik vastusevariant nende nelja hulgas on B.
Andmete kaitsmise ülesanne on rohkem kui 4000 aastat vana. Krüptograafia on informaatika oluline osa, mis keskendub salakirjade loomisele konfidentsiaalsete andmete või sõnumite kaitsmiseks.
Vanades kultuurides oli salakirjade arendamisel peamiseks eesmärgiks lihtne lahtikrüptimisviis, mille sai pähe õppida. Käesoleva ülesande salakiri on loodud küll Kopra-viktoriini jaoks, aga see on liigi poolest just selline.
See on lihtne asendusšiffer (substitution cipher), milles tähestiku tähtede ja neid kodeerivate märkide vahel on üksühene vastavus.

Kopraraamatukogus on palju koprakeelseid raamatuid. Raamatukogus on raamatute hoidmiseks 10 kappi ning igas kapis on 10 riiulit. Kopraraamatukogu omistab igale raamatule erilise numbri, mis näitab raamatu asukohta, et raamatu saaks kiiresti üles leida. Iga raamatu eriline number on määratud raamatu pealkirjas olevate kopratähtede järgi vastavalt järgmisele tabelile:

Näiteks kui raamatu pealkiri on  , siis selle raamatu eriline number on 56432:
, siis selle raamatu eriline number on 56432:

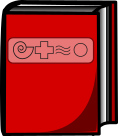
Millisel järgmistest raamatutest on sama eriline number nagu sellel punasel raamatul?
[Raadionupud]
A. 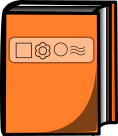
B. 
C. 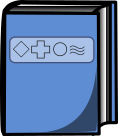
D. 
Õige vastus on C.
Leiame kõigepealt punase raamatu erilise numbri:
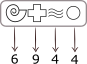
Seejärel leiame iga antud raamatu numbri ja teeme kindlaks, millise raamatu number on 6944:
A. 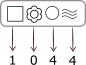
B. 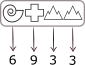
C. 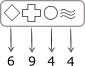
D. 
Näeme, et ainult vastusevariandis C antud raamatu number on 6944.
Informaatikas kasutatakse sagedasti vajaminevate andmete salvestamiseks andmestruktuuri, mille nimi on paisktabel. Andmeüksuse asukohta näitab paisktabelis indekskood, mida nimetatakse võtmeks (tavaliselt on selleks koodiks arv). Selles ülesandes luuakse sellised võtmed iga raamatu jaoks vastavustabeli meetodil. Ent nagu ülesandes näha, võib sama võti vastata mitmele raamatule. Seda olukorda nimetatakse põrkeks. Paisktabeli võtmete genereerimise meetodi loomisel peavad arvutiteadlased arvestama põrgete tekkimise võimalusega ja mõtlema välja viisi nendega toimetulemiseks.

Kobras Ann saadab salakoodide abil sõpradele sõnumeid. Praegu korraldab ta salajast pidu ja soovib saata oma sõpradele sissepääsuks vajaliku parooli 3124.
Ta uuristas ühe oma sõbra jaoks parooli viiele pulgale, aga pulkade järjekord läks sassi:
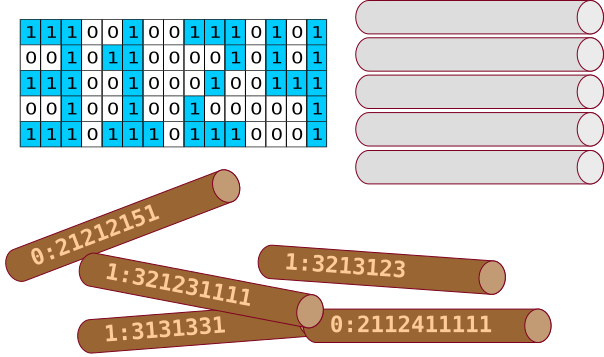
Millises järjekorras peaksid pulgad olema, ülevalt alla?
[Lohistamine]





Õige vastus on
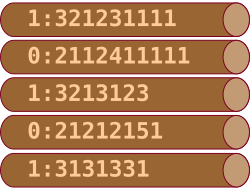
Iga pulk kirjeldab kompaktselt ühte kahendesituses kirja pandud sõnumi rida. Iga pulga esimene number näitab, kas rida algab valge või sinise ruuduga (0 tähistab valget ja 1 sinist). Kooloni järel tulevad numbrid näitavad, mitu ühte värvi ruutu kummastki vahelduvast värvist järgneb.
Näiteks ülesande joonisel algab esimene rida sinise ruuduga (1). Koolonile järgneb arv, mis näitab seda värvi ruutude arvu (3 sinist ruutu). Sellele järgneb 2 valget ruutu, siis 1 sinine ruut, siis 2 valget ruutu jne:

Seega peaks esimesel (ülemisel) pulgal olema järgmine kood:
| esimene ruut sinine | : | 3s | 2v | 1s | 2v | 3s | 1v | 1s | 1v | 1s |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | : | 3 | 2 | 1 | 2 | 3 | 1 | 1 | 1 | 1 |
Sõnumi teine rida algab valge ruuduga, seega teise pulga esimene number on 0. On 2 valget ruutu, millele järgneb 1 sinine ruut, 1 valge ruut, 2 sinist ruutu jne:

Seega on sellele vastav kood:
| esimene ruut valge | : | 2v | 1s | 1v | 2s | 4v | 1s | 1v | 1s | 1v | 1s |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | : | 2 | 1 | 1 | 2 | 4 | 1 | 1 | 1 | 1 | 1 |
Samamoodi saab sõnumi ridadele vastavusse seada kolm ülejäänud pulka.
Ülesanne toob sisse järjest mitu andmete kodeerimisega seotud mõistet:
Andmete töötlemise puhul on tavaline, et meil on sama informatsiooni esitamiseks mitu viisi ja vaja on teisendada andmeid ühest esitusest teise.
Selles ülesandes sisse toodud sarikodeerimine (run-length encoding, RLE) on kadudeta pakkimise väga lihtne vorm. Sarikodeerimise algoritmi rakendatakse jadadele, kus samu väärtusi esineb tihti mitu korda järjest. Selline jada kodeeritakse nii, et iga väärtus salvestatakse ainult üks kord, ning selle järele kirjutatakse selle esinemiskordade arv. Enamikel juhtudel tuleb väljundi suurus niimoodi sisendi suurusest väiksem, aga halvimal juhul võib see olla ka suurem.
Selles ülesandes on väärtuste salvestamisest loobutud, eeldades, et iga järgnev kordade arv vastab väärtusele, mis on eelmise väärtuse vastand. (Kas suudad leida näitejoonise, kus Ann sellise lähenemise tõttu raskustesse satub? Kas sellised joonised võivad esineda paroolide esitustena?)
Ülesande lahendamiseks on vaja üldistamise ja algoritmilise mõtlemise oskust. Esmalt peab tuletama sarikodeerimise algoritmi, võrreldes vastavaid ridu tabelis ja pulkadel. Seejärel peab rakendama seda algoritmi joonise ridadele ja saama kätte vastavad sõnumid.
Kodeeritud tulemusest joonise taastamine ja seejärel esituse sümbolite või numbrite kättesaamine ei ole inimese jaoks liiga raske. Kuid mida pikem on lause, seda rohkem aega ja jõudu on selleks vaja. Niisuguste ülesannete automatiseerimiseks arvutil tuleb välja mõtelda ja arvutile öelda, mida teha tuleb. Selleks ongi vaja arendada oma arvutusliku ja algoritmilise mõtlemise oskust.

Koprad Alar, Siim ja Erik seisavad kollasel ruudul oma kooli ees, näoga näidatud suunas.
Teel koju teeb igaüks neist teatavates kohtades pöörded.
Alar teeb kaks vasakpööret.
Siim teeb ühe vasakpöörde ja selle järel ühe parempöörde.
Erik teeb ühe vasakpöörde.
Iga kobras elab erinevas majas. Koprad liiguvad ainult horisontaalselt või vertikaalselt, aga mitte diagonaalselt. Koprad ei saa astuda hallidele ruutudele.
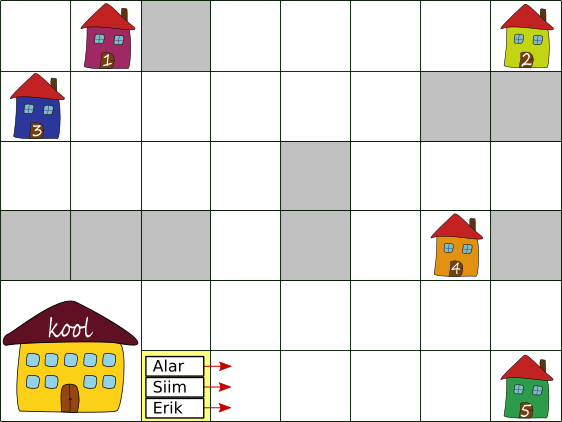
Millises majas iga kobras elab?
[Raadionupud]
A. Alar majas 4, Siim majas 2, Erik majas 5
B. Alar majas 3, Siim majas 2, Erik majas 1
C. Alar majas 4, Siim majas 2, Erik majas 1
D. Alar majas 3, Siim majas 2, Erik majas 4
Õige vastus on D.
Vastused A ja C on valed, sest majani 4 jõudmiseks tuleb kas pöörata üks kord vasakule või pöörata üks kord vasakule ja teine kord paremale või pöörata rohkem kui kaks korda. Seepärast ei saa Alar elada majas 4.
Vastus B on vale, sest majani 1 jõudmiseks tuleb pöörata kaks korda vasakule ja seejärel üks kord paremale. Seetõttu ei saa Erik elada majas 1.
Õige vastuseni jõudmiseks võib panna tähele, et maja 3 on ainuke maja, kuhu Alar jõuda saab. Siim saab jõuda majani 2 või 4, aga ta ei saa elada samas majas nagu Erik. Erik saab jõuda ainult majani 4.
Kujutada ette mingi tegevuse mõju pole tavaliselt liiga raske: kui on teada, et kobras on liikunud ruudustikul vasakule, vasakule ja paremale, siis on lihtne järgida tema liikumisi, eeldusel, et "vasakule" ja "paremale" on selgelt defineeritud tegevused, näiteks liikumine ühe ruudu võrra ruudustikus kopra hetkesuunaga määratud suunas. Ülesandes aga esitatakse raskem probleem, mis on informaatikas siiski üsna tavaline: antud on mõned tulemused või vihjed ning vaja on kindlaks teha, mis juhtus minevikus. Mitmel juhul on meil teada andmed (või isegi palju andmeid) ning me püüame aru saada, mis liiki protsessis need tekkinud on. Üldiselt võib samade andmetega kokku sobida mitu protsessi: näiteks on teada, et Siim pööras vasakule ja paremale, aga selle tingimusega on kooskõlas kaks erinevat maja (2 ja 4).

Koprad korraldasid maleturniiri. Nad on juba pidanud mõned mängud. Alloleval pildil on tõmmatud kõik nooled võitjatest kaotajateni. Näiteks Bruno võitis Aivit ja Aivi võitis Danielit.
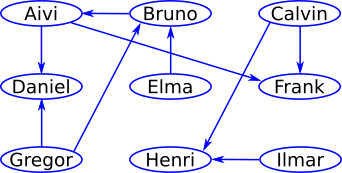
Et kobrastel ei olnud kõigi mängude pidamiseks aega, otsustasid nad võitja määrata uue reegli abil. Reegel on selline: kui Bruno võitis Aivit ja Aivi võitis Danielit, siis see tähendab, et Bruno võitis Danielit. Turniiri võitja on see, kes võitis selle reegli järgi iga ülejäänud kobrast.
Kuid tulemusi polnud võitja määramiseks piisavalt. Seetõttu otsustasid nad mängida veel neli mängu. Tulemused olid:

Kes võitis turniiri?
[Raadionupud]
A. Gregor
B. Ilmar
C. Calvin
D. Elma
Õige vastus on B. Ilmar.
Vastavalt reeglitele peab selleks, et turniiril oleks võitja, saama liikuda igast ülejäänud osalejast mööda nooli tagurpidi ühe ja sama osalejani. See tähendab, et täpselt ühel osalejal puuduvad sissetulevad nooled.
Kui selliseid osalejaid oleks rohkem kui üks, nagu esialgsel joonisel, siis on võitja määramiseks vaja rohkem mänge. Kui selliseid osalejaid üldse pole, siis ei saa reeglit rakendada.
Esimesel joonisel on ainult Gregor, Ilmar, Calvin ja Elma võimalikud võitjad.
Lisades neli viimast noolt, näeme, et Gregor ei saa olla võitja, sest ta kaotas Ilmarile. Calvin kaotas Gregorile ja Elma kaotas Henrile. Seega on Ilmar ainuke osaleja, kes võib olla võitja.
Alltoodud jooniselt näeme, et Ilmar tõepoolest võitis kõiki ülejäänud kopraid.
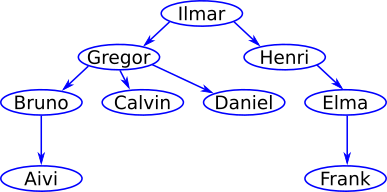
Suunatud graaf on viis, kuidas esitada (mittesümmeetrilisi) seoseid objektide paaride vahel: objekte kujutavad tipud ning objektist A viib nool objektini B siis, kui A on seoses B-ga.
Selles ülesandes on vaadeldavaks seoseks "võitja": mõned seosed tulevad tegelikult peetud kohtumistest, teised aga tekstis antud reeglist, mis ütleb, et võitmisseos on transitiivne. Spordis see tavaliselt nii ei ole. Spordimatše ongi huvitav jälgida just sellepärast et kui Bruno võidab Aivit ja Aivi võidab Danielit, siis see veel ei garanteeri, et Bruno võidab Danielit reaalses matšis. Ülesande olukord on aga tavaline informaatikas: mõnesid objekte ei saa vahetult ei võrrelda, aga siiski peame moodustama järjestuse, kus on võrreldud iga objektipaari.
Loomulikult võib selliseid järjestusi olla rohkem kui üks. Näiteks võivad meil olla tegevused või programmid, mis üksteisest sõltuvad: kingade jalgapanemiseks peab enne jalga panema sokid ning mantli selgapanemiseks peab enne selga panema särgi... aga kindlasti saad leida mitu erinevat viisi, kuidas oma riietumistegevused õigesti järjestada!

Järgmised käsud kirjeldavad kolmnurkade joonistamist:
joonista(üles, 1, 2)
|
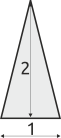
|
joonista(alla, 2, 1)
|
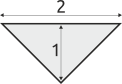
|
Pärast kujundi joonistamist asud samas kohas nagu alghetkel. Kui programmis on mitu käsku, täidetakse need järjest.
Meil on 4 programmi
joonista(alla, 2, 1); joonista(üles, 1, 2)
joonista(alla, 1, 2); joonista(üles, 2, 1)
joonista(alla, 2, 1); joonista(üles, 2, 1)
joonista(alla, 2, 1); joonista(üles, 1, 1)
Sea programmidele vastavusse pildid, mida need programmid joonistavad.
[Vastavusse seadmine]
A. 
B. 
C. 
D. 
programm vastab joonisele B. Kõigepealt joonistatakse "lame" kolmnurk tipuga allapoole ja seejärel "terav" kolmnurk tipuga ülespoole.
programm vastab joonisele A. Kõigepealt joonistatakse "terav" kolmnurk tipuga allapoole ja seejärel "lame" kolmnurk tipuga ülespoole.
programm vastab joonisele C. Joonistatakse kaks "lamedat" kolmnurka, üks tipuga ülespoole ja teine tipuga allapoole.
programm vastab joonisele D. Kõigepealt joonistatakse "lame" kolmnurk tipuga allapoole ja seejärel väiksem "terav" kolmnurk tipuga ülespoole.
Programmeerimises kasutame tavaliselt käske korduvalt, tehes neis väikesi muudatusi. Ülesandes on defineeritud joonistamisfunktsioon, millele on võimalik ette anda kolm parameetrit ja saadav joonis sõltub nende parameetrite väärtustest.
Meie (funktsiooni kasutaja) jaoks pole oluline, kuidas joonistamine töötab, me ei tea midagi selle "kehast" ehk sisemistest käskudest. Me ainult "kutsume" seda funktsiooni mitu korda erinevate väärtustega ja saame niimoodi joonistada erinevaid kolmnurki.

Bruno oli koolivaheajal kaks nädalat emal abiks nende kodukohvikus.
Iga tööpäeva õhtul märkis ta üles kassas oleva raha kogusumma ja sai sellise graafiku:
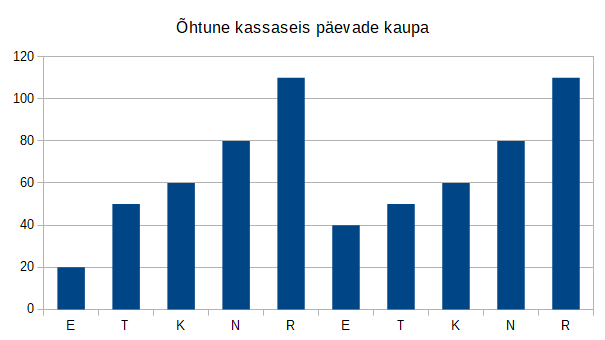
Mõlema reede õhtul võttis ta kassast kogu raha välja ja andis emale.
Mitu eurot oli kohviku suurim päevane sissetulek?
[Tekstikast, täisarv]
Õige vastus on 40€.
Kohviku käibest parema ülevaate saamiseks toome graafikul välja eraldi kassajäägi hommikul ja õhtul:
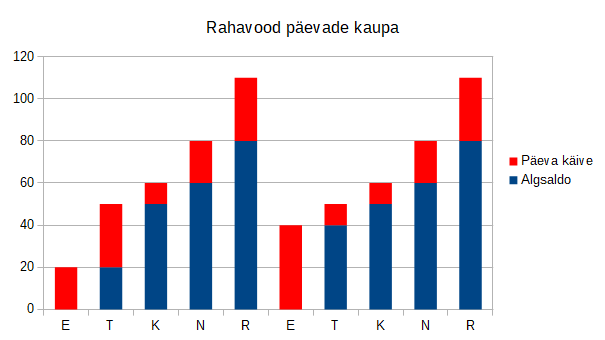
Veel selgem on asi, kui jätame graafikult välja hommikuse jäägi ja keskendume päeval lisandunud summale:
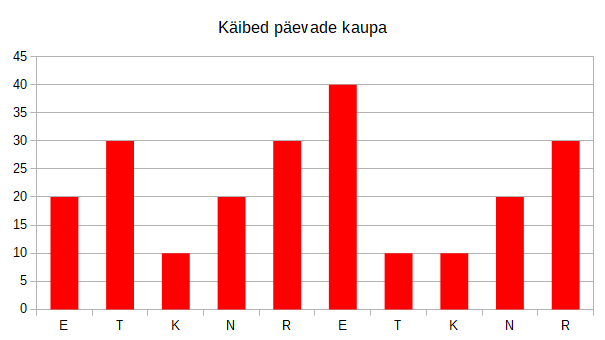
Nüüd on ilmne, et kõige suurema summa, 40€, teenis kohvik teise nädala esmaspäeval.
See ülesanne illustreerib, kuidas andmete esitusviis võib nende põhjal mõnele küsimusele vastamise teha kas lihtsamaks või keerulisemaks. Kui graafiku aluseks olevad andmed on arvutustabelis või andmebaasis, saab esituse parandamiseks vajaliku teisenduse lasta ära teha arvutil. Mida rohkem on andmeid, seda suurem on sellisest automaatsest parandamisest saadav kasu.

Järgnevas tekstis esineb sõna "beaver" viis korda:

Sõnade otsimisel ja asendamisel tekstitöötlusprogrammis võib lisaks sõnadele endile arvestada ka nende vormingut.
Mitu sõna "beaver" esinemist leitakse järgmise käsuga?

[Raadionupud]
A. 0
B. 3
C. 4
D. 5
Õige vastus on C. 4.
Kuna otsingutingimuseks on valitud lisaks sõnale "beaver" ka vorming "Italic" ehk kaldkiri, leitakse 4 esinemist:
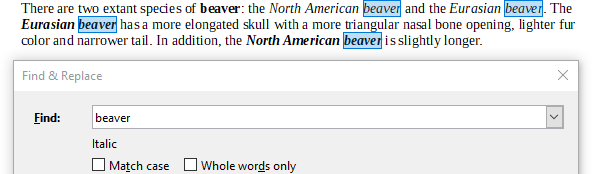
Tekstitöötlusprogrammi võimaluste tundmine ja nende kasutamine oma töö hõlbustamiseks on loomulikult informaatika!

Kobras Pfiffikus tahab moodustada parooli, mida tema suudab meeles pidada, aga mida keegi teine ei suuda lihtsasti ära arvata. Seetõttu kasutab ta parooli moodustamiseks erilist meetodit.

Kobras Pfiffikus armastab järgmist lauset:
Mulle meeldib puder mille valmistas kokk Wilhelm
Seepärast võtab ta selle lause oma parooli aluseks:
M5m7p5m5v9k4W7
Millise parooli saab samal meetodil moodustada sellisest lausest:
Minu robotiringi juhendaja on magister Hanna
[Tekstikast, vastuse pikkus 13 tähemärki]
Õige vastus on M4r11j9o2m8H5.
Kobras kasutab parooli moodustamiseks spetsiaalset meetodit. Selles meetodis võetakse igast sõnast esimene täht ja kirjutatakse selle järele sõna pikkus (tähtede arv sõnas).
Mulle → M5
meeldib → m7
puder → p5
mille → m5
valmistas → v9
kokk → k4
Wilhelm → W7
Kasutades sama meetodit, saame moodustada parooli ka uue lause põhjal:
Minu → M4
robotiringi → r11
juhendaja → j9
on → o2
magister → m8
Hanna → H5
Seega uue lause parool on M4r11j9o2m8H5.
Paneme tähele, et antud näites on tähed M ja W suurtähed. Kui mingi täht on suurtäht lauses, siis on ta suurtäht ka paroolis. Seepärast peavad vastuses samuti M ja H olema suurtähed.
Andmete turvalisus on informaatikas üks võtmeteemasid. Kõige lihtsam ja tavalisem lähenemine andmete ja arvutile juurdepääsu kaitsmisele on paroolide kasutamine.
Parool peab olema kergesti meeldejäetav, sest parooli üleskirjutamine on riskantne. Kuid parool peab olema teiste jaoks raskesti äraarvatav ning ei tohiks olla ilmne või seotud kasutaja isikuandmetega.

Minu arvuti loeb programme ridahaaval ülevalt alla.
Meil on selline programm:
A ← 2
Kirjuta A
A ← A*2
Kirjuta A
A ← A*2
Kirjuta A
A ← 100Märk ← tähendab "salvesta paremal poolel arvutatud väärtus muutujasse"; märk * tähendab korrutamist.
Kui see programm käima panna, siis kirjutab arvuti:
2
4
8Täna aga paistab, et minu arvutis on viirus, sest arvuti käitub imelikult. Ta loeb programme tagurpidi, alustades viimasest reast ja liikudes ülespoole.
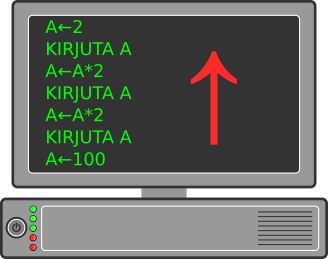
Mida minu viirusega arvuti kirjutas, kui see programm käima pandi?
[Raadionupud]
A.
8
4
2B.
100
50
25C.
2
4
8
100D.
100
200
400Õige vastus on D.
Kõigepealt järjestame read ümber, et saaksime neid lugeda ülevalt alla:
A ← 100
Kirjuta A
A ← A*2
Kirjuta A
A ← A*2
Kirjuta A
A ← 2Esimene täidetav käsk on seega A ← 100 ja teine käsk Kirjuta A. Seetõttu peab esimene kirjutatav arv olema 100.
Kui programmi ridu lugeda teises järjekorras, siis see ei tähenda, et käskudes sooritatakse teisi arvutusi. Käsk A ← A*2 ei tähenda tagurpidi lugedes käsku A ← A/2. Kui programm sisaldab ainult 2-ga korrutamise käske, siis peavad väärtused kasvama. Seega järgmised väärtused ei saa olla 50 ja 25.
Arvutiprogrammide lugemine on oluline oskus, sest me peame teadma, kuidas arvuti programmi ja seal olevaid käske täidab. Igal käsul on programmis õige koht, et programm töötaks õigesti. Programmeerijad peavad teadma, kuidas tulemused muutuvad, kui programmis käskude asukoht või järjestus muutub.

Kaks vangi, Jass ja Jonn kavatsevad alustada vanglast põgenemist esmaspäeval, 1. veebruaril. Vabadusse pääsemiseks tuleb neil kummalgi enne veebruari lõppu valmis kaevata käik, mis suundub 2 meetrit allapoole ja siis 30 meetrit edasi.

Tabelis on näidatud, mitu meetrit saavad nad igal nädalapäeval kaevata. Nädalalõpul nad kaevata ei saa.
| Esmaspäev | Teisipäev | Kolmapäev | Neljapäev | Reede | |
|---|---|---|---|---|---|
| Jass | 2 | 0 | 2 | 0 | 2 |
| Jonn | 0 | 4 | 0 | 4 | 0 |
Kellel on võimalik veebruari lõpus põgeneda?
[Raadionupud]
A. Mitte kummalgi
B. Ainult Jassil
C. Ainult Jonnil
D. Mõlemal vangil
Õige vastus on C.
Jooniselt on näha, et nad peavad kaevama ruumi põrandast 2 meetrit allapoole maa sisse ja seejärel 30 meetrit horisontaalselt, seega on neil edukaks põgenemiseks vaja kaevata 30+2=32 meetrit.
Põhiline on siin kuu "veebruar", sest veebruaris on 28 või 29 päeva.
Jass saab kaevata kolmel päeval nädalas ehk 2+2+2=6 meetrit nädalas. Et veebruaris on täpselt 4 nädalat, siis ta saab kuuga kaevata 6*4=24 meetrit. Isegi kui oleks veel üks esmaspäev 29. veebruaril, siis saaks ta kaevata 24+2=26 meetrit, ning kummalgi juhul ta välja ei pääse.
Jonn saab kaevata kahel päeval nädalas, kokku 4+4=8 meetrit, ja nelja nädala jooksul 8*4=32 meetrit. Seega saab tema edukalt põgeneda.
Informaatikas saab andmeid ja informatsiooni esitada paljudel viisidel (näiteks skeem vahemaade kohta, tekst ja joonis aja kohta). Vaja on aru saada ja osata mõelda erinevatel viisidel: "teisendada" informatsiooni. Selle ülesande lahendamiseks peame korraga mõtlema, arvutama ja kiiresti arutlema 3 minuti jooksul.
Selles ülesandes võib vangide vajaminevate kaevamistööde esitamiseks kasutada lihtsaid graafikuid ning nädala kaevamistööde esitamiseks histogrammi ja tabelit.
Ülesande lahendamise võti on panna see informatsioon kokku ja leida, kui palju tööd kumbki vang nädala jooksul teha suudab. Seejärel arvestada, et 1. veebruar on esmaspäev ning et veebruaris võib olla 28 või 29 päeva. Märgime, et andmepõhiste arvutuste puhul on informaatikas vaja pöörata erilist tähelepanu andmete muutumisulatusele.
Copyright © 2020 Bebras – International Challenge on Informatics and Computational Thinking.
Licensed under Creative Commons Attribution-ShareAlike 4.0 International License.
Flag icons by GoSquared.