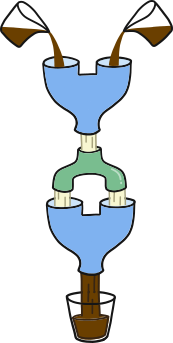
Kobras Kobil on mõistatuslik sinist värvi masin, mis on kujutatud joonisel 1. Masinal on kaks lehtrit.
Kui kobras valab mõlemasse lehtrisse šokolaadipiima, siis välja tuleb valge piim.
Kui kobras valab emba-kumba või ka mõlemasse lehtrisse valget piima, siis tuleb välja šokolaadipiim.
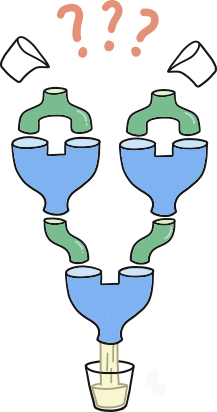
Kui kobras ühendab kaks masinat nii nagu joonisel 2 ja valab mõlemasse lehtrisse šokolaadipiima, siis tuleb välja šokolaadipiim. (Märkus: keskmine roheline ühenduslüli piima liigile mõju ei avalda.)
 |
 |
 |
| Joonis 1 | Joonis 2 | Joonis 3 |
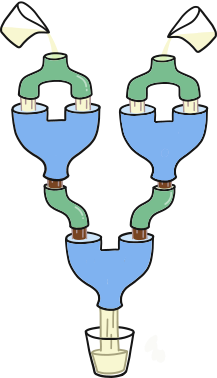
Mis liiki piima tuleb lehtritesse valada, et välja tuleks valge piim, kui ühendada kolm masinat nii, nagu näidatud joonisel 3?
[Raadionupud]
A. vasakusse valge piim, paremasse valge piim
B. vasakusse valge piim, paremasse šokolaadipiim
C. vasakusse šokolaadipiim, paremasse valge piim
D. vasakusse šokolaadipiim, paremasse šokolaadipiim
Õige vastus on A.
Nagu näeme jooniselt 4, tuleb valge piima saamiseks valada alumise masina mõlemasse lehtrisse šokolaadipiima.
 |
| Joonis 4 |
Et kahest ülemisest masinast tuleks šokolaadipiim, tuleb kummaski masinas vähemalt ühte lehtrisse valada valget piima. Ent ülemistes masinates on mõlema lehtri sisud samad, seega peab lõpus valge piima saamiseks valama mõlemasse ülemisse masinasse valget piima.
Elektroonikalülitust, mis võtab sisendiks ühe või mitu loogikaväärtust, sooritab loogilisi tehteid ja annab tulemuseks loogikaväärtuse, nimetatakse loogikalüliks. Näiteks AND, OR, NOT ja XOR on loogikalülid. Üks loogikalülidest on ka NAND, mille definitsioon on järgmine:
Huvitav on siin asjaolu, et kõik loogikaoperatsioonid saab avaldada ainult ühte tüüpi, NAND-lüli kaudu:
Selles ülesandes tähistab 0 valget piima ja 1 šokolaadipiima ning piimamasin sooritab tehte NAND. Joonisel 2 on kujutatud tehte AND esitamine ainult tehte NAND kaudu ning joonisel 3 on kujutatud tehte OR esitamine ainult tehte NAND kaudu.
Järves asuv küla koosneb 6 elumajast, millest igaühes elab üks või mitu kobrast. Lisaks on külas postkontor, kus keegi ei ela.
Kobrastel on kombeks kirja saatmisel kirjutada ümbrikule ainult saaja nimi, aga mitte tema aadressi. Aggelos on uus postiljon, kes ei tea, kes millises majas elab. Ta võtab tühja märkmiku ja hakkab posti kätte toimetama järgmise strateegia järgi:
Iga uue kirja saatmisel kirjutab Aggelos oma märkmikusse saatja nime ja aadressi.
Seejärel, kui kirja saaja aadress on märkmikus kirjas, toimetab ta kirja kohale.
Kui saaja aadressi märkmikus ei ole, siis teeb ta kirjast koopiad ja toimetab need kõigisse elumajadesse, välja arvatud kirja saatja omasse.
Kirja õige saaja vastab alati kirjale samal päeval. Seejärel kirjutab Aggelos oma märkmikusse tema nime ja aadressi ning toimetab vastuse kohale.
Esimesel päeval saadab Ebe kirja Genkile ja Maidel saadab kirja Ebele. Teisel päeval saadab Sutemeel kirja Ninnile.
Mitu kirja Aggelos kokku oma kahe esimese tööpäeva jooksul kohale toimetab?
[Tekstikast, täisarv]
Õige vastus on 14 (kohaletoimetatud kirja).
Kõigepealt saadab Ebe kirja Genkile. Aggelos ei tea, kus Genk elab, seetõttu viib ta kirja koopiad kõigisse 5 teise elumajja (5 kirja). Genk vastab ja Aggelos viib vastuse kohale (+1 kiri). Siis saadab Maidel kirja Ebele. Aggelos teab, kus Ebe elab, seega viib ta kirja otse talle (+1 kiri). Ebe vastab samal päeval ja Aggelos toimetab selle Maidelile (+1 kiri). Kokku toimetab Aggelos esimesel päeval kohale 8 kirja.
Teisel päeval saadab Sutemeel kirja Ninnile. Aggelos ei tea, kus Ninni elab, seetõttu viib ta kirja koopia kõigissee 5 teise elumajja (+5 kirja). Ninni vastab (+1 kiri). Kokku toimetabki Aggelos kahe esimese päeva jooksul kohale 14 kirja.
Ülal kirjeldatud protseduur on meetod, mille abil võrgukommutaator täidab oma MAC-aadressitabelit.
Härra Kopro leiutas iseärase muusikariista. Sellel on heli tekitamiseks ainult kolm klahvi: punane klahv (P), sinine klahv (S) ja roheline klahv (R). Muusikariist suudab tekitada 5 erinevat nooti, 1, 2, 3, 4 ja 5.
Mängimise alustamiseks tuleb kõigepealt vajutada klahvi P ning selle mõjul kõlab esimese noodina noot 1.
Seejärel oleneb muusikariista noot eelmisest kõlanud noodist ja vajutatud klahvist. Sinise (S) ja rohelise (R) klahvi vajutamise mõju kujutab järgmine "noodimuutuse diagramm":
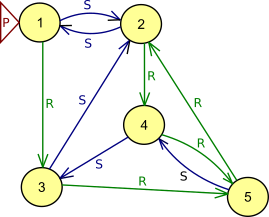
Iga kord, kui vajutatakse punast klahvi (P), kõlab taas noot 1.
Pala on nootide jada. Pala on reeglipärane, kui ta lõpeb kahe noodiga 1.
Näiteks klahvide jada P-R-S-S-P mõjul kõlavad muusikariistal noodid 1-3-2-1-1 (reeglipärane pala) ning klahvide jada P-R-S-P-S mõjul kõlavad noodid 1-3-2-1-2 (ebareeglipärane pala).
Milline järgmistest jadadest esitab reeglipärase pala?
[Raadionupud]
A. P-S-S-R-S-P
B. P-R-R-R-S-P
C. P-S-R-S-R-P
D. P-R-R-S-R-P
Õige vastus on B.
Vastuse võib leida muusikariista käitumise järgi, järgides diagrammi nooli.
Aga võib ka enne analüüsida: igas jadas vajutatakse klahvi P (punane) kaks korda, üks kord alguses ja teine kord lõpus. Diagrammil pole rohelist noolt, mis siseneks nooti 1. Seetõttu võime välistada vastusevariandid C ja D, sest need ei lõpe kahe noodiga 1.
Esimese jada (vastusevariant A) mõjul kõlab enne viimase P vajutamist noot 2. Seetõttu pole ka see reeglipärane jada.
Viimane järelejäänud võimalus on vastusevariant B, millega muusikariist mängib sellised noodid: 1-3-5-2-1-1.
Ülesandes kasutatud arvutusmudel kannab nime lõplik olekumasin (ehk lõplik automaat). Selliste mudelite abil saab arvutiteaduses lahendada paljusid ülesandeid, millest mõned on lihtsad ja mõned väga keerulised. Näiteks kasutatakse neid sageli programmeerimiskeelte kompilaatorite loomisel, need on programmid, mis loevad programmikoodi ja kontrollivad selle korrektsust.
Lõpliku olekumasina hea näide füüsilises maailmas on kohvimüügiautomaat. Enne kohvi valmistama hakkamist peab ta jõudma olekusse, kus me oleme sisestanud piisavalt raha. Seega mündi masinasse laskmisel võib olla masinale erinev mõju: kas loendada sisestatud rahasumma kogust ja oodata või näidata, et raha on sisestatud piisavalt, ja hakata kohvi valmistama. Sama tegevus, erinev mõju - olenevalt sellest, mis on varem toimunud, nagu ka ülesandes kirjeldatud muusikainstrumendi puhul.
Kobras Jaak töötab vee pudelitesse villimise tehases. Iga päev peab ta täitma olemasolevate pudelite hulgast võimalikult palju pudeleid 50-liitrises paagis oleva veega.
Täna on tal täitmiseks need 10 pudelit, kus silt pudeli peal näitab, mitu liitrit vett sinna mahub:
Milline on suurim arv pudeleid, mille kobras Jaak täielikult täita saab?
[Tekstikast, täisarv]
Õige vastus on 7 pudelit.
Kui meil on kaks tühja pudelit, kuhu mahub erinev kogus vett, siis suurema pudeli täitmisest me mingit eelist ei saa. Seetõttu võime ülesande lahendamiseks kõigepealt järjestada pudelid mahu järgi kõige väiksemast kõige suuremani:
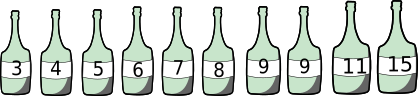
Nüüd võime täita pudelid veega, kuni vesi otsa saab. Seda tehes saame täielikult täita 7 pudelit, mis kasutavad ära 3+4+5+6+7+8+9=42 liitrit vett. Seejärel on meil järel 8 liitrit vett, aga iga ülejäänud pudel mahutab vähemalt 9 liitrit, seega rohkem pudeleid täita ei saa.
Ahneks algoritmiks (greedy algorithm) nimetatakse ükskõik millist algoritmi, mis järgib ülesande lahendamisel strateegiat, kus igal sammul tehakse lokaalselt optimaalne valik. Paljudes ülesannetes ei vii ahne strateegia optimaalse globaalse lahendini, aga võib anda mõistliku aja jooksul lokaalselt optimaalseid lahendeid, mis on globaalselt optimaalse lahendi lähendid.
Üldiselt on ahnel algoritmil viis komponenti:
Osa Kopramaast koosneb teatud arvust sildadega ühendatud saartest. Igal sillal on kogumassi piirang ning sõiduk, mille mass piirangut ületab, ei või sillast üle sõita.
All on kujutatud Kopramaa saarte kaart, kus saari esitavad ringid ja sildu lõigud. Iga silla juurde on kirjutatud tema kogumassi piirang.
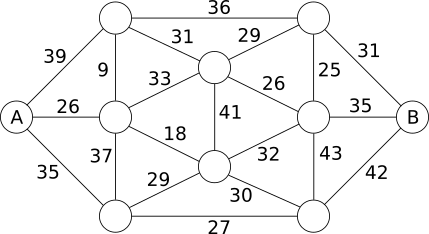
Ettevõttel "Kopramaa tarned" on vaja vedada saarelt A saarele B liiva. Milline on veoki suurim kogumass, et tal oleks veel võimalik sõita saarelt A saarele B?
[Raadionupud]
A. 42 tonni
B. 39 tonni
C. 32 tonni
D. 31 tonni
Õige vastus on C. 32 tonni ning tee on selline:
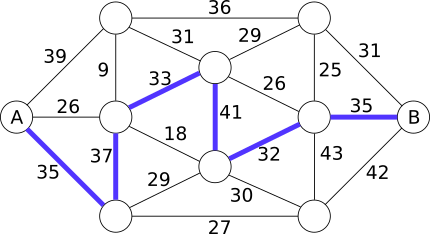
Üks viis vastuse leidmiseks on proovida raskema kaaluga, vaadata milliseid sildu saab kasutada ning seejärel vähendada kaalu, kuni läbitavaks muutub piisavalt sildu, mille kaudu pääseb saarele B.
Võime alustada kõige raskema kaaluga, mida üks sild välja kannatab: 43 tonni. Seda kannatab ainult üks sild, märgistame selle:
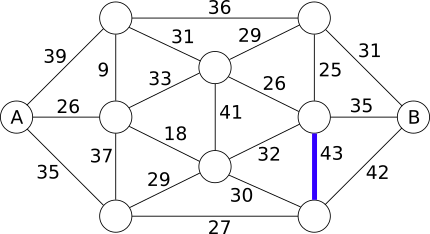
See ei moodusta teed saarelt A saarele B. Rohkemate sildade võimaldamiseks vähendame kaalu 42 tonnile ja lisame ühe silla:
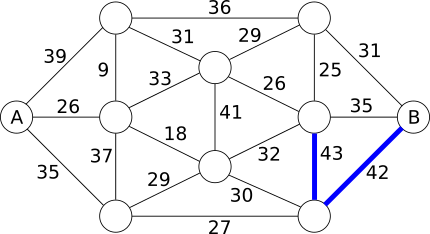
See ei moodusta teed saarelt A saarele B, seetõttu jätkame kaalu vähendamist, lisades sillad, mis kannatavad 41, siis 39, 37, 36 ja 35 tonni.
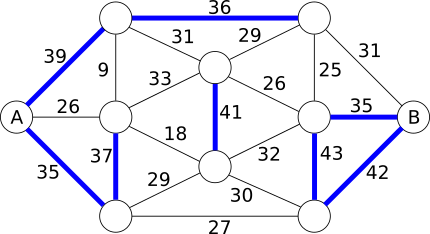
35 tonni juures oleme märgistanud juba 8 silda, aga tee saarelt A saarele B ikka puudub. Jätkame 33 tonniga, siis 32 tonniga, mis annab meile sellise võimalike silda hulga:
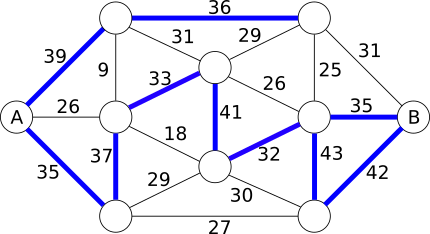
Nüüd on meil piisavalt sildu, et pääseda saarelt A saarele B. Nende sildade märgistused, mida me ei vaja, võime tühistada, et alles jääks ainult õige teekond:
Antud ülesanne on näide kõige laiema tee ülesandest graafiteoorias. Selle rakendused on näiteks võrgu maksimaalse ribalaiuse leidmine antud otspunktide vahel ja muud "pudelikaela" ülesanded. Seda võib vaadelda ka kui maksimaalse läbilaskevõime leidmise ülesande alamülesannet Fordi-Fulkersoni maksimaalse voo algoritmis.
Meie algoritm sarnaneb Kruskali algoritmiga, mida kasutatakse graafi vähima toesepuu leidmiseks.
Autotehas disainib uue laine autosid, mida hakatakse müüma tulevikus. Need autod erinevad üksteisest (a) värvi, (b) sisemuse, (c) rehvide ja (d) mootori poolest; igaühe puhul on 5 võimalust, mis on loetletud järgnevas tabelis.
| Värv | Sisemus | Rehvid | Mootor |
|---|---|---|---|
| 0. Sinine | 0. Must nahk | 0. Spordirehvid | 0. Diisel |
| 1. Punane | 1. Valge nahk | 1. Linnarehvid | 1. Bensiin |
| 2. Valge | 2. Must tekstiil | 2. Maanteerehvid | 2. Hübriid |
| 3. Must | 3. Valge tekstiil | 3. Pidamisrehvid | 3. Looduslik gaas |
| 4. Roheline | 4. Punane luks | 4. Luksusrehvid | 4. Elektri |
Tehas omistab kõigile võimalikele auto omaduste kombinatsioonidele numbrid 0 kuni 624.
Alustuseks omistatakse number 0 mudelile omaduste kombinatsiooniga 0 0 0 0, mis on sinine auto musta nahksisemuse, spordirehvide ja diiselmootoriga. Mudel 1 on auto omaduste kombinatsiooniga 0 0 0 1, mis on sinine auto musta nahksisemuse, spordirehvide ja bensiinimootoriga. Mudel 2 on auto omaduste kombinatsiooniga 0 0 0 2 ning mudel 5 on auto omaduste kombinatsiooniga 0 0 1 0.
Näiteks mudel omaduste kombinatsiooniga 2 0 1 4 on valge auto musta nahksisemuse, linnarehvide ja elektrimootoriga. Selle mudeli number on 259.
Mis mudelinumbriga on roheline auto punase lukssisemuse, luksusrehvide ja looduslikul gaasil töötava mootoriga?
[Tekstikast, täisarv]
Õige vastus on 623.
Loetletud omaduste numbrid on 4 (roheline), 4 (punane luks), 4 (luksusrehvid) ja 3 (looduslik gaas). Järjest kirjutades on see 4 4 4 3, mida võib lugeda kui viiendsüsteemi arvu, mis kümnendsüsteemi teisendades on 623. See ongi mudeli number... Aga kuidas me selle väärtuse saime?
Toodud näitest paneme tähele, et iga kord, kui suurendame viimase omaduse numbrit (mootori liik), liidame mudeli numbrile 1. Huvitavam on, et liikudes edasi rehvide spetsifikatsioonis, peame mudeli numbrile liitma mitte 1 (muidu läheks see segi mootori tüübi muutumisega), vaid 5. Miks 5? Sest mootori jaoks on ainult 5 võimalust ning pärast neid peab iga järgneva mudeli number muutuma kuskil mujal - siin rehvide võimaluste juures.
Samamoodi mõeldes leiame, et liikudes edasi mööda sisemuse variante, liidame mudeli numbrile 25. Miks 25? Sest kahe kõige parempoolsema omaduse jaoks on 5x5=25 võimalikku valikut. Analoogiliselt toob järgmise värvi valimine kaasa mudeli numbri muutumise 5x5x5=125 võrra.
Me saame seega lugeda, mitu korda iga omadust on "uuendatud" baasomaduse suhtes, ja liita kõik kokku, korrutades neid eelpool selgitatud teguritega:
(värv) 4 x 125 + (sisemus) 4 x 25 + (rehvid) 4 x 5 + (mootor) 3 = 623.
Teine võimalus on panna tähele, et uuritava mudeli kõik omadused peale mootori on suurima võimaliku tähisega, ainult mootor on suuruselt teise tähisega. Seega peaks mudeli tähis olema ühe võrra väiksem maksimaalsest võimalikust:
624 - 1 = 623.
Arvusüsteemi baasi muutmine on väga kasulik, sest nii saame edasi saata informatsiooni, mis kümnendsüsteemis poleks nii lihtne.
Kümnendsüsteem, mida me igapäevaelus kasutame, ei ole see viis, kuidas arvutid arve mälus hoiavad. Arvutites on kasutusel kahendsüsteem: arvud koosnevad ainult numbritest 0 ja 1. Kui sisestad arvutisse arvu, siis teisendab arvuti selle kahendsüsteemi ja teeb oma arvutused sellega.
Tegelikult hoiavad arvutid kahendsüsteemis üldse kõiki andmeid: mitte ainult arve, vaid ka näiteks heli, pilte, filme, 3D-mudeleid jne.
Kobras Ann saadab salakoodide abil sõpradele sõnumeid. Praegu korraldab ta salajast pidu ja soovib saata oma sõpradele sissepääsuks vajaliku parooli 3124.
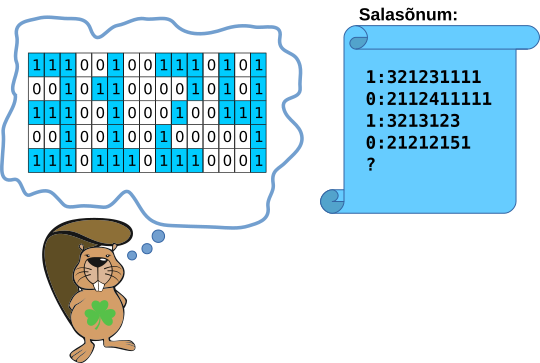
Mis on selle salasõnumi viimane rida?
[Raadionupud]
A. 0:3131331
B. 1:321231111
C. 1:3131331
D. 1:231231111
Õige vastus on C.
Sõnumi iga rea esimene number ütleb, kas vastav rida joonisel algab valge või sinise ruuduga (0 tähendab valget ja 1 sinist). Kooloni järel tulevad numbrid näitavad, mitu ühte värvi ruutu kummastki vahelduvast värvist järgneb.
Joonise viimane rida algab sinise ruuduga (1). Koolonile järgneb arv, mis näitab seda värvi ruutude arvu (3 sinist ruutu). Sellele järgneb 1 valge ruut, siis 3 sinist ruut, siis 1 valge ruut jne:
| esimene ruut sinine | : | 3s | 1v | 3s | 1v | 3s | 3v | 1s |
|---|---|---|---|---|---|---|---|---|
| 1 | : | 3 | 1 | 3 | 1 | 3 | 3 | 1 |
Vastusevariant A ei saa olla õige, sest alguse 0: tähendab, et esimene ruut peaks olema valge nagu joonise 2. ja 4. reas. Õieti kirjeldab see variant joonise rida, mis on täpselt vastupidine sellele, mida Ann soovib.
Vastusevariant B ei saa olla õige, sest see kirjeldab joonise rida, mis on identne joonise esimese reaga: pärast 3 sinist ruutu on 2 valget ruutu jne.
Vastusevariant D ei saa olla õige, sest joonise viimane rida peaks siis algama 2 sinise ruuduga.
Ülesanne toob sisse järjest mitu andmete kodeerimisega seotud mõistet:
Andmete töötlemise puhul on tavaline, et meil on sama informatsiooni esitamiseks mitu viisi ja vaja on teisendada andmeid ühest esitusest teise.
Selles ülesandes sisse toodud sarikodeerimine (run-length encoding, RLE) on kadudeta pakkimise väga lihtne vorm. Sarikodeerimise algoritmi rakendatakse jadadele, kus samu väärtusi esineb tihti mitu korda järjest. Selline jada kodeeritakse nii, et iga väärtus salvestatakse ainult üks kord, ning selle järele kirjutatakse selle esinemiskordade arv. Enamikel juhtudel tuleb väljundi suurus niimoodi sisendi suurusest väiksem, aga halvimal juhul võib see olla ka suurem.
Selles ülesandes on väärtuste salvestamisest loobutud, eeldades, et iga järgnev kordade arv vastab väärtusele, mis on eelmise väärtuse vastand. (Kas suudad leida näitejoonise, kus Ann sellise lähenemise tõttu raskustesse satub? Kas sellised joonised võivad esineda paroolide esitustena?)
Ülesande lahendamiseks on vaja üldistamise ja algoritmilise mõtlemise oskust. Esmalt peab tuletama sarikodeerimise algoritmi, võrreldes vastavaid ridu tabelis ja salasõnumis. Seejärel peab rakendama seda algoritmi joonise viimasele reale ja saama kätte sõnumi viimase rea.
Lõpuks tasub märkida, et RLE ei ole tugev krüptimisalgoritm. Mõne salajase sõnumi nägemise järel pole väga raske algoritmi ära arvata, isegi ilma vastavaid paroole teadmata. Seetõttu ei tasuks seda kasutada tõeliselt tähtsate saladuste krüptimiseks.
Luku avamiseks tuleb pöörata lukul neli numbrit õigesse asendisse. Iga numbrit saab pöörata sammukaupa edasi või tagasi.
Joonisel on lukul valitud numbrikombinatsioon 2719. Numbrit 7 võime ühe sammuga pöörata edasi numbriks 8 või tagasi numbriks 6. Kui numbrit 9 pöörata edasi, siis muutub ta numbriks 0. Samamoodi, kui numbrit 0 pöörata tagasi, siis saab temast number 9.
Milline on vähim sammude koguarv, mida on luku avamiseks vaja, kui praegused numbrid on 2719 ning luku avab kood 4383?
[Raadionupud]
A. 21
B. 19
C. 17
D. 13
E. 12
Õige vastus on D. 13.
Iga numbri puhul saame liikuda edasi või tagasi. Nendest pööramistest valime väiksema.
Valides iga numbri puhul väiksema pööramiste arvu, saame: esimese numbri puhul kaks sammu edasi (2→3→4), teise numbri puhul neli sammu tagasi (7→6→5→4→3), kolmanda numbri puhul kolm sammu tagasi (1→0→9→8) ja viimase numbri puhul neli sammu edasi (9→0→1→2→3). See annab meile ühtekokku 13 sammu.
Valed vastusevariandid
A. 21 (=2+6+7+6) saame sammude arvuks näiteks siis, kui pöörame esimest numbrit edasi (2→3→4), teist numbrit edasi (7→8→9→0→1→2→3), kolmandat numbrit edasi (1→2→3→4→5→6→7→8) ja viimast numbrit tagasi (9→8→7→6→5→4→3).
B. 19 (=2+6+7+4) saame sammude arvuks näiteks siis, kui pöörame iga numbrit edasi, st (2→3→4), (7→8→9→0→1→2→3), (1→2→3→4→5→6→7→8) ja (9→0→1→2→3).
C. 17 (=2+4+7+4) saame sammude arvuks näiteks siis, kui pöörame esimest numbrit edasi (2→3→4), teist numbrit tagasi (7→6→5→4→3), kolmandat numbrit edasi (1→2→3→4→5→6→7→8) ja neljandat numbrit edasi (9→0→1→2→3).
E. 12 on eksitav väärtus kui 13 sammu vale kokkulugemine ja 13-st väiksem arv.
See ülesanne on minimeerimisülesanne algoritmiselt määratud väärtuste hulgal. Minimeerimine on optimeerimisülesannete alamliik.
Selles ülesandes tuleb meil minimeerida sõltumatute väärtuste summa. Selle saavutamiseks minimeerime iga väärtust eraldi. Paneme tähele, et sõltumatute väärtuste summa miinimum on alati võrdne nende väärtuste miinimumide summaga.
Väärtused ise on algoritmiliselt määratud, sest iga numbrit võib pöörata edasi või tagasi. See tähendab, numbrist 9 numbri 2 saamiseks võime teha kolm sammu edasi (9→0→1→2) või seitse sammu tagasi (9→8→7→6→5→4→3→2). Paneme tähele, et edasisammude arvu ja tagasisammude arvu summa on 10, sest see on tsükli pikkus.
Seega võtame iga numbri puhul sammude arvust vähima ja nende vähimate arvude summa ongi kogusumma miinimum.
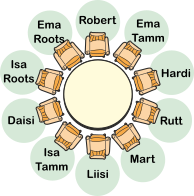
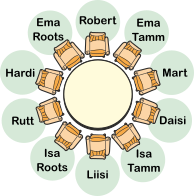
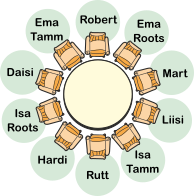
Mart korraldab kopraperedele õhtusöögi. Sinna kutsus ta oma sõbra Roberti ja veel kaks kopraperet: isa ja ema Tamme koos poja Hardi ja tütre Rutiga ning isa ja ema Rootsi koos tütarde Liisi ja Daisiga.
Vestluste alustamise soodustamiseks pani Mart paika mõned reeglid, kuidas osalejad ümmarguse õhtusöögilaua ümber paigutada.
Kaks naissoost kobrast ei istu kõrvuti.
Sama perekonna isa ja ema ei istu kõrvuti.
Noored koprad ei istu oma vanemate kõrval.
Milline järgmistest on Mardi reeglitele vastav kohtade paigutus?
[Raadionupud]
| A | B | C | D |
|---|---|---|---|
 |
 |
 |
 |
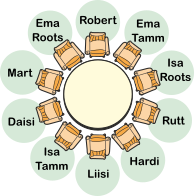
Õige vastus on B.
Vastusevariandis A istuvad ema ja isa Roots kõrvuti, mis on vastuolus 2. reegliga. Lisaks istub Daisi oma isa kõrval, mis on vastuolus 3. reegliga.
Vastusevariandis C istub Liisi oma isa kõrval, mis on vastuolus 3. reegliga.
Vastusevariandis D istub Daisi ema Tamme kõrval, mis on vastuolus 1. reegliga. Rutt istub oma isa kõrval ja Daisi istub oma isa kõrval, mis on vastuolus 2. reegliga.
Vastusevariandis B on kõik reeglid (tingimused) täidetud, seetõttu see on õige vastus.
Õhtusöögilaua ülesanne on tegelikult üldisema "kitsenduste" ülesande lihtsam variant. Meil on antud hulk kitsendusi (reegleid või piiranguid) ja väärtuste piirkond ning me peame leidma lahendi, mis rahuldab kõiki kitsendusi.
Selle saavutamiseks loome andmetest mudeli ja seejärel ehitame lahendi järk-järgult üles. Määrame muutujad, nende võimalikud väärtused, kehtivad kitsendused. Selles ülesandes on muutujateks kobraste hõivatud istekohad.
Seejärel püüame leida lahendi samm-sammult, omistades muutujatele ühekaupa sobivad väärtused ning kanname väärtuste omistamise mõju edasi ülejäänud muutujatele. Mõnikord võib juhtuda, et väärtuste omistamisel tekib tõrge, sel juhul võtame samme tagasi, omistame muutujatele teised väärtused ja proovime uuesti.
Selles ülesandes on meie töö lihtsam: väärtused on antud valikvastuste kujul ning meil on vaja lihtsalt kontrollida, kas nad rahuldavad kitsendusi.
Järgmisi reegleid järgides saab moodustada kauneid mustreid:
reegel: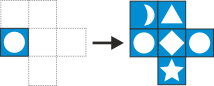 
reegel: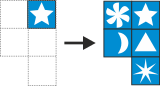 
reegel: 
Näiteks alustades kujundist 
, võime saada kujundi 
, kui rakendada kaks korda 3. reeglit.
Kui alustada ühestainsast ringist (
), siis millise järgmistest mustritest saab moodustada?
[Raadionupud]
A. 
B. 
C. 
D. 
Õige vastus on A.
Järgneval joonisel on näha, kuidas ühest ringist () alustades saab moodustada mustri A. Rakendame üksteise järel reegleid 1, 2 ja 3:
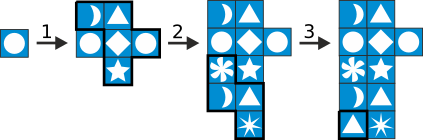
Seejärel rakendame parempoolsele (joonisel noolega näidatud) ringile 1. reeglit ning seejärel uuesti 2. reeglit ja 3. reeglit.
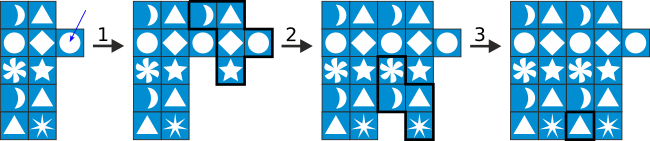
Siin me rakendasime reegleid järjekorras 1 2 3 1 2 3, aga sama tulemuse saamiseks on võimalikud ka muud järjekorrad.
Selleks, et näha, et muud mustrid ei ole võimalikud, on meil vaja kasutada "trikke". (Loomulikult võib proovida koostada mustreid B, C ja D uuesti ja uuesti katsetades ning mitte kunagi tulemusele jõudes, aga siis ei või olla 100% kindel, et mõnda võimalust ei unustatud või ei tehtud viga...).
Muster D ei ole võimalik: 1. reegel on ainuke reegel, mille abil saab moodustada ruudu (
). Seejuures tekib iga kord koos ruuduga juurde ka ring (
). Et alustame ühest ringist, siis sisaldab iga võimalik muster alati ühe võrra rohkem ringe kui ruute. Mustris D on ringe sama palju kui ruute, seepärast mustrit D nende reeglitega moodustada ei saa.
Muster B ei ole võimalik: 1. reegel on ainuke reegel, mis tekitab 5-harulise tähe (
). See 5-haruline täht pannakse alati ruudu () alla. Mustri B kõige parempoolsema tähe kohal ei ole ruutu, seetõttu ei saa ka mustrit B nende reeglitega moodustada.
Muster C ei ole võimalik: Eelmistega analoogiliselt, ainuke reegel, millega mustrisse lisandub 7-haruline täht (
) (2. reegel), paneb ühtlasi selle kohale kolmnurga (
). Muster C sisaldab 7-harulist tähte ilma selle kohal oleva kolmnurgata, seetõttu ei saa nende reeglitega moodustada ka mustrit C.
Teine (ja lühem) argument: kõigist reeglitest laiendab ainult 1. reegel mustrit paremale. Seetõttu peab iga mustri kõige parempoolsemas veerus esinema ring (). Mustrites B, C ja D pole see aga nii.
Et arvuti saaks oma ülesandeid sooritada, peab keegi (sageli programmeerija) ütlema arvutile ühel või või teisel viisil, mida täpselt teha tuleb. Sageli öeldakse seda arvutile programmi kirjutamise teel, aga mõnikord võib programmeerija lihtsalt defineerida reeglite hulga, mida arvuti järgima peab, nagu tegime selles ülesandes. Praktikas pannakse reeglid tavaliselt kirja tekstina ja neid ei selgitata piltide abil. Aga kes teab, ehk tulevikus, kui arvutid targemaks muutuvad, võib piisata ka sellest, et joonistada vajalikud tegevused üles piltidena...
Informaatika ei tegele ainult sellega, kuidas arvuti jaoks reegleid kirja panna. Mõned teadlased uurivad ka, mis liiki reegleid on parem kasutada ja mis on teatavate reeglite järgimisel võimalik või võimatu. Sageli kasutavad nad samasuguseid trikke, mille abil meie põhjendasime, miks antud reeglite abil pole võimalik koostada mustreid B, C ja D. Ning tõesti, sageli rakendatakse nendes trikkides loendamist või matemaatikat. (Seda osa informaatikast nimetatakse teoreetiliseks informaatikaks.)
Bruno oli koolivaheajal kaks nädalat emal abiks nende kodukohvikus.
Mõlema esmaspäeva hommikul sai ta ema käest 40€ väärtuses münte ja pani need kohviku kassasse vahetusrahaks.
Iga tööpäeva õhtul märkis ta üles kassas oleva raha kogusumma ja sai sellise graafiku:
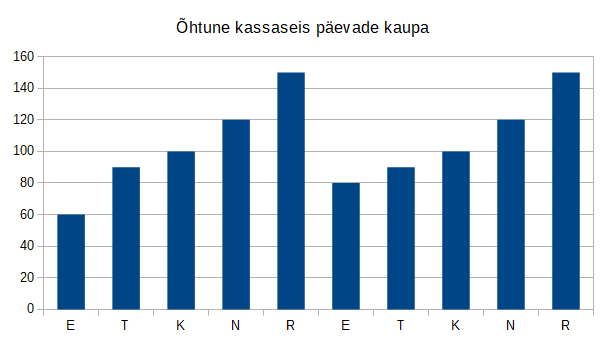
Mõlema reede õhtul võttis ta kassast kogu raha välja ja andis emale.
Mitu eurot oli kohviku suurim päevane sissetulek?
[Tekstikast, täisarv]
Õige vastus on 40€.
Kohviku käibest parema ülevaate saamiseks toome graafikul välja eraldi kassajäägi hommikul ja õhtul (seejuures on oluline mitte unustada esmaspäeva hommikul algseisuks sisse pandud 40€):
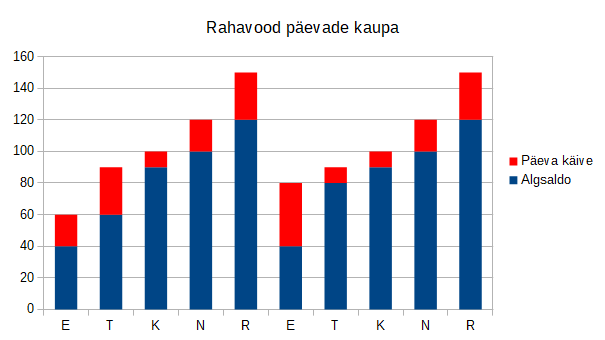
Veel selgem on asi, kui jätame graafikult välja hommikuse jäägi ja keskendume päeval lisandunud summale:
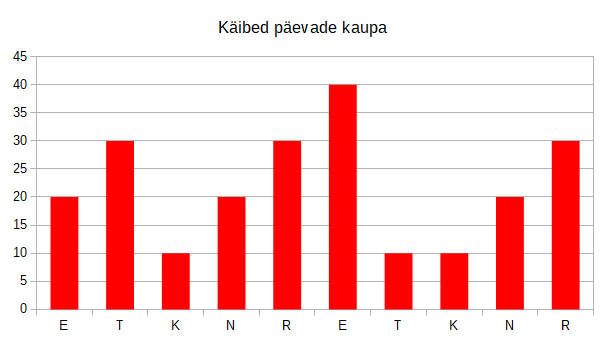
Nüüd on ilmne, et kõige suurema summa, 40€, teenis kohvik teise nädala esmaspäeval.
See ülesanne illustreerib, kuidas andmete esitusviis võib nende põhjal mõnele küsimusele vastamise teha kas lihtsamaks või keerulisemaks. Kui graafiku aluseks olevad andmed on arvutustabelis või andmebaasis, saab esituse parandamiseks vajaliku teisenduse lasta ära teha arvutil. Mida rohkem on andmeid, seda suurem on sellisest automaatsest parandamisest saadav kasu.
Sõnade otsimiseks tekstist võib kasutada regulaaravaldisi (regular expressions). Need võivad sisaldada metamärke, mis määravad keerukamaid otsingureegleid.
Mõned metamärkide näited:
[:space:] – tühikud, näiteks b[:space:]e leiab teksti b e,
? – erisümbol, mis määrab, et selle ees olev märk võib tekstis esineda või puududa, näiteks be?b leiab nii beb kui ka bb.
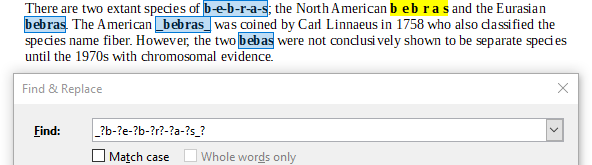
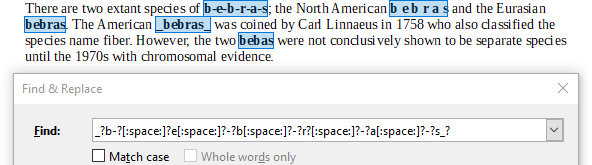
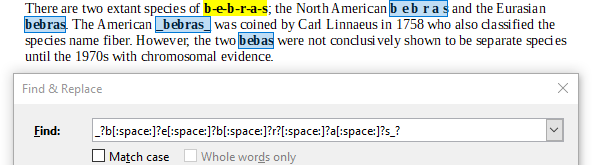
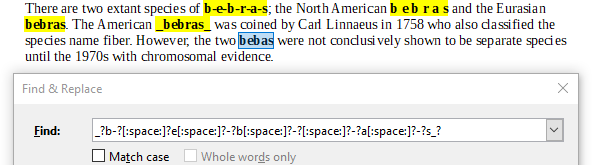
Järgnevas tekstis esineb sõna "bebras" viis korda (paksus kirjas esile toodud), iga kord erinevalt kirjutatuna:
There are two extant species of b-e-b-r-a-s; the North American b e b r a s and the Eurasian bebras. The American bebras was coined by Carl Linnaeus in 1758 who also classified the species name fiber. However, the two bebas were not conclusively shown to be separate species until the 1970s with chromosomal evidence.
Millise regulaaravaldise peaks otsinguaknasse sisestama, et leida tekstist sõna "bebras" kõik viis varianti?
[Raadionupud]
A. _?b-?e-?b-?r?-?a-?s_?
B. _?b-?[:space:]?e[:space:]?-?b[:space:]?-?r?[:space:]?-?a[:space:]?-?s_?
C. _?b[:space:]?e[:space:]?b[:space:]?r?[:space:]?a[:space:]?s_?
D. _?b-?[:space:]?e[:space:]?-?b[:space:]?-?[:space:]?-?a[:space:]?-?s_?
Õige vastus on B. _?b-?[:space:]?e[:space:]?-?b[:space:]?-?r?[:space:]?-?a[:space:]?-?s_?.
Vaatleme iga avaldist eraldi.
Avaldis A ei leia varianti "b e b r a s", kus tähtede vahel on tühikud:
Avaldis B leiab kõik viis varianti:
Avaldis C ei leia varianti, kus tähtede vahel on sidekriipsud:
Avaldis D leiab vaid selle variandi, kus täht "r" puudub:
Regulaaravaldisi kasutatakse programmeerimises väga sageli, näiteks osaliselt kokku langevate tekstide, märgihulkade, sõnade otsimisel, tekstiridade valideerimisel, samuti sümbolite või sõnade asendamiel. Neid saab kasutada ka andmete valideermisel, näiteks kui paroolile seatakse minimaalse tähemärkide arvu või suur- ja väiketähtede, numbrite või erimärkide olemasolu nõuded.
Kobras Tom tahtis jäädvustada ühele pildile kõik oma sõbrad metsas. Selle saavutamiseks otsustas ta luua panoraampildi, kombineerides mitu väiksemat pilti. Hiljem pannakse need pildid kokku ja luuakse üks panoraampilt. Siin on kõik tema tehtud pildid:
Mitut kobrast on lõpuks panoraampildil?
[Tekstikast, täisarv]
Õige vastus on 7.
Need väiksemad pildid on moodustatud ühest suurest pildist. Nagu näeme alltoodud panoraampildilt, on sellel 7 kobrast.
Loodetavasti olete juba uurinud oma kaamera ja mobiiltelefoni erivõimalusi, sealhulgas panoraamvaadet. See võimaldab ühendada mitu pilti üheks suuremaks pildiks. Seetõttu on see ka informaatika.
Kopravanaema sünnipäeva puhul kogunesid tema juurde kõik tema 5 lapselast. Kingituseks tõid nad lauamängu 4 inimesele ja lubasid külastada vanaema pühapäeviti sagedamini, alates tänasest pühapäevast:
Milline kolmest kopralapsest koosnev rühm kohtub vanaema sünnipäeva järel uuesti esimesena, et temaga lauamängu mängida?
[Raadionupud]
A. Albert, Britta, Cassie
B. Cassie, Deniss, Elsbet
C. Britta, Cassie, Elsbet
D. Albert, Cassie, Deniss
Õige vastus on C (Britta, Cassie, Elsbet), kes kohtuvad 24 nädala pärast.
Kaks kobrast X ja Y, kes tulevad tagasi fX ja fY nädala pärast, kohtuvad omavahel uuesti VÜK(fX, fY) nädala pärast, kus VÜK tähistab vähimat ühiskordset.
Seda võib laiendada kolme kopra juhule: VÜK(fX, fY, fZ) = VÜK(VÜK(fX, fY), fZ).
Ülesannet saab lahendada vähima ühiskordse leidmisega. Vähima ühiskordse ja suurima ühisteguri leidmise algoritmide abil saab lahendada väga erinevaid ülesandeid koostisosade kokkusobitamisest planeetide vastasseisude ja krüptograafiani.
Kõvaketas on salvestusruumi haldamiseks jagatud kindla suurusega klastriteks. Faili salvestamisel võtab see alati enda alla täisarvu klastreid. Kui faili suurus ei jagu klastri suurusega, jääb viimase hõivatud klastri lõpust osa ruumi lihtsalt kasutamata.
Järgneval joonisel on kujutatud 16 KB suurusteks klastriteks jaotatud kõvaketta kasutus, kus juba hõivatud klastrid on hallid ja veel vabad klastrid valged.
Kettale kirjutatakse ükshaavad järgmised failid: kõigepealt fail A suurusega 20 KB, siis fail B suurusega 18 KB, siis fail C suurusega 34 KB ning lõpuks fail D suurusega 48 KB. Operatsioonisüsteem püüab leida failide salvestamiseks järjestikused vabad klastrid, et vältida failide fragmenteerumist, st faili tükeldamist erinevate kettaosade vahel, mis vähendab arvuti jõudlust.
Üks lähenemine failide fragmenteerumist vähendada on selline.
Otsida esimene järjestikuste vabade klastrite kogum, kuhu mahub terve fail.
Kui sellist kogumit pole, siis tükeldada fail nii, et saadavad tükid saab paigutada esimestesse vabadesse klastritesse.
Milline näeb failisüsteem välja pärast seda, kui eelkirjeldatud reeglite järgi kirjutatakse sinna failid A (punane), B (roheline), C (sinine) ja D (kollane)?
[Raadionupud]
A. 
B.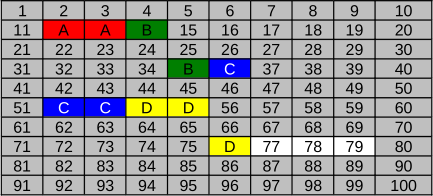 
C.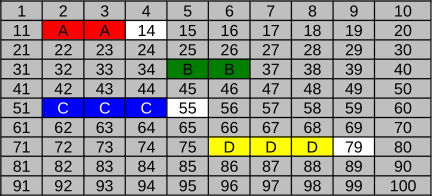 
D.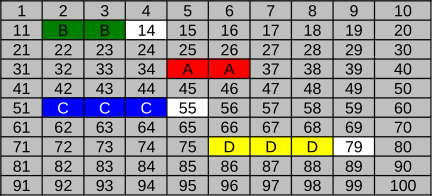 
Õige vastus on C.
Fail A (20 KB) kirjutatakse klastritesse 12 ja 13 (vaba ruumi 32 KB jaoks).
Fail B (18 KB) kirjutatakse klastritesse 35 ja 36 (vaba ruumi 32 KB jaoks). Klaster 14 jääb kasutamata, sest selle kasutamine põhjustaks faili B fragmenteerimise, mida saab vältida klastrite 35 ja 36 kasutamisega.
Fail C (34 KB) kirjutatakse klastritesse 52, 53 ja 54 (vaba ruumi 48 KB jaoks).
Fail D (48 KB) kirjutatakse klastritesse 76, 77 ja 78 (vaba ruumi 48 KB jaoks).
Variant A ei ole õige vastus, sest selle kohaselt hõivab fail B ainult ühe klastri. Kuna klastri suurus on 16 KB, et saa 18 KB suurune fail ühte klastrisse mahtuda. Samamoodi ei saa ka fail C mahtuda kahte klastrisse.
Variant B ei ole õige vastus, sest selle kohaselt fail B salvestamisel fragmenteeriti, aga 1. reegli kohaselt seda ei tehta, kui leidub piisava suurusega järjestikuste vabade klastrite hulk. Samamoodi fragmenteeriti asjatult ka failid C ja D.
Variant D ei ole õige vastus, sest selle kohaselt salvestati fail A klastritesse 35 ja 36, kuigi faili A salvestamise ajal olid vabad ka klastrid 12 ja 13 ning reegli 1 kohaselt oleks pidanud faili A salvestama esimesse piisava suurusega vabasse alasse.
See ülesanne näitab, kuidas kõvakettal informatsiooni hoitakse ja selgitab failide fragmenteerumise mõistet.
Ülesande näites kannatab failisüsteemi algseis juba välise fragmenteerumise all, mille tagajärjel on vabade järjestikuste klastrite kogumid kettal väikesed. Väline fragmenteerumine tekib, kui luuakse, muudetakse või kustutatakse erinevate suurustega faile.
Kui luuakse suur fail ja kettal pole selle salvestamiseks piisavalt suurt järjestikuste vabade klastrite kogumit, siis tükeldatakse fail väiksemateks osadeks ja kirjutatakse need failisüsteemi. Seda protsessi nimetatakse faili fragmenteerimiseks. Selle puuduseks on kõvaketta jõudluse vähenemine.
Kolmas fragmenteerumise liik esineb arvuti operatiivmälu (RAM) halduses. Ka operatiivmälu on jaotatud kindla suurusega lehekülgedeks ja selle jagamine programmide vahel toimub lehekülgede kaupa. Tavaliselt kasutab programm mitut lehekülge, kusjuures tihti ei saa viimane lehekülg täielikult täidetud ning mälusse jääb vaba ruum, mida teised programmid enam kasutada ei saa. Seda nimetatakse sisemiseks fragmenteerumiseks.
Copyright © 2020 Bebras – International Challenge on Informatics and Computational Thinking.
Licensed under Creative Commons Attribution-ShareAlike 4.0 International License.
Flag icons by GoSquared.