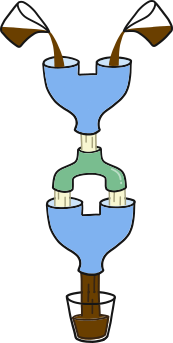
У бобра Димы имеется магическая машина синего цвета, которая изображена на рисунке 1. У машины имеется две воронки.
Если бобр наливает в обе воронки шоколадное молоко, то на выходе получает белое молоко.
Если бобр наливает в ту или иную воронку, или в обе воронки белое молоко, то на выходе он получает шоколадное молоко.
Если бобр объединяет две машины таким образом, как изображено на рисунке 2, и в обе воронки наливает шоколадное молоко, то на выходе он получает шоколадное молоко. (Внимание: расположенный в середине зелёный переходник не влияет на вид молока.)
 |
 |
 |
| Рисунок 1 | Рисунок 2 | Рисунок 3 |
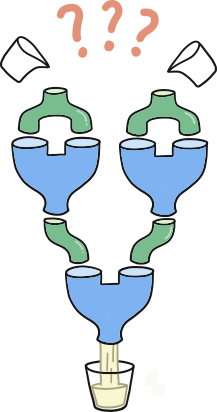
Какой вид молока надо налить в каждую воронку для получения на выходе белого молока, если объединить три машины, как показано на рисунке 3?
[Raadionupud]
A. в левую белое молоко, в правую белое молоко
B. в левую белое молоко, в правую шоколадное молоко
C. в левую шоколадное молоко, в правую белое молоко
D. в левую шоколадное молоко, в правую шоколадное молоко
Правильный ответ A.
Как видно на рисунке 4 для получения белого молока необходимо в обе воронки нижней машины налить шоколадное молоко.
 |
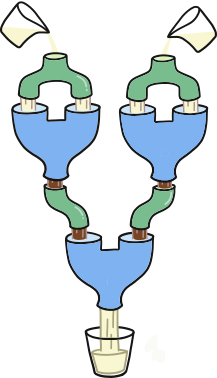| Рисунок 4 |
Для того чтобы из двух верхних машин на выходе получить шоколадное молоко, по меньшей мере в одну из воронок каждой из этих машин следует налить белое молоко. Так как в верхних машинах содержимое обеих воронок одинаково, то для получения в итоге белого молока необходимо налить в обе верхних машины белое молоко.
Элемент электроники, который на входе имеет одно или несколько логических значений, выполняет логические операции и даёт в результате логическое значение, называется логическим вентилем. Например, AND, OR, NOT и XOR являются логическими вентилями. Одним из логических вентилей является также NAND, который можно задать следующим образом:
Интересен здесь тот факт, что все логические операции можно выразить только через один тип вентилей - NAND вентиль:
В данном задании 0 обозначает белое молоко и 1 - шоколадное молоко, а машина выполняет NAND действия. На рисунке 2 операция AND представлена только с помощью операции NAND, а на рисунке 3 операция OR представлена только с помощью операции NAND.
Расположенная на озере деревня состоит из 6 домов, и бобры живут в них вместе или раздельно. К тому же в деревне есть почтовая контора, в которой никто не живёт.
У бобров есть традиция при отправке письма написать на конверте только имя получателя, но не его адрес. Анджи - это новый почтальон, который пока не знает кто в каком доме живёт. Он берёт чистый блокнот и доставку почты он организует по следующей стратегии:
При отправке каждого нового письма Анджи записывает в блокнот имя отправителя и его адрес.
Далее, если адрес получателя письма уже имеется в блокноте, Анджи доставляет письмо по адресу.
Если имени получателя нет в блокноте, то он делает копии с письма и доставляет их во все жилые дома за исключением того, откуда было отправлено письмо.
Правильный получатель письма всегда отвечает на него в тот же день. Затем Анджи записывает в свой блокнот его имя и адрес и доставляет ответ.
В первый день Елена отправила письмо Гене, а Миша отправил письмо Елене. На другой день Сергей отправил письмо Нине.
Сколько писем всего доставит Анджи за свои первые два рабочих дня?
[Tekstikast, täisarv]
Правильный ответ 14 (доставленных по адресу писем).
Прежде всего Елена отправляет письмо Гене. Анджи не знает, где живёт Гена, поэтому он доставляет копии письма во все оставшиеся 5 домов (5 писем). Гена отвечает, и Анджи доставляет ответ по адресу (+1 письмо). Далее Миша отправляет письмо Елене. Анджи уже знает, где живёт Елена, и поэтому он доставляет письмо лично ей (+1 письмо). В тот же день Елена отвечает, и Анджи доставляет письмо Мише (+1 письмо). Итого, в первый день Анджи доставит 8 писем.
Во второй день Сергей отправляет письмо Нине. Анджи не знает, где живёт Нина, поэтому он доставляет копии письма во все оставшиеся 5 домов (+5 писем). Нина отвечает (+1 письмо). Таким образом, за свои первые два рабочих дня Анджи доставит 14 писем.
Вышеописанная процедура является методом, с помощью которого сетевой коммутатор заполняет свою таблицу с MAC адресами.
Господин Карро изобрёл особенный музыкальный инструмент. Для получения звука используются три клавиши: красная клавиша (К), синяя клавиша (С) и зелёная клавиша (З). Музыкальный инструмент может издавать 5 различных нот - 1, 2, 3, 4 и 5.
Прежде всего в начале игры необходимо нажать клавишу К - тогда первая нота будет звучать как нота 1.
Далее звучание ноты музыкального инструмента зависит от предыдущей прозвучавшей ноты и нажатой клавиши. Влияние нажатия синей (С) и зелёной (З) клавиш можно увидеть на следующей "диаграмме преобразования нот":
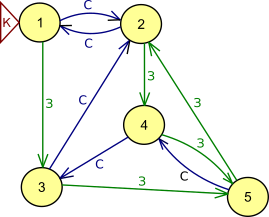
Каждый раз, когда нажимают красную клавишу (К), вновь звучит нота 1.
Произведение - это последовательность нот. Произведение считается правильным, если оно оканчивается двумя нотами 1.
Например, при нажатии на клавиши в последовательности К-З-С-С-К звучат ноты 1-3-2-1-1 (правильное произведение), а при нажатии на клавиши в последовательности К-З-С-К-С звучат ноты 1-3-2-1-2 (неправильное произведение).
Какая из приведённых последовательностей представляет собой правильное произведение?
[Raadionupud]
A. К-С-С-З-С-К
B. К-З-З-З-С-К
C. К-С-З-С-З-К
D. К-З-З-С-З-К
Правильный ответ B.
Ответ можно получить, основываясь на поведении музыкального инструмента и отслеживая стрелки на диаграмме.
Однако можно сначала проанализировать ситуацию: в каждой последовательности клавиша К (красная) нажимается два раза - один раз в начале и второй раз в конце. На диаграмме нет зелёной стрелки, которая бы входила в ноту 1. Таким образом, мы можем исключить варианты C и D, потому что они не оканчиваются двумя нотами 1.
В результате первой последовательности (вариант ответа A) перед последним К нажатием звучит нота 2. Это не позволяет нам считать произведение правильным.
Последним оставшимся вариантом ответа является B. В этой последовательности музыкальный инструмент издаёт следующие ноты: 1-3-5-2-1-1.
Использованная в задании вычислительная модель носит название машины с конечным числом состояний (или конечный автомат). С помощью этой модели в компьютерных науках можно решить множество заданий, некоторые из которых простые, а некоторые сложные. Например, их часто используют при создании компиляторов языков программирования. Это программы, которые считывают программный код и проверяют его на корректность.
В физическом мире отличным примером машины с конечным числом состояний является автомат по продаже кофе. Прежде чем начать варить кофе, он должен оказаться в таком состоянии, когда мы бросили в него достаточное количество денег. Таким образом, закидывание денег в машину может оказывать на машину различное влияние: пересчитать количество внесённый денег и подождать или же показать, что денег уже достаточно и можно приступать к варке кофе. То же действие, но другой эффект - в зависимости от того, что было сделано ранее, как и описано в этом задании на примере музыкального инструмента.
Бобр Никита работает на заводе, где воду разливают по бутылкам. Каждый день он должен заполнить наибольшее возможное количество имеющихся бутылок водой, которая хранится в 50-литровой бочке.
Сегодня он должен заполнить 10 бутылок, на которых имеются этикетки с указаниями вместимости воды в литрах:
Каково наибольшее количество бутылок, которые бобр Никита сможет полностью заполнить?
[Tekstikast, täisarv]
Правильный ответ: 7 бутылок.
Если у нас пустые бутылки, куда вмещается различное количество воды, то заполнение большей бутылки нам будет невыгодно. Поэтому для решения задания мы прежде всего должны упорядочить бутылки по их объёму - от маленького к большому:
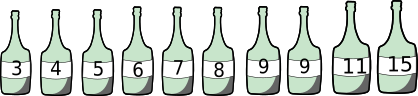
Теперь можем заполнять бутылки водой до тех пор, пока она не закончится. Действуя таким образом, мы сможем полностью заполнить 7 бутылок, израсходовав 3+4+5+6+7+8+9=42 литров воды. После этого у нас останется ещё 8 литров, но любая оставшаяся бутылка вмещает в себя по меньшей мере 9 литров. Таким образом, больше бутылок мы не сможем заполнить.
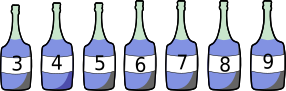
Жадным алгоритмом (greedy algorithm) называют любой алгоритм, который следует используемой при решении задания стратегии, при которой на каждом шагу делается локальный оптимальный выбор. Во многих заданиях жадная стратегия не приводит к оптимальному глобальному решению, но этот алгоритм позволяет за разумный промежуток времени найти локальное оптимальное решение, что является приближённым решением глобального оптимального решения.
У жадного алгоритма есть пять компонентов:
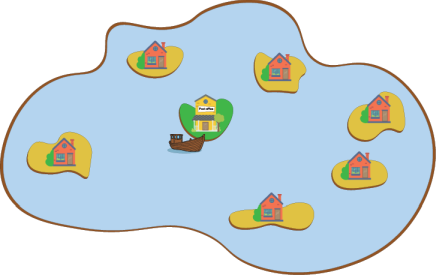
Часть Бобруйска состоит из определённого количества островов, соединённых между собой мостами. Для каждого моста действует ограничение по грузоподъёмности, и грузовик, который превышает это ограничение, не может проехать по мосту.
Ниже приведена карта островов Бобруйска, где острова представлены в форме кружков, а мосты в форме отрезков. Рядом с каждым мостом указано действующее ограничение по грузоподъёмности.
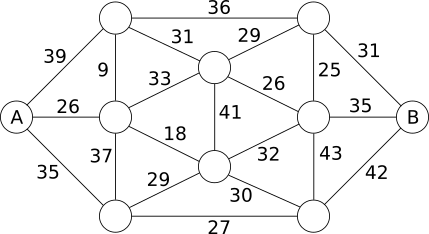
Фирме "Поставки из Бобруйска" необходимо доставить песок с острова А на остров В. Какова будет наибольшая общая масса грузовика, который смог бы добраться с острова А на остров B?
[Raadionupud]
A. 42 тонны
B. 39 тонн
C. 32 тонны
D. 31 тонна
Правильный ответ C. 32 тонны и путь будет следующим:
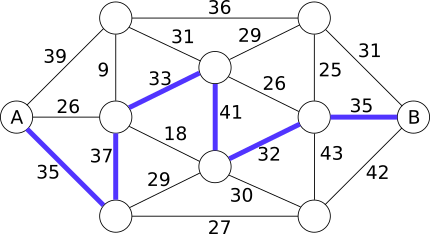
Один из способов найти решение - это начать с тяжёлого веса и посмотреть, по каким мостам можно будет проехать. Если вес будет слишком большим, то мы будем его уменьшать до тех пор, пока не сможем проехать по мостам, которые в итоге приведут нас к острову B.
Можем начать с самого большого веса, который может выдержать один мост - 43 тонны. Такой вес выдерживает только один мост - отметим его:
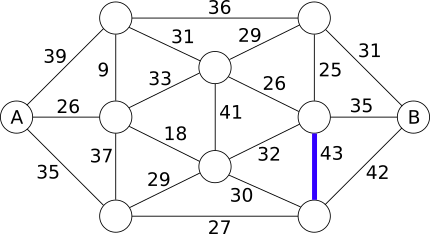
Но это не позволит нам проехать с острова A до острова B. Для прохождения большего количества мостов уменьшим вес до 42 тонн и обозначим этот мост:
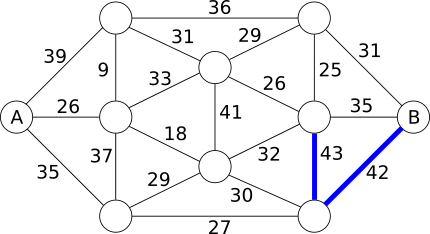
Но это опять не позволит нам проехать с острова А до острова B. Опять уменьшим вес, добавим мосты, которые выдерживают 41 т, затем 39, 37, 36 и 35 т.
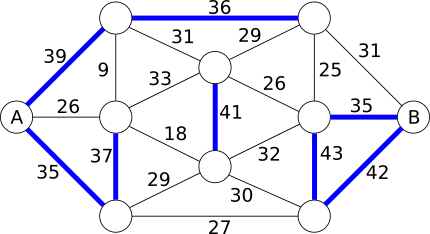
Если вес составит 35 тонн, то мы сможем проехать 8 мостов, но всё равно не сможем проехать с острова А до острова B. Продолжим: выберем вес 33 тонны, затем 32 тонны и получим следующее количество мостов:
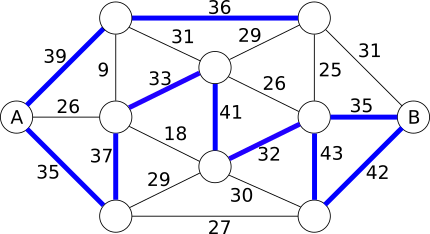
Теперь у нас достаточное количество мостов, чтобы проехать с острова А до острова B. Удалим обозначения тех мостов, которые мы ранее обозначили, но которые мы в итоге не использовали. Итого, правильный путь выглядит следующим образом:
Данное задание является примером задачи о самом широком пути из теории графов. Она применяется, например, при нахождении максимальной пропускной способности сети между заданными пунктами и в других задачах на тему "бутылочного горлышка". Также её можно рассматривать как подчасть в задании на нахождение максимальной пропускной способности, которое используется в алгоритме Форда-Фалкерсона для нахождения максимального потока.
Наш алгоритм схож с алгоритмом Крускала, который используется для поиска наименьшего остовного дерева графа.
На автомобильном заводе занимаются разработкой нового поколения автомобилей. Эти машины отличаются друг от друга за счёт (a) цвета, (b) обшивки салона, (c) покрышек и (d) мотора. Для каждой машины имеется 5 возможностей, которые перечислены в нижеприведённой таблице.
| Цвет | Обшивка салона | Покрышки | Мотор |
|---|---|---|---|
| 0. Синий | 0. Чёрная кожа | 0. Спортивные покрышки | 0. Дизель |
| 1. Красный | 1. Белая кожа | 1. Городские покрышки | 1. Бензин |
| 2. Белый | 2. Чёрный текстиль | 2. Шоссейные покрышки | 2. Гибрид |
| 3. Чёрный | 3. Белый текстиль | 3. Удерживающие покрышки | 3. Природный газ |
| 4. Зелёный | 4. Красный люкс | 4. Люксовые покрышки | 4. Электро |
На заводе всем возможным машинным комбинациям параметров присваиваются номера от 0 до 624.
Сначала номер 0 присваивается модели с комбинацией параметров 0 0 0 0, то есть синяя машина с чёрной кожаной обшивкой салона, со спортивными покрышками и с дизельным мотором. Модель 1 - это машина с комбинацией параметров 0 0 0 1, которые соответствуют синей машине с чёрной кожаной обшивкой салона, со спортивными покрышками и с бензиновым мотором. Модель 2 - это машина с комбинацией параметров 0 0 0 2, а модель 5 - это машина с комбинацией параметров 0 0 1 0.
Например, машина с комбинацией параметров 2 0 1 4 будет белой с чёрной кожаной обшивкой салона, с городскими покрышками и с электромотором. Номером этой модели будет 259.
Какой номер модели будет у зелёной машины с красной люксовой обшивкой салона, люксовыми покрышками и работающим на природном газе моторе?
[Tekstikast, täisarv]
Правильный ответ 623.
Номерами перечисленных параметров являются 4 (зелёный), 4 (красный люкс), 4 (люксовые покрышки) и 3 (природный газ). Записав эти данные друг за другом, получим 4 4 4 3. Это соответствует некоторому числу в пятеричной системе, преобразовав которое в десятичной системе получим 623. Это и будет номером модели... Но как же мы получили это значение?
Из приведённого примера можно заметить, что каждый раз, как только мы увеличиваем номер последнего параметра (тип мотора), то к номеру модели добавляем 1. Ещё более интересно то, что обратившись к спецификации покрышек, к номеру модели мы должны прибавить не 1 (иначе бы это перепуталось при изменении типа мотора), а 5. Почему же 5? Потому что для мотора имеется только 5 возможностей и после них каждый последующий номер модели должен где-то меняться - в данном случае у возможностей покрышек.
Аналогично рассуждая, мы найдём, что перебирая варианты с обшивками салона, мы должны прибавлять к номеру модели 25. Почему же 25? Потому что для двух расположенных с правой стороны параметров имеется 5x5=25 возможных вариантов. По такому же принципу выбор следующего цвета несёт с собой изменение номера модели на 5x5x5=125 единиц.
Теперь мы можем посчитать, сколько раз каждый параметр "обновлён" по отношению к базовым параметрам, и сложить всё вместе, предварительно перемножив их на описанные выше коэффициенты:
(цвет) 4 x 125 + (обшивка салона) 4 x 25 + (покрышки) 4 x 5 + (мотор) 3 = 623.
Есть и другая возможность получить ответ. Обратите внимание, что в изучаемой модели все параметры кроме мотора имеют наибольшее возможное обозначение - только мотор будет иметь второе по величине обозначение. Таким образом, обозначение модели должно быть на единицу меньше максимально возможного:
624 - 1 = 623.
Изменение основы системы счисления очень полезно. Благодаря этому мы можем пересылать информацию, передача которой в десятичной системе была бы затруднительна.
Десятичная система, которую мы ежедневно используем, не является той системой, которая позволяет сохранять в памяти компьютера числа. В компьютерах используется двоичная система: числа состоят только из цифр 0 и 1. Когда ты вводишь в компьютер число, то компьютер преобразовывает его в двоичную систему и выполняет свои вычисления именно с ней.
В действительности, компьютеры хранят все данные в двоичной системе: не только числа, но и, например, звуки, рисунки, фильмы, 3D-модели и так далее.
Бобр Анюта рассылает друзьям сообщения, используя тайный код. Она организовывает частную вечеринку и хочет отправить друзьям пароль 3124, который надо будет сказать охране на входе.
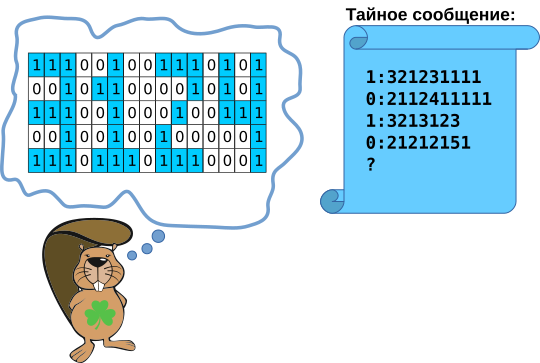
Что будет содержать последняя строчка этого зашифрованного сообщения?
[Raadionupud]
A. 0:3131331
B. 1:321231111
C. 1:3131331
D. 1:231231111
Правильный ответ C.
Первая цифра в каждой строчке сообщения указывает на то, с квадрата какого цвета (белого или синего) начинается соответствующая строчка на рисунке. Обратите внимание, что 0 обозначает белый, а 1 - синий квадрат. Следующие после двоеточия цифры указывают на то, сколько квадратов одного цвета из каждого чередующегося цвета последует.
Последняя строчка на рисунке начинается с синего квадрата (1). За двоеточием следует число, которое указывает на количество квадратов такого цвета (3 синих квадрата). Далее следует 1 белый квадрат, потом 3 синих квадрата, затем 1 белый квадрат и так далее:
| первый квадрат синий | : | 3с | 1б | 3с | 1б | 3с | 3б | 1с |
|---|---|---|---|---|---|---|---|---|
| 1 | : | 3 | 1 | 3 | 1 | 3 | 3 | 1 |
Вариант ответа A не может быть правильным, так как начинается с 0 - это означает, что первый квадрат должен быть белым, как на 2 и 4 строчках на рисунке. Этот вариант описывает строчку на рисунке противоположной той, которую хочет получить Анюта.
Вариант ответа B не может быть правильным, так как они описывает строчку рисунка, которая идентична первой строчке рисунка - после 3 синих квадратов следует 2 белый квадрата и так далее.
Вариант ответа D не может быть правильным, так как в этом случае последняя строчка на рисунке должна была бы начинаться с 2 синих квадратов.
Данное задание связано с несколькими понятиями кодирования данных:
В случае обработки данных обычным делом является то, что для представления одной и той же информации может быть использовано несколько способов и данные необходимо преобразовать из одной формы представления в другую.
В этом задании введённое понятие кодирования длин серий (run-length encoding, RLE) является очень простой формой сжатия данных без потерь. Алгоритм кодирования длин серий применяется к последовательностям, где зачастую одно и то же значение указано несколько раз подряд. Данную последовательность кодируют таким образом, что каждое значение сохраняется только один раз, а за ним записывается, сколько же раз это значение было представлено. В большинстве случаев получаемая величина на выходе будет меньше входной величины, однако в худшем случае может получиться и больше.
В данном задании отказались от сохранения значений, предполагая, что каждое последующее количество раз соответствует значению, которое будет противоположно предыдущему значению. (Сумеешь ли ты найти пример такой ситуации, когда, следуя этому подходу, Анюта зайдёт в тупик? Могут ли такие рисунки встречаться в представлении паролей?)
Для решения данного задания необходимо умение обобщать и мыслить алгоритмически. Прежде всего необходимо вспомнить алгоритм кодирования длин серий и сравнить соответствующие строчки из таблицы и из сообщения. Далее этот алгоритм необходимо применить к последней строчке на рисунке и получить последнюю строчку сообщения.
В конце хотелось бы отметить, что RLE не является сильным алгоритмом криптографии. Если подсмотреть некоторые зашифрованные сообщения, то разгадать алгоритм не составит труда, даже не зная соответствующего пароля. Поэтому не стоит его использовать при шифровании действительно важных тайн.
Для того чтобы открыть замок, необходимо установить четыре цифры в правильном положении. Каждую цифру можно пошагово крутить вперёд или назад.
На рисунке видно, что для замка выбрана комбинация цифр 2719. Цифру 7 мы можем сдвинуть на один шаг вперёд (и получить цифру 8) или назад (и получить цифру 6). Если сдвинуть цифру 9 вперёд, то получим цифру 0. Аналогично, если сдвинуть цифру 0 назад, то получим цифру 9.
Каково наименьшее общее количество шагов необходимо сделать для открытия замка, если сейчас цифры показывают 2719, а открывающий замок код должен быть 4383?
[Raadionupud]
A. 21
B. 19
C. 17
D. 13
E. 12
Правильный ответ D. 13.
Каждую цифру мы можем сдвинуть вперёд или назад, а из этих сдвигов выберем меньшее.
Выбирая для каждой цифры меньшее количество сдвигов, получим: для первой цифры надо сделать два шага вперёд (2→3→4), для второй цифры четыре шага назад (7→6→5→4→3), для третьей цифры три шага назад (1→0→9→8) и для последней цифры четыре шага вперёд (9→0→1→2→3). В итоге, это даст нам 13 шагов.
Неправильные варианты ответов
A. 21 (=2+6+7+6) будет количеством шагов, например, тогда, когда мы будем крутить первую цифру вперёд (2→3→4), вторую цифру вперёд (7→8→9→0→1→2→3), третью цифру вперёд (1→2→3→4→5→6→7→8) и последнюю цифру назад (9→8→7→6→5→4→3).
B. 19 (=2+6+7+4) будет количеством шагов, например, тогда, когда каждую цифру мы будем крутить вперёд, то есть (2→3→4), (7→8→9→0→1→2→3), (1→2→3→4→5→6→7→8) и (9→0→1→2→3).
C. 17 (=2+4+7+4) будет количеством шагов, например, тогда, когда первую цифру будем крутить вперёд (2→3→4), вторую цифру назад (7→6→5→4→3), третью цифру вперёд (1→2→3→4→5→6→7→8) и последнюю цифру вперёд (9→0→1→2→3).
E. 12 будет неверным значением, если мы посчитаем 13 шагов неправильно и получим число меньшее 13.
Это задание представляет собой задачу минимизации количества значений, определённых алгоритмом. Минимизация - это подвид задания на оптимизацию.
В этом задании нам необходимо минимизировать сумму независимых значений. Для достижения этой цели минимизируем каждое значение по отдельности. Обратим внимание, что минимум суммы независимых значений всегда равен сумме минимумов этих значений.
Сами значения определены алгоритмически, так как каждую цифру можно крутить вперёд или назад. Это означает, что для получения цифры 9 из цифры 2 мы можем сделать три шага вперёд (9→0→1→2), а можем и семь шагов назад (9→8→7→6→5→4→3→2). Обратите внимание, что сумма шагов вперёд и назад будет 10, так как это длина цикла.
Таким образом, для каждого числа из количества шагов берём наименьшее, а сумма этих наименьших шагов и будет являться минимумом всей суммы.
Март организовывает ужин для семей бобров. Он пригласил своего друга Роберта и ещё две бобровых семьи: папу и маму Тамм вместе с сыном Генри и дочкой Ритой, а также папу и маму Каск вместе с дочерями Лизой и Дианой.
Чтобы завязалась беседа, Март установил некоторые правила по рассадке участников вокруг стола круглой формы.
Два бобра женского пола не сидят рядом.
Папа и мама из одной и той же семьи не сидят рядом.
Молодые бобры не сидят рядом со своими родителями.
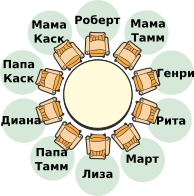
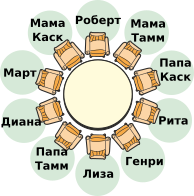
Что из приведённых вариантов будет соответствовать правилам Марта по рассадке участников вокруг стола?
[Raadionupud]
| A | B | C | D |
|---|---|---|---|
 |
 |
 |
 |
Правильный ответ B.
В варианте ответа A мама и папа Каск сидят рядом, а это противоречит правилу №2. К тому же Диана сидит рядом со своим папой, что также противоречит правилу №3.
В варианте ответа C Лиза сидит рядом со своим папой, а это противоречит правилу №3.
В варианте ответа D Диана сидит рядом с мамой Тамм, а это противоречит правилу №1. Рита сидит рядом со своим папой, что также противоречит правилу №2.
В варианте ответа B все правила (условия) соблюдены, поэтому это будет правильным ответом.
Задание по организации стола для ужина на самом деле является простым вариантом задачи на более общие "ограничения". У нас имеется некоторое количество ограничений (правил) и диапазон значений, и мы должны найти решение, которое бы удовлетворяло всем этим ограничениям.
Для достижения этой цели мы должны из имеющихся данных создать модель и затем выстроить решение шаг за шагом. Определим переменные, их возможные значения, действующие ограничения. В данном задании в роли переменных выступают занятые бобрами места.
Далее постараемся найти решение шаг за шагом, по одному присваивая переменным подходящие значения и перенося далее влияние присваивания значения на оставшиеся переменные. Иногда может случиться так, что при присвоении значений возникает сбой. В таком случае мы должны сделать шаг назад, присвоить переменным другие значения и попробовать снова.
В этом задании наша работа проще: значения уже даны в виде вариантов ответа, и нам следует просто проверить удовлетворяют ли они ограничениям или нет.
Следуя приведённым правилам, можно создать красивые орнаменты:
1-ое правило: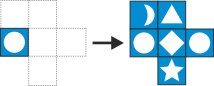 
2-ое правило: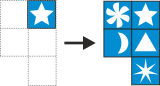 
3-ье правило: 
Например, начав с фигуры 
, мы можем получить фигуру 
, если применим два раза 3-е правило.
Если начать с одного единственного круга (
), то какой из следующих орнаментов можно создать?
[Raadionupud]
A. 
B. 
C. 
D. 
Правильный ответ A.
На следующем рисунке видно, как, начав с одного единственного круга (), можно создать орнамент A. Применим один за другим 1-ое, 2-ое и 3-ье правила:
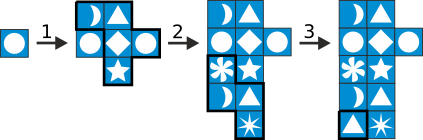
Далее к расположенному с правой стороны кругу (на рисунке отмечен стрелкой) применим 1-ое правило, а затем вновь 2-ое и 3-ье правила.
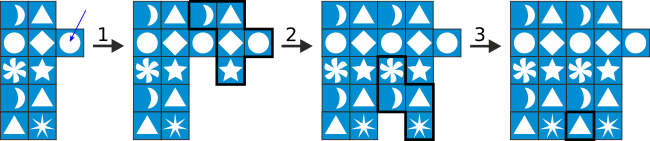
Здесь мы применили правила в следующие порядке 1 2 3 1 2 3, но для получения такого же решения возможен и другой порядок.
Для того чтобы заметить, что другие орнаменты невозможны, нам необходимо воспользоваться "трюком". (Конечно, можно снова и снова пробовать составлять орнаменты B, C и D и при этом никогда не достичь результата. Однако в этом случае мы не можем быть уверены на все 100%, что мы не упустили какую-нибудь возможность или не сделали ошибку...).
Орнамент D невозможен: 1-ое правило - это единственное правило, с помощью которого можно образовать квадрат (
). При этом каждый раз вместе с квадратом будет возникать и круг (
). Если мы начнём с одного круга, то каждый возможный орнамент будет всегда содержать на один больше кругов чем квадратов. В орнаменте D количество кругов равно количеству квадратов. Поэтому, следуя приведённым правилам, создать орнамент D невозможно.
Орнамент B невозможен: 1-ое правило - это единственное правило, которое позволяет создать 5-конечную звезду (
). Эта 5-конечная звезда всегда располагается под квадратом (). Над звездой, расположенной с самой правой стороны орнамента B, нет квадрата. Поэтому, следуя приведённым правилам, создать орнамент B невозможно.
Орнамент C невозможен: аналогично, единственное правило, которое позволяет добавить в орнамент 7-конечную звезду (
) (2-ое правило), также добавляет над ней треугольник (
). Орнамент С содержит 7-конечную звезду, но без расположенного над ней треугольника. Поэтому, следуя приведённым правилам, создать орнамент C невозможно.
Второй (и более короткий) аргумент: из всех приведённый правил только 1-ое правило расширяет орнамент в правую сторону. По этой причине в расположенном справа столбце каждого орнамента должен быть круг (). Однако в орнаментах B, C и D это не так.
Для того чтобы компьютеры могли выполнять свою работу, кто-то (обычно программист) должен сказать компьютеру в той или иной форме, что точно необходимо выполнить. Часто это говорится компьютеру с помощью написания программы, но иногда программист может просто задать множество правил, которым компьютер должен следовать. В этом задании мы так и сделали. На практике правила обычно записываются в виде текста и их не объясняют с помощью рисунков. Но, кто знает, может в будущем, когда компьютеры станут умнее, будет достаточно просто нарисовать необходимые действия...
Информатика занимается не только тем, как записать правила для компьютера. Некоторые учёные исследуют также, какие правила лучше использовать, что будет возможным или нет при соблюдении этих правил. Часто они используют такие же трюки, как и мы, когда объясняли, почему невозможно создать орнаменты B, C и D. И действительно, часто в этих трюках применяется счёт или математика. (Эту часть в информатике называют теоретической информатикой.)
Во время каникул в течение двух недель Марина помогала маме в их домашнем кафе.
Утром каждого понедельника она получила от мамы монеты на сумму 40€. Так как эти монеты предполагалось использовать для того, чтобы давать сдачу, то девочка положила их в кассу.
В конце каждого рабочего дня она записывала, сколько денег уже находится в кассе. Основываясь на собранных данных, она построила график:
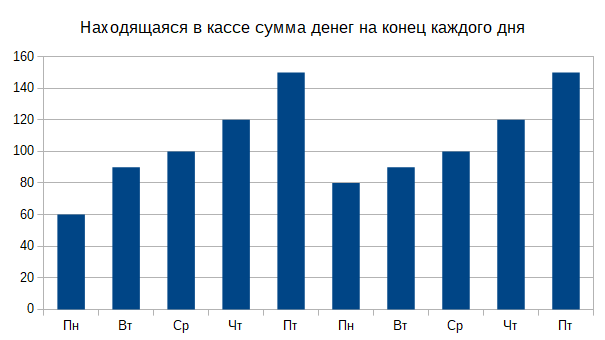
Вечером каждой пятницы она забирала все деньги из кассы и передавала их маме.
Какая была самая большая дневная выручка в евро?
[Tekstikast, täisarv]
Правильный ответ 40€.
Для получения лучшего обзора о доходе кафе построим график. На нём отдельно отметим, что было в кассе каждое утро и каждый вечер (помним, что утром каждого понедельника к первоначальной сумме добавлялось 40€):
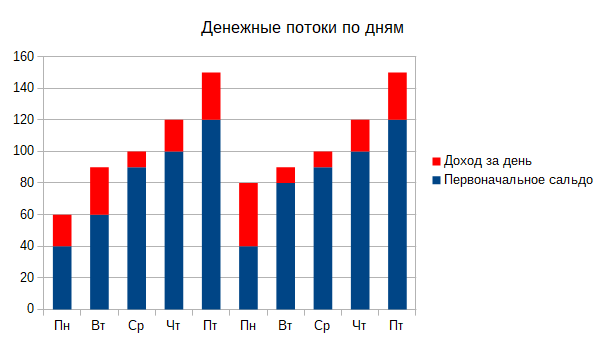
Картина будет более понятной, если с графика уберём данные о состоянии кассы на утро каждого дня и сосредоточимся на доходе, который кафе получало в течение дня:
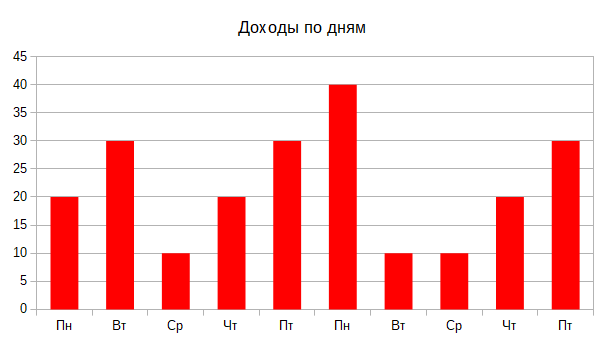
Теперь очевидно, что самая большая дневная выручка была 40€. Эту выручку кафе получило на второй неделе в понедельник.
Данное задание демонстрирует, как способ представления данных может облегчить или усложнить поиск ответа на вопрос. Если используемые для построения графика данные находятся в электронной таблице или базе данных, то необходимые преобразования для лучшего представления данных нам поможет выполнить компьютер. Чем больше данных, тем больше пользы будет от такого автоматического преобразования.
Для поиска слов в тексте можно использовать регулярные выражения (regular expressions). Они могут содержать метасимволы, с помощью которых задают более сложные правила поиска.
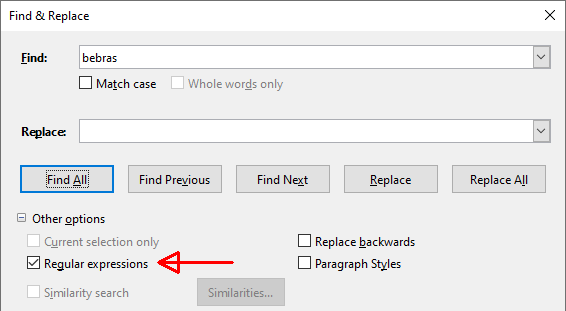
Вот некоторые из метасимволов:
[:space:] – пробелы, например b[:space:]e найдёт текст b e,
? – специальный символ, указывающий, что знак перед ним может в тексте встречаться или отсутствовать, например be?b найдёт beb, а также и bb.
В приведенном ниже тексте слово "bebras" встречается пять раз (выделены жирным шрифтом), и каждый раз оно записано по-разному:
There are two extant species of b-e-b-r-a-s; the North American b e b r a s and the Eurasian bebras. The American bebras was coined by Carl Linnaeus in 1758 who also classified the species name fiber. However, the two bebas were not conclusively shown to be separate species until the 1970s with chromosomal evidence.
Какое регулярное выражение следует ввести в окно поиска, чтобы найти в тексте все пять вариантов слова "bebras"?
[Raadionupud]
A. _?b-?e-?b-?r?-?a-?s_?
B. _?b-?[:space:]?e[:space:]?-?b[:space:]?-?r?[:space:]?-?a[:space:]?-?s_?
C. _?b[:space:]?e[:space:]?b[:space:]?r?[:space:]?a[:space:]?s_?
D. _?b-?[:space:]?e[:space:]?-?b[:space:]?-?[:space:]?-?a[:space:]?-?s_?
Правильный ответ B. _?b-?[:space:]?e[:space:]?-?b[:space:]?-?r?[:space:]?-?a[:space:]?-?s_?.
Рассмотрим каждое выражение по отдельности.
Выражение А не найдёт вариант "b e b r a s", где между буквами имеются пробелы:
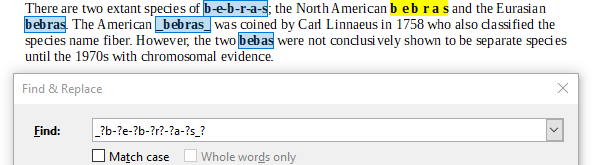
Выражение B найдёт все пять вариантов:
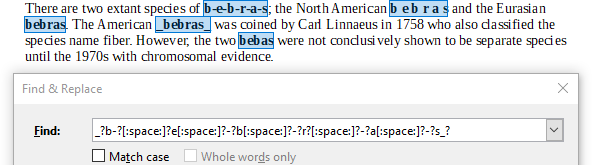
Выражение С не найдёт форму слова со знаком дефиса между буквами:
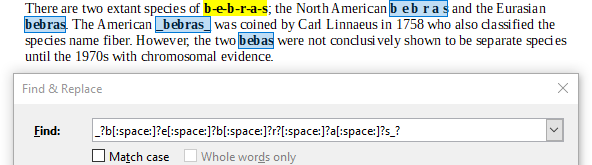
Выражение D найдёт только вариант с пропущенной буквой "r":
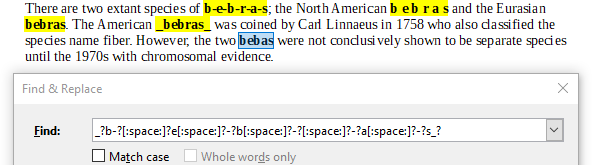
Регулярные выражения очень часто используются в программировании, например, для поиска совпадающих символов, множества символов, слов. Также они используются для валидации целых строк, поиска и замены слов или символов. Регулярные выражения также можно использовать для валидации данных, например, когда паролю задаются требования в виде минимального количества символов или наличия маленьких и больших букв, цифр или специальных символов.
Бобру Тому захотелось запечатлеть на одной фотографии всех своих друзей в лесу. Для этого он решил сделать панорамную фотографию, комбинируя несколько маленьких фотографий. Позже все эти маленькие фотографии объединяются в одно целое, и создаётся одна панорамная фотография. Здесь представлены все сделанные им фотографии:
Сколько бобров будет на панорамной фотографии?
[Tekstikast, täisarv]
Правильный ответ 7.
Эти фотографии поменьше получены из одной большой фотографии. Как видим на приведённом ниже панорамном рисунке, на нём запечатлено 7 бобров.
Наверняка, вы уже изучили возможности своих камер и смартфонов, в том числе и возможность делать панорамные снимки. Это позволяет объединять несколько фотографий в одну большую. По этой причине это также является частью информатики.
По случаю дня рождения бабушки-бобра к ней приехали все её 5 внуков. В виде подарка они принесли настольную игру на 4 человека и пообещали по воскресеньям навещать бабушку почаще, начиная с сегодняшнего воскресенья:
Какая состоящая из трёх бобров-детей группа соберётся первой после дня рождения бабушки, чтобы вновь сыграть с ней в настольную игру?
[Raadionupud]
A. Альберт, Боря, Василиса
B. Василиса, Галя, Денис
C. Боря, Василиса, Денис
D. Альберт, Василиса, Галя
Правильный ответ C (Боря, Василиса, Денис), которые встретятся через 24 недели.
Два бобра X и Y, которые навестят бабушку через fX и fY недель, вновь встретятся друг с другом через НОК(fX, fY) недель, где НОК обозначает наименьшее общее кратное.
Такой подход можно расширить и на трёх бобров: НОК(fX, fY, fZ) = НОК(НОК(fX, fY), fZ).
Задание можно решить с помощью нахождения наименьшего общего кратного. С помощью алгоритмов для нахождения наименьшего общего кратного и наибольшего общего делителя можно решать различные задания, в которых необходимо выяснить, насколько разные части подходят друг другу. Примеры таких заданий можно найти в различных областях - от астрономии (противостояние планет) до криптографии.
Пространство для хранения данных на жёстком диске разделено на кластеры определённого размера. При сохранении файл всегда занимает целое число кластеров. Если размер файла не делится на размер кластера, то часть последнего занятого файлом кластера просто остаётся неиспользованной.
На приведённом рисунке изображено использование жёсткого диска, поделённого на кластеры размером 16 KB - использованные кластеры обозначены серым цветом, а пока ещё свободные кластеры - белым.
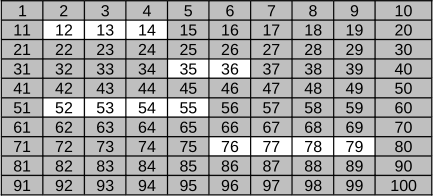
На диск по одному записываются следующие файлы: прежде всего файл A размером 20 KB, затем файл B размером 18 KB, потом файл C размером 34 KB и наконец файл D размером 48 KB. Во время сохранения файла операционная система старается найти свободные кластеры, которые бы располагались один за другим. Это делается с целью избежать фрагментации файлов, то есть распределения файла между разными частями диска, что уменьшает продуктивность компьютера.
Один из подходов для уменьшения фрагментации файлов заключается в следующем.
Найти набор расположенных один за другим свободных кластеров, куда поместился бы весь файл.
Если такого набора нет, то распределить файл таким образом, что имеющиеся куски можно было бы расположить в первые попавшиеся кластеры.
Как выглядит файловая система после того, как по описанным выше правилам записываются файлы A (красный), B (зелёный), C (синий) и D (жёлтый)?
[Raadionupud]
A.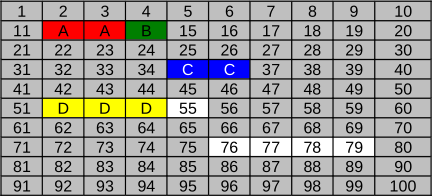 
B.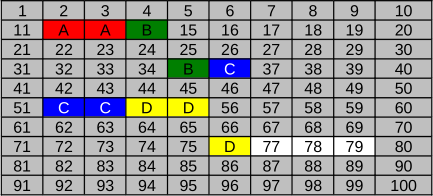 
C.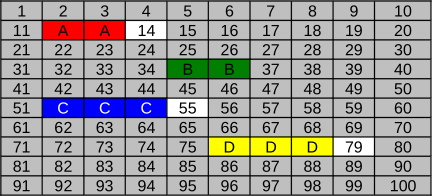 
D.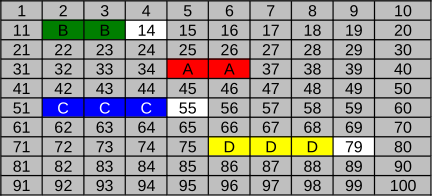 
Правильный ответ C.
Файл A (20 KB) записывается в кластеры 12 и 13 (в них имеется 32 KB свободного места).
Файл B (18 KB) записывается в кластеры 35 и 36 (в них имеется 32 KB свободного места). Кластер 14 останется неиспользованным, так как его использование привело бы к фрагментации файла B. Использовав кластеры 35 и 36, мы избежим этой проблемы.
Файл C (34 KB) записывается в кластеры 52, 53 и 54 (в них имеется 48 KB свободного места).
Файл D (48 KB) записывается в кластеры 76, 77 и 78 (в них имеется 48 KB свободного места).
Вариант А не будет правильным ответом. Согласно этому варианту, файл B займёт только один кластер. Так как размер кластера равен 16 KB, то невозможно в один кластер уместить файл размером 18 KB. Аналогично, нельзя уместить файл C в два кластера.
Вариант B не будет правильный ответом. Согласно этому варианту, при сохранении файл B был фрагментирован - однако, следуя правилу №1, этого делать нельзя, если найдётся некоторое количество свободных расположенных друг за другом кластеров с достаточным размером. Аналогично, файлы C и D были бы бессмысленно фрагментированы.
Вариант D не будет правильным ответом. Согласно этому варианту, файл A сохранили в кластеры 35 и 36, хотя на момент записи кластеры 12 и 13 были свободны. Следуя правилу №1, файл А следовало записать в первую область с подходящим размером.
Данное задание демонстрирует нам, как хранится информация на жёстком диске, и объясняет, что же такое фрагментация файлов.
В примере этого задания мы уже видим, что начальное состояние файловой системы подверглось внешней фрагментации. Это привело к тому, что на диске мало расположенных рядом друг с другом свободных кластеров. Внешняя фрагментация возникает тогда, когда создаются, изменяются или удаляются файлы различных размеров.
Когда создаётся один большой файл, а на диске нет достаточного количества свободных расположенных рядом друг с другом кластеров, то файл дробится на маленькие части, которые затем записываются в файловую систему. Этот процесс называется фрагментацией файла. Минусом такого процесса является уменьшение продуктивности жёсткого диска.
Третий тип фрагментации встречается в управлении оперативной памятью (RAM) компьютера. Оперативная память также разделена на страницы с определённым размером, и её распределение между программами также происходит по страницам. Обычно программа использует несколько страниц, причём зачастую последняя страница не бывает заполнена до конца. В результате в памяти остаётся свободное пространство, которым другие программы, к сожалению, не могут воспользоваться. Это называется внутренней фрагментацией.
Copyright © 2020 Bebras – International Challenge on Informatics and Computational Thinking.
Licensed under Creative Commons Attribution-ShareAlike 4.0 International License.
Flag icons by GoSquared.