

Doktor Kobraste teab, et üks tema 16 patsiendist on nakatunud. Tal on ainult 8 katseklaasi, A, B, C, D, E, F, G ja H. Nakatunud kopra ülesleidmiseks on tal vaja saada vereproov, milles esineb nakkus. Ta võtab igalt kopralt proovi ja segab osa proove tähistatud katseklaasides kokku teiste kobraste proovidega. Ta järgib hoolikalt proovide jaotusplaani:
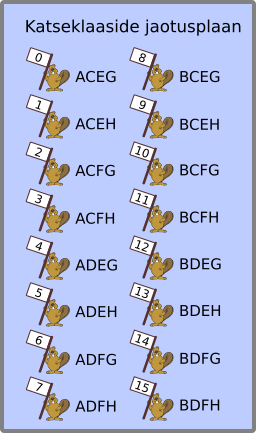
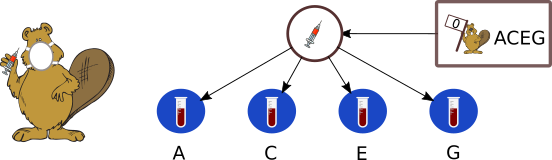
Näiteks kopra number 0 vereproov jaotatakse katseklaasidesse A, C, E ja G:
Praeguseks on doktor Kobraste testinud katseklaase A (nakatunud), C (terve) ja E (terve).

Millist neist 4 katseklaasist peaks doktor Kobraste järgmisena testima, et nakatunud kobras üles leida?
[Raadionupud]
Katseklaas B
Katseklaas D
Katseklaas F
Katseklaas G
Õige vastus on 4. Katseklaas G.
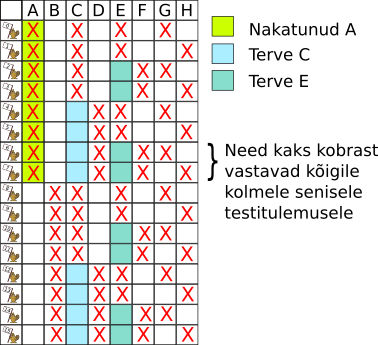
Seniste testide põhjal on nakatunud kobras kas 6 või 7. Katseklaasis G on kopra 6 verd, aga ei ole, kopra 7 oma; katseklaasis H, vastupidi, on kopra 7 verd, aga ei ole kopra 6 oma. Kuna me teame, et nakatunud on täpselt üks kobras, siis katseklaasi G või H testimine (tulemuseks saame kas nakatunud või terve) võimaldab meil määrata, kumb neist kahest koprast nakatunud on. Seega pakutud variantide hulgast on õige vastus katseklaas G.
Katseklaaside B, D ja F testimise tulemused ei sõltu sellest, kas nakatunud on kobras 6 või 7 (katseklaasis B on mõlemal juhul ainult terve veri; katseklaasides D ja F on mõlemal juhul nakatunud verd). Seega nende katseklaaside testimine doktor Kobrastet edasi ei aitaks.
Rühmatestimine on tehnika, millele pani alguse Richard Dorfman vereproovide testimisega teise maailmasõja ajal. Sellest ajast saadik on seda tehnikat peale bioloogia rakendatud ka paljudes teistes valdkondades, näiteks tehnikas ja informaatikas, iseäranis seoses rikete tuvastamisega.
Rühmatestimiseks on olemas mitmeid algoritme. Milline neist on kõige parem, oleneb lahendatava probleemi iseärasustest. Lugeja jaoks, kes tunneb kahendotsimist, on uurimiseks hea lähtepunkt üldistatud kaheksjagamise algoritm.
Näites toodud katseklaaside jaotus lähtub tegelikult kobraste numbrite kahendesitusest (0=0000_2, 1=0001_2, ..., 15=1111_2), kus A, C, E, G on kõik 0 ja B, D, F, H on 1.

Kiigetehasesse saabus uus laadung palke, mis on kõik pikemad kui 1 m.
Tehas tahab valmistada selliseid kiikesid:

Täpsemalt peavad kiikede istmepalgid olema sellised:
Tehases on neli robotit, mis võivad töötada paralleelselt:
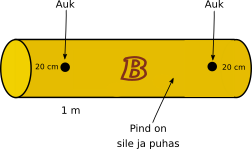
Lõikaja lõikab palgi ühe otsa ära nii, et palgi pikkuseks jääb 1 m.
Koorija eemaldab palgilt koore ning teeb pinna siledaks ja puhtaks.
Puurija puurib palki augud täpselt 20 cm kaugusele vasakust otsast ja täpselt 20 cm kaugusele paremast otsast.
Printija prindib sileda ja puhta palgi keskele ettevõtte logo.
Iga robot töötleb ühte palki korraga ja igal robotil kulub ühe palgi töötlemiseks täpselt üks minut. Robot peab töötlema palki üksinda, ilma et mõni teine robot veel samal ajal selle palgi kallal töötaks. Kui kõik palgid on töödeldud, siis robot peatub.
Robot alustab tööd siis, kui ta saab juhtprogrammilt stardisignaali. Robotit ei tohi käivitada, kui pole palke, mis oleks töötluseks valmis. Juhtprogrammi käsud käivitatakse üksteise järel.
Meil on ette valmistatud 4 juhtprogrammi. Ühes neist töötab iga robot ainult palkidega ja nii kaua aega, kui vaja. Millises?
[Raadionupud]
A. 
B. 
C. 
D. 
Õige vastus on A.
Lõikaja ja koorija töötavad kõigepealt samal ajal ning puurija ja printija alustavad tööd pärast seda, kui esimesed kaks robotit on töötamise lõpetanud. Seda sellepärast, et neil on vaja palke, mis on täpselt 1 m pikad. Printijal on lisaks vaja palke, mis on sileda ja puhta pinnaga.
Ootamiskäsust eespool olevaid käivituskäske võib omavahel ümber järjestada ilma programmi tööd mõjutamata, samuti võib omavahel vahetada ootamiskäsku järel olevaid käivituskäske.
Vastusevariandis B töötab printija enne koorijat. Vastusevariandis C töötab printija enne lõikajat ja seega ei "tea", kus on kiige keskkoht. Vastusevariandis D töötavad printija ja koorija samaaegselt, mis tähendab, et mõne palgi töötleb ikkagi printija enne.
See ülesanne illustreerib paralleelarvutuse kahte põhitehnikat: 1) teisendamist ja 2) protsesside sünkroonimist.
Teisendamine on itereerimise alternatiiv. Defineerime funktsiooni ja teisendame selle abil objektide hulka. See tähendab, rakendame funktsiooni hulga igale elemendile, aga pole oluline, millises järjekorras. Et funktsiooni võib täita paralleelselt mitmel protsessoril, siis on teisendamine kiirem kui itereerimine. Näide Pythonis:
>>> puuviljad = ['pirn', 'apelsin', 'kirss']
>>> s = map(str.upper, puuviljad)
>>> print(list(s))
['PIRN', 'APELSIN', 'KIRSS']Siin teisendatakse sõnede järjendit sõnemeetodi upper() abil.
Ülesande robotid võivad töötada palkide hulgal paralleelselt. Juhtprogramm jälgib, et puurija ja printija ei alusta enne, kui lõikaja ja koorija on töö lõpetanud. Seda nimetatakse protsesside sünkroonimiseks. Ka arvutis tuleb jälgida, et mitu samadel andmetel töötavat programmi üksteist ei segaks.

Koprad soovivad oma külmi maju soojendada kütteelementidega. Nende majad koosnevad kambritest.
Kütteelement võtab enda alla ühe kambri ja soojendab selle kambri kohe üles. 1 minuti jooksul levib kuum õhk soojast kambrist kõigisse selle naaberkambritesse (kambrid, millel on mõne sooja kambriga ühine nurk ja/või sein).

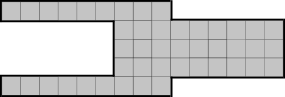
Ülaloleval joonisel on näidatud, mitu minutit kulub väiksema maja iga kambri ülessoojendamiseks, kui kütteelement paigutatakse sinisesse kambrisse.
Aita kobrastel paigutada 4 kütteelementi alloleval joonisel kujutatud suuremasse majja nii, et terve maja soojendataks üles võimalikult kiiresti.
Kui kaua aega kulub terve surema maja ülessoojendamiseks?
[Raadionupud]
A. 1 min
B. 2 min
C. 3 min
D. 4 min
Õige vastus on B. 2 min.
Kui kütteelemendid on paigutatud nii, nagu joonisel, siis kulub kõigi kambrite ülessoojendamiseks 2 minutit.
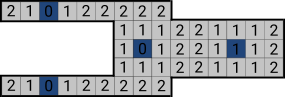
1 minutiga ei ole võimalik kõiki kambreid üles soojendada. Tõepoolest, selleks, et terve maja minuti jooksul üles soojendada, peaksid kõik kambrid asuma kütteelementide vahetus naabruses. Majal on 36 kambrit, seega peaks iga kütteelement olema ühendatud 9 erineva kambriga (kaasa arvatud tema ise), aga see pole maja kuju tõttu võimalik. Või teine võimalus: näeme, et majas leidub järjestikuste kambrite ahelaid pikkusega 15. Et iga kütteelement võib "katta" maksimaalselt 3 kambri pikkuse ahela, siis ei suuda 4 elementi sellist ahelat "katta". Seega vähim aeg on 2 ja õige vastus on B.
See ülesanne on seotud info levimisega graafil, mis siin on maja mudeliks. Iga kambrit esitab üks tipp ja kaks tippu on ühendatud servaga, kui vastavad kambrid on naabrid, nagu ülesande tekstis defineeritud. Selles ülesandes peame välja valima tipud (kambrid), kust pääseb (kuuma õhuga) kõikidesse graafi tippudesse (kambritesse) vähima arvu servade (naaberkambrite) kaudu.

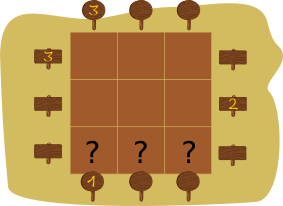
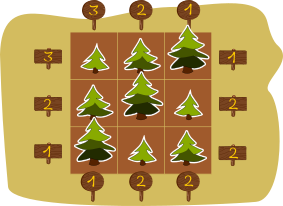
Koprad istutavad väljale ridadena üheksa puud nii, et need moodustavad kolm rida, igaühes kolm puud. Puud on kolme erineva pikkusega:  ,
,  ja
ja  . Igas reas ja igas veerus on igast kõrgusest täpselt üks puu (s.t üheski reas ega veerus ei ole kahte sama kõrget puud).
. Igas reas ja igas veerus on igast kõrgusest täpselt üks puu (s.t üheski reas ega veerus ei ole kahte sama kõrget puud).
Koprad vaatavad igast välja kõrval olevast asukohast (alloleval joonisel), mitu puud on sellest asukohast nähtavad, ja kirjutavad selle arvu märgi peale (märk  tähistab veerge ja märk
tähistab veerge ja märk  ridu):
ridu):

Kui kobras vaatab samal joonel asuvaid puid, siis ta ei näe neid puid, mis jäävad kõrgemate puude taha:

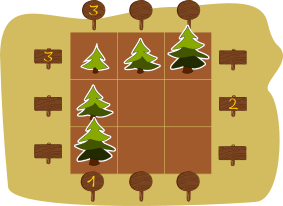
Kui arvud on sellised, nagu alloleval joonisel, siis milline järgmistest variantidest sobib alumiseks reaks (vasakult paremale)?
[Raadionupud]
A. 


B. 


C. 


D. 


Õige vastus on B.
Kaks "kolme" on piisavad selleks, et üheselt taastada kogu väli.
Kui mingist kohast paistavad kõik puud, siis peavad puude pikkused olema järjestatud pikkuse kasvamise järjekorras  ,
,  ,
,  sellest kohast eemale. Niimoodi saame paika panna esimese rea ja esimese veeru:
sellest kohast eemale. Niimoodi saame paika panna esimese rea ja esimese veeru:
Et igas reas ja veerus võib olla igast pikkusest ainult üks puu, siis peab alumise rea keskmises ruudus olema  , sest sest keskmises veerus esineb juba
, sest sest keskmises veerus esineb juba  ja alumises reas
ja alumises reas  . Ja siis peab alumise rea parempoolses ruudus olema
. Ja siis peab alumise rea parempoolses ruudus olema  , sest
, sest  ja
ja  on alumises reas juba olemas.
on alumises reas juba olemas.
Tegelikult on ka ülejäänud puude paigutamiseks ainult üks võimalus:
See ülesanne kasutab kahte informaatika põhioskust. Esimene on oskus leida ülesandele lahendus, mis rahuldab antud tingimust. Teine on võime taastada objekt osalise informatsiooni põhjal, kasutades teadmisi nimetatud objekti omaduste kohta. Seda võib kasutada objekti esituse kokkusurumiseks. Informaatikas kasutatakse selle protsessi kirjeldamiseks mõistet kadudeta pakkimine, sest kasutajal ei lähe informatsioon kaotsi, kui informatsioon lahti pakkida.

Osa Kopramaast koosneb teatud arvust sildadega ühendatud saartest. Igal sillal on kogumassi piirang ning sõiduk, mille mass piirangut ületab, ei või sillast üle sõita. Sõiduki kogumass on sõiduki enda ja tema veetava kauba masside summa.
All on kujutatud Kopramaa saarte kaart, kus saari esitavad ringid ja sildu lõigud. Iga silla juurde on kirjutatud tema kogumassi piirang.

"Kopramaa Tarned" on kauba kohaletoimetamise ettevõte, kus on kasutusel veokid massiga 10 tonni ja kauba maksimaalse massiga 30 tonni.
Milline on vähim saadetiste arv, millega saab viia 250 tonni liiva saarelt A saarele B, kasutades ainult ühe veokit?
[Raadionupud]
A. 10
B. 11
C. 12
D. 13
Õige vastus on C.
Arvutame vastuse kahes etapis. Esmalt leiame, milline on maksimaalne kauba mass, mida veok saab viia ühe sõiduga saarelt A saarele B (olgu see mass x). Teisel etapil arvutame, mitu sõitu peab veok saarelt A saarele B tegema, et kogu liiv ära vedada.
Suuruse x leidmiseks arvutame suurima laadungi, mida saab vedada ühe sõiduga saarelt A muule saarele. Laadung koosneb veoki kaalust ja kauba kaalust. On ilmne, et suurim laadung, mida saab viia saarele A (st jääda saarele A) on 10 t + 30 t = 40 t. Jätkame ahnel viisil, see tähendab, püüame viia järgmisele saarele võimalikult suure laadungi. Meil on järgmine olukord:
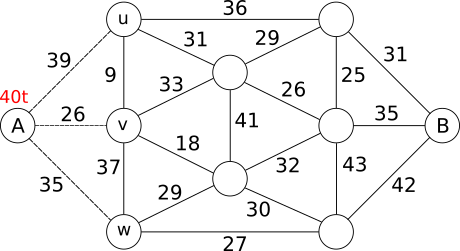
Saarel A on 40 t ja seda võib vedada punktiiriga tähistatud sildade kaudu saartele u, v ja w. Ahne lähenemine soovitab viia laadungi üle suurima kandevõimega silla saarele u, aga silla massipiirangu tõttu saame vedada ainult 39 t. Jõuame olukorrani:
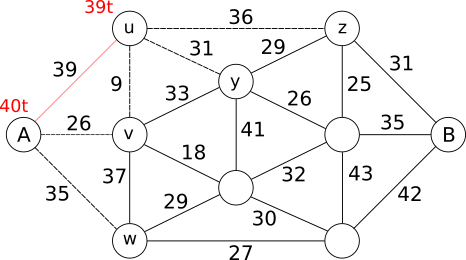
mis ütleb, et suurim laadung, mille saab ühe sõiduga saarelt A minema vedada, on 39 t. Nüüd uurime, millisele saarele peaksime laadungi edasi viima. Vaatluse all olevad saared on ühendatud jälle punktiiriga tähistatud sildade abil, need saared on w, v, y ja z. Saarelt A võime viia saarele v 26 t või saarele w 35 t või saarelt u saarele y 31 t või saarele z 36 t. Et me oleme endiselt ahned, otsustame, viia 36 t saarele z ning meil on järgmine olukord:
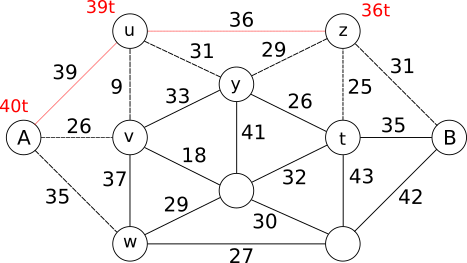
Nüüd teame, et suurim laadung, mille me saame viia ühe sõiduga saarele A on 40 t (ilmne), saarele u 39 t ja saarele z 36 t. Selles olukorras võime vaadelda, jällegi punktiiriga tähistatud sildu silmas pidades, saari w - 35 t saarelt A, v - 26 t samuti saarelt A, y - 31 t saarelt u, t - 25 t saarelt z ja B - 31 t samuti saarelt z. Kuigi võiksime võtta saare B, sest see on meie lõppsiht, järgime ikkagi oma ahnet filosoofiat ja võtame saare w.
Me ei kirjelda siin selgituses kõiki samme, joonistame ainult lõppolukorra:
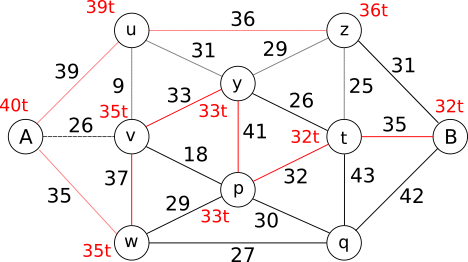
Jooniselt näeme, mis on kõige suuremad laadungid, mida me saame vedada ühe sõiduga saarelt A igale teisele saarele, ja milliseid sildu me peame läbima. Saare q juures laadungi suurus puudub; meil pole seda vaja arvutada, sest me juba jõudsime saarele B. Kokkuvõttes saame, et suurim laadung, mida me saame vedada saarelt A saarele B ühe sõiduga, on 32 t läbi saarte w, v, y, p ja t. Järelikult on suurim veetav kaubakogus 22 t, sest 10 t moodustab veoki kaal. Sellega on esimene etapp lõppenud ning oleme saanud, et maksimaalne kaubakogus, mida veok saab ühe sõiduga vedada saarelt A saarele B, on x = 22 t.
Teises etapis tuletame meelde, et vedada on vaja 250 t liiva. Kümne veokisõiduga saame ära vedada 220 t ja üheteistkümnega 242 t. See jätab meile viimaseks, 12. sõiduks 8 t. Seega vastus on 12 sõitu.
Need, kes tunnevad ülemise täisosa funktsiooni (⌈⌉), võivad vastuse arvutuse kirjutada ka kujul ⌈250 t / 22 t⌉ = ⌈11,36...⌉ = 12.
Antud ülesanne on näide kõige laiema tee ülesandest graafiteoorias. Selle rakendused on näiteks võrgu maksimaalse ribalaiuse leidmine antud otspunktide vahel ja muud "pudelikaela" ülesanded. Seda võib vaadelda ka kui maksimaalse läbilaskevõime leidmise ülesande alamülesannet Fordi-Fulkersoni maksimaalse voo algoritmis.
Paari täiendusega saab meie ahnest algoritmist sisuliselt Primi algoritm vähima toespuu leidmiseks. Peamine täiendus on ühel sammul vaadeldavate punktiirsildade arv. Näiteks pöördudes tagasi teise olukorra juurde, kus me saime teada, et saarele u saab viia maksimaalset 39 t suuruse laadungi, vaatlesime kahe silda saarele v: saarelt A või saarelt u. Seda liiasust võime vältida, kasutades andmestruktuuri, mille nimi on eelistusjärjekord, ning hoida seal ainult paremat neist kahest valikust.

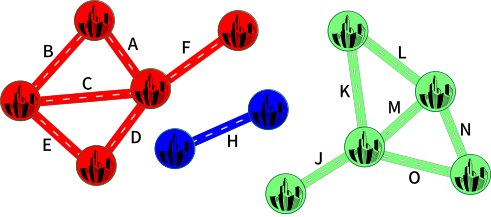
Kaare majapidamises on viis kodumasinat: arvuti, pesumasin, teler, kohvimasin ja tolmuimeja. Nende masinate juhtimiseks on viis nuppu: A, B, C, D ja E.
Kuid nupud pole eriti mugavad. Et nupud on ühendatud mitme masinaga, siis lülitab iga nupp korraga sisse või välja mitu masinat. Täpsemalt muudab nupuvajutus kõigi selle nupuga ühendatud masinate olekud vastupidiseks: mis oli enne väljas, lülitub sisse; mis oli enne sees, lülitub välja.
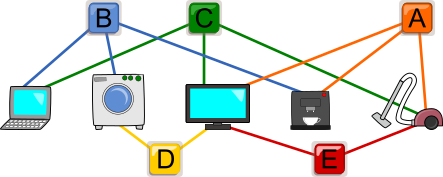
Milline on õige nuppude järjekord, et lülitada sisse ainult teler ja kohvimasin?
[Raadionupud]
Õige vastus on 4. B, D, C, E.
Vajutades nuppu B, lülituvad sisse arvuti, pesumasin ja kohvimasin.

Edasi, vajutades nuppu D, lülitub pesumasin välja ning teler sisse.

Seejärel, vajutades nuppu C, lülituvad arvuti ja teler välja ning tolmuimeja sisse.

Lõpuks, vajutades nuppu E, lülitub teler sisse ja tolmuimeja välja.

Sellel hetkel on teler ja kohvimasin sisse lülitatud ning kõik ülejäänud masinad on välja lülitatud.
Lihtne viis näha, et see vastusevariant on õige ning ülejäänud valed, on vaadata iga nuppu ja masinat eraldi. Näeme, et kui nuppu vajutatakse paaritu arvu kordi, siis saavad nupuga ühendatud masinad lõpuks sisse lülitatuks. Kui aga nuppu vajutatakse paarisarv kordi, siis jäävad masinad välja lülitatuks. Sama kehtib ka iga üksiku masina kohta: kui sellega ühendatud nuppe vajutatakse paaritu arv kordi, siis lülitub masin sisse, paarisarvu vajutuste puhul aga jääb lõpuks välja lülitatuks.
See annab meile järgmise analüüsi.
Esimese jada (E, C, B, A) puhul näeme näiteks, et tolmuimeja on ühendatud kolme vajutatud nupuga (E, C, A). Seetõttu jääb tolmuimeja sisse lülitatuks, mis pole see, mida vaja.
Teise jada (C, B, A, D) puhul näeme, et kohvimasin on ühendatud ainult kahe vajutatud nupuga (B, A), mis tähendab, et ta jääb välja lülitatuks, mis jällegi ei sobi.
Lõpuks, kolmanda jada (D, A, E, C) puhul on näiteks pesumasin ühendatud ainult ühe vajutatud nupuga (D), mis tähendab, et ta jääb sisse lülitatuks, mida pole vaja. Õieti, sisse lülitatuks jäävad kõik masinad peale teleri.
Sama arutluskäik kehtib loomulikult ka õige vastusevariandi (B, D, C, E) puhul, kus nuppude vajutuste arvud on järgmised.
Me võime selle ülesande masinaid ette kujutada kui numbreid, mis suurenevad iga kord, kui vajutatakse nendega ühendatud nuppu. Kuid meie juhul loendavad numbrid ainult kuni üheni, misjärel alustavad uuesti nullist.
See on kahendsüsteem, mida kasutatakse arvutites, kus kogu informatsiooni hoitakse ja töödeldakse ainult kahe numbri, 0 ja 1 abil. Näiteks liitmise sooritamiseks liidab arvuti korraga ühe kahendkoha numbrid ja iga kord, kui tulemus on suurem kui 1, kannab ülejäägi järgmisele kahendkohale, nagu illustreeritud järgnevas tabelis:
| A = 0 1 | A = 0 0 | A = 0 1 |
| B = 0 1 | B = 1 1 | B = 1 0 |
| A + B = 1 0 | A + B = 1 1 | A + B = 1 1 |
Selles ülesandes huvitab meid siiski ainult numbrite liitmine (ülekannet ignoreerime), kusjuures numbrid kirjeldavad masina olekut (1 = sees, 0 = väljas). Seega igal nupuvajutusel liidame masina senisele olekule (0 või 1) ühe:
0 + 1 = 1
1 + 1 = 0

Kopramaal on 12 linna, mis on omavahel ühendatud maanteedega (tähistatud tähtedega A kuni O), nagu näidatud kaardil:
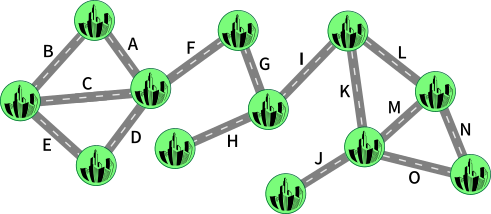
Linnad, mis on omavahel ühendatud kas otse või kaudselt ühe või mitme maantee abil, moodustavad majandusüksuse. Praegu kuuluvad kõik 12 linna samasse majandusüksusesse.
Epideemiapuhangu tõttu aga otsustasid linnapead linnadevahelise reisimise vähendamiseks sulgeda kaks maanteed. Linnapeade eesmärk on jagada kogu maa kolmeks eraldiseisvaks majandusüksuseks. Soovides vähendada majanduse segipaiskamist, peaks kõige väiksem nendest kolmest majandusüksusest sisaldama võimalikult palju linnu.
Millised kaks maanteed tuleb sulgeda?
[Tekstikast, 2 tähte]
Õige vastus on F ja I.
Mõnda maanteed võib ignoreerida, sest nende sulgemine majandusüksust ei tükelda. Näiteks kui sulgeda maantee C, siis saavad elanikud ikkagi reisida maanteede A ja B kaudu. Hoolikamalt vaadeldes näeme, et ainult viie maantee, F, G, H, I ja J sulgemine võib jagada majandusüksuse väiksemateks osadeks. (Tõsi, kui sulgeda korraga mõlemad maanteed A ja B, siis jääb üks linn teistest eraldatuks, aga siis oleme kaks tõkestamist juba ära kasutanud ja tulemuseks on ainult kaks eraldatud üksust nõutud kolme asemel.)
Nüüd proovime sulgeda kõiki kahe maantee kombinatsioone nende viie maantee hulgast ja igal juhul kontrollime kõige väiksema üksuse suurust. Näiteks kui sulgeme maanteed F ja G, siis on kolm tekkivat üksust suurustega 4, 1 ja 7, millest kõige väiksem üksus on suurusega 1.
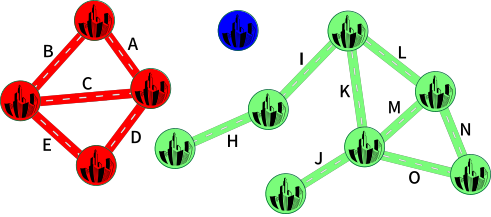
Teised kombinatsioonid, mis toovad kaasa väikese üksuse suurusega 1, on F ja H, F ja J, G ja H, G ja J, H ja I, H ja J ning I ja J, sest maantee H või maantee J sulgemine eraldab alati ühe linna omaette üksuseks.
Maanteede G ja I sulgemine toob kaasa üksused suurustega 5, 2 ja 5, millest kõige väiksema suurus on 2, nagu sellel joonisel:
Järele on jäänud ainult üks kombinatsioon, F ja I. Sel juhul tekivad üksused suurustega 3, 4 ja 5 ning kõige väiksema suurus on 3.
Selles ülesandes soovisime, et kolmest üksusest kõige väiksem sisaldaks võimalikult palju linnu. Seetõttu ongi viimane näide see, mida me otsisime.
Selle ülesande sisuks on sidusate komponentide leidmine suunamata graafis, kus iga kaks tippu on ühendatud vähemalt ühe ahelaga.
Sidusa komponendi leidmiseks võib kasutada graafi läbimist, alustades lähtetipust ja leides süstemaatiliselt teised tipud, mis on lähtetipuga ühendatud, kuni enam uutesse tippudesse liikuda ei saa.
Selles ülesandes tahame lisaks leida sildu. Sild on serv, mille eemaldamisel graafi sidusate komponentide arv suureneb.
Sidusate komponentide analüüsi kasutatakse paljudes arvutinägemise rakendustes huvipakkuvate piirkondade kindlakstegemiseks. Näiteks kasutatakse seda tähtede kujude tuvastamiseks optilises märgituvastuses, esiplaani ja tagaplaani eraldamiseks visuaalses jälgimises ning meditsiiniliste kujutiste töötlemises.

Lemmingute kuningas Hamming tahab saata teate kuningannale, kes elab teises kindluses. Teate kohaletoimetamiseks valib ta välja neli lemmingut ja annab igaühele kas punase või kollase lipu, vastavalt teatele, mida ta tahab saata. Kuid kuningas kardab, et teekonnal võib midagi viltu minna. Seetõttu valib ta välja veel kolm abistajalemmingut ja annab neile lipud järgmiste reeglite alusel.
Teekonnal kuninganna juurde kaotab üks lemming oma lipu. Et oma viga heaks teha, valmistab ta kiiresti uue. Kahjuks ta aga ei mäleta, mis värvi lipp tal alguses oli, seetõttu ei tea ta, kas tema uus lipp on õige või mitte.
Kui lemmingud kuninganna kindlusesse jõudsid, nägi kuninganna järgmist pilti:

Milline järgmistest väidetest on tõene, kui me teame, et täpselt üks lemming kaotas oma lipu ja võis uue lipu teha vale värvi?
[Raadionupud]
A. Uue lipu värv on õige.
B. 1. lemming kaotas lipu ja uue lipu värv on vale.
C. 2. lemming kaotas lipu ja uue lipu värv on vale.
D. 3. lemming kaotas lipu ja uue lipu värv on vale.
E. 4. lemming kaotas lipu ja uue lipu värv on vale.
F. 5. lemming kaotas lipu ja uue lipu värv on vale.
G. 6. lemming kaotas lipu ja uue lipu värv on vale.
H. 7. lemming kaotas lipu ja uue lipu värv on vale.
Õige vastus on D. 3. lemming kaotas lipu ja uue lipu värv on vale.
Nimetame abistajalemmingut koos lemmingutega, keda ta abistab, lemmingute rühmaks ja tähistame seda rühma abistajalemmingu numbriga. Näiteks 5. rühma kuuluvad 5. lemming ja need lemmingud, keda ta abistab, st 1., 2. ja 3. lemming.
Kuninga antud reeglitest abistajatele lippude jagamise kohta võime tähele panna järgmist: enne teekonna algust on igas rühmas punaste lippude arv paaris. Tõepoolest, reeglitest saame, et kui 1., 2. ja 3. lemmingul on kokku paaritu arv punaseid lippe, siis 5. lemmingu lipp on punane, mistõttu punaste lippude koguarv on paaris. Kui aga 1., 2. ja 3. lemmingul on kokku paarisarv punaseid lippe, siis 5. lemminu lipp on kollane, mis jätab punaste lippude koguarvu paarisarvuks. Sama omadus kehtib 6. ja 7. rühmas.
Kontrollime nüüd, kas see omadus kehtib kõigi rühmade puhul pärast lemmingute saabumist kuninganna kindlusesse.

Kõigepealt näeme, et omadus ei kehti kõigi rühmade puhul. See tähendab, et see lemming, kes lipu kaotas, asendas oma lipu vale värvi lipuga, mitte samasugusega, nagu tal enne oli.
Teiseks võime tähele panna, et kui vale värvi lipp on abilisel, siis on omadus rikutud ainult ühes rühmas, nimelt selles, kuhu abiline kuulub. Et meil on omadus rikutud rohkem kui ühes rühmas, siis võime järeldada, et lipu kaotas kas 1., 2., 3. või 4. lemming. Me juba teame, et lemming, kes lipu kaotas, asendas selle vale värvi lipuga. Omadus on rikutud igas rühmas, kuhu see lemming kuulub. Seega peame leidma lemmingu, kes kuulub igasse rühma, kus omadus on rikutud, see tähendab, 5. ja 7. rühma, ja ei kuulu rühma, kus omadus kehtib, see tähendab, 6. rühma. Ainuke selline lemming kannab numbrit 3.
Ülesanne ja abistajalemmingute reeglid on üks näide veaparanduskoodide toimimisest. Üks esimesi veaparanduskoode oli Hammingi kood, mis töötab sarnaste reeglite järgi nagu need, mille andis selles ülesandes kuningas.
Kui me saadame teate, tavaliselt kahendkujul, sidekanalite (juhtmete või raadiolainete) kaudu, siis on keskkonnast pärineva müra tõttu alati võimalus, et teates muutuvad mõned bitid vastupidiseks (muutuvast 0-st 1-ks või vastupidi). Tavaliselt on meie soov kindlaks teha, kas teade on muutunud, ja kui võimalik, siis taastada esialgne teade. Siin ongi abiks veaparanduskoodid.
Üks lihtne viis seda teha on saata teate iga bitti mitu korda. Näiteks kui saadame iga bitti kolm korda, siis saame juhul, kui üks kolmest bitist vastupidiseks muutub, ikkagi leida, mis esialgne bitt oli. Me võime saata iga bitti veelgi rohkem kordi, et kaitsta teadet veelgi suurema arvu bitivigade vastu. Selline lähenemine nõuab aga kolm korda või veelgi rohkem kordi suurema hulga andmete saatmist.
Õnneks võimaldavad mitmed kavalad algoritmid saata üsna vähe lisabitte, lubades samas ikkagi teadet kontrollida ja parandada. Selles ülesandes rakendataksegi ühte sellist meetodit, Hammingi koodi. Hammingi kood tugineb teates olevate bittide rühma summa paarsusele (paarisarvulisusele või paarituarvulisusele), kaasa arvatud lisabitid. Kui kõigis rühmades on paarsused õiged, siis võime eeldada, et teade saabus kohale terviklikul kujul. Kui mõned paarsused on valed, siis muutusid ülekande ajal mõned bitid (mis võivad olla ka lisabitid) vastupidiseks. Kui me teame, et vastupidiseks võib muutuda maksimaalselt üks bitt ja teame ka, milliste rühmade paarsus on vale, siis saame öelda, milline bitt muutus ja mis selle biti algne väärtus oli.
Igal veaparanduskoodil on oma piirangud. Mõned koodid on mõeldud tuvastama ainult seda, et teade muutus, ilma võimaluseta kindlaks teha, milline bitt muutus. Mõned koodid töötavad ainult siis, kui muutus mitte rohkem kui teatud arv bitte. Näiteks selles ülesandes esitatud kood töötab ainult siis, kui maksimaalselt üks lemming asendas oma lipu valega. Kui lipu asendaksid valega kaks lemmingut, siis poleks kuningannal võimalik määrata, millised lipud muutusid. Selles ülesandes me lihtsalt eeldasime, et lipu muutis valeks ülimalt üks lemming. Kui me seda ei teaks, siis võiks juhtuda, et teade saabus kohale vigasena, aga me ei märka seda (näiteks kui 1., 5. ja 6. lemmingu lipud muutusid kõik valeks). Mõistlik on eeldada, et palju bitte vahetub väiksema tõenäosusega kui ainult üks või mõni. Tegelikud sidesüsteemid on tavaliselt siiski keerulisemad ning raskemate juhtudega toimetulemiseks on välja arendatud veelgi keerukamaid koode.
Sarnaseid algoritme saab kasutada ka informatsiooni korrektsuses veendumiseks muudes kohtades, näiteks mitmesuguste kaubakoodide või isikukoodide või pangakontode numbrite juures.

Viis sõpra, Agnes, Benno, Celia, Denis ja Erkki, otsustasid mängida telefonimängu. Agnes sosistab Bennole tähthaaval kümnetähelise sõna (nt K-A-N-A-D-A-L-A-N-E). Seejärel sosistab Benno sõna tähthaaval Celiale, aga teeb ühe vea. Viga võib olla tähe asendamine uue tähega (nt K-A-R-A-D-A-L-A-N-E) või tähe kustutamine (nt K-A-N-A-D-A-L-A-E). Seejärel sosistab Celia sõna tähthaaval Denisile ühe lisaveaga ja nii edasi.
Igal sosistamisel tehakse täpselt üks viga, aga ühe ja sama tähekoha juures võivad sõbrad teha mitu viga.

Kui Agnes sosistab Bennole tähthaaval sõna V-Õ-I-S-T-L-U-S-E-D, siis milliseid järgmistest sõnadest võib Denis sosistada Erkkile?
[Märkeruudud]
A. V-Õ-S-T-E-S
B. V-Õ-Õ-S-T-L-U-S-E-D
C. V-Õ-I-S-T-L-U-S-E
D. V-I-S-T-N-A-S-D
E. Õ-S-T-L-U-S-E
Õige vastus on B, C ja E.
Agnes sosistab Bennole õige sõna. Benno sosistab sõna ühe veaga Celiale. Celia sosistab sõna veel ühe veaga Denisile. Lõpuks sosistab Denis sõna veel ühe veaga Erkkile. Seega hetkeks, mil sõna jõuab Erkkini, on tehtud täpselt kolm viga.
Vastusevariant A on võimatu. Siin on ainult kuus tähte, mis tähendab nelja kustutamist. Meil on aga võimalik maksimaalselt kolm kustutamist.
Vastusevariant B on võimalik. I asendatakse Õ-ga ühe veana. Seejärel asendatakse ükskõik milline täht (näiteks L) teise veana. See täht asendatakse kolmanda veana tagasi esialgse tähega (L). Näiteks V-Õ-I-S-T-L-U-S-E-D → V-Õ-Õ-S-T-L-U-S-E-D → V-Õ-Õ-S-T-M-U-S-E-D → V-Õ-Õ-S-T-L-U-S-E-D.
Vastusevariant C on võimalik. Kustutatakse D. Seejärel asendatakse ükskõik millist tähte kaks korda nii, et esialgne täht tuleb tagasi. Näiteks V-Õ-I-S-T-L-U-S-E-D → V-Õ-I-S-T-L-U-S-E → V-Õ-I-S-T-M-U-S-E → V-Õ-I-S-T-L-U-S-E.
Vastusevariant D on võimatu. Selles sõnas on ainult 8 tähte. See vastab kahele kustutamisele. Peale selle on siin kaks uut tähte (N ja A), mis vastab kahele asendamisele. Seega on siin tehtud rohkem kui 3 viga.
Vastusevariant E on võimalik. Siin on vaja täpset kolm kustutamist (V, I ja D) ning rohkem mitte midagi.
See ülesanne on näide mürast info edastamisel. Müra on selles ülesandes tähtede kustutamine ja asendamine. Me teame, et siin piirdub müra kolme tähega. Seetõttu võime olla kindlad, et Erkkini jõudnud sõna peab sisaldama vähemalt seitset tähte, mis vastavad (järjekorras) esialgsele sõnale.
Tegelikule elule paremini vastav näide infoedastusel tekkivast mürast on bittidest, st numbritest 0 ja 1 koosnevate digitaalsignaalide edastamine. Sellises signaalides võib tekkida samuti asendamise või kustutamise vigu. Asendamine tähendab sellistel juhtudel aga bitivahetust, st 0 asemele tekib 1 ja vastupidi.
Teedrajavat tööd selle kohta, kuidas saata digitaalsignaale edasi peaaegu ilma vigadega, tegi Claude Shannon, tuntud ka kui informatsiooniteooria isa, kes käsitles kanali mõju selle kaudu saadetavale signaalile.

Joostile meeldib valmistada pilte järgmiste sammude abil.

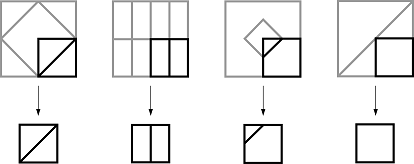
Kui alustada sellistest ruutudest

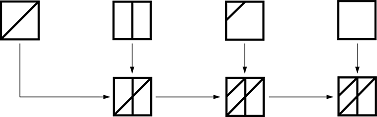
ja kasutada ülal kirjeldatud meetodit, siis milline järgmistest on võimalik pilt pärast neid kolme sammu?
[Raadionupud]
A. 
B. 
C. 
D. 
Õige vastus on C.
Valides ülemise vasaku nurga, saab Joost pildi

Valides ülemise parema nurga, saab Joost pildi

Valides alumise vasaku nurga, saab Joost pildi

Valides alumise parema nurga, saab Joost pildi
Seega pakutud variantidest ainuke, mille Joost võib saada, on variant C, mis tekib alumise vasaku nurga valimisel.
See on ülesanne on näide programmeerimismudeli MapReduce tööst. Seda mudelit kasutatakse suurte andmehulkade töötlemiseks paljude omavahel ühendatud arvutite abil.
Suurtest andmehulkadest eraldatakse informatsioon tegevuse Map abil ja seejärel pannakse kogu see informatsioon kokku tegevuse Reduce abil.
Mudeli on loonud Google, aga seejärel on see muutunud populaarseks ka ettevõttest väljaspool.

Bruno oli koolivaheajal kaks nädalat emal abiks nende kodukohvikus.
Mõlema esmaspäeva hommikul sai ta ema käest 40€ väärtuses münte ja pani need kohviku kassasse vahetusrahaks.
Iga tööpäeva õhtul märkis ta üles kassas oleva raha kogusumma ja sai sellise graafiku:
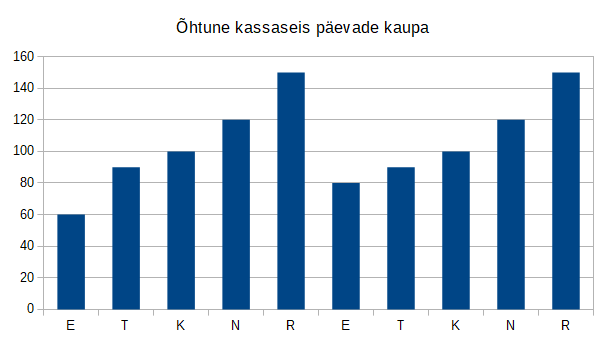
Mõlema reede õhtul võttis ta kassast kogu raha välja ja andis emale.
Mitu eurot oli kohviku suurim päevane sissetulek?
[Tekstikast, täisarv]
Õige vastus on 40€.
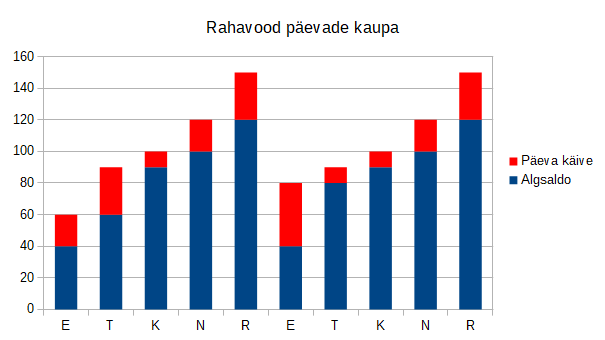
Kohviku käibest parema ülevaate saamiseks toome graafikul välja eraldi kassajäägi hommikul ja õhtul (seejuures on oluline mitte unustada esmaspäeva hommikul algseisuks sisse pandud 40€):
Veel selgem on asi, kui jätame graafikult välja hommikuse jäägi ja keskendume päeval lisandunud summale:
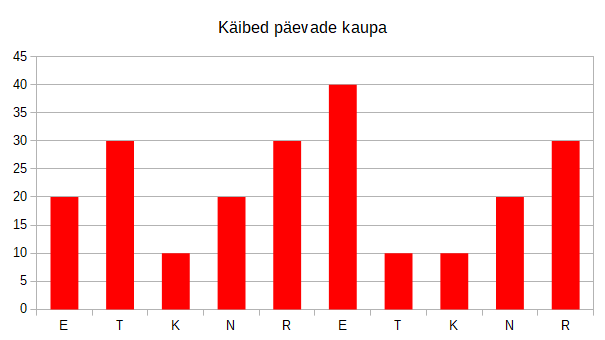
Nüüd on ilmne, et kõige suurema summa, 40€, teenis kohvik teise nädala esmaspäeval.
See ülesanne illustreerib, kuidas andmete esitusviis võib nende põhjal mõnele küsimusele vastamise teha kas lihtsamaks või keerulisemaks. Kui graafiku aluseks olevad andmed on arvutustabelis või andmebaasis, saab esituse parandamiseks vajaliku teisenduse lasta ära teha arvutil. Mida rohkem on andmeid, seda suurem on sellisest automaatsest parandamisest saadav kasu.

Sõnade otsimiseks tekstist võib kasutada regulaaravaldisi (regular expressions). Need võivad sisaldada metamärke, mis määravad keerukamaid otsingureegleid.
Mõned metamärkide näited:
[:space:] – tühikud, näiteks b[:space:]e leiab teksti b e,
? – erisümbol, mis määrab, et selle ees olev märk võib tekstis esineda või puududa, näiteks be?b leiab nii beb kui ka bb.
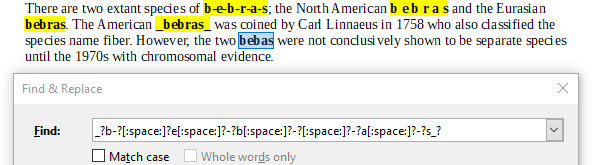
Järgnevas tekstis esineb sõna "bebras" viis korda (paksus kirjas esile toodud), iga kord erinevalt kirjutatuna:
There are two extant species of b-e-b-r-a-s; the North American b e b r a s and the Eurasian bebras. The American bebras was coined by Carl Linnaeus in 1758 who also classified the species name fiber. However, the two bebas were not conclusively shown to be separate species until the 1970s with chromosomal evidence.
Millise regulaaravaldise peaks otsinguaknasse sisestama, et leida tekstist sõna "bebras" kõik viis varianti?
[Raadionupud]
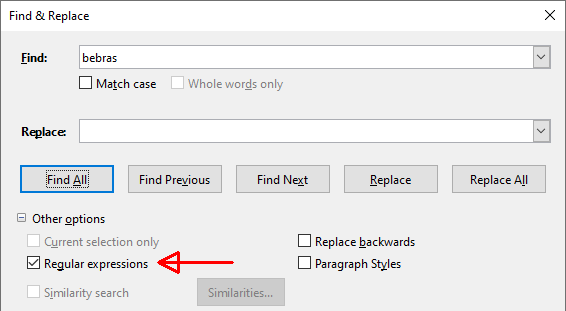
A. _?b-?e-?b-?r?-?a-?s_?
B. _?b-?[:space:]?e[:space:]?-?b[:space:]?-?r?[:space:]?-?a[:space:]?-?s_?
C. _?b[:space:]?e[:space:]?b[:space:]?r?[:space:]?a[:space:]?s_?
D. _?b-?[:space:]?e[:space:]?-?b[:space:]?-?[:space:]?-?a[:space:]?-?s_?
Õige vastus on B. _?b-?[:space:]?e[:space:]?-?b[:space:]?-?r?[:space:]?-?a[:space:]?-?s_?.
Vaatleme iga avaldist eraldi.
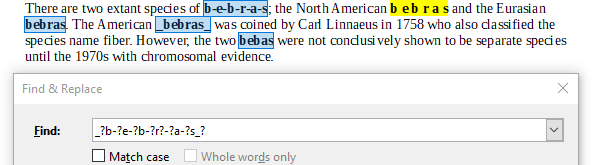
Avaldis A ei leia varianti "b e b r a s", kus tähtede vahel on tühikud:
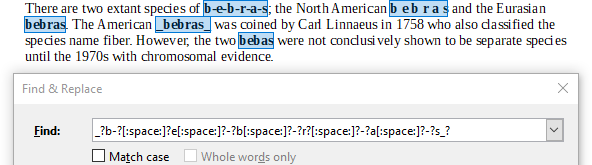
Avaldis B leiab kõik viis varianti:
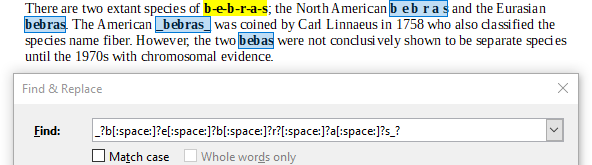
Avaldis C ei leia varianti, kus tähtede vahel on sidekriipsud:
Avaldis D leiab vaid selle variandi, kus täht "r" puudub:
Regulaaravaldisi kasutatakse programmeerimises väga sageli, näiteks osaliselt kokku langevate tekstide, märgihulkade, sõnade otsimisel, tekstiridade valideerimisel, samuti sümbolite või sõnade asendamiel. Neid saab kasutada ka andmete valideermisel, näiteks kui paroolile seatakse minimaalse tähemärkide arvu või suur- ja väiketähtede, numbrite või erimärkide olemasolu nõuded.

Ametlikest turniiridest osavõtmiseks peavad kõik tennisemängijad olema registreeritud riiklikus tenniseassotsiatsioonis. Seepärast peab iga kohalik klubi arvet oma mängijate ja nende registreerimisinfo üle, kasutades tabeleid, kus on read ja veerud. Iga mängija kohta on üks rida. Nende andmete põhjal teeb klubi kindlaks, kas mõnel mängijal on vaja oma registreeringut uuendada.
Milline veergude kombinatsioon on täpselt piisav (st sisaldab küllaldaselt, aga mitte liiga palju andmeid), et teha kindlaks, kas mängijal on vaja uuendada oma registreeringut enne järgmist turniiri (mille toimumise aeg on teada)?
[Raadionupud]
A. Mängija registreerimisnumber, mängija sünnikuupäev, registreeringu lõppemisaeg
B. Mängija registreerimisnumber, registreerimistasu, registreeringu lõppemisaeg
C. Mängija registreerimisnumber, registreeringu viimase uuendamise kuupäev, registreerimisperioodi pikkus
D. Mängija registreerimisnumber, registreeringu viimase uuendamise kuupäev, mängija vanusekategooria
Õige vastus on C.
Registreeringu viimase uuendamise kuupäeva ja registreerimisperioodi pikkuse põhjal saame välja arvutada, millal registreering lõpeb. Mängija registreerimisnumber ütleb meile, millise mängija registreeringut on vaja uuendada.
Valik A ei ole õige, sest meil pole vaja mängija sünnikuupäeva.
Valik B ei ole õige, sest meil pole vaja selles stsenaariumis teada registreerimistasu suurust.
Valik D ei ole õige, sest meil pole vaja selles stsenaariumis teada mängija vanusekategooriat. Lisaks, kui me ei tea registreerimisperioodi pikkust, siis pole registreeringu viimase uuendamise kuupäev üksinda piisav, et tuvastada, millal registreering lõpeb.
Tänapäeva maailma toimimise alus on andmete tabelid, mida nimetatakse andmebaasideks. Informaatikud peavad kavandama nende tabelite struktuuri: milliseid veerge on vaja, millises vormingus, ning kuidas ühe tabeli andmed seostuvad teise tabeli andmetega. Näiteks võib meil olla mängijate isikuandmete tabel, kust saame teada mängija nime, vanuse ja muud detailid iga registreerimisnumbri kohta. Registreerimisnumber on seos isikuandmete rea ja isiku registreerimisandmete vahel.
On kaalumise koht, kui palju andmeid salvestada, ning me peame hoidma selle tasakaalus. Kui me ei kogu piisavalt palju andmeid, siis võib tabel olla kasutu või raskesti töödeldav, kui vastuse kättesaamine olemasolevatest andmetest nõuab liiga palju arvutustööd. Teiselt poolt, kui me kogume liiga palju andmeid "igaks juhuks", siis kuhjame salvestuskoha asjatult andmetega üle, võime tekitada vasturääkivusi (näiteks kui registreeringu viimase uuendamise kuupäev, registreerimisperioodi pikkus ja registreeringu lõppemisaeg ei klapi kokku) või andmete turvalisuse probleeme. Seepärast kasutatakse informaatikas meetodeid (näiteks normaliseerimist), millega määratakse kindlaks tabelite andmete sobiv struktuur.

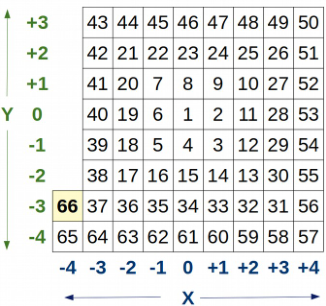
Janil on ruudukujuline märkmik, kuhu ta on hakanud joonistama järjestikuste positiivsete arvude spiraali, alustades ruudust koordinaatidega (0; 0):

Näiteks arvu 19 asukoht on (-2; 0), arvu 27 asukoht on (+3; +1) ning arvu 31 asukoht on (+3; -3).
Kõigi arvude väljakirjutamine muutus talle aga tüütavaks, sest ta tahab tegelikult teada ainult seda, kus asub tema lemmikarv 66. Aita teda!
Millistele koordinaatidele satuks arv 66, kui Jan jätkaks järjestikuste arvude kirjutamist spiraalis?
[Koordinaatide paar (X;Y)]
Õige vastus on (-4; -3).
Seda näeme järgmiselt jooniselt:
Algoritmilise mõtlemise alus on mustrite äratundmine. Praegusel juhul meenutab ruumiline muster spiraali, kõverat, mis lähtub ühest punktist, praegusel juhul asukohast (0; 0), ning liigub ümber algse punkti tiireldes järjest kaugemale. Spiraale esineb tihti looduses, näiteks teokarpide või galaktikate puhul.
Ruumilist asukohta näidatakse sageli koordinaatide abil, nagu siin kasutatud Descartesi koordinaatide süsteem, mis mõõdab punktide horisontaalset ja vertikaalset kaugust algpunktist.

Kõvaketas on salvestusruumi haldamiseks jagatud kindla suurusega klastriteks. Faili salvestamisel võtab see alati enda alla täisarvu klastreid. Kui faili suurus ei jagu klastri suurusega, jääb viimase hõivatud klastri lõpust osa ruumi lihtsalt kasutamata.
Järgneval joonisel on kujutatud 16 KB suurusteks klastriteks jaotatud kõvaketta kasutus, kus juba hõivatud klastrid on hallid ja veel vabad klastrid valged.
Kettale kirjutatakse ükshaavad järgmised failid: kõigepealt fail A suurusega 20 KB, siis fail B suurusega 18 KB, siis fail C suurusega 34 KB ning lõpuks fail D suurusega 48 KB. Operatsioonisüsteem püüab leida failide salvestamiseks järjestikused vabad klastrid, et vältida failide fragmenteerumist, st faili tükeldamist erinevate kettaosade vahel, mis vähendab arvuti jõudlust.
Üks lähenemine failide fragmenteerumist vähendada on selline.
Otsida esimene järjestikuste vabade klastrite kogum, kuhu mahub terve fail.
Kui sellist kogumit pole, siis tükeldada fail nii, et saadavad tükid saab paigutada esimestesse vabadesse klastritesse.
Milline näeb failisüsteem välja pärast seda, kui eelkirjeldatud reeglite järgi kirjutatakse sinna failid A (punane), B (roheline), C (sinine) ja D (kollane)?
[Raadionupud]
A. 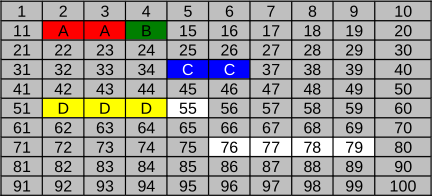
B. 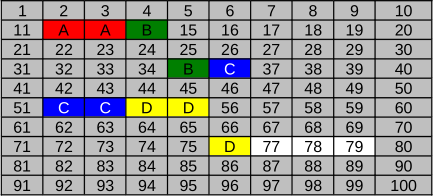
C. 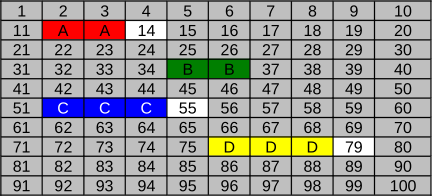
D. 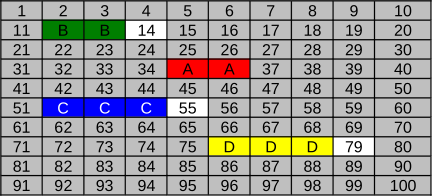
Õige vastus on C.
Fail A (20 KB) kirjutatakse klastritesse 12 ja 13 (vaba ruumi 32 KB jaoks).
Fail B (18 KB) kirjutatakse klastritesse 35 ja 36 (vaba ruumi 32 KB jaoks). Klaster 14 jääb kasutamata, sest selle kasutamine põhjustaks faili B fragmenteerimise, mida saab vältida klastrite 35 ja 36 kasutamisega.
Fail C (34 KB) kirjutatakse klastritesse 52, 53 ja 54 (vaba ruumi 48 KB jaoks).
Fail D (48 KB) kirjutatakse klastritesse 76, 77 ja 78 (vaba ruumi 48 KB jaoks).

Variant A ei ole õige vastus, sest selle kohaselt hõivab fail B ainult ühe klastri. Kuna klastri suurus on 16 KB, et saa 18 KB suurune fail ühte klastrisse mahtuda. Samamoodi ei saa ka fail C mahtuda kahte klastrisse.
Variant B ei ole õige vastus, sest selle kohaselt fail B salvestamisel fragmenteeriti, aga 1. reegli kohaselt seda ei tehta, kui leidub piisava suurusega järjestikuste vabade klastrite hulk. Samamoodi fragmenteeriti asjatult ka failid C ja D.
Variant D ei ole õige vastus, sest selle kohaselt salvestati fail A klastritesse 35 ja 36, kuigi faili A salvestamise ajal olid vabad ka klastrid 12 ja 13 ning reegli 1 kohaselt oleks pidanud faili A salvestama esimesse piisava suurusega vabasse alasse.
See ülesanne näitab, kuidas kõvakettal informatsiooni hoitakse ja selgitab failide fragmenteerumise mõistet.
Ülesande näites kannatab failisüsteemi algseis juba välise fragmenteerumise all, mille tagajärjel on vabade järjestikuste klastrite kogumid kettal väikesed. Väline fragmenteerumine tekib, kui luuakse, muudetakse või kustutatakse erinevate suurustega faile.
Kui luuakse suur fail ja kettal pole selle salvestamiseks piisavalt suurt järjestikuste vabade klastrite kogumit, siis tükeldatakse fail väiksemateks osadeks ja kirjutatakse need failisüsteemi. Seda protsessi nimetatakse faili fragmenteerimiseks. Selle puuduseks on kõvaketta jõudluse vähenemine.
Kolmas fragmenteerumise liik esineb arvuti operatiivmälu (RAM) halduses. Ka operatiivmälu on jaotatud kindla suurusega lehekülgedeks ja selle jagamine programmide vahel toimub lehekülgede kaupa. Tavaliselt kasutab programm mitut lehekülge, kusjuures tihti ei saa viimane lehekülg täielikult täidetud ning mälusse jääb vaba ruum, mida teised programmid enam kasutada ei saa. Seda nimetatakse sisemiseks fragmenteerumiseks.
Copyright © 2020 Bebras – International Challenge on Informatics and Computational Thinking.
Licensed under Creative Commons Attribution-ShareAlike 4.0 International License.
Flag icons by GoSquared.