

Доктор Бор знает, что один из его 16 пациентов заражён. Однако у него имеется только 8 пробирок: A, B, C, D, E, F, G и H. Чтобы найти заражённого пациента, ему надо получить пробу крови, где будет присутствовать заражение. У каждого бобра он берёт пробу, и часть проб он смешивает в обозначенных пробирках с пробами других бобров. Он внимательно следует плану распределения пробирок:
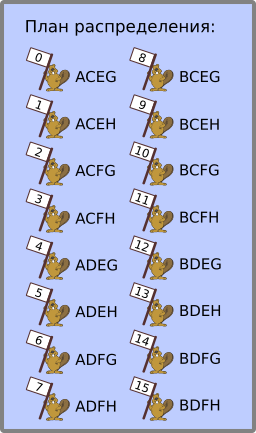
Например, проба крови бобра под номером 0 распределяется между пробирками A, C, E и G:
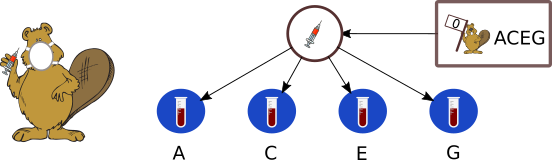
На данный момент доктор Бор уже проверил пробирки A (заражена), C (здоровая) и E (здоровая).

Какую из этих 4 пробирок должен доктор Бор проверить следующей, чтобы найти заражённого бобра?
[Raadionupud]
Пробирка B
Пробирка D
Пробирка F
Пробирка G
Правильный ответ 4. Пробирка G.
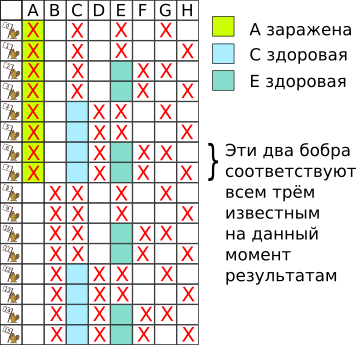
На основании уже проведённых тестов заражённым будет 6-ой или 7-ой бобр. В пробирке G имеется проба крови 6-ого бобра, но нет крови 7-ого бобра; в пробирке H, наоборот, имеется проба крови 7-ого бобра, но нет крови 6-ого бобра. Так как нам известно, что заражён только один бобр, то проверка пробирки G или H (мы узнаем, является ли она заражённой или здоровой) позволит определить, кто же из этих двух бобров заражён. Таким образом, из предложенных вариантов правильным ответом будет пробирка G.
Результаты проверок пробирок B, D и F не зависят от того, является 6-ой или 7-ой бобр заражённым (в любом случае в пробирке В содержится только здоровая кровь; в пробирках D и F в обоих случаях содержится заражённая кровь). Таким образом, проверка этих пробирок не помогла бы доктору Бору.
Групповое тестирование - это техника, которую Ричард Дорфман придумал во время второй мировой войны для проверки проб крови. Начиная с этого времени, эта техника применяется не только в биологии, но и в других областях, например, в технике и информатике, особенно с целью обнаружить повреждения.
Для проведения группового тестирования имеются различные алгоритмы. Какой из них будет самым лучшим, зависит от особенности решаемой проблемы. Для читателя, который знаком с двоичным поиском, хорошим пунктом отправления будет обобщённый алгоритм двоичного расщепления.
Приведённый в начале задания план распределение пробирок на самом деле основывается на двоичном представлении номеров бобров (0=0000_2, 1=0001_2, ..., 15=1111_2), где A, C, E, G являются все 0, а B, D, F, H - все 1.

На завод по изготовлению качелей пришла новая партия брёвен, все длиннее 1 м.
Завод хочет изготовить вот такие качели:

Важно - сиденье качели должно быть вот таким:
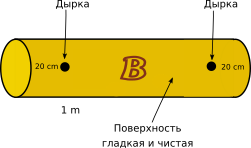
На заводе имеется четыре робота, которые могут работать параллельно:
Резак отрезает от бревна один конец таким образом, что остаётся бревно длиной ровно 1 м.
Кородёр удаляет с бревна кору и делает поверхность гладкой и чистой.
Дрель сверлит в бревне дырки на расстоянии точно 20 см от левого конца и точно 20 см от правого конца.
Принтер печатает точно по центру гладкого и чистого бревна логотип завода.
Один робот одновременно обрабатывает только одно бревно, и на обработку одного единственного бревна у роботу уходит ровно одна минута. Робот должен работать с бревном один, то есть в это же самое время какой-нибудь другой робот не может работать с этим же бревном. Когда все брёвна обработаны, то робот останавливается.
Робот приступает к работе после того, как получит сигнал к началу работы от программы управления. Робота нельзя включить, если нет пригодных для обработки брёвен. Команды программы управления запускаются одна за другой.
Имеется 4 созданных программы управления. Согласно одной из них, каждый робот работает только с брёвнами и столько времени, сколько потребуется. Какая это программа?
[Raadionupud]
A. 
B. 
C. 
D. 
Правильный ответ A.
Прежде всего, резак и кородёр работают в одно и то же время, а дрель и принтер приступают к работе только после того, как два первых робота закончат свою работу. Это всё потому, что они нуждаются в брёвнах длиной 1 метр. К тому же принтер работает только гладкими и чистыми брёвнами.
Команды запуска, которые располагаются перед командой ожидания, можно поменять между собой местами, и это не повлияет на работу программы. Также можно поменять между собой и команды запуска, которые располагаются после команды ожидания.
В варианте ответа B принтер работает перед кородёром. В варианте ответа C принтер работает перед резаком и поэтому не "знает", где находится центр качели. В варианте ответа D принтер и кородёр работают одновременно, а это значит, что некоторые брёвна сначала обрабатывает принтер.
Данное задание иллюстрирует две основные техники параллельных вычислений: 1) преобразование и 2) синхронизация процессов.
Преобразование - это альтернатива итерации. Определим функцию и с её помощью преобразуем множество объектов. Это значит, что мы применим эту функцию к каждому элементу этого множества, причем неважно в каком порядке. Так как функцию можно выполнить параллельно на нескольких процессорах, то преобразование будет быстрее итерации. Пример на Python:
>>> puuviljad = ['pirn', 'apelsin', 'kirss']
>>> s = map(str.upper, puuviljad)
>>> print(list(s))
['PIRN', 'APELSIN', 'KIRSS']Здесь последовательность строк преобразуется с помощью строкового метода upper().
Роботы из данного задания могут работать с брёвнами параллельно. Программа управления следит, чтобы дрель и принтер не начали работать пока резак и кородёр не закончат свою работу. Это называется синхронизацией процессов. Во время работы за компьютером надо также следить, чтобы работающие с одними и теми же данными программы не мешали друг другу.

Группа бобров хочет прогреть свои холодные дома с помощью отопительных элементов. Их дома состоят из множествa камер.
Отопительный элемент занимает одну камеру и способен сразу её прогреть. В течение 1 минуты тёплый воздух проникает из прогретой камеры во все расположенные рядом камеры (это камеры, у которых с прогретой камерой имеется общий угол и/или стена).

На вышеприведённом рисунке показано, сколько минут понадобится для прогревания каждой камеры маленького дома, если отопительный элемент расположен в отмеченным синим цветом камере.
Помоги бобрам расположить 4 отопительных элемента в большом доме, который изображён на нижеприведённом рисунке, так, чтобы дом прогрелся как можно быстрее.
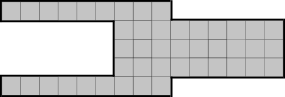
Сколько времени понадобится, чтобы прогреть весь большой дом?
[Raadionupud]
A. 1 минута
B. 2 минуты
C. 3 минуты
D. 4 минуты
Правильный ответ B. 2 минуты.
Если отопительные элементы расположены так, как показано на рисунке, то для прогрева всех камер понадобится 2 минуты.
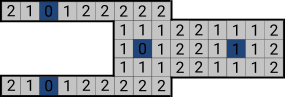
За 1 минуту невозможно прогреть все камеры. На самом деле, чтобы прогреть весь дом за одну минуту, все камеры должны находиться в непосредственной близости к отопительным элементам. В доме имеется 36 камер, а это значит, что каждый отопительный элемент должен быть соединён с 9 различными камерами (включая ту, где находится сам элемент). Учитывая форму дома, такое, к сожалению, невозможно. Есть другая возможность: заметим, что в доме есть цепочки из 15 располагающихся последовательно камер. Так как каждый отопительный элемент может "покрыть" цепочку, состоящую максимально из 3 камер, то 4 элемента не смогут "покрыть" такую цепочку. Поэтому наименьшим временем будет 2 минуты, то есть ответ B.
Это задание связано с распространением информации в графе, который выступает здесь как модель дома. Каждая камера представляет одну вершину. Две вершины соединены ребром, если соответствующие камеры являются соседними, как указано в условиях задания. В данном задании мы должны выбрать вершины (камеры), откуда доберёмся (тёплый воздух) до всех вершин графа (камеры), используя при этом наименьшее количество рёбер (соседних камер).

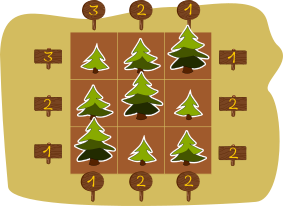
Бобры высаживают в парке девять деревьев таким образом, что они образуют три ряда, в каждом по три дерева. Имеются деревья разной высоты:  ,
,  и
и  . В каждом ряду и каждом столбце имеется ровно по одному дереву каждой высоты (то есть ни в одном ряду и ни в одном столбце нет двух деревьев одинаковой высоты).
. В каждом ряду и каждом столбце имеется ровно по одному дереву каждой высоты (то есть ни в одном ряду и ни в одном столбце нет двух деревьев одинаковой высоты).
С каждой стороны парка (смотри нижеприведённый рисунок) бобры смотрят, сколько же деревьев просматриваются с этой точки обзора, и записывают это число на знаке (знак  обозначает столбцы, а знак
обозначает столбцы, а знак  ряды):
ряды):

Бобр, смотрящий на растущие на одной линии деревья, не видит те деревья, которые находятся за более высокими деревьями:

Если числа будут такими, как приведены на рисунке ниже, то какой из предложенных вариантов подходит для самого нижнего ряда (слева направо)?
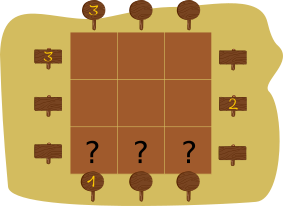
[Raadionupud]
A. 


B. 


C. 


D. 


Правильный ответ B.
Положения двух "троек" будет достаточным, чтобы точно восстановить весь парк.
Если с какой-то точки обзора видны все деревья, значит, смотря с этой точки, деревья упорядочены по высоте, начиная с самого низкого  ,
,  ,
,  . Значит, мы можем уже расположить деревья в первом ряду и первом столбце:
. Значит, мы можем уже расположить деревья в первом ряду и первом столбце:
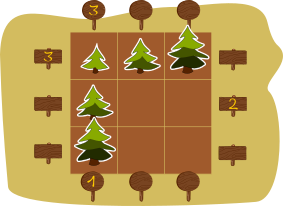
Так как в каждом ряду и в каждом столбце может быть ровно по одному дереву каждой высоты, то в среднем квадрате нижнего ряда должно быть  , так как в среднем столбце уже есть
, так как в среднем столбце уже есть  , а в нижнем ряду уже есть
, а в нижнем ряду уже есть  . А затем в правом нижнем углу должно быть
. А затем в правом нижнем углу должно быть  , так как деревья
, так как деревья  и
и  уже есть в нижнем ряду.
уже есть в нижнем ряду.
На самом деле и для расположения оставшихся деревьев имеется только одна возможность:
Данное задание требует два основных навыка информатики. Первый навык - это умение находить решение, которое удовлетворяет условиям задачи. Второй навык - это умение восстановить объект, основываясь на частичной информации, используя знания о свойствах названных объектов. Это можно использовать при сжатии представления объекта. В информатики этот процесс описывается как сжатие без потерь, так как при восстановлении информация не теряется.

Часть Бобруйска состоит из определённого количества островов, соединённых между собой мостами. Для каждого моста действует ограничение по грузоподъёмности, и транспортное средство, которое превышает это ограничение, не может проехать по мосту. Общая масса транспортного средства является суммой веса самого транспортного средства и перевозимого на нём груза.
Ниже приведена карта островов Бобруйска, где острова представлены в форме кружков, а мосты в форме отрезков. Рядом с каждым мостом указано действующее ограничение по грузоподъёмности.

"Поставки из Бобруйска" - это фирма по доставке грузов, где используются грузовики массой 10 тонн с максимальным подъёмным весом перевозимого груза 30 тонн.
Какое наименьшее количество рейсов должен совершить один единственный грузовик, чтобы доставить 250 тонн песка с острова А на остров В?
[Raadionupud]
A. 10
B. 11
C. 12
D. 13
Правильный ответ C.
Вычислим ответ в два этапа. На первом этапе найдём, какова максимальная масса груза, которую грузовик сможет за один раз перевезти с острова А на остров В (допустим, что это масса x). На втором этапе вычислим, сколько поездок должен грузовик сделать с острова А на остров В, чтобы перевезти весь песок.
Для нахождения значения x вычислим наибольшую общую массу, которую за один раз можно перевезти с острова А на другой остров. Общая масса состоит из веса грузовика и веса груза. Очевидно, что наибольшая общая масса, которую можно будет доставить на остров А, будет 10 т + 30 т = 40 т. Применим жадный подход, то есть по возможности постараемся доставить на следующий остров наибольшую общую массу. У нас складывается следующая ситуация:
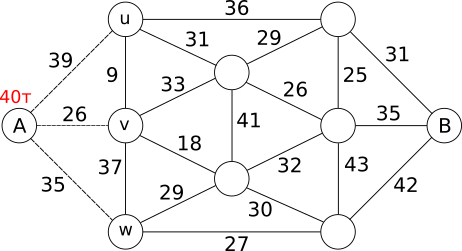
На острове А у нас имеется 40 т, которые мы можем по обозначенным пунктиром мостам доставить на острова u, v и w. Жадный подход предполагает доставку наибольшей общей массы через мост с наибольшей грузоподъёмностью, то есть по мосту к острову u. Однако из-за ограничений по грузоподъёмности моста мы сможем доставить только 39 т. Теперь у нас следующая ситуация:
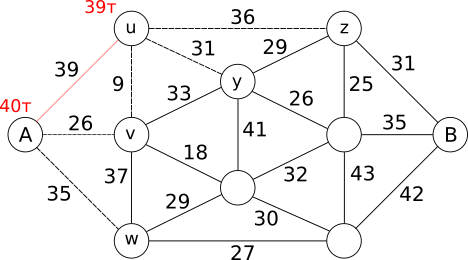
которая подсказывает нам, что наибольшей общей массой, которую за один раз мы можем вывезти с острова А, будет 39 т. Теперь посмотрим, куда дальше мы должны доставить эту массу. С острова u к рассматриваемым островам w, v, y и z опять ведут обозначенные пунктиром мосты. С острова А на остров v мы можем доставить 26 т, а на остров w - 35 т. Однако с острова u на остров y мы можем доставить 31 т, а на остров z - 36 т. Так как мы по-прежнему жадные, то доставим 36 т на остров z, и у нас сложится следующая ситуация:
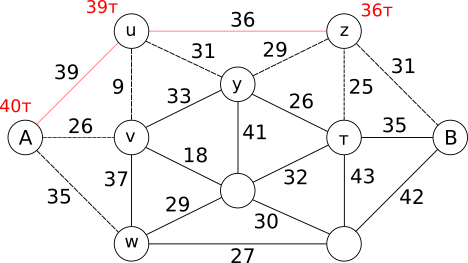
Теперь мы знаем, что наибольшую общую массу, которую за один раз мы сможем доставить на остров А, будет 40 т (очевидно), на остров u - 39 т и на остров z - 36 т. В данной ситуации мы можем доставить, опять-таки обращая внимание на обозначенные пунктиром мосты, на остров w - 35 т с острова А, на остров v - 26 т также с острова A, на остров y - 31 т с острова u, на остров t - 25 т с острова z и на остров B - 31 т также с острова z. Хотя мы могли бы выбрать остров B, но мы продолжим применять свою жадную философию и используем остров w.
Здесь мы не будем описывать все шаги решения, просто изобразим итоговую ситуацию:
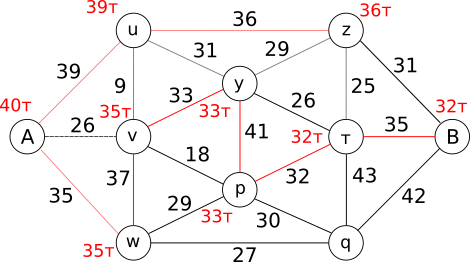
На рисунке показано, какая наибольшая общая масса может быть доставлена за один раз с острова А на каждый другой остров, какие мосты мы при этом должны проезжать. Рядом с островом q не указана наибольшая общая масса, но нам и не надо её вычислять, потому что мы уже добрались до острова B. В итоге мы получили, что наибольшая общая масса, которую можно за один раз доставить с острова А на остров В, будет 32 т, и мы проедем по островам w, v, y, p и t. Таким образом, доставляемый груз должен весить максимально 22 т, так как 10 т - это вес грузовика. Мы завершили первый этап решения и получили, что максимальный груз, который грузовик доставит с острова А на остров B, будет x = 22 т.
В начале второго этапа вспомним, что надо доставить 250 т песка. За 10 поездок грузовик перевезёт 220 т, за одиннадцатую - 242 т. Нам надо будет совершить ещё одну, двенадцатую по счёту, поездку с 8 т. Итак, мы получили 12 поездок.
Те, кто знаком с функцией потолка целой части (⌈⌉), могут записать решение вычислений в виде ⌈250 т / 22 т⌉ = ⌈11,36...⌉ = 12.
Данное задание является примером задачи о самом широком пути из теории графов. Она применяется, например, при нахождении максимальной пропускной способности сети между заданными пунктами и в других задачах на тему "бутылочного горлышка". Также её можно рассматривать как подчасть в задании на нахождение максимальной пропускной способности, которое используется в алгоритме Форда-Фалкерсона для нахождения максимального потока.
Если немного дополнить наш жадный алгоритм, то, по сути, мы получим алгоритм Прима для нахождения минимального остовного дерева. Основное дополнение связано с количеством рассматриваемых за один шаг пунктирных мостов. Например, обратившись ко второй ситуации, когда мы узнали о том, что на остров u может быть доставлено 39 т общей массы, мы рассматривали два моста до острова v: с острова A и с острова u. Эту избыточность можно избежать, если используем структуру данных, которая называется порядок предпочтений, и сохраняем в ней только лучший выбор из двух имеющихся.

В распоряжении Карины имеется 5 бытовых приборов: компьютер, стиральная машина, телевизор, кофеварка и пылесос. Для управления этими машинами используется 5 кнопок A, B, C, D и E.
Однако работа кнопок реализована не самым удачным образом. Так как кнопки соединены с несколькими приборами, то каждая кнопка одновременно включает или выключает несколько приборов. А именно нажатие на кнопку меняет состояние всех приборов, соединённых с этой кнопкой, на противоположное: то, что было раньше выключёно, теперь включено; то, что было раньше включено, теперь выключено.
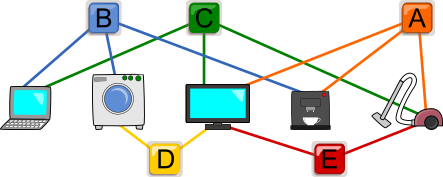
Какая последовательность кнопок будет правильной, чтобы включить только телевизор и кофеварку?
[Raadionupud]
Правильный ответ 4. B, D, C, E.
Если нажать на кнопку B, то включаются компьютер, стиральная машина и кофеварка.

Далее, нажав на кнопку D, выключим стиральную машину, но включим телевизор.

Затем, нажав на кнопку C, выключим компьютер и телевизор, но включим пылесос.

В конце, нажав на кнопку E, включим телевизор, но выключим пылесос.

Теперь у нас включены телевизор и кофеварка, а все остальные приборы выключены.
Чтобы понять, что этот вариант будет правильным, а все остальные - неправильными, достаточно рассмотреть каждую кнопку и прибор по отдельности. Видим, что если кнопку нажимают нечётное количество раз, то в конце концов соединённые с этой кнопкой приборы оказываются включёнными. Если же кнопку нажимают чётное количество раз, то приборы остаются выключенными. То же самое действует и в отношении отдельных приборов: если соединённых с прибором кнопок нажимать нечётное количество раз, то прибор включится, в случае чётного количества нажатий прибор останется выключённым.
Это позволяет нам провести следующий анализ.
В случае первой последовательности (E, C, B, A) мы видим, например, что пылесос соединён с тремя нажимаемыми кнопками (E, C, A). Поэтому пылесос останется включённым, а это не то, что нам надо.
В случае второй последовательности (C, B, A, D) мы видим, что кофеварка соединена только с двумя нажимаемыми кнопками (B, A). Таким образом, она останется выключенной, а это опять нас не устраивает.
Наконец, в случае третьей последовательности (D, A, E, C) мы видим, что, например, стиральная машина соединена только с одной нажимаемой кнопкой (D). Это означает, что она останется включённой, а это нам не подходит. Точнее, включёнными останутся все приборы кроме телевизора.
Аналогичный подход действует и в отношении правильного варианта ответа (B, D, C, E), где кнопки нажимают следующее количество раз.
Приведённые в этом задании приборы мы можем представить в виде чисел, которые увеличиваются каждый раз после нажатия на соединённую с ними кнопку. Правда в нашем случае, счёт числа идёт только до одного, после чего оно вновь начинается с нуля.
Мы имеем дело с используемой в компьютерах двоичной системой. В компьютере вся информация хранится и обрабатывается только с помощью двух чисел - 0 и 1. Например, при выполнении действия сложения за один раз компьютер складывает числа одного разряда и каждый раз, когда результат превышает 1, переносит остаток в старший разряд. Этот процесс демонстрирует приведённая таблица:
| A = 0 1 | A = 0 0 | A = 0 1 |
| B = 0 1 | B = 1 1 | B = 1 0 |
| A + B = 1 0 | A + B = 1 1 | A + B = 1 1 |
В рамках данного задания нас интересует только сложение чисел (перенос мы проигнорируем), причём числа будут описывать состояние приборов (1 = включён, 0 = выключен). Таким образом, при каждом нажатии на кнопку прибавляем к состоянию прибора (0 или 1) единицу:
0 + 1 = 1
1 + 1 = 0

В долине бобров находится 12 городов, соединённые между собой шоссе (обозначены буквами от A до O), как показано на карте:
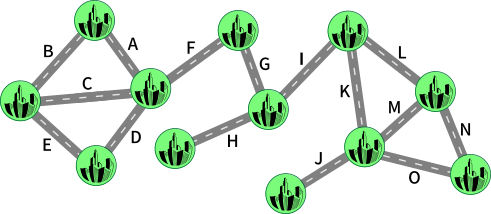
Города, которые соединены между собой с помощью прямого или косвенного шоссе, образуют экономическую зону. На данный момент все 12 городов входят в одну и ту же экономическую зону.
Из-за вспышки эпидемии мэры городов решили закрыть два шоссе, чтобы уменьшить количество поездок между городами. Цель принятого решения в том, чтобы поделить всю долину на три отдельных экономических зоны. Чтобы уменьшить экономический разрыв, в самую маленькую из этих трёх экономических зон должны входить по возможности много городов.
Какие два шоссе необходимо закрыть?
[Tekstikast, 2 tähte]
Правильный ответ F и I.
Некоторые шоссе можно проигнорировать, потому что их закрытие не поделит экономическую зону. Например, если перекрыть шоссе C, то жители всё равно смогут ездить по шоссе A и B. Если мы внимательно присмотримся, то заметим, что перекрытие только пяти шоссе (F, G, H, I и J) может разделить экономическую зону на маленькие части. (Правда, если одновременно перекрыть оба шоссе А и В, то один город останется изолированным от других городов. Но в таком случае мы уже установим две преграды, а в результате у нас будет только две изолированные зоны вместо требуемых трёх.)
Теперь попробуем перекрыть все комбинации из двух шоссе, которые найдутся в состоящем из пяти шоссе множестве. При этом мы каждый раз будем проверять размер самой маленькой зоны. Например, если мы перекроем шоссе F и G, то три возникшие зоны будут размером 4, 1 и 7, из которых наименьшая зона будет размером 1.
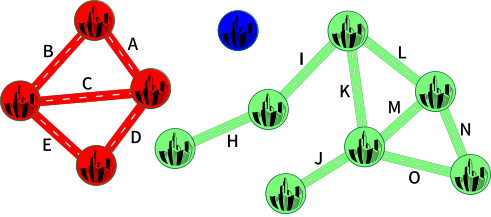
Другие комбинации, которые приведут к появлению маленькой зоны размером 1, будут F и H, F и J, G и H, G и J, H и I, H и J, а также I и J, так как перекрытие шоссе H или J всегда приводит к образованию состоящей из одного города зоны.
Перекрытие шоссе G и I приведёт к возникновению зон размером 5, 2 и 5, из которых наименьшая зона будет размером 2, как и показано на рисунке:
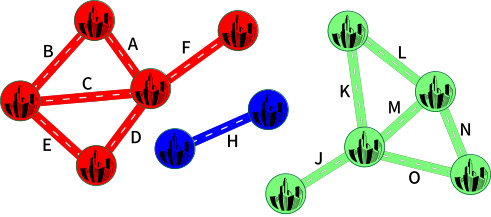
Осталась только одна комбинация - F и I. В этом случае появятся зоны размером 3, 4 и 5, из которых наименьшая зона будет размером 3.
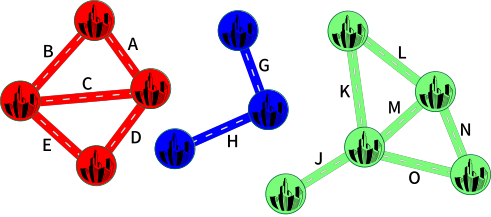
В этом задании мы хотели, чтобы в самую маленькую из этих трёх экономических зон входило по возможности много городов. Таким образом, последний пример и будет искомым решением.
Суть этого задания заключается в поиске связных компонент в неориентированный графе, в котором каждые две вершины соединены между собой по меньшей мере одной дугой.
Для поиска связного компонента можно воспользоваться обходом графа. Мы начнём с начальной вершины и с помощью систематичного подхода будем находить другие вершины, которые соединены с начальной вершиной. Мы будем это делать до тех пор, пока больше не останется возможности перемещаться к новым вершинам.
В этом задании мы также хотим найти мосты. Мост - это ребро, удалив которое число связных компонентов графа увеличится.
Анализ связных компонентов используется во многих приложениях компьютерного "зрения" для определения интересующих нас областей. Например, это используется для определения форм звёзд в процессе их оптического распознавания, для разделения переднего и заднего планов при визуальном наблюдении, а также при обработке медицинских снимков.

Король леммингов Хэмминг решил отправить живущей в другом замке королеве сообщение. Для доставки сообщения он выбрал четырёх основных леммингов, и, в зависимости от отправляемого сообщения, дал каждому из них красный или жёлтый флаг. Однако король боялся, что по дороге может что-то случиться. Поэтому он выбрал ещё трёх помощников леммингов и раздал им флаги в соответствии со следующими правилами.
5-ый лемминг помогает 1-ому, 2-ому и 3-ему леммингам: если количество красных флагов у всех этих основных леммингов было нечётным, то 5-ый лемминг получил красный флаг, в противном случае - жёлтый.
6-ой лемминг помогает 1-ому, 2-ому и 4-ому леммингам: если количество красных флагов у всех этих основных леммингов было нечётным, то 6-ой лемминг получил красный флаг, в противном случае - жёлтый.
7-ой лемминг помогает 2-ому, 3-ему и 4-ому леммингам: если количество красных флагов у всех этих основных леммингов было нечётным, то 7-ой лемминг получил красный флаг, в противном случае - жёлтый.
По пути к королеве один лемминг потерял свой флаг. Чтобы исправить свою ошибку, он быстро смастерил новый. К сожалению, он не помнил, какого цвета был его первоначальный флаг. Поэтому он не знает, является ли новый флаг правильным или нет.
Когда лемминги прибыли к замку королевы, то она увидела следующую картину:

Какое из приведённых утверждений будет верным, если мы знаем, что точно один лемминг потерял флаг и мог для создания нового флага использовать неправильный цвет?
[Raadionupud]
A. Цвет нового флага правильный.
B. 1-ый лемминг потерял флаг, и цвет нового флага неправильный.
C. 2-ой лемминг потерял флаг, и цвет нового флага неправильный.
D. 3-ий лемминг потерял флаг, и цвет нового флага неправильный.
E. 4-ый лемминг потерял флаг, и цвет нового флага неправильный.
F. 5-ый лемминг потерял флаг, и цвет нового флага неправильный.
G. 6-ой лемминг потерял флаг, и цвет нового флага неправильный.
H. 7-ой лемминг потерял флаг, и цвет нового флага неправильный.
Правильный ответ D. 3-ий лемминг потерял флаг, и цвет нового флага неправильный.
Назовём помощника и основных леммингов, которым он помогает, группой леммингов. Обозначим эту группу тем же номером, что и помощника леммингов. Например, в группу №5 входят 5-ый лемминг и те основные лемминги, которым он помогает, то есть 1-ый, 2-ой и 3-ий лемминги.
Обратим внимание на правило, которому следовал король, когда раздавал помощникам флаги: до начала пути количество красных флагов в каждой группе было чётным. Действительно, основываясь на правилах, мы получим, что, если количество красных флагов у 1-ого, 2-ого и 3-его основных леммингов будет нечётным, то 5-ый лемминг получит красный флаг. А это значит, что количество красных флагов станет чётным. Если же количество красных флагов у 1-ого, 2-ого и 3-его основных леммингов будет чётным, то 5-ый лемминг получит жёлтый флаг. А это уже значит, что количество красных флагов станет нечётным. Аналогичная ситуация будет в группах №6 и №7.
Проверим, сохранится ли эта ситуация во всех группах к моменту, когда лемминги прибудут к замку королевы.

Сразу заметим, что такая ситуация сохранилась не во всех группах. Это означает, что потерявший флаг лемминг смастерил новый флаг с неправильным цветом (не тем, что у него был первоначально).
Также можем заметить, что, если флаг неправильного цвета будет у помощника, то ситуация будет нарушена только в одной группе, а именно в той, в которую входит помощник. Так как изменения произошли больше чем в одной группе, то сделаем вывод: флаг потерял 1-ый, 2-ой, 3-ий или 4-ый лемминг. Мы уже отметили для себя, что потерявший флаг лемминг заменил его на флаг неправильного цвета. Ситуация изменилась во всех группах, куда входил этот лемминг. Таким образом, мы должны найти лемминга, который входит в каждую группу, где произошли изменения (в группе №6 ситуация не изменилась). Этими группами могут быть группы №5 и №7. Единственным таким леммингом является лемминг под номером 3.
Задание и правила для помощников леммингов являются примером работы корректирующих кодов. Одним из первых корректирующих кодов был код Хэмминга, который работает по правилам, использованным королём в данном задании.
Если мы отправляем сообщение (обычно в двоичном виде) через каналы связи (по проводам или радиоволнам), то из-за возникающих в окружающей среде помех всегда есть вероятность того, что некоторые биты в сообщении изменятся на противоположные (0 изменится на 1 или наоборот). Разумеется, у нас есть желание узнать, изменилось ли сообщение и, по возможности, восстановить его в первоначальном виде. В таких ситуациях нам и помогают корректирующие коды.
Одна из простых возможностей - это посылать каждый бит сообщения несколько раз. Например, если мы пошлём каждый бит три раза, то в случае, если один из трёх битов изменится на противоположный, у нас всё-таки будет возможность узнать, каким был первоначальный бит. Мы можем каждый бит посылать ещё большее количество раз, чтобы защитить сообщение от ещё большего количества ошибочных битов. Однако такой подход требует посылки в три (а то и больше) раза большего объёма данных.
К счастью, некоторые хитрые алгоритмы позволяют посылать довольно малое количество дополнительных битов, но при этом у нас остаётся возможность проверить и исправить сообщение. В данном задании и показано применение одного из таких методов - кода Хэмминга. Код Хэмминга основывается на чётности (чётное или нечётное число) суммы группы имеющихся битов, включая дополнительные биты. Если во всех группах чётность верна, то можем предположить, что сообщение было доставлено в целостности. Если некоторые чётности неверны, то во время передачи некоторые биты (а это могут быть и дополнительные биты тоже) изменились на противоположные. Если мы знаем, что противоположным может стать максимально один бит, и знаем также, в какой группе имеется неверная чётность, то можем сказать, какой же бит изменился, и какое первоначальное значение было у этого бита.
У каждого корректирующего кода есть свои ограничения. Некоторые коды позволяют определять только сам факт того, что сообщение изменилось, но не позволяют определять какой именно бит изменился. Некоторые коды работают только тогда, когда изменилось не более чем определённое количество битов. Например, представленный в этом задании код работает только тогда, когда максимально один лемминг заменяет свой флаг на неправильный. Если бы два лемминга заменили свои флаги на неправильные, то у королевы не было бы шансов узнать, какие же флаги были заменены. В данном задании мы просто предположили, что флаг заменил исключительно один лемминг. Если бы мы этого не знали, то могло случиться и так, что сообщение было бы доставлено неверным, но мы бы этого просто не заметили (например, если бы флаги 1-ого, 5-ого и 6-ого леммингов превратились бы в неправильные). Разумно предположить, что вероятность изменения большого количества битов мала по сравнению с изменением одного или нескольких битов. В реальности системы связи намного сложнее и, для того чтобы справиться с трудными случаями, разработаны ещё более сложные коды.
Аналогичные алгоритмы можно использовать и в других местах для проверки корректности информации. Например, различные штрих-коды товаров, личные коды, номера банковских счетов и так далее.

Пять друзей - Ася, Боря, Варя, Гена и Дима - решили сыграть в игру "Испорченный телефон". Ася прошептала Боре состоящее из 10 букв слово по буквам (например, K-A-N-A-D-A-L-A-N-E). Далее Боря прошептал Варе слово по буквам, но допустил одну ошибку. Ошибка может быть в том, что одна буква была заменена на новую букву (например, K-A-R-A-D-A-L-A-N-E) или вообще пропала (например, K-A-N-A-D-A-L-A-E). Потом Варя прошептала Гене слово по буквам, но тоже сделала ошибку, и так далее.
Во время каждой передачи слова делается именно одна ошибка, причём друзья могут сделать ошибку с одной и той же буквой.

Если Ася прошепчет Боре слово V-Õ-I-S-T-L-U-S-E-D по буквам, то какие из следующих слов Гена может прошептать Диме?
[Märkeruudud]
A. V-Õ-S-T-E-S
B. V-Õ-Õ-S-T-L-U-S-E-D
C. V-Õ-I-S-T-L-U-S-E
D. V-I-S-T-N-A-S-D
E. Õ-S-T-L-U-S-E
Правильный ответ B, C и E.
Ася прошепчет Боре правильное слово. Боря допустит одну ошибку и прошепчет неверное слово Варе. Варя тоже допустит одну ошибку и прошепчет это слово Гене. В конце, Гена тоже допустит одну ошибку и прошепчет неверное слово Диме. Таким образом, к моменту, когда Дима услышит слово, будет сделано ровно три ошибки.
Вариант ответа А невозможен. Тут имеется только шесть букв, то есть пропало четыре буквы. Однако в нашем случае максимально пропало только три буквы.
Вариант ответа B возможен. I заменили на Õ - это первая ошибка. Далее заменили любую букву (например, L) - это вторая ошибка. Во время совершения третьей ошибки эта буква была заменена обратно на первоначальную букву (L). Например, V-Õ-I-S-T-L-U-S-E-D → V-Õ-Õ-S-T-L-U-S-E-D → V-Õ-Õ-S-T-M-U-S-E-D → V-Õ-Õ-S-T-L-U-S-E-D.
Вариант ответа C возможен. Пропала буква D. Далее заменили любую букву два раза таким образом, что в итоге восстановилась первоначальная буква. Например, V-Õ-I-S-T-L-U-S-E-D → V-Õ-I-S-T-L-U-S-E → V-Õ-I-S-T-M-U-S-E → V-Õ-I-S-T-L-U-S-E.
Вариант ответа D невозможен. В этом слове только 8 букв, то есть пропало две буквы. Кроме этого, здесь появились две новые буквы (N и A), то есть произошло две замены. Таким образом, в этом варианте сделано больше 3-х ошибок.
Вариант ответа E возможен. Здесь пропало ровно три буквы (V, I и D) и ничего более.
Данное задание демонстрирует помехи при передачи данных. В этом задании в роли помех выступают пропажа и замена букв. Мы знаем, что в этом задании помехи ограничены тремя буквами. Поэтому мы можем быть уверены, что слово, услышанное Димой, содержит по меньшей мере семь букв, которые соответствуют (по порядку) первоначальному слову.
Пример, который больше соответствует действительности в вопросе о возникновении помех при передаче данных, основывается на битах, то есть числах 0 и 1, с помощью которых представлены цифровые сигналы. В таких сигналах также может возникнуть ошибочная замена или пропажа битов. Здесь замена означает замену битов, то есть вместо 0 возникает 1 и наоборот.
Первопроходцем в области того, как передать цифровой сигнал практически без ошибок, был Клод Шеннон. Он также известен как отец теории информации. Клод Шеннон изучал влияние канала на передающиеся по нему сигналы.

Тиму нравится изготавливать картинки по следующим шагам.
1-ый шаг. Он выбирает 4 квадрата с разными орнаментами, например, такие:

2-ой шаг. Он выбирает угол (верхний левый, верхний правый, нижний левый или нижний правый) и от каждого квадрата от отрезает один и тот же угол. Например, если он выберет нижний правый угол, то он получит следующие маленькие квадраты:
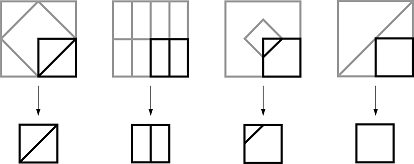
3-ий шаг. Он соберёт все маленькие квадратики, что получились в результате выполнения 2-ого шага, и наложит все орнаменты друг на друга. В результате он получит картинку, как, например, приведена ниже:
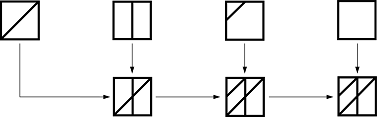
Если он выберет вот такие квадраты

и воспользуется вышеописанным методом, то какую из приведённых картинок он может получить после выполнения всех трёх шагов?
[Raadionupud]
A. 
B. 
C. 
D. 
Правильный ответ C.
Выбрав верхний левый угол, Тим получит картинку

Выбрав верхний правый угол, Тим получит картинку

Выбрав нижний левый угол, Тим получит картинку

Выбрав нижний правый угол, Тим получит картинку
Таким образом, из предложенных вариантов единственным, который Тим сможет получить, будет вариант C. Он получится при выборе нижнего левого угла.
Это задание является примером работы программной модели MapReduce. Эту модель используют для обработки больших объёмов данных с использованием большого количества соединённых между собой компьютеров. Из большого объёма данных информацию добывают с помощью Map функции, а затем всю эту информацию собирают воедино с помощью Reduce функции.
Модель была разработана в Google, но затем она стала также очень популярной за пределами корпорации.

Во время каникул в течение двух недель Марина помогала маме в их домашнем кафе.
Утром каждого понедельника она получила от мамы монеты на сумму 40€. Так как эти монеты предполагалось использовать для того, чтобы давать сдачу, то девочка положила их в кассу.
В конце каждого рабочего дня она записывала, сколько денег уже находится в кассе. Основываясь на собранных данных, она построила график:
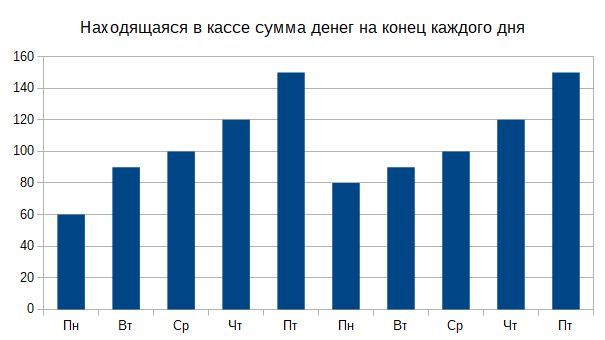
Вечером каждой пятницы она забирала все деньги из кассы и передавала их маме.
Какая была самая большая дневная выручка в евро?
[Tekstikast, täisarv]
Правильный ответ 40€.
Для получения лучшего обзора о доходе кафе построим график. На нём отдельно отметим, что было в кассе каждое утро и каждый вечер (помним, что утром каждого понедельника к первоначальной сумме добавлялось 40€):
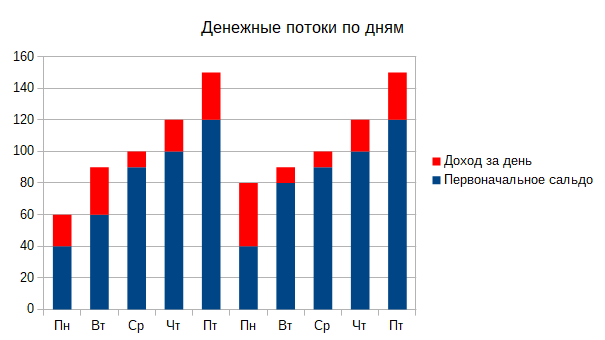
Картина будет более понятной, если с графика уберём данные о состоянии кассы на утро каждого дня и сосредоточимся на доходе, который кафе получало в течение дня:
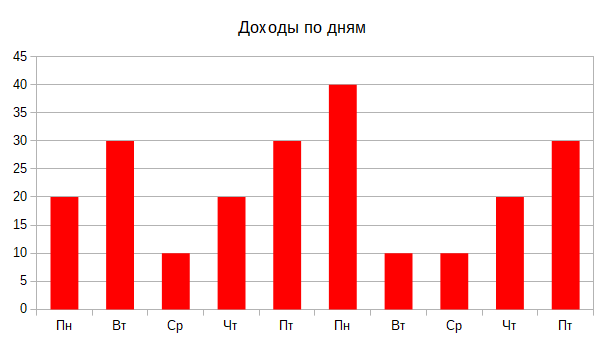
Теперь очевидно, что самая большая дневная выручка была 40€. Эту выручку кафе получило на второй неделе в понедельник.
Данное задание демонстрирует, как способ представления данных может облегчить или усложнить поиск ответа на вопрос. Если используемые для построения графика данные находятся в электронной таблице или базе данных, то необходимые преобразования для лучшего представления данных нам поможет выполнить компьютер. Чем больше данных, тем больше пользы будет от такого автоматического преобразования.

Для поиска слов в тексте можно использовать регулярные выражения (regular expressions). Они могут содержать метасимволы, с помощью которых задают более сложные правила поиска.
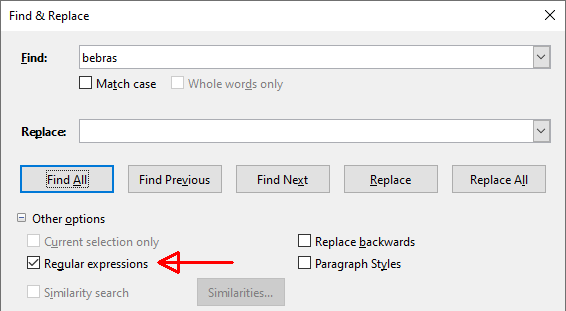
Вот некоторые из метасимволов:
[:space:] – пробелы, например b[:space:]e найдёт текст b e,
? – специальный символ, указывающий, что знак перед ним может в тексте встречаться или отсутствовать, например be?b найдёт beb, а также и bb.
В приведенном ниже тексте слово "bebras" встречается пять раз (выделены жирным шрифтом), и каждый раз оно записано по-разному:
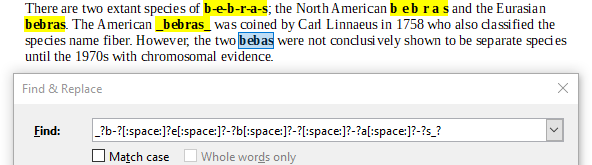
There are two extant species of b-e-b-r-a-s; the North American b e b r a s and the Eurasian bebras. The American bebras was coined by Carl Linnaeus in 1758 who also classified the species name fiber. However, the two bebas were not conclusively shown to be separate species until the 1970s with chromosomal evidence.
Какое регулярное выражение следует ввести в окно поиска, чтобы найти в тексте все пять вариантов слова "bebras"?
[Raadionupud]
A. _?b-?e-?b-?r?-?a-?s_?
B. _?b-?[:space:]?e[:space:]?-?b[:space:]?-?r?[:space:]?-?a[:space:]?-?s_?
C. _?b[:space:]?e[:space:]?b[:space:]?r?[:space:]?a[:space:]?s_?
D. _?b-?[:space:]?e[:space:]?-?b[:space:]?-?[:space:]?-?a[:space:]?-?s_?
Правильный ответ B. _?b-?[:space:]?e[:space:]?-?b[:space:]?-?r?[:space:]?-?a[:space:]?-?s_?.
Рассмотрим каждое выражение по отдельности.
Выражение А не найдёт вариант "b e b r a s", где между буквами имеются пробелы:
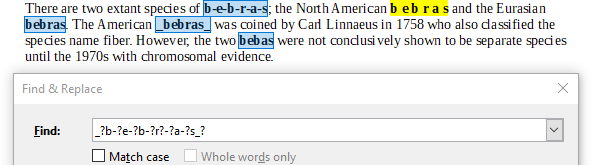
Выражение B найдёт все пять вариантов:
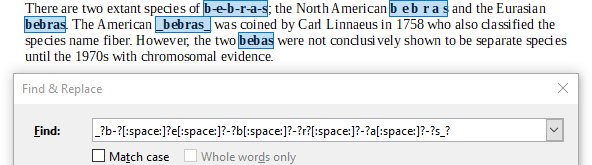
Выражение С не найдёт форму слова со знаком дефиса между буквами:
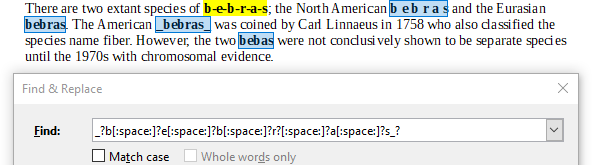
Выражение D найдёт только вариант с пропущенной буквой "r":
Регулярные выражения очень часто используются в программировании, например, для поиска совпадающих символов, множества символов, слов. Также они используются для валидации целых строк, поиска и замены слов или символов. Регулярные выражения также можно использовать для валидации данных, например, когда паролю задаются требования в виде минимального количества символов или наличия маленьких и больших букв, цифр или специальных символов.

Для участия в официальных турнирах все теннисисты должны быть зарегистрированы в государственной теннисной ассоциации. По этой причине каждый клуб ведёт учёт своих игроков и их регистрации, а для этого используются состоящие из строчек и столбцов таблицы. Для каждого игрока отведена одна строчка. На основании этих данных клуб определяет, надо ли какому-нибудь игроку обновить свою регистрацию.
Какая комбинация столбцов будет точно достаточной (то есть содержать в достаточной мере, но не слишком много данных), чтобы определить, надо ли игроку обновить свою регистрацию перед следующим турниром (время проведения которого известно)?
[Raadionupud]
A. Регистрационный номер игрока, дата рождения игрока, срок окончания регистрации
B. Регистрационный номер игрока, плата за регистрацию, срок окончания регистрации
C. Регистрационный номер игрока, дата последнего обновления регистрации, продолжительность периода регистрации
D. Регистрационный номер игрока, дата последнего обновления регистрации, возрастная категория игрока
Правильный ответ C.
На основании даты последнего обновления регистрации и продолжительности периода регистрации мы можем вычислить, когда закончилась регистрация. Регистрационный номер игрока подскажет нам, чью регистрацию необходимо обновить.
Вариант А неправильный, потому что нам не надо знать дату рождения игрока.
Вариант B неправильный, потому что в данном случае нам не надо знать плату за регистрацию.
Вариант D неправильный, потому что в данном случае нам не надо знать возрастную категорию игрока. К тому же, если мы не знаем продолжительность периода регистрации, то знание только даты последнего обновления регистрации нам не поможет определить, когда же заканчивается регистрация.
Сегодня повсеместно распространены таблицы с данными, которые называются базами данных. Информатики должны разрабатывать структуры этих таблиц: какие столбцы обязательны, какой формат обязателен, как данные из одной таблицы будут связаны с данными из другой таблицы. Например, у нас может быть таблица с личными данными игроков. В ней мы найдём имя игрока, его возраст, другие детали по каждому регистрационному номеру. Этот номер является связью между строчкой с личными данными и регистрационными данными игрока.
Конечно, мы должны хорошо обдумать, какие данных необходимо сохранять. В этом процессе мы должны стараться соблюсти равновесие. Если мы соберём недостаточное количество данных, то такая таблица может оказаться бесполезной или с ней будет трудно работать, так как получение ответа на основании имеющихся данных потребует слишком большой вычислительной работы. С другой стороны, если мы соберём слишком много данных, исходя из принципа "на всякий случай", то получим целую кучу данных, бессмысленно потратим место памяти и, в итоге, можем получить даже противоречивые ответы. Например, если дата последнего обновления регистрации, продолжительность периода регистрации и дата окончания регистрации не будут совпадать. Также возможны проблемы с безопасностью данных. Поэтому-то в информатике используются методы (например, нормализация), с помощью которых определяется подходящая структура для табличных данных.

У Яши блокнот в клеточку. Он решил нарисовать в нём состоящую из последовательно расположенных чисел спираль. Яша начал рисовать с клеточки, координатой которой является (0; 0):

Например, координатами числа 19 будет (-2; 0), числа 27 - (+3; +1), а числа 31 - (+3; -3).
В какой-то момент ему надоело записывать все цифры. Он решил узнать, где же будет располагаться его любимое число 66. Помоги ему!
Каковы будут координаты числа 66, если Яша продолжит последовательно записывать числа в спираль?
[Koordinaatide paar (X;Y)]
Правильным ответом будет (-4; -3).
Правильный ответ мы можем увидеть на следующем рисунке:
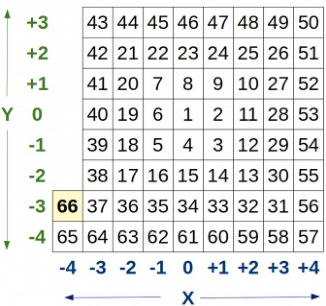
В основе алгоритмического мышления лежит умение распознавать шаблоны (patterns). В нашем случае пространственный шаблон напоминает спираль - кривую, которая выходит из одной точки (в данном случае она располагается в точке (0; 0)) и перемещается вокруг первоначальной точки, причём вращаясь и удаляясь от неё всё дальше. Спирали часто встречаются в природе - это могут быть, например, ракушки или галактики.
Обычно местоположение точки в пространстве указывается с помощью координат. В нашем задании использовалась прямоугольная система координат, которая измеряет удалённость точек от начальной точки по горизонтали и вертикали.

Пространство для хранения данных на жёстком диске разделено на кластеры определённого размера. При сохранении файл всегда занимает целое число кластеров. Если размер файла не делится на размер кластера, то часть последнего занятого файлом кластера просто остаётся неиспользованной.
На приведённом рисунке изображено использование жёсткого диска, поделённого на кластеры размером 16 KB - использованные кластеры обозначены серым цветом, а пока ещё свободные кластеры - белым.
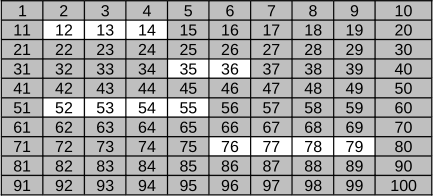
На диск по одному записываются следующие файлы: прежде всего файл A размером 20 KB, затем файл B размером 18 KB, потом файл C размером 34 KB и наконец файл D размером 48 KB. Во время сохранения файла операционная система старается найти свободные кластеры, которые бы располагались один за другим. Это делается с целью избежать фрагментации файлов, то есть распределения файла между разными частями диска, что уменьшает продуктивность компьютера.
Один из подходов для уменьшения фрагментации файлов заключается в следующем.
Найти набор расположенных один за другим свободных кластеров, куда поместился бы весь файл.
Если такого набора нет, то распределить файл таким образом, что имеющиеся куски можно было бы расположить в первые попавшиеся кластеры.
Как выглядит файловая система после того, как по описанным выше правилам записываются файлы A (красный), B (зелёный), C (синий) и D (жёлтый)?
[Raadionupud]
A. 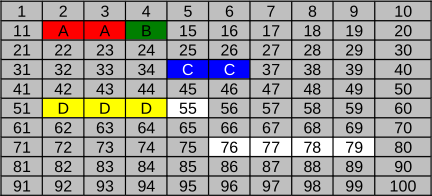
B. 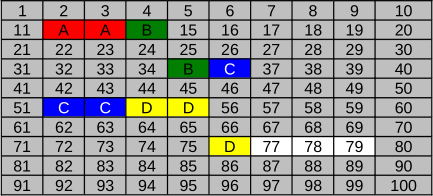
C. 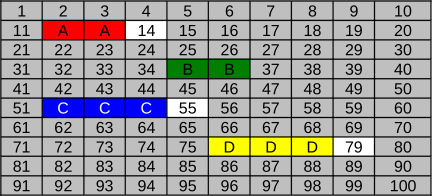
D. 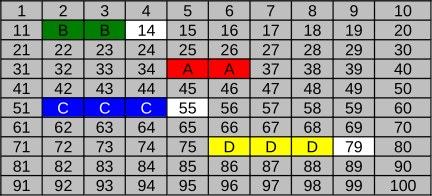
Правильный ответ C.
Файл A (20 KB) записывается в кластеры 12 и 13 (в них имеется 32 KB свободного места).
Файл B (18 KB) записывается в кластеры 35 и 36 (в них имеется 32 KB свободного места). Кластер 14 останется неиспользованным, так как его использование привело бы к фрагментации файла B. Использовав кластеры 35 и 36, мы избежим этой проблемы.
Файл C (34 KB) записывается в кластеры 52, 53 и 54 (в них имеется 48 KB свободного места).
Файл D (48 KB) записывается в кластеры 76, 77 и 78 (в них имеется 48 KB свободного места).

Вариант А не будет правильным ответом. Согласно этому варианту, файл B займёт только один кластер. Так как размер кластера равен 16 KB, то невозможно в один кластер уместить файл размером 18 KB. Аналогично, нельзя уместить файл C в два кластера.
Вариант B не будет правильный ответом. Согласно этому варианту, при сохранении файл B был фрагментирован - однако, следуя правилу №1 (MÄRKUS: kas see on 1. või 2. reegle?), этого делать нельзя, если найдётся некоторое количество свободных расположенных друг за другом кластеров с достаточным размером. Аналогично, файлы C и D были бы бессмысленно фрагментированы.
Вариант D не будет правильным ответом. Согласно этому варианту, файл A сохранили в кластеры 35 и 36, хотя на момент записи кластеры 12 и 13 были свободны. Следуя правилу №1, файл А следовало записать в первую область с подходящим размером.
Данное задание демонстрирует нам, как хранится информация на жёстком диске, и объясняет, что же такое фрагментация файлов.
В примере этого задания мы уже видим, что начальное состояние файловой системы подверглось внешней фрагментации. Это привело к тому, что на диске мало расположенных рядом друг с другом свободных кластеров. Внешняя фрагментация возникает тогда, когда создаются, изменяются или удаляются файлы различных размеров.
Когда создаётся один большой файл, а на диске нет достаточного количества свободных расположенных рядом друг с другом кластеров, то файл дробится на маленькие части, которые затем записываются в файловую систему. Этот процесс называется фрагментацией файла. Минусом такого процесса является уменьшение продуктивности жёсткого диска.
Третий тип фрагментации встречается в управлении оперативной памятью (RAM) компьютера. Оперативная память также разделена на страницы с определённым размером, и её распределение между программами также происходит по страницам. Обычно программа использует несколько страниц, причём зачастую последняя страница не бывает заполнена до конца. В результате в памяти остаётся свободное пространство, которым другие программы, к сожалению, не могут воспользоваться. Это называется внутренней фрагментацией.
Copyright © 2020 Bebras – International Challenge on Informatics and Computational Thinking.
Licensed under Creative Commons Attribution-ShareAlike 4.0 International License.
Flag icons by GoSquared.