1. Turingi masin

Turingi masin on arvuti teoreetiline mudel. Masin koosneb lindist, millel on sümbolid, ning lugemis-kirjutamispeast. Pea võib masina töö ajal liikuda ühe sümboli kaupa paremale või vasakule:

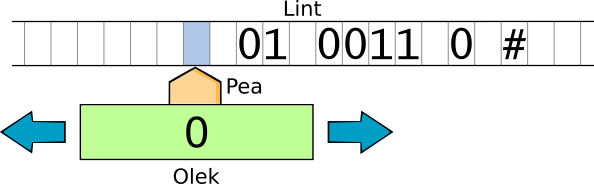
Masin on töö ajal kogu aeg mingis olekus ja tema tööd juhib programm, mida võib esitada viieveerulise tabelina:

Praegune olek Loetud sümbol Uus sümbol Liikumise suund Uus olek
0 _ _ → 0
0 0 _ → 0
0 1 1 → 1
0 # # → lõpp
1 _ _ → 0
1 0 0 → 1
1 1 1 → 1
1 # # → lõpp

Masin alustab oma tööd alati olekus 0 ja edasi käitub järgmiselt:

Märk "_" tabeli teises või kolmandas veerus tähendab tühikut. Olek "lõpp" tähendab, et masin lõpetab töö. Tühjad read on tabelis ainult loetavuse parandamiseks.

Eelolevas näites toodud programm liigub lindil vasakult paremale, kustutab kahendarvude algusnullid ja lõpetab töö trellimärgi järel:

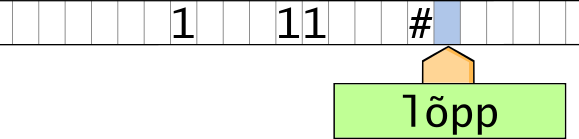
Täpsemalt, alustades olekus 0, näeb masin lindil tühikut ja liigutab tabeli esimese rea kohaselt lugemis-kirjutamispea paremale, jäädes olekusse 0. See kordub, kuni masin jõuab esimese nullini. Tabeli teise rea kohaselt kirjutab ta siis nulli asemele tühiku ja liigutab pea edasi paremale, püsides endiselt olekus 0. Nüüd leiab ta esimese ühe. Tabeli kolmanda rea kohaselt jätab ta selle muutmata, liigutab pea jälle paremale, aga läheb ise olekusse 1. Järgmisena loeb masin lindilt esimese ühe järel oleva tühiku. Vastavalt tabeli alt neljandale reale jätab ta selle muutmata ja läheb tagasi olekusse 0. Samal moel jätkates lõpetabki masin töö eeloleval joonisel näidatud seisus.

Küsimus

Mida teeb järgmine programm?

Praegune olek Loetud sümbol Uus sümbol Liikumise suund Uus olek
0 1 1 → 1
0 * * → 0
1 1 1 → 2
1 * F → lõpp
2 1 1 → 1
2 * T → lõpp

Märk "*" teises veerus tähendab "mistahes muu sümbol" ja sellele vastavat rida kasutatakse, kui ükski teine ei sobi; märk "*" kolmandas veerus tähendab, et lindile kirjutatakse tagasi sama sümbol, mis sealt loeti.

[Raadionupud]

A. Asendab lindil ühed kahtedega

B. Asendab lindil kahed ühtedega

C. Otsib lindilt ühtedest koosnevat gruppi ja kirjutab lindile "T" (true, tõene), kui grupis on paarisarv ühtesid, või "F" (false, väär) vastasel juhul

D. Otsib lindilt ühtedest koosnevat gruppi ja kirjutab lindile "T" (true, tõene), kui grupis on paaritu arv ühtesid, või "F" (false, väär) vastasel juhul

Vastus

Õige vastus on: C.

2. Porgandirobot

Talus on põllul porgandid viies reas, igas reas seitse porgandit:

Talus on ka robot, mida saab programmeerida porgandeid koristama järgmiste käskudega:

Käsk Tähendus
P Võta üles enda ees olev porgand
F Liigu üks samm (üks rea- või veeruvahe) edasi
R Pööra 90 kraadi paremale
L Pööra 90 kraadi vasakule

Kui mingit käsku või käskude gruppi on vaja korrata, võib selle ette kirjutada korduste arvu. Näiteks 3F tähendab, et robot liigub kolm sammu edasi ja 4(F R) tähendab, et robot liigub ruudukujuliselt ja naaseb algsesse asukohta.

Küsimus

Milline järgmistest programmidest sobib, et robot kõik porgandid üles võtaks?

[Raadionupud]

A. 2(P 6(F P) R F R) (P 6(F P) L F L) 7P

B. R 3(P 4(F P) L F L) (P 4(F P) R F R)

C. 2(P 6(F P) R F R P 6(F P) L F L) P 6(F P)

D. 5(7P L F R) 7P

Vastus

Õige vastus on: C.

3. Uus haigla

Ühes riigis on kuus suuremat linna. Alloleval kaardil on näidatud sõiduajad erinevate linnade vahelistel teedel:

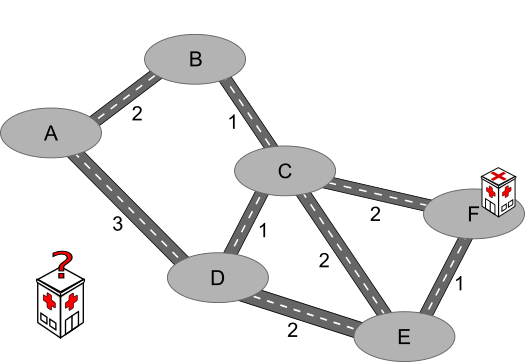
Praegu on haigla ainult linnas F ja see tähendab, et halvimal juhul (kui haigestub linna A elanik) tuleb haiglasse sõiduks kulutada 5 tundi.

Küsimus

Kuhu tuleks ehitada teine haigla, et halvimal juhul haiglasse jõudmiseks kuluv aeg oleks vähim võimalik?

[Raadionupud]

A. Linna A

B. Linna B

C. Linna C

D. Linna D

E. Linna E

Vastus

Õige vastus on: B.

4. Pingimeister

Albert valmistab pinke. Igal pingil peab olema neli ühepikkust jalga. Erinevatel klientidel on erinevad soovid, sellepärast teeb Albert mitmesuguste kõrgustega pinke:

Albert kogub pinkide jalgadeks materjali metsas ja leitud materjal on sageli erineva pikkusega. Vajadusel võib Albert pikemaid jalgu lühendada (jala lühendamisel on ainult üks osa sellest kasutatav):

Kuna jalgade lühendamine on töömahukas, tahab Albert seda võimalikult vähe teha.

Albertil on praegu laos järgmised 32 jalga:

Pikkus Arv
10 3
9 6
8 3
7 3
6 5
5 3
4 3
3 2
2 4

Küsimus

Mis on vähim võimalik lühendatavate jalgade arv, et saada kokku materjal kaheksa pingi valmistamiseks?

[Täisarv]

Vastus

Õige vastus on: 6.

5. Kiire kohtumine

Kahel sõbral on vaja kiiresti kohtuda. Jalgsi jõuavad nad oma asukohast samas reas või veerus olevale naaberruudule täpselt ühe minutiga. Ratta või auto juurde jõudes saavad nad edasi liikuda kiiremini: rattaga kaks ja autoga viis ruutu minutis. Üle vee ei saa nad liikuda ühegi vahendiga.

Küsimus

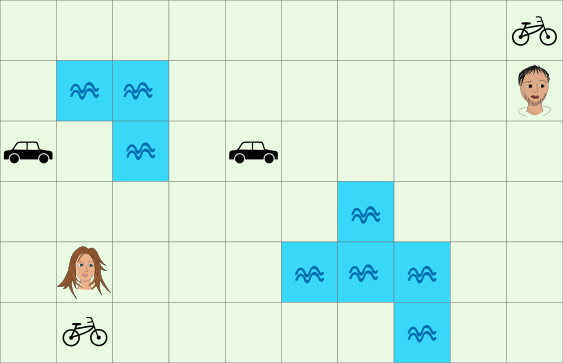
Mis on vähim aeg minutites, millega neil on võimalik jõuda samale ruudule?

[Täisarv]

Vastus

Õige vastus on: 4.

6. Kaelakee kirjeldus

Jean armastab kaelakeid meisterdada. Ta tahab oma keede kirjeldusi ka sõpradega jagada ja kasutab selleks omaloodud keelt.

Iga helmest märgib selle kujule vastav täht S (star, viisnurk), T (triangle, kolmnurk), R (rectangle, nelinurk), L (line, kriips). Lihtsalt helmeste järjest üles kirjutamise asemel kasutab Jean kavalamat skeemi:

  • kui kees on järjest mitu ühesugust helmest, võib kirjutada helmeste arvu ja selle järele helme tähise;
  • kui kees on korduv lõik, võib kirjutada kordumiste arvu ja selle järele sulgudesse lõigu kirjelduse.

Näiteks kee

üks võimalik kirjeldus on S3(TR)3SL. Selle kirjelduse pikkus on 9 märki.

Küsimus

Mitu märki on alloleva kee minimaalse pikkusega kirjelduses (loetakse nii tähti, numbreid kui ka sulge)?

[Raadionupud]

A. 12 märki

B. 13 märki

C. 14 märki

D. 15 märki

Vastus

Õige vastus on: B (13 märki).

7. Pöialpoisid

Lumivalgeke ja seitse pöialpoissi elavad koos ühes majas. Lihtsuse mõttes viitame pöialpoistele nende mütsidel olevate arvudega:

Pöialpoistel olid just mõned tülid ja nüüd on seis selline, et 12 on sõber 1 ja 2-ga, 13 on sõber 1 ja 3-ga, 23 on sõber 2 ja 3-ga ning ainult 123 on endiselt kõigiga sõber.

Pöialpoiste rahustamiseks pakkus Lumivalgeke välja mängu, kus ta hõikab numbri ja pöialpoisid liiguvad vastavalt sellele majja sisse või majast välja järgmiselt:

  • Kui Lumivalgeke hõikab "2", lähevad 2 ja tema sõbrad (12, 23 ja 123) majja sisse.
  • Kui Lumivalgeke hõikab "3", lähevad 3 ja tema sõbrad (13, 23 ja 123) majja sisse.
  • Kui Lumivalgeke hõikab "4", vahetavad 1 ja tema sõbrad asukohta (kes oli enne sees, läheb välja; kes oli enne väljas, läheb sisse).
  • Kui Lumivalgeke hõikab "5", vahetavad 2 ja tema sõbrad asukohta.
  • Kui Lumivalgeke hõikab "6", vahetavad 3 ja tema sõbrad asukohta.

Näiteks kui 1, 2 ja 12 on majas ja ülejäänud väljas ning Lumivalgeke hõikab "5", lähevad 2 ja 12 välja, 23 ja 123 sisse ja ülejäänud jäävad sinna, kus nad olid.

Praegu on kõik seitse pöialpoissi majas, aga Lumivalgeke tahaks nad välja saata ja printsiga kahekesi aega veeta.

Küsimus

Mis on lühim võimalik numbrijada, mille hõikamisega Lumivalgeke kõik pöialpoisid majast välja saab?

Sisesta ainult numbrid ilma tühikute või muude märkideta!

[Tekst]

Vastus

Õige vastus on: 42536 või 43625.

8. Mõttemeister

Jüri mängib oma arvutis mängu Mõttemeister. Arvuti genereerib neljast erinevast numbrist koosneva salasõna. Mängija püüab salasõna ära arvata, tehes pakkumisi. Iga pakkumise peale vastab arvuti, mitu numbrit pakkumises on sellised, mis esinevad ka salasõnas, ja kas need numbrid on pakkumises samadel kohtadel kui salasõnas.

Jüri on seni teinud viis pakkumist ja saanud neile järgmised vastused:

Pakkumine Vastus
5720 Üks õige number õigel kohal
6031 Üks õige number, aga valel kohal
1485 Kaks õiget numbrit, aga mõlemad valel kohal
1596 Pole ühtki õiget numbrit
8125 Üks õige number, aga valel kohal

Küsimus

Milline on salasõna?

Sisesta neli numbrit ilma tühikuteta!

[Tekstikast]

Vastus

Õige vastus on: 3748.

9. Rühmatöö

Kaheksa õpilast jagunevad rühmatööde tegemisel tavaliselt kolmeks:

Alloleval joonisel tähistab iga punkt üht õpilast ja punkti värv näitab, millises rühmas ta tavaliselt on:

Iga joon ühendab kaht õpilast, kes eelistavad tööd teha eraldi rühmades.

Täna aga on üks laud katki ja õpilased tuleb jagada kaheks rühmaks. Seda on võimalik teha nii, et ainult kaks teineteisele vastumeelset õpilast peavad olema samas rühmas.

Küsimus

Millise numbriga joonele vastav paar peab teineteisega leppima, et oleks võimalik kõik õpilased kahte rühma jagada?

[Täisarv]

Vastus

Õige vastus on: 7.

10. Mustrid

Igaühe kolmest eelolevast mustrist saab koostada mingi ühe ruudukese kordusena. Selleks peab ruudukesel olema üks oluline omadus.

Küsimus

Millisel allolevatest ruudukestest seda omadust ei ole?

[Raadionupud]

A. B. C. D.

Vastus

Õige vastus on: C.

11. Ideaalne temperatuur

Kobras Theophilus jälgib pidevalt vee temperatuuri ja märgib tulemused üles. Ta kirjutab alati üles esimese mõõtmistulemuse kohe pärast ärkamist ja viimase enne magamaminekut. Kuna ta teab, et temperatuur muutub kogu aeg tasapisi, kirjutab ta päeva jooksul üles ainult ekstreemsed tulemused: sellised, kus nii eelmine kui ka järgmine on mõlemad madalamad või kui nii eelmine kui ka järgmine on mõlemad kõrgemad. Näiteks kui temperatuur muutuks päeva jooksul nii, nagu näidatud alloleval joonisel, kirjutaks Theophilus üles ainult arvud A, B, C, D ja E.

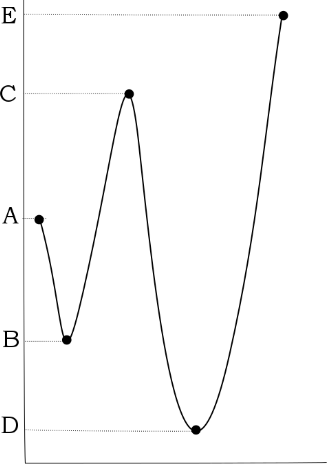
Eile kirjutas Theophilus üles järgmised mõõtmistulemused:
5,1; 5,8; 5,5; 5,9; 5,3; 5,7; 5,4; 5,8; 5,6.

Theophilusel on üks kindel lemmiktemperatuur, mille juures ta tunneb ennast kõige paremini. Eilse päeva jooksul esines see temperatuur täpselt viis korda.

Küsimus

Milline on nende andmete põhjal vahemik, millesse Theophiluse ideaaltemperatuur jääb?

Sisesta miinusega eraldatult vahemiku alumine ja ülemine piir, näiteks 5,1-5,6!

[Tekstikast]

Vastus

Õige vastus on: 5,4-5,5.

12. Burrows-Wheeleri teisendus

Vaatleme järgmist algoritmi antud sõna teisendamiseks:

  1. lisada sõna lõppu marker *;
  2. teha loend saadud teksti kõigist võimalikest tsüklilistest nihetest;
  3. sorteerida loend tähestikuliselt (lugedes markeri * tähestiku lõpus olevaks);
  4. lugeda tulemuseks tekstide viimased märgid sorteeritud loendis.

Teksti tsükliliseks nihkeks nimetatakse teksti, mis saadakse nii, et võetakse teksti algusest mõned märgid ja pannakse nad (järjekorda muutmata) teksti lõppu.

Kui näiteks rakendame seda algoritmi sõnale BANANA, saame tulemuseks BNN*AAA:

Markeriga tekst Tsüklilised nihked Sorteeritud loend Lõplik tulemus
BANANA* BANANA* ANANA*B BNN*AAA
ANANA*B ANA*BAN
NANA*BA A*BANAN
ANA*BAN BANANA*
NA*BANA NANA*BA
A*BANAN NA*BANA
*BANANA *BANANA

Küsimus

Milline on tulemus, kui rakendada seda algoritmi sõnale BEBRAS?

Sisesta vastuseks vajalikud märgid ilma tühikuteta!

[Tekstikast]

Vastus

Õige vastus on: R*EBBAS.

13. Tõeväärtustabel

Tõeväärtustabel kirjeldab mingi loogilise avaldise väärtust (○ või ●) selle muutujate kõigi võimalike väärtuste korral. Näiteks järgmises tabelis on ühe avaldise väärtused muutujate x, y ja z kõigi võimalike tõeväärtuste korral:

x y z Tulemus
○ ○ ○ ○
○ ○ ● ●
○ ● ○ ○
○ ● ● ○
● ○ ○ ●
● ○ ● ●
● ● ○ ●
● ● ● ●

Tabelis kirjeldatud avaldise võiksime üles kirjutada ka valemina, loetledes järjest kõik sisendid, mille korral tulemus on ●:

(x=○ and y=○ and z=●) or
(x=● and y=○ and z=○) or
(x=● and y=○ and z=●) or
(x=● and y=● and z=○) or
(x=● and y=● and z=●)

Sellise esituse korral peame avaldise üles kirjutamiseks viitama muutujatele kokku 15 korda.

Kui tabelit natuke tähelepanelikumalt vaadata, võime märgata, et kui x=●, siis on ka tulemus alati ●, ja sellest lähtuvalt lühendada valemit nii, et see viitab muutujatele vaid neli korda:

(x=○ and y=○ and z=●) or 
(x=●)

Aga see pole veel piir. Piisab ka ainult kolmest muutujaviitest:

(y=○ and z=●) or 
(x=●)

Viimase valemi kaht rida võime graafiliselt kujutada järgmiselt:

Küsimus

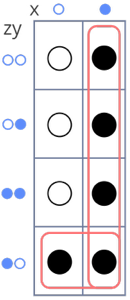
Vaatleme nüüd suuremat tabelit

a b c d Tulemus
○ ○ ○ ○ ○
○ ○ ○ ● ○
○ ○ ● ○ ○
○ ○ ● ● ○
○ ● ○ ○ ○
○ ● ○ ● ○
○ ● ● ○ ●
○ ● ● ● ○
● ○ ○ ○ ●
● ○ ○ ● ●
● ○ ● ○ ●
● ○ ● ● ●
● ● ○ ○ ●
● ● ○ ● ●
● ● ● ○ ●
● ● ● ● ○

ja selle graafilist esitust (pannes tähele ka muutujate c ja d järjekorda):

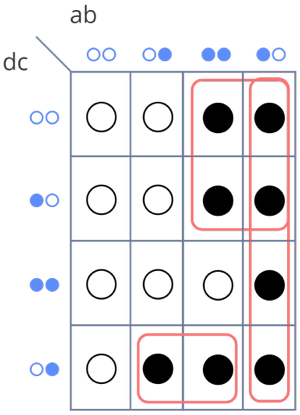
Mis on minimaalne muutujaviidete arv selle avaldise esitamiseks valemina?

[Täisarv]

Vastus

Õige vastus on: 7.

14. Piltide pakkimine

Rastergraafikas esitatakse pilte väikestest ühevärvilistest ruutudest (pikselitest) koosnevate mosaiikidena. Must-valges pildis võib iga piksel olla kas must või valge, mida tavaliselt tähistatakse vastavalt arvudega 0 ja 1.

Selleks, et vähendada piltide salvestamiseks vajalikku andmemahtu, kasutatakse erinevaid pakkimismeetodeid. Allolev joonis illustreerib üht lihtsat meetodit must-valgete piltide pakkimiseks.

Iga rea esimene arv näitab järjestikuste valgete pikselite arvu (kui esimene piksel on must, siis algab rida arvuga 0) ja edasi on vaheldumisi mustade ja valgete pikselite arvud.

Küsimus

Millist pilti kodeerivad järgmised andmed?

15
5, 3, 7
4, 1, 3, 1, 6
3, 1, 5, 1, 5
2, 1, 7, 1, 4
1, 1, 4, 1, 4, 1, 3
1, 1, 3, 3, 3, 1, 3
1, 1, 4, 1, 4, 1, 3
2, 1, 7, 1, 4
3, 1, 5, 1, 5
4, 1, 3, 1, 1, 1, 4
5, 3, 3, 1, 3
12, 1, 2
13, 1, 1
15

[Raadionupud]

A. 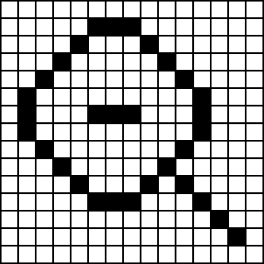B.

C. D.

Vastus

Õige vastus on: B.

15. Noogutuste loendamine

Teadusmuuseumi uus piletiautomaat kasutab külastajatega suhtlemiseks raalnägemissüsteemi. N pileti ostmiseks peab külastaja seisma automaadi ette, noogutama N korda allapoole ja siis tõstma pea ülespoole.

Raalnägemissüsteem jälgib külastaja ninajuure näivat pikkust (allolevatel kujutistel punane joon) muutujas nose ja otsustab selle järgi tema pea asendi üle:

Kujutis Selgitus
Kui nose väärtus on 1, on pea otse
Kui nose väärtus on üle 1 (joonisel nose = 1.3), on pea suunatud allapoole
Kui nose väärtus on alla 1 (joonisel nose = 0.7), on pea suunatud ülespoole

Piletimüügi programm käivitatakse, kui järjekordne külastaja astub kaamera ette ja vaatab otse.

Küsimus

Milline järgmistest programmidest müüb külastajale õige arvu pileteid?

[Raadionupud]

A. B.

C. D.

Vastus

Õige vastus on: D.

Copyright © 2020 Bebras – International Challenge on Informatics and Computational Thinking.
Licensed under Creative Commons Attribution-ShareAlike 4.0 International License.

Flag icons by GoSquared.