

Benno töötab Kopra Metallivabrikus mutrite ja poltide koosteliinil.

Tema töökirjeldus on selline:
Asjad võivad Benno jaoks valesti minna kahel viisil:
Milline järgnevatest mutrite  ja poltide
ja poltide  jadadest konveieril (vasakult paremale) ei põhjusta viga Benno töös?
jadadest konveieril (vasakult paremale) ei põhjusta viga Benno töös?
[Raadionupud]
A. 
B. 
C. 
D. 
Õige vastus on: C.
Variandi C puhul võime jälgida olukorda korvis ja konveierlindil näiteks tabeli abil, kui M tähistab mutrit  ja P polti
ja P polti  :
:
| Korv | Konveierlint |
|---|---|
| tühi | M P M M P M M P P P |
| M | P M M P M M P P P |
| tühi | M M P M M P P P |
| M | M P M M P P P |
| M M | P M M P P P |
| M | M M P P P |
| M M | M P P P |
| M M M | P P P |
| M M | P P |
| M | P |
| tühi | tühi |
Variandis A tekib viga pärast jada "M P P", kuna teise poldi saamise hetkel pole korvis ühtki mutrit.
Variandis B tekib viga pärast jada "M M P M M P P P P", kuna siin pole viienda poldi saamise hetkel korvis enam ühtki mutrit (enne seda on lindilt tulnud ainult 4 mutrit).
Variandis D tekib viga peale terve rea läbimist, kuna lindil on 6 mutrit ja 4 polti ning seega jääb 2 mutrit alles.
Ülesanne on näide nn. pinuautomaadist (ingl push-down automaton, PDA). Selline automaat on üheks võimaluseks kirjeldada algoritmi, mis põhineb olekutel ning millel on piiramatu hulk mälu nn pinuna (ingl stack): viimasena lisatud elemendid võetakse sellest esimesena. Käesoleval juhul iseloomustab olekut see, kas järgmisena tuleb lindilt mutter või polt, pinu aga esindab mutrite hoidmiseks mõeldud korv.
Pinuautomaati kasutatakse näiteks kontekstivabade keelte tuvastamiseks ja analüüsimiseks. Keele analüüsimine tähendab muuhulgas selgitada välja, kas antud sümbolite jada on antud keele jaoks sobiv ehk kas see kuulub antud keelde. Praeguse ülesande puhul me võime mõelda mutritest ja poltidest kui sulgudest ja nende tasakaalustamisest, kus M on algav sulg ("(") ja P lõppev sulg (")"). Sulgude tasakaal tähendab sulgude reeglitele vastavat järjekorda aritmeetilises avaldises. Näiteks jadades "(((()" ja "())(" pole sulud tasakaalus. Sulgude tasakaalu tuvastamine on tähtis kompilaatorite jaoks, kuna mõned programmeerimiskeeled kasutavad sulgusid lisaks aritmeetilistele avaldistele ka programmi struktuuri märkimiseks.

Jaanil on kolme värvi kuusnurkseid pusletükke. Kui ta paigutab kolm tükki kõrvuti alloleval joonisel näidatud kolmnurgana, peavad need tükid olema kas kõik sama värvi või kõik erinevat värvi.
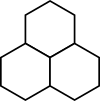
Jaan alustab pusletükkidest torni ehitamist. Ta laob selle alumise rea, nagu on näha alloleval joonisel.
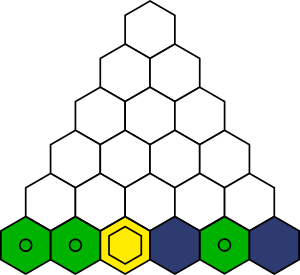
Millist värvi tuleb torni kõige ülemine tükk, kui Jaan peab torni lõpuni kinni kolmnurgareeglist?
[Raadionupud]
A. 
B. 
C. 
D. Võimalusi on rohkem kui üks
Õige vastus on: B.
Kui me teame kahe kõrvutise kuusnurga värvi, siis need määravad ära ka vahetult nende kohal oleva tüki värvi. Näiteks võtame alumise vasakpoolse tüki neist, mille värvi me veel ei tea. Kuna kaks kuusnurka tema all on mõlemad rohelised, peab ka see olema roheline. Aga näiteks sellest paremale jääv tükk peab olema sinine, kuna selle alla jääb üks roheline ja üks kollane tükk.
Samal moel jätkates võime liikuda üles torni tippu ja tulemus on selline:
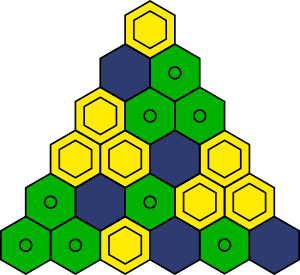
Paneme tähele, et me jõuame sama tulemuseni sõltumata sellest, kummast torni äärest me iga rea analüüsimist alustame.
Leidsime, et see, kumba kahest variandist kasutada, sõltub kahe alloleva kuusnurga värvist: kas need on sama või erinevat värvi. Samal moel kordame valikut, kuni kõigi torni tükkide värv on teada. Selline sammude järjekord moodustab algoritmi, mida me kasutame selle ülesande lahendamiseks. Kui me kirjutaksime analoogse programmi, siis kahe variandi vahel valimine vastab tingimuslausele, selle valiku tegemine järjest iga tüki jaoks aga korduslausele.
Algoritmide koostamine ja nende programmidena realiseerimine on informaatikute üks kesksemaid ja tähtsamaid ülesandeid. Selleks vajame nii otsustusmustri leidmist kui ka loogikat ülesande osadeks jagamisel.

Igal aastal korraldatakse Koprapääl suusavõistlusi. Neist võtab osa ka Moonika, kellel on suur soov sel aastal võita. Moonika on nimekirjas viimane võistleja. Selleks, et võita, peab tema sõiduaeg olema väiksem kui senisel liidril.
Allolev kaart näitab mäenõlval olevaid suusaradu. Finišisse jõudmiseks võivad võistlejad sõita ainult mööda radu allapoole, aga iga sõitja võib ise valida, milliseid radu mööda ta laskub. Iga raja juures on minutite arv, mis Moonikal kulub selle läbimiseks.
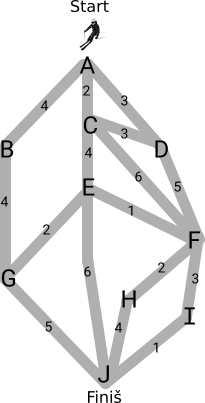
Millist teed mööda peaks Moonika sõitma, et võita, kui senise liidri aeg on 12 minutit?
(Kirjuta Moonika tee punktist A punktini J sellele jäävate tähtede jadana ilma muude märkideta, näiteks ABGJ.)
[Tekstikast]
Õige vastus on: ACEFIJ.
Võistluse võitmiseks peab Moonika leidma sellise rajalõikude järjekorra, mis viib ta stardist A finišisse J lühema ajaga kui 12 minutit. Ta peab alustama stardipunktist ehk punktist A. Sellest saab alguse 3 rada, mis viivad punktidesse B, C ja D vastavalt 4, 2 ja 3 minutiga. Moonika kirjutab need arvud iga punkti juurde üles kui seni kõige kiiremad ajad neisse jõudmiseks. Edasi vaatame punkte nendesse jõudmise aegade järjekorras.
Seega jätkame punkti A järel punkti C uurimisega. Punktist C lähevad rajad punktidesse D, E ja F sõiduajaga vastavalt 3, 4 ja 6 minutit. (Punkti A tagasi minek oleks mäest üles sõitmine ja ei vastaks võistluse tingimustele.) Koguaeg A→C→D läbimiseks on seega 2+3=5, A→C→E läbimiseks 2+4=6 ja A→C→F läbimiseks 2+6=8 minutit. Kuna eelmisest sammust meelde jäänud otsetee A→D ajaga 3 minutit on kiirem kui A→C→D, jääb arv punkti D juures muutmata, aga punkti E juurde kirjutab Moonika 6 ja punkti F juurde 8.
Jätkame radadega, mis algavad punktist D. Ainus, mida on mõtet kaaluda, on punkt F, mille juurde on senini märgitud arv 8. Aeg A→D→F on taas 8 minutit ja see midagi ei muuda. Seejärel kaalub Moonika punktist B algavaid radu, mida on samuti ainult üks. A→B→G sõiduaeg on 8 minutit, mille Moonika märgib punkti G juurde.
Seni on Moonika vaadanud läbi punktidest A, B, C ja D algavad rajad. Järgmisena vaatame punkti E, kuhu jõudmiseks kulub 6 minutit. Seega võtab E kaudu punkti G jõudmine aega 6+2=8, punkti J jõudmine 6+6=12 ja punkti F jõudmine 6+1=7 minutit. Punkti G jõudmine võtab võrdselt 8 minutit nii läbi E kui läbi B. Tee A→C→E→F on vaid 7 minutit ehk lühem kui seni leitud A→D→F. Läbi E punkti J jõudmine võtab aega 12 minutit, kuid Moonikal on võitmiseks vaja saada sellest parem aeg. Kui teeme punkti F puhul läbi sama mõttekäigu, jõuaksime punkti I ajaga 7+3=10 ja punkti H ajaga 7+2=9 minutit.
Läbi punkti G jõuaksime punktini J 8+5=13 minutiga ja see meid ei rahulda. Järgmine variant oleks rada H ja J vahel, kuid ka selle puhul oleks aeg 9+4=13 minutit. Viimaks vaatame ka rada I→J (ehk kogu rada A→C→E→F→I→J) ning näeme, et sel viisil läbime me raja Moonika jaoks võidukalt ehk 11 minutiga. See lahendus on näha ka alloleval joonisel.
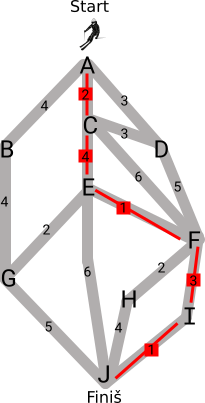
Siin on tegemist graafis lühima tee leidmise ülesandega.
Arvutiteaduses nimetatakse punktidest ja neid ühendavatest lõikudest koosnevaid süsteeme graafideks. Graafiteoorias tähendab lühima tee ülesanne graafi kahe punkti ehk tipu vahel sellise tee leidmist, milles läbitud lõikude ehk servade kaalude summa oleks võimalikult väike.
Mäesuusatamises liigutakse ainult mäest alla ja siis öeldakse, et tegemist on suunatud graafiga. Mõnes teises ülesandes võidakse igal teelõigul liikuda mõlemas suunas ja siis öeldakse, et tegemist on suunamata graafiga.
Lühima tee ülesande lahendamiseks on leiutatud hulk algoritme. Eelpool leidsime lahenduse Dijkstra algoritmi abil, aga lisaks on olemas ka näiteks Bellmanni-Fordi algoritm ja A* (ingl A-star) algoritm.

Kilpkonn ja jänes jooksevad joonisel näidatud rajal:
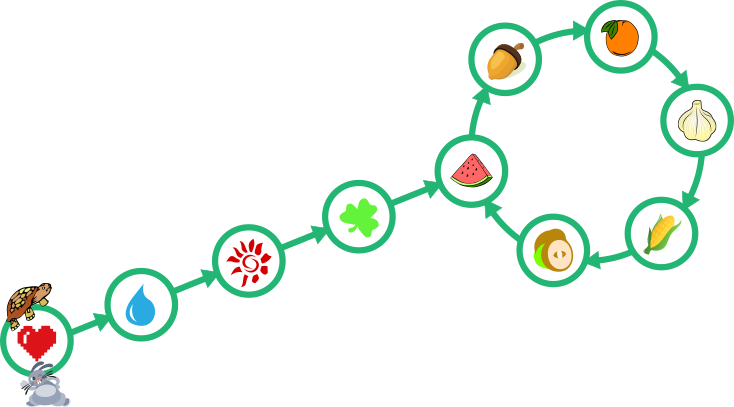
Mõlemad alustavad samal ajal südamega tähistatud väljal ja järgivad rajal olevad nooli. Kilpkonn liigub minutis edasi ühe välja, jänes aga kaks välja.
Millisel väljal nad järgmisel korral kohtuvad?
[Raadionupud]
A. 
B. 
C. 
D. 
E. 
F. 
G. Kilpkonn ja jänes ei kohtu kunagi
Õige vastus on: C.
Alltoodud joonistel on näidatud kilpkonna ja jänese asukohad iga minuti järel.
Pärast 1 minutit:
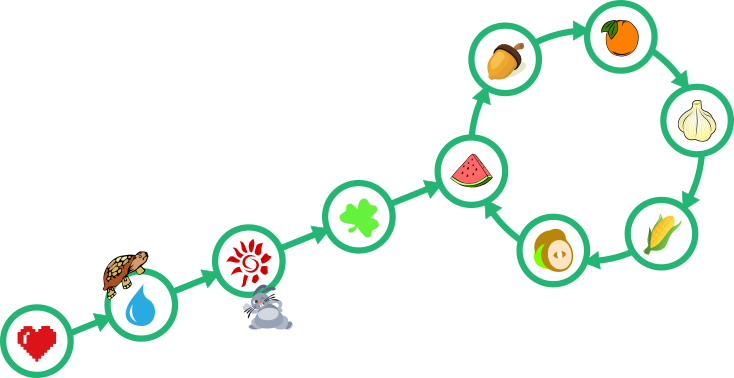
Pärast 2 minutit:
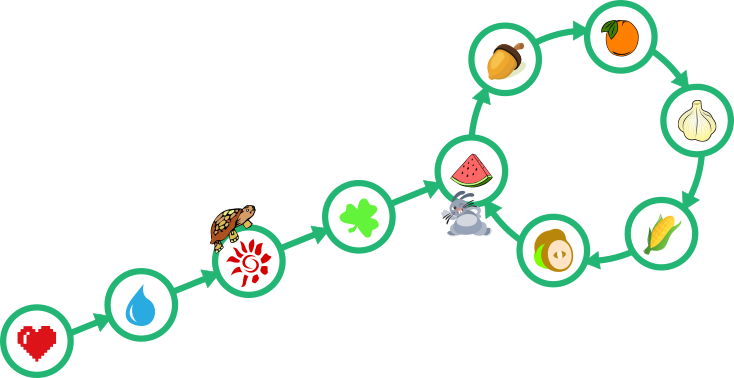
Pärast 3 minutit:
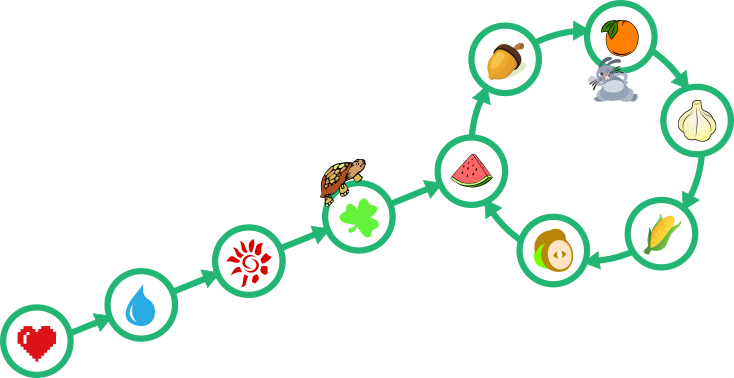
Pärast 4 minutit:
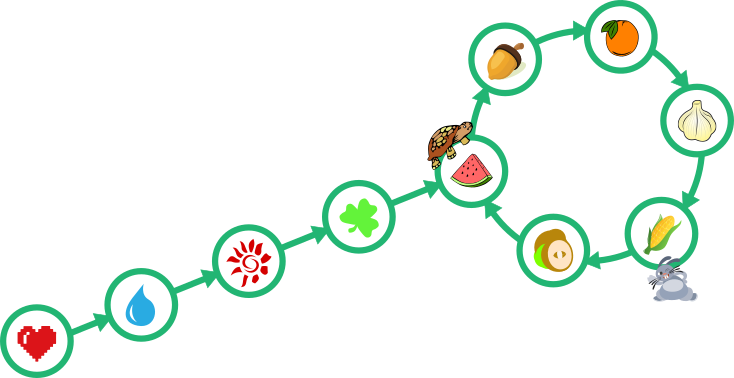
Pärast 5 minutit:
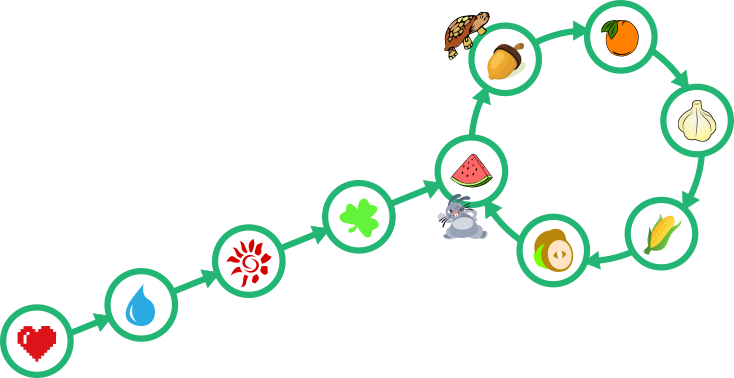
Pärast 6 minutit:
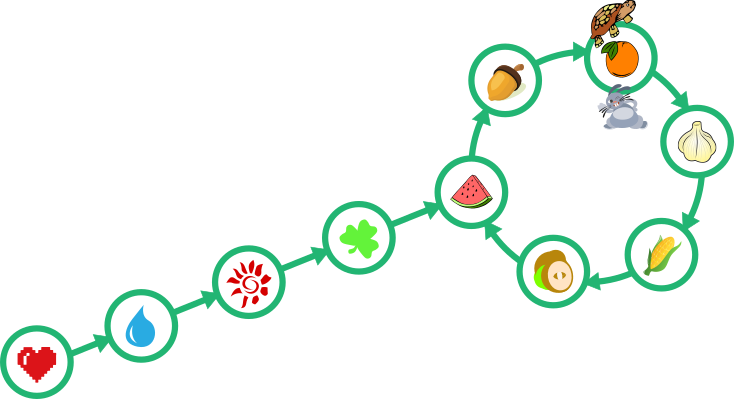
Ülesanne käsitleb ühe teatud andmestruktuuri, nimelt suunatud tsüklitega graafi, läbimist.
Lihtahelat (ingl linked list) kasutatakse selliste andmete säilitamiseks, mis peavad olema omavahel järjendina seotud. Sellise ahela elemente nimetatakse tippudeks; nendeks võivad olla valmistamissammud retseptis, teekonnal läbitavad maamärgid või isegi algoritmi lahendussammud. Sellisel moel salvestatud andmete puhul teavad kõik tipud järgmise tipu aadressi ehk formaalselt väljendudes: igal tipul on olemas viit järgmisele tipule. Tavaliselt on lihtahel lineaarne: kui me alustame esimesest tipust ja järgime viitasid, jõuame me lõpuni, ilma et külastaksime ühtegi tippu mitu korda.
Kui juhtub, et külastame mõnda tippu teist korda, satume me tsüklisse. Kuidas arvutid tsükli olemasolu ära tunnevad? Üks võimalustest, mille pakkus välja Ameerika informaatik Robert W Floyd, on kilpkonna ja jänese algoritm, mis viitab Vana-Kreeka filosoofi Aisopose valmile. Nagu selles ülesandes näha, pannakse kaks punkti liikuma mööda ahelat erineva kiirusega: üks liigub kaks korda kiiremini kui teine. Kui nad kohtuvad, on ahelas tsükkel, vastasel juhul on ahel aga lineaarne.
Tsüklite tuvastamine on informaatikas oluline ülesanne. Nii saab kontrollida, kas meie poolt kirjutatud programmikoodi töö jääb korduma ning seega ei saa programm oma tööd lõpetada. Keerulisemate näidetena võib tuua juhuslike arvude generaatori kvaliteedianalüüsi, et tagada tundlike andmete turvaline krüpteerimine. Enamasti koosnevad sellised algoritmid tsüklieelsest lineaarsest osast ja tsüklist. Mida pikem on tsükkel, seda tugevam on krüpteerimisalgoritm ning seda raskem on seda võõrastel lahti murda.

Kopra Äripank (KÄP) vajab uut valvesüsteemi, et kaitsta oma seifi ees olevat ruumi sissetungijate eest. Nad ostsid viis detektorit. Iga detektor saadab välja kaheksa laserkiirt:

Kui detektori kiir tabab seina, ei juhtu midagi. Kui aga kiire ette jääb sissetungija, aktiveerub häiresignaal. Häire aktiveerub ka siis, kui mõne detektori kiirele jääb ette mõni teine detektor.
KÄP soovib paigutada viis andurit ruudukujulistele põrandaplaatidele nii, et need kataksid kõik ülejäänud plaadid, kuid ei aktiveeriks üksteist. Turvafirma pakub selleks välja neli erinevat skeemi.
Milline pakutud skeemidest ei vasta antud tingimustele?
[Raadionupud]
A. 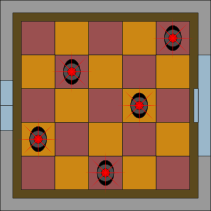
B. 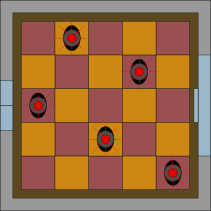
C. 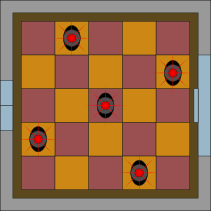
D. 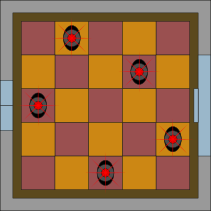
Õige vastus on: D.
Kõiki tingimusi rahuldava lahenduse puhul võib esmalt märgata, et igasse ritta ja igasse veergu paigutatakse parajasti üks detektor, kuna detektorid saadavad välja horisontaalseid ja vertikaalseid kiiri ega tohi üksteist tuvastada. Sellest piisab sissetungija avastamiseks. Tegelikult saadavad detektorid kiiri välja ka diagonaalis, seega tuleb jälgida, et kahte detektorit ei asetataks ka samale diagonaalile.
Kõik need tingimused kehtivad vastuste A, B ja C puhul. Vastuse D puhul põhjustavad kaks detektorite paari häire, kuna need on paigutatud samadele diagonaalidele:
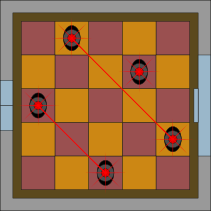
Käsitletav ülesanne on maleülesannetest tuntud kaheksa lipu probleemi variatsioon. Arvutiteaduse seisukohast on see kitsenduste rahuldamise probleemi (ingl Constraint Satisfaction Problem, CSP) näide. Meil on objektid (meie ülesandes detektorid), millel võivad olla erinevad väärtused (meie ülesandes asukohad) ja iga objekti jaoks peab valima ühe võimalikest väärtustest sellisel viisil, et ei rikutaks etteantud reegleid. Sellised probleemid tekivad sageli näiteks robotite töö planeerimisel, arvutilingvistikas keeletuvastuse puhul või ressursside jagamisel. Sellised ülesanded võivad muutuda väga kiiresti keeruliseks, nii et nende lahendamiseks on vaja arvutit. Arvutid lähenevad probleemile samamoodi, nagu me ise teeme: nad püüavad lahenduseni jõuda sammhaaval. Niipea, kui mõnda reeglit rikutakse, võtavad nad ühe või mitu sammu tagasi ja proovivad seejärel järgmist võimalust, kuni leiavad lahenduse, mis sobib kõikidele piirangutega.
Kuidas aga arvuti otsustab, kas kaks detektorit üksteist häirivad või mitte? See on juba arvutusgeomeetria valdkonna ülesanne. Nummerdame põrandaplaatide read ülalt alla ja veerud vasakult paremale. Olgu ühe detektori rea- ja veerunumber a ja b ning teise omad vastavalt c ja d. Siis

Bambu on restoran, mis pakub eksootilisi rahvusroogi. Restoranis on kaks kokka. Kumbki kokk saab korraga tegeleda ainult ühe roaga. Nad valmistavad roogi alati vastavalt tellimise järjekorrale. Kuna igal roal on erinev valmistusaeg, ei pruugi esimesena tellitud roog esimesena kliendile lauale jõuda.
Roogade valmistusajad (koos serveerimisega) on järgmised:
| Roog | Nimi | Valmistusaeg |
|---|---|---|
 |
Praetud riis | 5 minutit |
 |
Satay kana | 14 minutit |
 |
Härjasabasupp | 7 minutit |
Ühel päeval sisenes restorani 5 inimest ja ettekandja sisestas nende tellimused sellise järjekorras:
Milline oli toitude serveerimise järjekord?
[Raadionupud]
A. 1-2-3-4-5
B. 1-3-2-5-4
C. 3-4-1-5-2
D. 1-3-2-4-5
E. 1-4-3-2-5
Õige vastus on: D.
Kui me simuleerime tellimuse järjestust ja asetame need ajajoonele kuni kõigi tellimuste serveerimiseni, saame järgmise tabeli:

Kui me järjestame selle nimekirja serveerimisaja järgi, saame me vastuseks 1-3-2-4-5.
Restorani töökorraldus sarnaneb klient-server arhitektuuriga. Klient saadab serverile päringu, seejärel server vastab ja tagastab nõutud andmed. Serveri reageerimisaeg sõltub paljudest teguritest, näiteks failitüüp, faili suurus, ühenduse kiirus, ummikud jne. Seega ei jõua esimese päringu vastus alati esimesena kliendini. Samuti on igal serveril operatsioonisüsteemi poolt juhitavad töölõimed, mis piiravad samaaegselt töödeldavate päringute arvu.

Jaanika istutas peenrale vasakult paremale seitse lille. Ta valis lilli vastavalt järgmistele reeglitele:
Kõige vasakpoolsemasse auku võib ta istutada suvalise lille.
Igasse järgmisse auku võib istutada ainult sellise lille, mille puhul on alloleval skeemil nool eelmisena istutatud lille juurest järgmisena istutatava lille juurde.

Näiteks võib Jaanika istutada tulbi ja selle kõrvale nartsissi, kuna skeemil on nool tulbi juurest nartsissi juurde. Vastupidine variant pole lubatud, kuna nartsissist tulbini viivat noolt ei ole.
Milline järgnevatest peenardest pole loodud vastavalt Jaanika reeglitele?
[Raadionupud]
A. 
B. 
C. 
D. 
Õige vastus on: D.
Nummerdame nooled Jaanika skeemil selliselt:

Peenra A saab istutada, alustades tulbist ja liikudes mööda nooli 1, 3, 4, 2, 7 ja 7.
Peenra B saab istutada, alustades nartsissist ja liikudes mööda nooli 3, 4, 3, 5, 1 ja 3.
Peenra C saab istutada, alustades tulbist ja liikudes mööda nooli 1, 3, 5, 1, 2 ja 7.
Peenra D puhul võime alustada lumikellukesest ja liikuda edasi mööda nooli 4 ja 2. Aga kannikesest tulbini noolt pole ja seepärast seda peenart reeglipäraselt lõpetada ei saa.

Veelgi enam: kui Jaanika istutab kasvõi ühe kannikese, peab ta kõik järgmised istutusaugud kannikestega täitma, sest skeemil ei lähe noolt kannikese juurest ühegi teise lille juurde.
Jaanika plaan meenutab arvutiteadusest tuntud olekumasinaid (ingl state machine). Selline masin on alati mingis olekus ja masina kirjeldus määrab, millistesse teistesse olekutesse igast olekust edasi liikuda võib. Jaanika reeglite kohaselt on viimasena istutatud lill peenra olek. Kuna tema skeem kirjeldab, milliseid lilli tohib iga lille järele istutada, määrabki see lubatud üleminekud olekute vahel.
Selliseid olekumasinaid (mõned lihtsamate, mõned keerulisemate reeglitega) kasutatakse arvutiteaduses sageli. Üks levinud rakendus on sisestatud andmete korrektsuse kontrollimine. Näiteks võib tabelarvutusprogramm kasutada olekumasinat, et kontrollida, kas kasutaja sisestatud tekst on arv või korrektne valem.
Teine näide on e-posti aadressi vormi kontroll: kas selles on olemas @-märk, ega kasutajanimes või domeeninimes pole lubamatuid märke, jne. Samas tasub tähele panna, et olekumasinaga saab kontrollida ainult aadressi vormilist korrektsust. Seda, kas aadress ka päriselt olemas on, tuleb küsida selle domeeni meiliserverilt.

Mari leidis aardelaeka, kuid see on lukus. Avamiseks on vaja õiget kombinatsiooni kolmest kujundist. Aita Maril laegas avada, kui on antud järgmised kombinatsioonid koos kommentaaridega.


 Üks kujund on õige ja õiges kohas.
Üks kujund on õige ja õiges kohas.

 Ükski kujund pole õige.
Ükski kujund pole õige.

 Kaks kujundit on õiged, kuid paiknevad vales kohas.
Kaks kujundit on õiged, kuid paiknevad vales kohas.

 Üks kujund on õige, kuid vales kohas.
Üks kujund on õige, kuid vales kohas.

 Üks kujund on õige, kuid vales kohas.
Üks kujund on õige, kuid vales kohas.Milline järgmistest kombinatsioonidest avab aardelaeka?
[Raadionupud]
A. 


B. 


C. 


D. 


Õige vastus on: B.
Üks võimalus selle ülesande lahendamiseks on antud variantide sobivust ükshaaval kontrollida.
Variandid A, C ja D ei saa õiged olla: kolmandas vihjes on öeldud, et selles on kaks õiget kujundit, aga kumbki pole oma õiges kohas; neis kolmes variandis on aga kõigis täht samas kohas kui vihjes.
Variant B on ainsana kooskõlas kõigi vihjetega:
Teine võimalus (huvitavam, aga ka veidi keerulisem) on variante mitte vaadata ja koostada lahendus vihjete põhjal.
Alustame nende kujundite välistamisest, mis kindlasti kombinatsiooni ei sobi. Teises vihjes on öeldud, et ükski antud kujunditest ei kuulu õigesse kombinatsiooni, see tähendab, et meie vastuses ei tohi olla ei kuuske, rombi ega noolt.
Viimases vihjes on kirjas, et üks kujund on õige, kuid vales kohas. Kuna meil on juba teada, et kuuske ja noolt ei kasutata, tähendab see seda, et õige kujund peab olema täht, kuid see on paigutatud valesse kohta. Seega on tähe võimalikke asukohti kaks:


 või
või 


Kolmas vihje ütleb, et kaks kujundit sobivad, kuid asuvad vales kohas. Üks neist on kindlasti täht, kuid nüüd selgub, et see ei saa asetseda keskel, seega saame kindlalt paika panna tähe asukoha:



Nii leidsime üles ühe kujundi ja selle õige asukoha.
Edasi püüame leida ülejäänud kaks kujundit. Esimesest vihjest näeme, et üks antud kujunditest on õige ja ka sobivas kohas. Selleks ei saa olla nool, kuna noolt võimalike kujundite hulgas ei ole, seega peab olema õige üks järgmistest variantidest:


 või
või 


Kuna juba teame, et esimeses ruudus on täht, ei saa seal olla kolmnurk. Järelikult on just kuu see, mis asub õigel positsioonil. Seega:



Neljandast vihjest selgub, et üks kujund on õige, aga vales kohas. Kolmnurk läheks vastuollu esimese vihjega. Ka süda ei sobi: ainus vaba koht on keskmine, aga süda on keskel ka vihjes ja seega poleks vales kohas. Järelikult peab keskmiseks kujundiks olema ring:



Mõttekäik ülesande lahendamisel võib olla ka teistsugune, kuid kõik viivad tulemuseni, et õige vastus on B.
Informaatikas on mustrituvastuse eesmärgiks on kontrollida, kas mingi jada elementidest vastab etteantud mustrile. Antud ülesande puhul jälgisime vihjeid ja koostasime mustri, mis avaks aardelaeka. Tavaelus kontrollitakse mustrituvastusega näiteks sõnade õigekirja.

Alara on türgi vaibakuduja. Ta valmistab vaipu, millel on ruudukujuline muster suurusega 6 korda 6 ruutu.
Alara paigutab kujundeid ruutudesse vastavalt järgmisele plaanile:
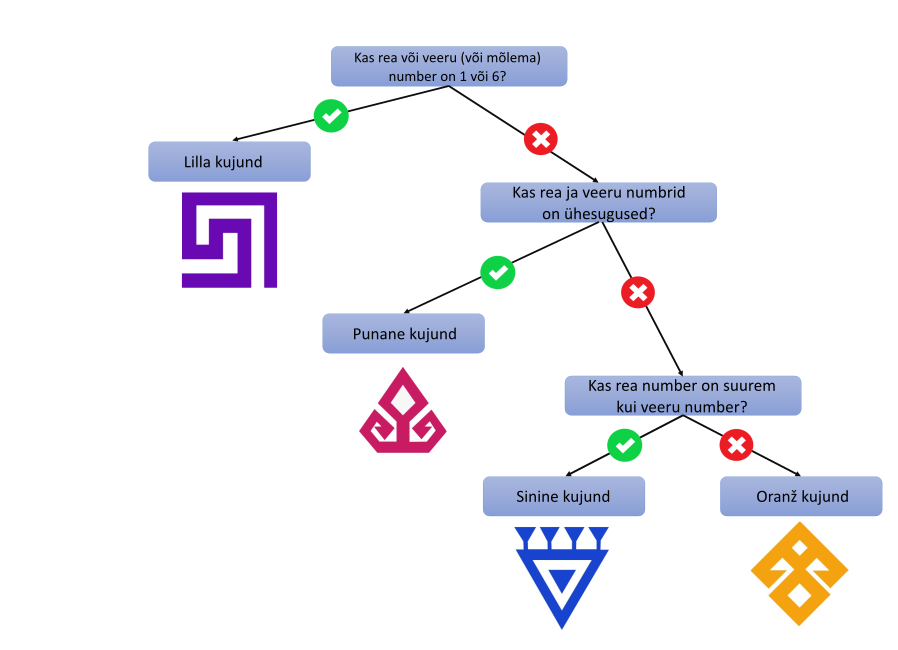
Milline näeb välja sellise plaani alusel kootud vaip?
[Raadionupud]
A. 
B. 
C. 
D. 
Õige vastus on: B.
Esimene juhis näitab, et nii esimeses ja kuuendas reas kui ka esimeses ja kuuendas veerus on lillad kujundid:
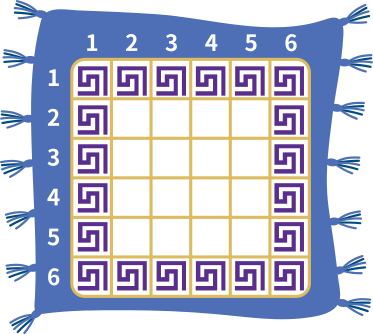
Teine juhis viitab sellele, et kõik senised tühjad ruudud diagonaalil, mis algab vasakult ülevalt nurgast, on täidetud punaste kujunditega, kuna nende puhul on rea ja veeru numbrid samasugused:
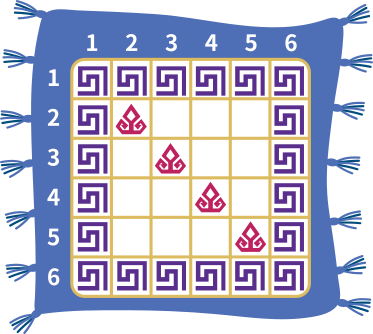
Kolmanda juhise puhul näeme, et rea number on veeru numbrist suurem diagonaalist vasakul asuvatel ruutudel, seega paneme neisse sinised kujundid:
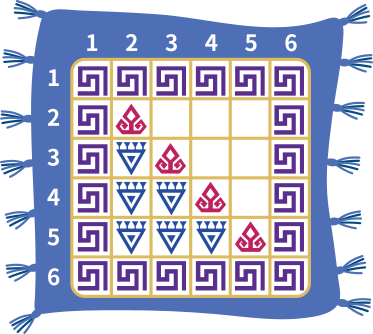
Ülejäänud tühjade ruutude puhul pole rea number suurem kui veeru number, seega täidame need oranžide kujunditega. Nii saamegi vaiba, mida on kujutatud variandi B all.
Matemaatikas ja informaatikas tähendab algoritm defineeritud sammude lõplikku jada, tüüpiliselt kasutatakse seda mingite sarnaste probleemide lahendamiseks.
Otsustuspuu (ingl decision tree) on üks võimalus visualiseerida lihtsa tingimuslausetest koostatud algoritmi struktuuri. See tähendab, et iga tase selles puus koosneb küsimusest või väitest: kui vastus sellele küsimusele on "jah" (või väide on tõene), jätkatakse ühe, vastasel juhul aga teise haruga. Nii liigutakse erinevate harude kaudu, kuni jõutakse väljundini.
Tasub ka tähele panna, et sageli on oluline tingimuste kontrollimise järjekord. Näiteks kui me selle ülesande otsustuspuus vahetakse kahe esimese tingimuse järjekorra, oleks tulemuseks vaip C.

Koprad soovivad meisterdada endale tavalist jalgpalli.

Nad leidsid kasutamiseks neli erinevat nahatükki.
Millisest neist tükkidest saab teha ülaltoodud pildil oleva jalgpalli?
[Raadionupud]
A. 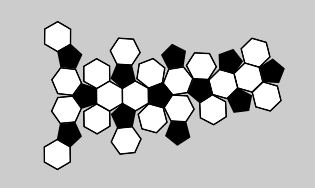
B. 
C. 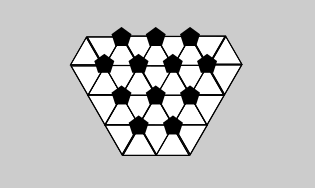
D. 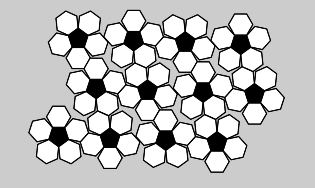
Õige vastus on: A.
Kui vaadata palli, siis näeme, et kõik valged kujundid on kuusnurksed, mustad aga viisnurksed. Seega võime eemaldada variandid B (milles olevad mustad kujundid on hoopis kuusnurgad) ja C (kus kasutatakse hoopis valgeid kolmnurki kuusnurkade asemel).
Samuti näeme, et igal kahe musta viisnurkse kujundi vahel on vaid üks kuusnurga serv. Seega ei sobi ka variant D, kuna seal on kaks musta viisnurkset kujundit eraldatud teineteisest vähemalt kahe kuusnurgaga.
Järele jääb ainult variant A.
Paneme tähele, et mustrite A ja D tükid ei ole joonisel täielikult omavahel ühendatud, kuna tegemist on kolmemõõtmelise pinna kujutamisega kahemõõtmelisena. Kõik sobib ideaalselt, kui kujundid välja lõigata ja kokku voltida.
Mustrituvastus on üks informaatika nurgakivisid. Ülesandest korduvate mustrite leidmine lihtsustab selle lahendamist olulisel määral. Mustrituvastuse abil leitakse ka objektide sarnasusi ja erinevusi, see on lähedane inimese tajule. Näiteks tunneb inimene ära kassi vastavalt kassile iseloomulikele omadustele. Ka arvuti tuvastab kassile omaste tunnuste abil, kas tegemist on kassipildiga.
Mustrituvastus aitab inimesi erinevatel elualadel. Näiteks tervishoius kasutatakse seda haiguste diagnoosimisel, haigestumisriski ennustamisel jne, põllumajanduses aga leitakse taimehaigusi lehtedest tehtud piltide järgi.

Järgnevas tekstilõigus on tühikud tähistatud märgiga '·' ja lõiguvahetused märgiga '¶'. Tähistamata reavahetused on tekstitöötlusprogrammi poolt automaatselt lisatud.
§·1.·Eesti·on·iseseisev·ja·sõltumatu·demokraatlik·vabariik·,kus·kõrgeima·
riigivõimu·kandja·on·rahvas.·Eesti·iseseisvus·ja·sõltumatus·on·aegumatu·
ning·võõrandamatu.¶
§·2.·Eesti·riigi·maa-ala,territoriaalveed·ja·õhuruum·on·lahutamatu·ja·
jagamatu·tervik·.·Eesti·on·riiklikult·korralduselt·ühtne·riik,·mille·
territooriumi·haldusjaotuse·sätestab·seadus.¶Mitmes sõnavahes on selle teksti vormistamisel tühikuid valesti kasutatud?
(Kui ühes sõnavahes on mitu viga, lugeda seda ainult üks kord.)
[Täisarv]
Õige vastus on: 3.
Esimene viga on 'vabariik·,kus', kus tühik peaks olema koma järel, mitte selle ees.
Teine viga on 'maa-ala,territoriaalveed', kus peaks koma järel olema tühik.
Kolmas viga on 'tervik·.·Eesti', kus punkti ees ei peaks tühikut olema.
Lisaks sellele, et kirjavahemärkide valesti kasutamine on eksimine õigekirjareeglite vastu, võib see tekstide arvutis töötlemisel kaasa tuua ka ebameeldivusi automaatse reapoolitusega. Kui jätta koma või punkti järele tühik panemata, ei saa tekstitöötlusprogramm sellesse kohta vajadusel reavahetust lisada; sellega võib kannatada teksti joondamine. Kui panna tühik koma või punkti ette, võib tekstitöötlusprogramm sinna automaatse reavahetuse lisada ja nii satub kirjavahemärk üksikuna järgmise rea algusse; ka see näeb inetu välja.
Õigekirja seisukohalt võib arutada, kas 'vabariik·,kus' on üks viga (tühik ja koma on omavahel vales järjekorras) või kaks viga (koma ees liigne tühik, koma järel vajalik tühik puudu). Selleks, et oleks üheselt selge, ongi ülesandes küsitud vigade arvu asemel nende sõnavahede arvu, kus on midagi valesti. Samasugust täpsust on vaja paljudes olukordades, kus erinevad osapooled (olgu inimesed või arvutid) peavad mingit reeglit kõik ühtemoodi mõistma — näiteks siis, kui eesti keele eksami etteütluse osas on hindamine määratud vigade arvuga.

Vaatame järgmist tabelarvutuse töölehte, mille mõnes lahtris on arvud ja mõnes valemid:
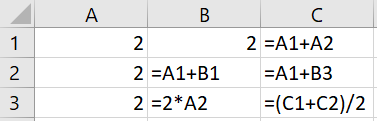
Milline väärtus tuleb tabeli lahtrisse C3?
[Täisarv]
Õige vastus on: 5.
Lahtri C3 arvutamiseks on vaja lahtrite C1 ja C2 väärtusi. C1 arvutamiseks on kõik andmed olemas, sinna tuleb 2+2=4. C2 arvutamiseks on vaja B3 väärtust. B3 väärtuseks saame 2*2=4, seejärel C2 väärtuseks 2+4=6 ja lõpuks C3 väärtuseks (4+6)/2=5.
Lahtri B2 väärtust meil vaja ei läinud ja selle võisime arvutamata jätta.
Tabelarvutuse töölehtede valemid võimaldavad korduvaid arvutusi automatiseerida ning sellega kasutajate aega kokku hoida ja käsitsi arvutamisest tulenevate vigade arvu vähendada.

Kalle ja Kati Kobras õpivad tekstipõhise kasutajaliidese ehk nn "käsurea" kasutamist enda arvutis.
Kalle vaatab faile enda arvutis nii käsurealt kui ka graafilises vaates:
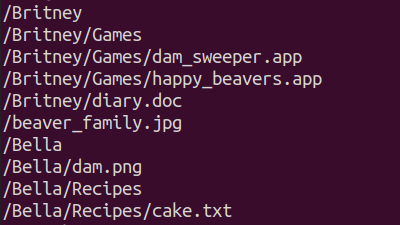
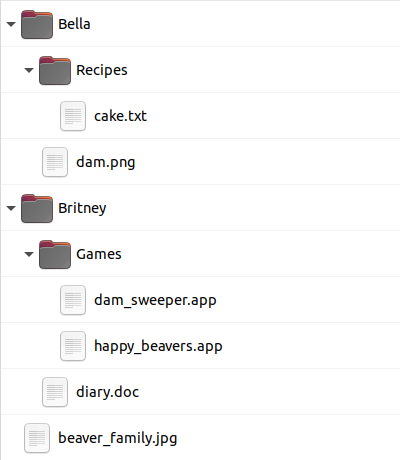
Kati vaatab faile enda arvutis ainult käsurea abil:
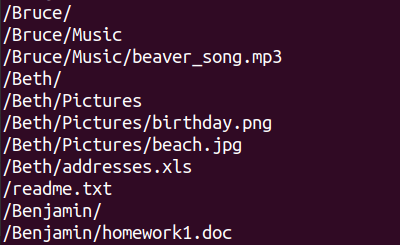
Milline alltoodutest vastab Kati arvuti failide graafilisele vaatele?
[Raadionupud]
A. 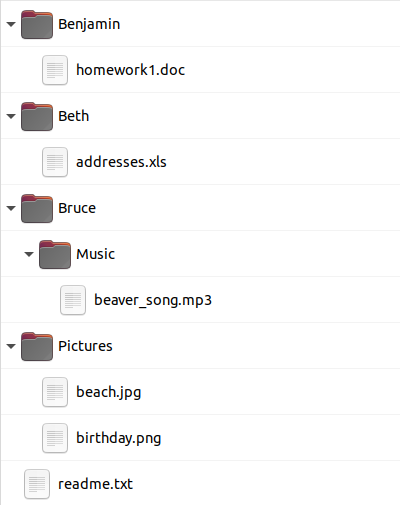 B.
B. 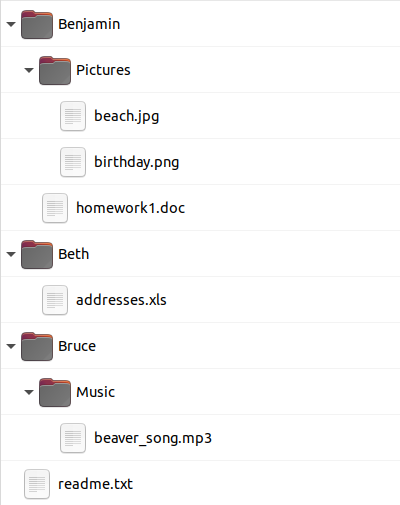 C.
C. 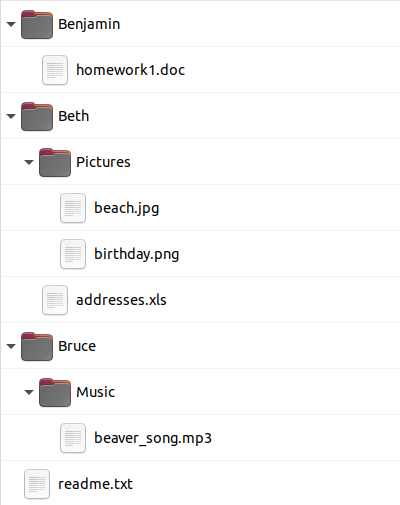 D.
D. 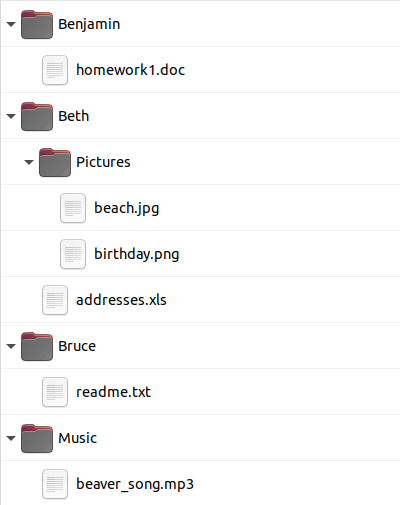
Õige vastus on: C.
Variandid A ja B näitavad kausta "Pictures" vales kohas, D puhul on vales kohas aga kaust "Music" ja fail "readme.txt".
Arvutis hoitakse faile hierarhilises struktuuris. Selles on olemas failid ja kaustad, iga fail asub ühes kaustas ja (kui välja arvata kõige üldisem ehk juurkaust) ka iga kaust asub ühes kaustas. Muidugi võib igas kaustas olla mitu faili ja kausta. Sellise süsteemi idee on väga vana, samasugust põhimõtet kasutati paberdokumentide hoidmiseks juba enne arvutite leiutamist. Selline struktuur annab võimaluse ka paremaks õiguste haldamiseks: juurdepääsu võib anda ühele kaustale koos selle sees olevate kaustadega.
Tänapäeval kasutatakse ka teistsuguseid süsteeme, näiteks meilid on sageli nö "märgendatud" (ingl tagged) ja ühel meilisõnumil võib olla mitu erinevat märgendit.
Failistruktuur on üks näide puustruktuurist, mis on väga tavaline viis hierarhilise info organiseerimiseks ja säilitamiseks paljudes programmides.

Ahelkood on kokkuhoidlik viis must-valgel pildil olevate kontuuride (piirjoonte) esitamiseks. Põhimõte on valida üks must piksel ja salvestada igal sammul suund liikumiseks järgmise musta pikslini kontuuri päripäeva (kellaosuti liikumise suunas) läbimisel.
Suunad on tähistatud numbritega selliselt:
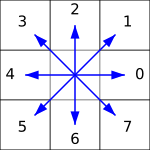
Näiteks kui valime alloleval pildil esimeseks sinise raamiga tähistatud piksli, saame edasi liikuda punaste nooltega näidatud suundades ja tulemuseks on ahelkood 1, 0, 0, 7, 7, 5, 5, 4, 3, 3, 2.
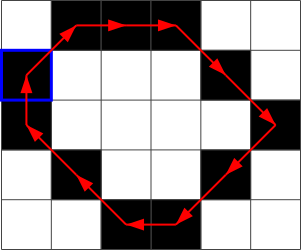
Vaatame nüüd sellist pilti:

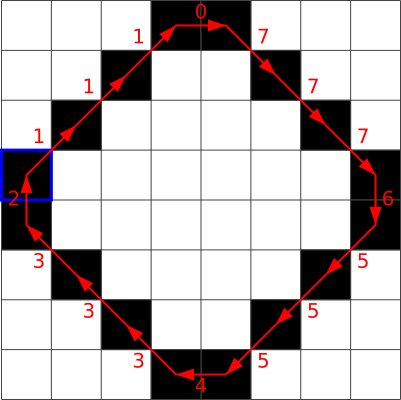
Milline järgmistest on selle pildi ahelkood?
[Raadionupud]
A. 1, 1, 1, 0, 7, 7, 7, 6, 5, 5, 5, 4, 3, 3, 3, 2
B. 1, 1, 0, 0, 7, 7, 6, 6, 5, 5, 4, 4, 3, 3, 2, 2
C. 6, 7, 7, 7, 0, 1, 1, 1, 2, 3, 3, 3, 4, 5, 5, 5
D. 0, 1, 1, 0, 7, 7, 7, 6, 5, 5, 5, 4, 3, 3, 3, 0
Õige vastus on: A.
Ahelkood on üks meetod objektide esitamiseks nende kontuuride abil. Ahelkood on määratud stardipiksli määramisega ja suunavektorite jadaga vastavalt sellele, kas igal sammul suundutakse kontuuri järgmise musta pikslini vasakul, paremal, üleval, all või diagonaalis. Ahelkoodi eeliseks on vajaliku info säilitamine ja samas andmemahu väga suur kokkuhoid. Esimesena esitles ahelkoodi ideed Freeman 1961. aastal ning seepärast on see tuntud ka kui Freemani ahelkood (ingl Freeman Chain Code, FCC).
Ahelkoodi üks kasutusala on numbrituvastus. Esiteks võimaldab see kood objekte kompaktselt esitada, teiseks on ahelkoodide võrdlemine lihtsam kui piltide võrdlemine. Lisaks sellele on ahelkoodist võimalik välja lugeda ka kujutatava objekti üksikuid omadusi. Ahelkoodid esindavad kadudeta tihendamist ja säilitavad kogu info, mis on vajalik kiireks ja efektiivseks mustrite analüüsiks.

Tanel seisis kaheksast puust ümbritsetud lagendikul sees ja tegi puudest 360-kraadise foto.

Mõne päeva pärast tuli Tanel samasse kohta tagasi ja nägi, et kaks puud oli vahepeal maha saetud. Ta tegi sarnase foto, aga alustas oma 360-kraadist ringi esimese korraga võrreldes teisest suunast.
Millise foto allolevatest tegi Tanel teisel korral?
[Raadionupud]
A. 
B. 
C. 
D. 
Õige vastus on: C.
Kui me nummerdame esimesel fotol olevad puud, siis saame sellise pildi:

Kui me muudaksime natuke vaatenurka ja teeksime uue foto, saaksime pildi, kus puud oleksid küll samas järjekorras, aga nihkes. Ka nüüd nummerdame fotol olevad puud, aga nii, et mõlemal fotol vastavad samad numbrid samadele puudele.

Nüüd kontrollime, kas kõik puud allolevatel fotodel on nummerdatud samal viisil ja on õiges järjekorras.
Variandi A puhul on maha lõigatud puud numbritega 1 ja 5, kuid puu numbriga 4 on teistsuguse kujuga kui esimesel pildil.

Pildil B on maha saetud puud numbritega 6 ja 3, kuid puu numbriga 1 on erineva kujuga võrreldes esimese pildiga.

Kui me võrdleme varianti C, näeme, et puud 4 ja 3 on maha saetud ja ülejäänud on õiges järjekorras.

Variandi D puhul on langetatud puud numbritega 1 ja 6, kuid siin on nii 4. kui 5. puu erineva kujuga.
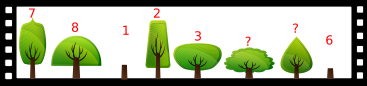
Ülesande lahendamiseks on vaja leida puude järjekorda iseloomustav muster ja proovida seda vastusevariantide peal. Oskus tuvastada mustreid lubab meil leida vigu jadas. Momendil on oluline leida puude järjekord. Kui katsetame saadud mustrit erinevate variantide peal ja leiame selles erinevuse, nimetame me seda veaks. Seda protsessi nimetatakse vigade tuvastamiseks, millel on tähtis osa programmide testimisel. Kui osa infost puudub (nagu antud näites oli osa puid maha saetud), on vigade tuvastamine keerulisem.
Copyright © 2022 Bebras – International Challenge on Informatics and Computational Thinking.
Licensed under Creative Commons Attribution-ShareAlike 4.0 International License.
Flag icons by GoSquared.