

Бобрик работает на конвейере металлообрабатывающего завода, который производит гайки и болты.

Его работу можно описать следующим образом:
У Бобрика могут возникнуть проблемы двух типов:
Какая из следующих последовательностей гаек  и болтов
и болтов  на конвейере не приведёт к проблемам в работе Бобрика (последовательность следует читать слева направо)?
на конвейере не приведёт к проблемам в работе Бобрика (последовательность следует читать слева направо)?
[Raadionupud]
A. 
B. 
C. 
D. 
Правильный ответ: C.
В варианте С мы можем проследить состояния корзины и конвейера с помощью таблицы, где Г обозначает гайку  , а Б — болт
, а Б — болт  :
:
| Корзина | Конвейер |
|---|---|
| пустая | Г Б Г Г Б Г Г Б Б Б |
| Г | Б Г Г Б Г Г Б Б Б |
| пустая | Г Г Б Г Г Б Б Б |
| Г | Г Б Г Г Б Б Б |
| Г Г | Б Г Г Б Б Б |
| Г | Г Г Б Б Б |
| Г Г | Г Б Б Б |
| Г Г Г | Б Б Б |
| Г Г | Б Б |
| Г | Б |
| пустая | пустая |
В варианте А проблема возникнет после последовательности "Г Б Б", потому что в момент получения второго болта в корзине не будет ни одной гайки.
В варианте B проблема возникнет после последовательности "Г Г Б Г Г Б Б Б Б", потому что в момент получения пятого болта в корзине не останется ни одной гайки (до этого момента с конвейера Бобрик получил только 4 гайки).
В варианте D проблема возникнет после прохождения целого ряда, потому что с конвейера пришло 6 гаек и 4 болта. Следовательно, 2 гайки останутся неиспользованными.
Данное задание — это пример так называемого автомата с магазинной памятью (англ push-down automaton, PDA). Этот автомат является одной из возможностей описать алгоритм, который основывается на состояниях и имеет неограниченный объём памяти в виде так называемого стека (англ stack). В случае стека действует правило: в него последним добавленный элемент извлекается первым. В данном случае состояние задаётся тем, что именно придёт с конвейера следующим — гайка или болт; а стек представлен в виде корзины для хранения гаек.
Автомат с магазинной памятью применяется, например, для распознавания и анализа контекстно-свободных языков. Помимо прочего, анализ языка означает выяснение является ли данная последовательность символов подходящей для данного языка, то есть принадлежит ли она данному языку. В данном задании мы можем представить гайки и болты как скобки и их уравновешивание, где Г будет открывающейся скобкой ("("), а Б — закрывающей скобкой (")"). Равновесие скобок означает порядок, соответствующий правилам скобок в арифметических выражениях. Например, в последовательностях "(((()" и "())(" скобки не уравновешены. Распознавание равновесия скобок очень важно для компилятора, потому что некоторые языки программирования используют скобки не только для арифметических выражений, но и для разметки структуры программы.

У Вити есть шестиугольные кусочки пазла трёх разных цветов. Если он выложит три кусочка рядом друг с другом в форме треугольника (как показано на нижеприведённом рисунке), то все эти кусочки должны быть либо одного цвета, либо разного.
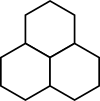
Витя решил выложить из кусочков пазла башню. Сначала он выложил нижний ряд, как показано на нижеприведённом рисунке.
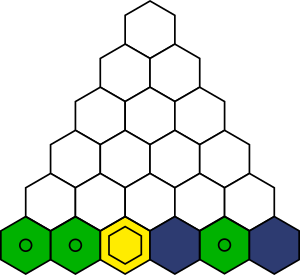
Какого цвета будет самый верхний кусочек башни, если во время построения башни Витя всегда будет следовать правилу треугольника?
[Raadionupud]
A. 
B. 
C. 
D. Существует больше одной возможности
Правильный ответ: B.
Если мы знаем цвета двух расположенных рядом друг с другом шестиугольников, то они определяют то, какого цвета будет расположенный над ними кусочек. Например, возьмём расположенные внизу с левой стороны кусочек, цвет которого мы ещё не знаем. Так как расположенные под ним два шестиугольника являются зелёными, то и этот кусочек должен быть зелёным. Посмотрев далее на кусочек, которые расположен чуть правее от уже рассмотренного, мы поймём, что он должен быть синего цвета (ведь один из расположенных под ним кусочков является зелёным, а другой — жёлтым).
Используя эту идею, мы можем двигаться к вершине башни, и результат будет следующим:
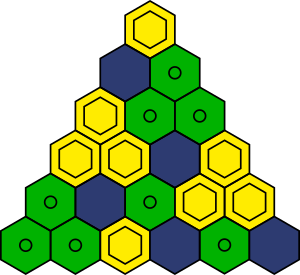
Обратите внимание, что к такому же результату мы придём не зависимо от того, с какого конца мы будем анализировать каждый ряд.
Мы выяснили, что выбор одного из двух правил зависит от того, какого цвета будут два нижерасположенных шестиугольника — одинакового или разного. Мы должны повторять свои действия до тех пор, пока нам не станут известны цвета всех кусочков башни. Такая последовательность шагов образует алгоритм, который мы и используем для решения этого задания. Если бы мы написали аналогичную программу, то выбор между двумя правилами соответствовал бы условному предложению, а выполнение этого выбора для каждого следующего кусочка был бы повторяющимся предложением.
Составление алгоритмов и их реализация в виде программ является одной из центральных и наиважнейших задач информатики. Для этого необходимо найти не только шаблон-паттерн, то и логику для деления задания на части.

Каждый год на склоне Бобровой горы проходит соревнование по горному слалому. В нём принимает участие и Марта, которая в этом году планирует выиграть. В списках участников Марта заявлена под последним номером. Чтобы выиграть соревнование, время её спуска должно быть меньше времени, которое показал текущий лидер соревнования.
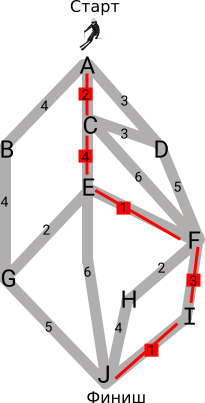
Карта склона Бобровой горы приведена ниже. Чтобы добраться до финиша, участник должен ехать только по трассе вниз, но каждый участник соревнования сам выбирает по каким участкам он будет проходить трассу. Рядом с каждым участком указано количество минут, которое потребуется Марте для его прохождения.
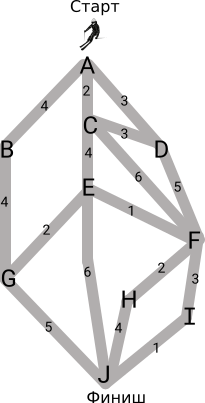
Через какие пункты должна проходить трасса Марты, чтобы выиграть соревнование, если время текущего лидера составляет 12 минут?
(Запиши последовательность букв-пунктов от A до J, через которые пройдёт трасса Марты, без каких-либо дополнительных символов; например, ABGJ.)
[Tekstikast]
Правильный ответ: ACEFIJ.
Для победы в соревновании Марта должна выбрать такую последовательность участков трассы, прохождение которой от старта А до финиша J потребует менее 12 минут. Она должна начать свой спуск из пункта-старта, то есть из пункта А. Из этого пункта выходит 3 участка трассы, которые ведут к пунктам B, C и D и добраться до которых можно за 4, 2 и 3 минуты, соответственно. Рядом с каждым пунктом Марта записывает число, которое показывает самое быстрое время для достижения этого пункта. Далее рассмотрим пункты в порядке времени их достижения.
Теперь от пункта А перейдем к рассмотрению пункта C. Выходящие из пункта С участки ведут к пунктам D, E и F и время, соответственно, будет 3, 4 и 6 минут. (Возвращение к пункту А было бы подъёмом вверх по горе, а это противоречит условиям соревнования.) Значит, для прохождения трассы через пункты A→C→D потребуется в итоге 2+3=5, через пункты A→C→E потребуется 2+4=6, а через пункты A→C→F потребуется 2+6=8 минут. На прошлом этапе решения этого задания мы уже выяснили, что прохождение отрезка A→D займёт 3 минуты, а это явно быстрее, чем прохождение трассы через пункты A→C→D. Значит, записанное около пункта D число остаётся неизменным; около пункта E Марта записывает число 6, а около пункта F — число 8.
Далее перейдём к участкам, которые начинаются из пункта D. Единственным подходящим для рассмотрения пунктом является F, рядом с которым Марта ранее уже записала число 8. Время для прохождения участка A→D→F вновь составляет 8 минут, и поэтому мы ничего менять не будем. Далее обратим внимание на участки, которые начинаются из пункта B — в данном случае есть только один подходящий участок. Время для прохождения трассы A→B→G составляет 8 минут, которое Марта и записывает рядом с пунктом G.
На данный момент Марта уже рассмотрела участки, которые начинаются из пунктов A, B, C и D. Далее рассмотрим пункт E. Чтобы сюда добраться, потребуется 6 минут. Значит, чтобы через пункт Е добраться в пункт G потребуется 6+2=8, в пункт J — 6+6=12, в пункт F — 6+1=7 минут. Достижение пункта G через пункт E или B берёт одинаковое количество времени (8 минут). Прохождение участка A→C→E→F потребует только 7 минут, то есть это будет быстрее, чем ранее найденный отрезок A→D→F. Чтобы через пункт Е добраться в пункт J потребуется 12 минут — однако Марте для победы надо показать время, которое будет лучше этого. Если Марта будет аналогично рассуждать и в случае пункта F, то доберётся до пункта I за 7+3=10 минут, а в пункт H за 7+2=9 минут.
Через пункт G в пункт J Марта доберётся за 8+5=13 минут, а это её не устраивает. Следующий вариант касается рассмотрения трассы, проходящей через пункты H или J. Однако и в этом случае время составило бы 9+4=13 минут. Напоследок рассмотрим участок I→J (то есть вся трасса бы проходила через пункты A→C→E→F→I→J). Мы видим, что в этом случае Марта пройдёт трассу успешно, то есть за 11 минут. Это решение видно и на нижеприведённом рисунке.
Это задание связано с нахождением кратчайшего пути в графе.
В информатике системы, которые состоят из пунктов и соединяющих их отрезков, называются графами. В теории графов задание на нахождение кратчайшего пути означает поиск такого пути между двумя пунктами, то есть вершинами, графа, где сумма пройденных участков пути, то есть сумма весов его рёбер, будет наименьшей возможной.
В данном задании участники соревнования перемещаются с горы вниз и тем самым даётся подсказка, что мы имеем дело с ориентированным графом. Если в каком-нибудь другом задании можно было бы на каждом участке пути перемещаться в любом направлении, то в таком случае мы имеем бы дело с неориентированным графом.
Для решения задания на нахождение кратчайшего пути имеется множество всевозможных алгоритмов. Вышеприведённое решение основывается на алгоритме Дейкстры (англ Dijkstra’s algorithm), но существуют также алгоритм Беллмана-Форда (англ Bellman-Ford algorithm), алгоритм A* (англ A-star) и другие.

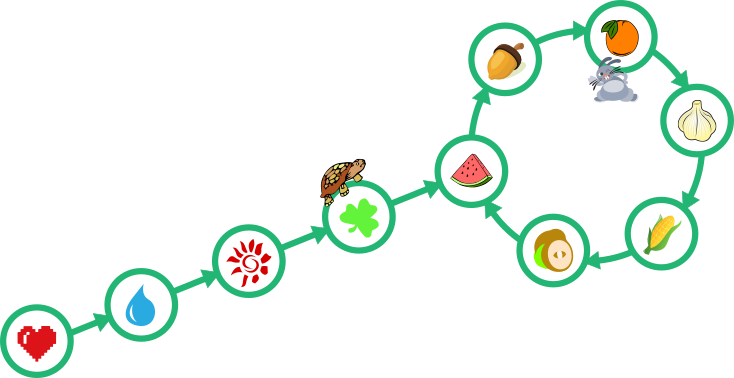
Черепаха и заяц бегут по пути, показанному на рисунке:
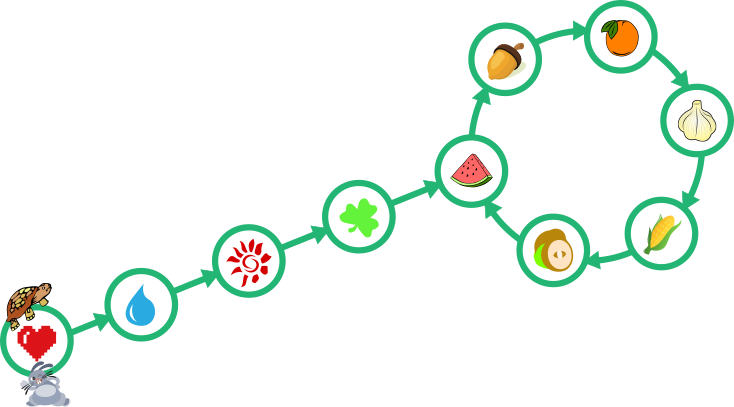
Они стартуют одновременно из обозначенной сердцем точки и следуют указателям. Черепаха за одну минуту проходит одну точку, а заяц — две.
В какой точке они встретятся в следующий раз?
[Raadionupud]
A. 
B. 
C. 
D. 
E. 
F. 
G. Черепаха и заяц никогда не встретятся
Правильный ответ: C.
На нижеприведённых рисунках показано, где будут черепаха и заяц после каждой минуты.
После 1ой минуты
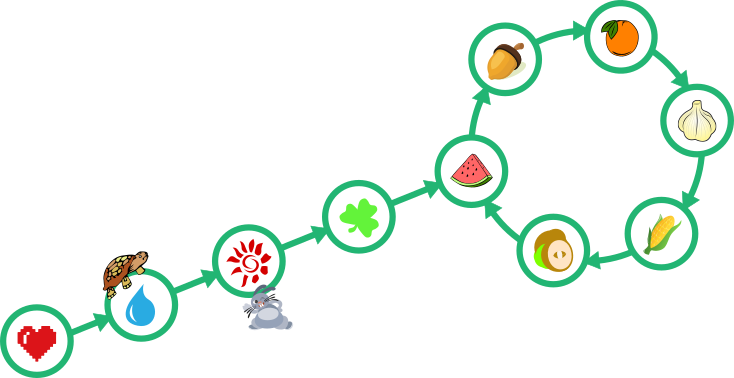
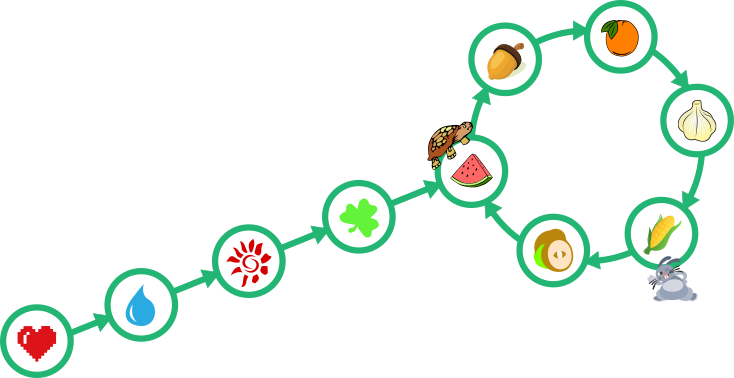
После 2ой минуты
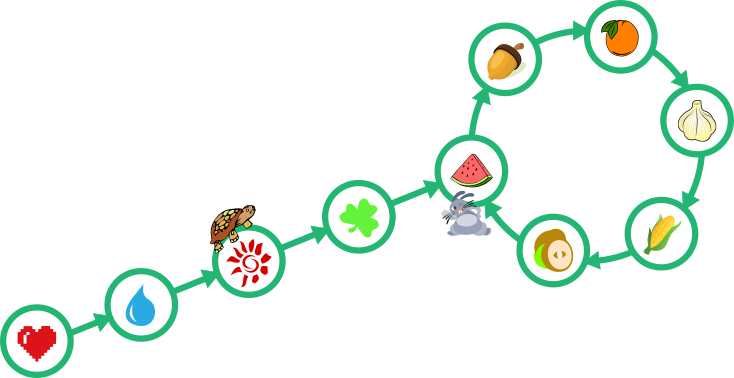
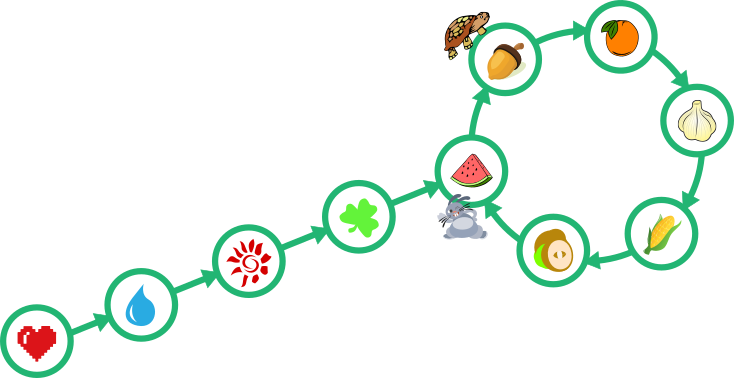
После 3ей минуты
После 4ой минуты
После 5ой минуты
После 6ой минуты
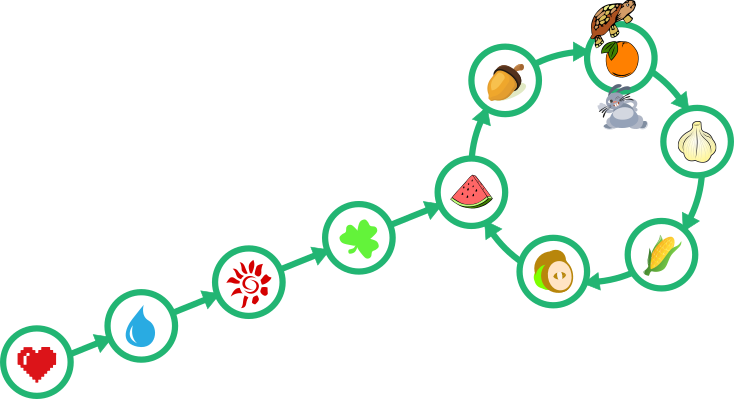
В задании рассматривается одна довольно известная структура данных — граф с направленными циклами — и метод прохода такой структуры.
Связный список (англ linked list) используется для хранения таких данных, которые должны быть соединены между собой последовательно. Элементы такой цепи называются узлами. Примерами таких узлов могут служить шаги по приготовлению какого-то рецепта, ориентиры для прохождения какого-то пути и даже шаги алгоритма для решения какой-то задачи. В случае сохранённых таким образом данных все узлы знают адрес следующего узла, то есть, официально выражаясь, у каждого узла есть ссылка на следующий узел. Обычно связный список линеарен. Это значит, что, если мы начинаем от первого узла и следуем ссылкам, то в итоге мы дойдём до конца и при этом ни разу не окажемся в одном и том же узле дважды.
Если вдруг получится, что какой-то узел мы посетим дважды, то на самом деле мы попадём в цикл. Как же компьютеры распознают наличие цикла? Одна возможность — это использование алгоритма, который так и называется алгоритм "черепахи и зайца" (название является отсылкой на басню древне-греческого философа Эзопа). Этот алгоритм был предложен американским информатиком Робертом В Флойдом. Как и показано в этом задании, две точки перемещаются по списку с разной скоростью — одна из них движется в два раза быстрее, чем вторая. Если они встретятся, то это будет означать наличие цикла в списке, в противном же случае — список линеарен.
Обнаружение циклов является важной задачей в информатике. Так можно проверить, будет ли повторяться работа в написанном нами программном коде, что, в свою очередь, приведёт к тому, что программа не сможет закончить свою работу правильно. Более сложным примером может служить анализ качества работы генератора случайных чисел для обеспечения безопасного шифрования конфиденциальных данных. Обычно такие алгоритмы состоят их предварительной линеарной части цикла и самого цикла. Чем длиннее цикл, тем сильнее алгоритм шифрования и тем сложнее его взломать.

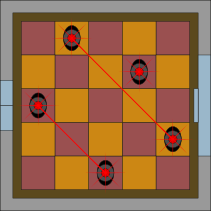
Центральный банк Бобруйска (ЦББ) нуждается в новой охранной системе для защиты от грабителей пространства перед сейфом. Они купили пять датчиков. Каждый датчик излучает восемь лазерных лучей:

Если луч датчика попадает на стену, то ничего не происходит. Если же перед лучом оказывается грабитель, то включается сирена. Сирена также включается и тогда, когда перед лучом какого-нибудь датчика оказывается какой-нибудь другой датчик.
ЦББ хочет расположить пять датчиков на квадратных плитках пола так, чтобы они покрывали все оставшиеся плитки, но при этом не включали бы друг друга. Охранная фирма предложила четыре различных схемы.
Какая из предложенных схем не отвечает заданным требованиям?
[Raadionupud]
A. 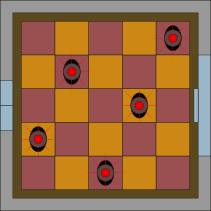
B. 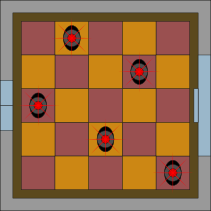
C. 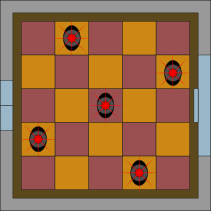
D. 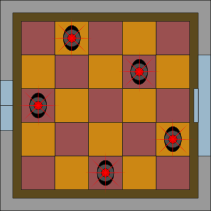
Правильный ответ: D.
В случае отвечающего всем требованиям решения можно заметить, что в каждом ряду и в каждом столбце устанавливается по одному датчику. Это связано с тем, что хотя датчики и излучают лучи по горизонтали и вертикали, они не мешают друг другу. Этого достаточно, чтобы обнаружить грабителя. Однако в действительности датчики излучают ещё лучи и по диагонали. Поэтому необходимо следить, чтобы два датчика не оказались бы на одной и той же диагонали.
Все эти требования соблюдены в случае ответов A, B и C. В случае ответа D две пары датчиков включают сирену, потому что они располагаются на одних и тех же диагоналях:
Данное задание является вариацией известной шахматной задачи о восьми ферзях. С точки зрения информатики, это пример проблемы об удовлетворение ограничений (англ Constraint Satisfaction Problem, CSP). У нас имеются объекты (в нашем случае датчики), у которых могут быть различные значения (в нашем случае местоположения), и для каждого объекта необходимо выбрать такое значение из всех возможных, чтобы оно не противоречило заданным требованиям. Проблемы такого плана обычно возникают при планировании работы роботов, в компьютерной лингвистке при распознавании языка или распределении ресурсов. Такие задачи довольно быстро могут стать сложными и для их решения понадобится компьютер. Компьютеры подходят к решению проблемы аналогично тому, как поступаем мы сами: они пытаются найти решение шаг за шагом. Как только какое-то требование нарушается, они делают один или несколько шагов назад и затем пробуют следующую возможность. Так повторяется до тех пор, пока не будет найдено решение, которое подходило бы под все требование (ограничения).
Как же компьютер решает, мешают ли друг другу два датчика или нет? Это уже задача из области вычислительной геометрии. Пронумеруем плитки пола: ряды сверху вниз, столбцы слева направо. Допустим, что номер ряда и столбца одного датчика будет a и b, а второго — c и d, соответственно. Тогда

Бамбу — ресторан экзотических национальных блюд, где работает два повара. Каждый из них может одновременно заниматься только одним блюдом. Повара всегда готовят блюда в порядке поступления заказов на них. Однако у каждого блюда есть своё время приготовления. Поэтому первым заказанное блюдо может и не быть доставлено к столу клиента первым.
Время приготовления блюд (вместе с подачей) указано ниже:
| Блюдо | Название | Время приготовления |
|---|---|---|
 |
Жареный рис | 5 минут |
 |
Курица сатэ | 14 минут |
 |
Суп из бычьих хвостов | 7 минут |
Однажды в ресторан зашли 5 человек. Официант записал их заказы в следующем порядке:
1ый заказ: суп из бычьих хвостов. 2ой заказ: курица сатэ. 3ий заказ: жареный рис. 4ый заказ: жареный рис. 5ый заказ: суп из бычьих хвостов.
В каком порядке подавались блюда?
[Raadionupud]
A. 1-2-3-4-5
B. 1-3-2-5-4
C. 3-4-1-5-2
D. 1-3-2-4-5
E. 1-4-3-2-5
Правильный ответ: D.
Если мы смоделируем порядок заказов и расположим их все (учитывая и подачу) на временной шкале, то получим следующую таблицу:
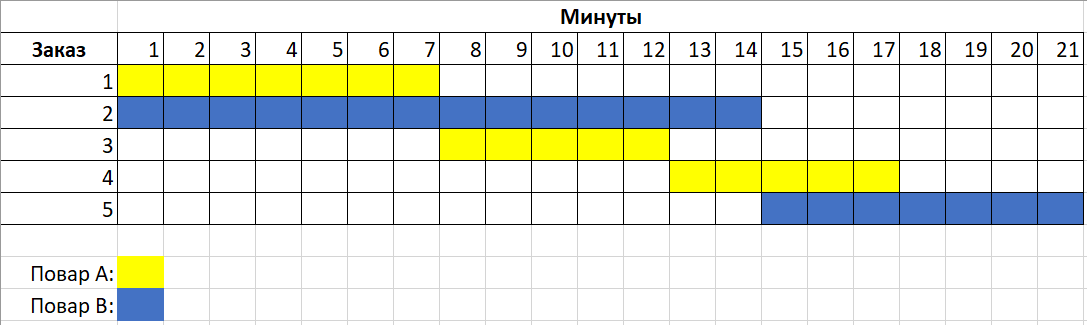
Если мы упорядочим список по времени подачи, то получим ответ 1-3-2-4-5.
Организация работы в ресторане напоминает архитектуру клиент-сервер. Клиент отправляет запрос на сервер, далее сервер отвечает и возвращает запрошенные данные. Время реагирования сервера зависит от многих факторов, например, от типа или размера файла, скорости соединения, коллапсов, и т.д. Поэтому не всегда ответ на первый запрос возвращается к клиенту первым. Также у каждого сервера есть управляемые операционной системой рабочие процессы, которые ограничивают количество одновременно обрабатываемых запросов.

Яна высадила на клумбу слева направо семь цветков. При выборе цветков она опиралась на следующие правила:
В лунку, которая находится с самого левого края, она может высадить любой цветок.
В каждую следующую лунку можно высадить только тот цветок, у которого, в соответствии с приведённой ниже схемой, стрелка из предыдущего высаженного цветка направлена к следующему высаживаемому цветку.

Например, Яна может высадить тюльпан, а рядом с ним нарцисс, потому что на схеме стрелка от тюльпана направлена к нарциссу. Обратный вариант невозможен, потому что нет стрелки от нарцисса к тюльпану.
Какая из следующих клумб создана не по правилам Яны?
[Raadionupud]
A. 
B. 
C. 
D. 
Правильный ответ: D.
Пронумеруем стрелки на схеме Яны следующим образом:

Клумбу A можно высадить, если начать с тюльпана и далее следовать по стрелкам 1, 3, 4, 2, 7 и 7.
Клумбу B можно высадить, если начать с нарцисса и далее следовать по стрелкам 3, 4, 3, 5, 1 и 3.
Клумбу C можно высадить, если начать с тюльпана и далее следовать по стрелкам 1, 3, 5, 1, 2 и 7.
В случае клумбы D мы можем начать с подснежника и далее следовать по стрелкам 4 и 2. Однако у нас нет стрелки от фиалки к тюльпану, и именно поэтому мы не можем закончить эту клумбу по правилам.

Более того, если Яна высадит хотя бы одну фиалку, то во все оставшиеся лунки она должна высадить фиалки, потому что на схеме нет стрелки от фиалки к какому-то другому цветку.
План Яны напоминает автомат (англ state machine), который часто применяется в информатике. Автомат всегда находится в каком-то состоянии, и описание автомата определяет, в какие другие состояния можно переместиться из каждого состояния. По правилам Яны цветок, который был только что высажен, является состоянием клумбы. Так как её схема описывает, какие цветы можно высаживать после каждого цветка, то это и определяет разрешённые переходы между состояниями.
Такие автоматы (некоторые основываются на простых правилах, некоторые на более сложных) часто используются в информатике. Одно из наиболее частых применений — это проверка корректности введённых данных. Например, программа электронных таблиц может использовать автомат, чтобы проверить, является ли введённый пользователем текст числом или корректно записанной формулой. Другой пример — это форма, в которой проверяется поле электронного адреса: присутствует ли там @-знак, нет ли в имени пользователя или домена запрещённых символов, и так далее. Хотя стоит обратить внимание на тот факт, что с помощью автомата можно проверить только формальную корректность адреса. То, существует ли он на самом деле, можно проверить только с помощью отправки запроса на почтовый сервер домена.

Маша нашла ларец с сокровищами, но он закрыт. Чтобы его открыть, надо подобрать правильную комбинацию из трёх фигур. Помоги Маше открыть ларец, если известны следующие комбинации и комментарии к ним.


 Одна фигура правильная и находится на правильном месте.
Одна фигура правильная и находится на правильном месте.

 Ни одна из фигур не является правильной.
Ни одна из фигур не является правильной.

 Две фигуры правильные, но они находятся на неправильных местах.
Две фигуры правильные, но они находятся на неправильных местах.

 Одна фигура правильная, но она находится на неправильном месте.
Одна фигура правильная, но она находится на неправильном месте.

 Одна фигура правильная, но она находится на неправильном месте.
Одна фигура правильная, но она находится на неправильном месте.Какая из следующих комбинаций откроет ларец с сокровищами?
[Raadionupud]
A. 


B. 


C. 


D. 


Правильный ответ: B.
Один из способов решить это задание — это проверить каждую комбинацию на её пригодность.
Комбинации A, C и D не могут быть правильными: третья подсказка указывает, что здесь имеются две правильные фигуры, но ни одна из них не находится на правильном месте. Во всех трёх рассматриваемых комбинациях звезда находится на том же месте, что и в подсказке.
Только комбинация B соответствует всем подсказкам:
Другой способ (более интересный, но немного сложный) не предусматривает изучения предложенных комбинаций, а подразумевает составление решения на основании подсказок.
Начнём с исключения фигур, которые однозначно не подходят для комбинации. Вторая подсказка указывает, что ни одна из фигур не входит в правильную комбинацию. Значит, в нашем ответе не может быть ни одной ёлки, ромба или стрелки.
Последняя подсказка указывает, что одна фигура правильная, но она находится на неправильном месте. Однако нам уже известно, что ёлки или стрелки не может быть в ответе. Значит, правильной фигурой должна быть звезда, но она находится на неправильном месте. Таким образом, для звезды есть два возможных местоположения:


 или
или 


Третья подсказка указывает, что две фигуры подходят, но они находятся на неправильных местах. Одной из них обязательно будет звезда, и теперь становится ясно, что она не может находиться в середине. Значит, мы можем точно сказать, где находится звезда:



Рассуждая таким образом, мы нашли одну фигуру и её правильное местоположение в комбинации.
Далее попробуем найти оставшиеся две фигуры. Первая подсказка указывает, что одна из имеющихся фигур является правильной, и она находится на правильном месте. Ею не может быть стрелка, потому что стрелки среди возможных фигур нет. Значит, правильным может быть один из следующих вариантов:


 или
или 


Мы уже знаем, что в первой клетке должна быть звезда, а значит треугольника там не может быть. Следовательно, именно луна находится на правильной месте:



Четвёртая подсказка указывает, что одна фигура правильная, но находится на неправильном месте. Треугольник бы противоречил первой подсказке. Сердце тоже не подходит — единственно свободное место имеется в середине, а учитывая подсказку, где сердце также находится в середине, мы можем сделать вывод, что это неправильное место. Значит, расположенной в середине фигурой должен быть круг:



Ход рассуждения при решении задания может быть и другим, но все они приведут к тому, что правильным ответом будет B.
В информатике целью распознавания паттернов является проверка соответствия какой-то последовательности элементов определённому паттерну. В данном задании мы следовали подсказкам и составили паттерн, который бы открыл ларец с сокровищами. В обычной жизни с помощью распознавания паттернов проверяют, например, правописание слов.

Турок Махмет плетёт ковры. Он изготавливает ковры с клетчатым узором и размером 6 на 6 клеток.
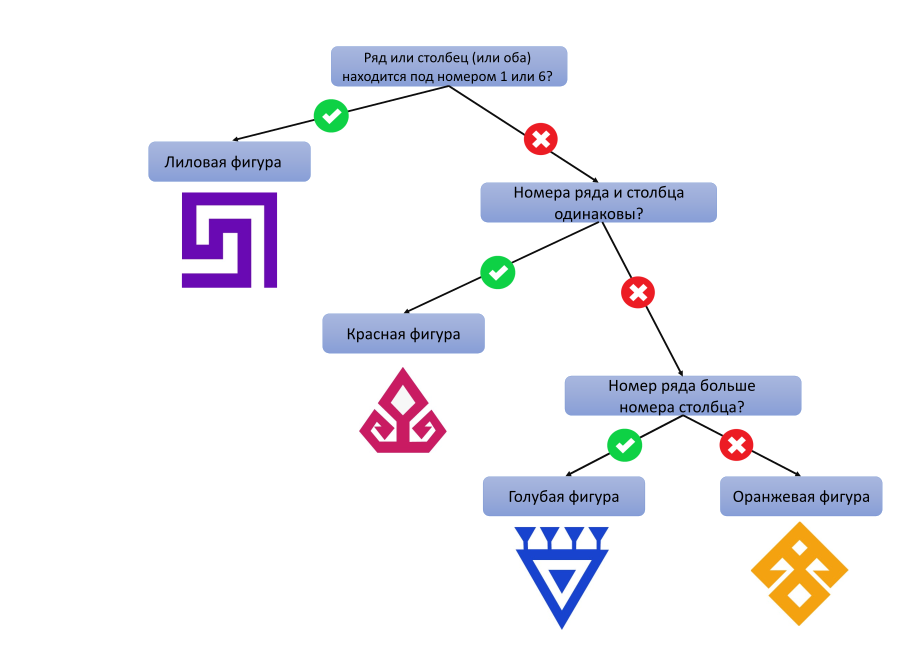
При выборе клетки для фигуры Махмет руководствуется нижеприведённым планом:
Как будет выглядеть сплетённый по этому плану ковёр?
[Raadionupud]
A. 
B. 
C. 
D. 
Правильный ответ: B.
Первый уровень плана указывает на то, что на первой и шестой строчках, а также в первом и шестом столбце должны быть лиловые фигуры:
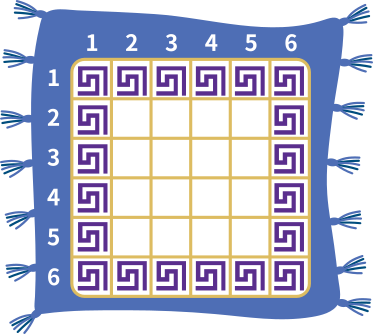
Второй уровень плана указывает на то, что все оставшиеся пустые клетки по диагонали, которая начинается с левого верхнего угла, должны быть заполнены красными фигурами (так как у этих клеток номера рядов и столбцов одинаковы):
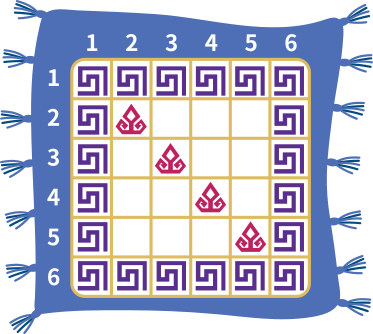
Третий уровень плана указывает на то, что в случае клеток, расположенных от диагонали слева, номера рядов больше номеров столбцов. Значит, там должны располагаться синие фигуры:
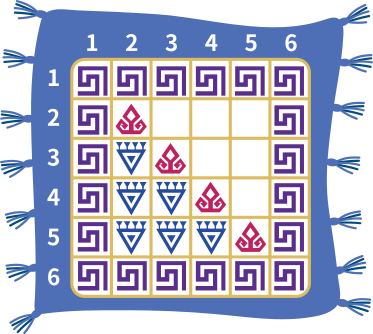
В случае последних оставшихся пустых клеток номер ряда не будет больше номера столбца. Значит, там должны быть оранжевые фигуры. Теперь мы получили ковёр, который и изображён под вариантом B.
В математике и информатике алгоритм означает конечную последовательность дефинированных (определённых) шагов. Обычно его используют при решении каких-то схожих проблем.
Дерево решений (англ decision tree) — это одна из возможностей просто визуализировать структуру алгоритма, который состоит из условных предложений. Это значит, что каждый уровень в таком дереве состоит из вопроса или утверждения: если ответ на этот вопрос будет "да" (или утверждение верно), то выполняется одна ветвь, в противном случае — другая ветвь. Так перемещаются между разными ветвями до тех пор, пока не доберутся до выхода.
Стоит обратить внимание, что часто порядок проверки условий имеет значение. Например, если бы при решении этого задания мы в дереве решений поменяли местами первые два условия, то правильным ответом был бы ковёр под вариантом C.

Бобры решили смастерить себе обычный футбольный мяч.

Они нашли четыре разных кусочка кожи, которые можно было бы для этого использовать.
Из какого кусочка можно смастерить вышеизображённый мяч?
[Raadionupud]
A. 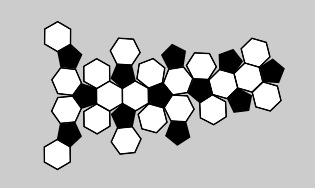
B. 
C. 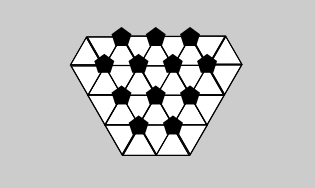
D. 
Правильный ответ: A.
Если мы посмотрим на мяч, то заметим, что все белые части являются шестиугольниками, а все чёрные — пятиугольниками. Значит, мы можем исключить варианты B (здесь все имеющиеся чёрные фигуры являются шестиугольниками) и C (здесь используются треугольные белые части вместо шестиугольных).
Также можно заметить, что между двумя чёрными пятиугольниками имеется только одно ребро шестиугольника. Значит, вариант D не подходит, потому что два чёрных пятиугольника отделены друг от друга по меньшей мере двумя шестиугольниками.
Следовательно, остаётся только вариант A.
Обратите внимание, что на рисунке кусочки паттернов A и D не полностью соединены между собой. Это всё потому, что мы имеем дело с изображением трёхмерной поверхности в двухмерном пространстве. Всё соединиться идеально, как только мы вырежем кусочки и сложим их вместе.
Распознавание паттерна — это один из краеугольных столпов информатики. Нахождение в задании повторяющихся паттернов намного облегчает решение таких заданий. С помощью распознавания паттерна находятся сходства и различия объектов — это похоже на человеческое восприятие. Например, человек различает кошку по свойствам, характерным именно для кошки. Так же и компьютер на основании признаков, характерных для кошки, определяет, что перед нами картинка с кошкой.
Распознавание паттерна помогает людям разных профессий. Например, в медицине этот подход используется для диагностирования болезней, для предсказания рисков заболеваний и т.д.; в сельском хозяйстве определяются болезни растений по сделанным фотографиям листочков.

В приведённом тексте пробелы отмечены символом '·', а переходы на новые абзацы символом '¶'. Неотмеченные переходы на новую строку автоматически добавляются текстовым процессором.
Статья·1.·Эстония·—·самостоятельная·и·независимая·демократическая·республика·,где·
носителем·верховной·власти·является·народ.·Самостоятельность·и·независимость·Эстонии·
непреходящи·и·неотъемлемы.¶
Статья·2.·Территория,территориальные·воды·и·воздушное·пространство·Эстонского·
государства·—·единое·и·неделимое·целое·.·По·своему·государственному·устройству·
Эстония·единое·государство,·административно-территориальное·деление·которого·
устанавливается·законом.¶Сколько существует пар слов, между которыми при оформлении текста пробелы были использованы неправильно?
(Если в одной паре допущено несколько ошибок, то считай это за одну ошибку.)
[Täisarv]
Правильный ответ: 3.
Первая ошибка — это 'республика·,где', где пробел должен быть после запятой, а не перед.
Вторая ошибка — это 'Территория,территориальные', где пробел должен быть после запятой.
Третья ошибка — это 'целое·.·По', где пробела не должно быть перед точкой.
Помимо того, что неправильное использование знаков препинания является ошибкой правила правописания, оно также может привести к неудобствам, связанным с автоматическим переносом строки во время обработки текстов на компьютере. Если не поставить пробел после запятой или точки, то при необходимости текстовой редактор не сделает в этом месте разрыва строки; это может повлиять на выравнивание текста. Если поставить пробел перед запятой или точкой, то при автоматическом переходе на новую строку текстовой редактор может перенести знак препинания в начало следующей строки, а это выглядит некрасиво.
С точки зрения правописания мы можем обсудить, имеется ли в случае 'республика·,где' одна ошибка (пробел и запятая в неправильном порядке) или две ошибки (лишний пробел перед запятой, отсутствие необходимого пробела после запятой). Чтобы было ясно и понятно, то вместо количества ошибок в задании спрашивается количество пар слов, где что-то не так. Такая же точность требуется во многих ситуациях, когда разные стороны (будь то люди или компьютеры) должны понимать правило одинаково — например, когда оценивание за диктант на экзамене по эстонскому языку основывается на количестве ошибок.

Рассмотрим следующий лист электронной таблицы, где в некоторых ячейках содержатся числа, а в некоторых — формулы:
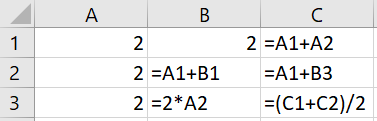
Какое значение появится в табличной ячейке C3?
[Täisarv]
Правильный ответ: 5.
Для вычисления значения ячейки C3 нам понадобятся значения ячеек C1 и C2. У нас уже есть все необходимые данные для вычисления значения ячейки C1: 2+2=4. Для вычисления значения ячейки C2 нам понадобится значение ячейки B3. На основании имеющихся данных мы получим 2*2=4 для B3, затем 2+4=6 для C2 и, наконец, (4+6)/2=5 для C3.
Нам не понадобилось значение ячейки B2, поэтому мы оставили его невычисленным.
Формулы, используемые в рабочих листах электронных таблиц, позволяют автоматизировать повторяющиеся вычисления, экономя время пользователей и уменьшая количество ошибок, вызванных вычислениями вручную.

Бобрята Катя и Миша изучают текстовый пользовательский интерфейс, то есть использование командной строки в компьютере.
Миша в своём компьютере просматривает файлы как с помощью командной строки, так и графического интерфейса:
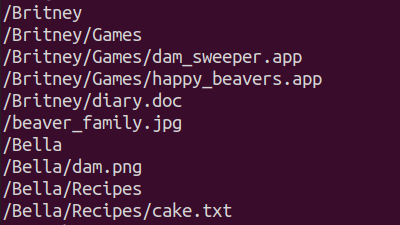
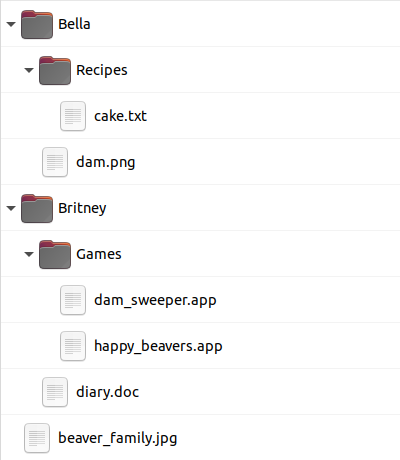
Катя в своём компьютере просматривает файлы только с помощью командной строки:
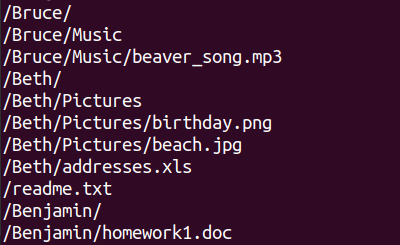
Что из нижеприведённого соответствовало бы отображению файлов Кати с помощью графического интерфейса?
[Raadionupud]
A. 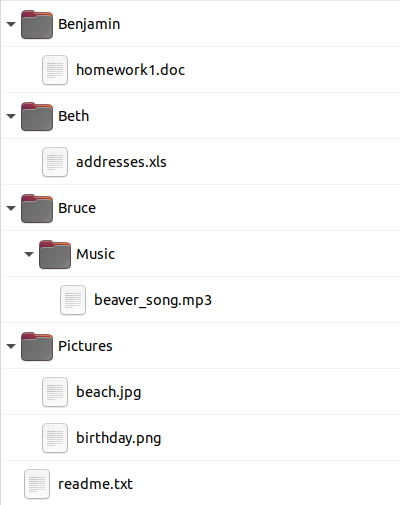 B.
B. 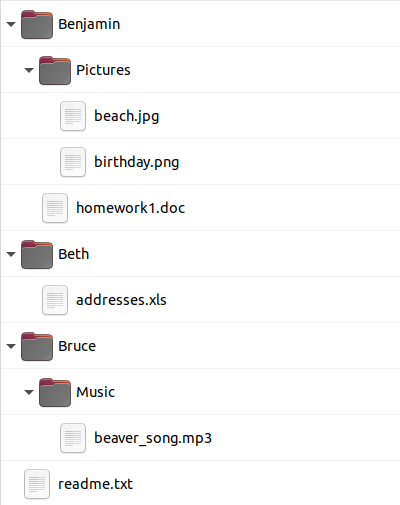 C.
C. 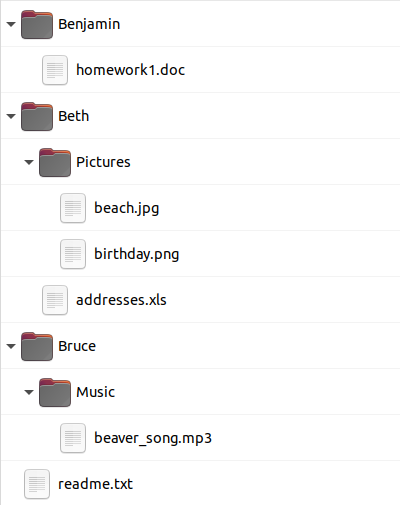 D.
D. 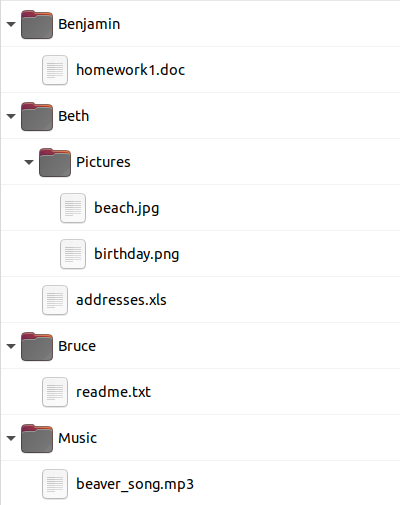
Правильный ответ: C.
Варианты A и B показывают расположение папки "Pictures" в неправильном месте. В случае варианта D в неправильном месте располагаются папка "Music" и файл "readme.txt".
В компьютере файлы хранятся в иерархической структуре. В ней имеются файлы и папки; каждый файл находится в одной папке и (если не брать в расчёт самую верхнюю — корневую — папку) каждая папка тоже находится в одной папке. Конечно, в каждой папке может быть несколько файлов и папок. Идея такой системы очень стара — такой подход использовался ещё до изобретения компьютеров для хранения бумажных документов. Такая структура позволяет лучше организовать управление правами доступа — доступ можно дать к одной папке с имеющимися в ней папками.
Сегодня используются и другие системы. Например, электронные сообщения можно "пометить" (англ tagged) и у одного сообщения может быть несколько различных пометок.
Файловая структура — это один из примеров древовидной структуры. Деревья — это очень распространённый во многих программах способ для организации и хранения иерархической информации.

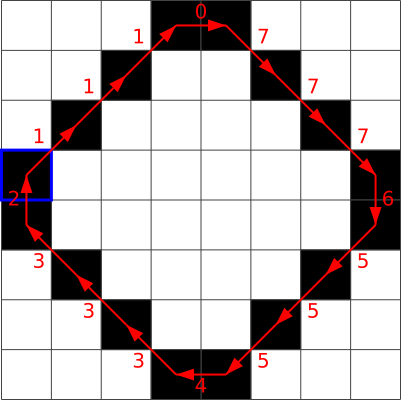
Цепной код — это экономный способ представления контуров (границ) на чёрно-белых изображениях. Суть заключается в выборе одного чёрного пикселя и сохранении на каждом этапе прохождения контура по движению часовой стрелки направления, которое позволит добраться до следующего чёрного пикселя.
Направления отмечены цифрами следующим образом:
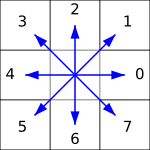
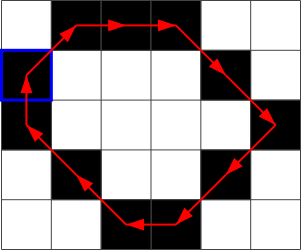
Например, если на нижеприведённом изображении стартовый пиксель отмечен синей рамкой, то дальше можно двигаться в отмеченных красными стрелками направлениях. Как результат, цепной код будет 1, 0, 0, 7, 7, 5, 5, 4, 3, 3, 2.
Рассмотрим теперь такое изображение:

Что из приведённого будет цепным кодом этого изображения?
[Raadionupud]
A. 1, 1, 1, 0, 7, 7, 7, 6, 5, 5, 5, 4, 3, 3, 3, 2
B. 1, 1, 0, 0, 7, 7, 6, 6, 5, 5, 4, 4, 3, 3, 2, 2
C. 6, 7, 7, 7, 0, 1, 1, 1, 2, 3, 3, 3, 4, 5, 5, 5
D. 0, 1, 1, 0, 7, 7, 7, 6, 5, 5, 5, 4, 3, 3, 3, 0
Правильный ответ: A.
Цепной код — один из методов для представления объектов на основании их контуров. Этот код задаётся с помощью стартового пикселя и последовательности векторов-направлений. Эти направления в сторону следующего чёрного пикселя определяются при каждом шаге по мере прохождения контура и могут быть направлены влево, вправо, вверх, вниз или по диагонали. Преимуществом цепного кода является сохранение необходимой информации при очень большой экономии объёма данных. Первым идею цепного кода предложил в 1961 году Фримен, и поэтому код больше известен как цепной код Фримена (англ Freeman Chain Code, FCC).
Одной из областей применения цепного кода является распознавание цифр. Во-первых, этот код позволяет представлять объекты более компактно, а во-вторых, проведение сравнения цепных кодов намного легче, чем сравнение изображений. К тому же из цепного кода можно получить единичные свойства изображённого объекта. Цепные коды представляют собой сжатие без потерь и сохраняют всю информацию, необходимую для быстрого и эффективного анализа паттернов.

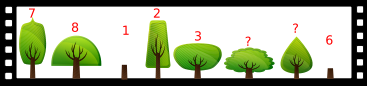
Тиша был на окружённой восемью деревьями поляне и сделал 360-градусный снимок деревьев.

Через несколько дней Тиша вновь пришёл на эту поляну и увидел, что два дерева уже спилили. Он сделал похожий снимок, но начал свой 360-градусный круг с немного другого направления по сравнению с прошлым разом.
Какой их приведённых снимков сделал Тиша во второй раз?
[Raadionupud]
A. 
B. 
C. 
D. 
Правильный ответ: C.
Если мы пронумеруем имеющиеся на оригинальном снимке деревья, то получим следующее:

Если немного изменить точку обзора, то получим снимок, где деревья располагаются всё в том же самом порядке, но немного смещены. Для наглядности вновь пронумеруем имеющиеся на снимке деревья, причём на обоих снимках те же номера будут соответствовать тем же деревьям.

Теперь проверим, все ли деревья на снимках пронумерованы таким же образом и в правильном порядке.
В случае варианта A спилены деревья под номерами 1 и 5, а дерево под номером 4 имеет другую форму по сравнению с оригиналом.

На снимке B спилены деревья под номерами 6 и 3, а дерево под номером 1 имеет другую форму по сравнению с оригиналом.

Если мы сравним оригинал с вариантом C, то заметим, что деревья 4 и 3 спилены, а остальные деревья находятся в правильном порядке.

В случае варианта D спилены деревья под номерами 1 и 6, а деревья под номерами 4 и 5 имеют другую форму по сравнению с оригиналом.
Для решения этого задания требуется найти паттерн, который бы описывал порядок деревьев. Далее этот паттерн необходимо соотнести с предложенными вариантами ответов. Умение распознать паттерн позволяет нам найти ошибки в последовательности. В данном случае важно найти порядок деревьев. Если соотнесём полученный паттерн с различными вариантами и найдём разницу, то это будет называться ошибкой. Такой процесс поиска называется распознаванием ошибок, и он является неотъемлемой частью тестирования программ. Если часть информации отсутствует (как, например, в данном случае, где часть деревьев была спилена), то распознавание ошибки становится более сложной задачей.
Copyright © 2022 Bebras – International Challenge on Informatics and Computational Thinking.
Licensed under Creative Commons Attribution-ShareAlike 4.0 International License.
Flag icons by GoSquared.