

Tiina, kes on pime, jalutab üksi mööda linnatänavaid, kasutades rääkivad prille.
Rääkivatel prillidel on kaamerad ja intelligentne objektide tuvastamise süsteem. Prillid suudavad ära tunda nelja tüüpi objekte: maja, puu, tänav ja muru. Kui Tiina siseneb uude ruutu, teatavad prillid talle (just selles järjekorras), mis on temast vasakul, tema ees ja temast paremal, näiteks "puu tänav maja".
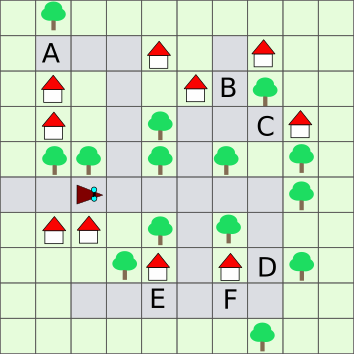
Tiina alustab kolmnurgaga tähistatud ruudust (olles näoga kaardi parema ääre suunas) ja kuulab rääkivate prillide teateid. Ta kuuleb selliseid teateid:
Nii jõuab Tiina ühte kaardil tähega tähistatud ruutudest.
Millisesse ruutu Tiina jõudis?
[Raadionupud]
A. A
B. B
C. C
D. D
E. E
F. F
Õige vastus on: B.
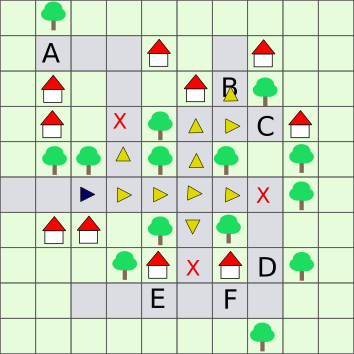
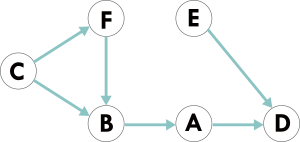
Vastuse leidmiseks on erinevaid lähenemisi. Üks võimalus on alustada stardipunktist ja otsida teed, mis sobib rääkivatelt prillidelt saadud infoga. Kuna prillid ei ütle, kuhupoole Tiina liikus, peab igal sammul vaatama kõiki ümbritsevaid ruute ja kontrollima, kas ümbruse kirjeldus vastab rääkivate prillide omale. Näiteks vaadates teed, mis viib ruuduni A, näeme, et pärast kolmandat teadet ("puu tänav puu") peaks järgmine olema "muru tänav puu", kuid prillid ütlesid hoopis "tänav tänav tänav". Seega Tiina ei läinud punkti A ning peame uurima teisi variante. Teeme nii seni, kuni oleme läbi proovinud kõik teed või kuni jõuame ilma vastuoludeta mõne sihtruudu juurde kohale. Joonisel on näha kõikvõimalikud teed, mida Tiina võis käia, ja punane X tähistab ruutu, kus tekib vastuolu.
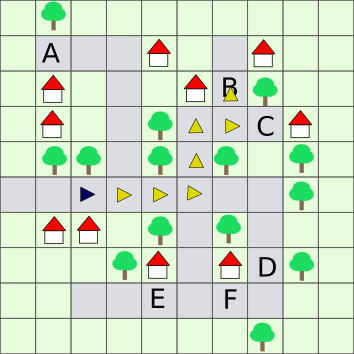
Teine võimalus on kontrollida kõiki kuut sihtruutu: neist ainult B ja D vastavad teatele "maja tänav puu". Samas puuduvad ruudul D naabrid, mis vastaksid nimekirjas eelviimasele teatele "tänav tänav puu". Seega pidi Tiina minema ruutu B.
Ülesanne näitab, kuidas rääkivate prillide teadete nimekiri on piisav allikas sihtruudu määramiseks, kuigi need teated ei ütle otseselt, millises suunas Tiina liikus. Sageli on keeruline hinnata, kui tundlik on inimeste kohta kogutud info, eriti ruumiliste ja geograafiliste andmete puhul.
Objektide tuvastamine on arvutiteaduses oluline teema. Tehisintellektiga varustatud süsteeme võib treenida tuvastama erinevaid objekte nagu majad, puud ja teepind. Arvatavasti oskab ka Sinu nutitelefoni kaamera ära tunda inimeste nägusid ja neid ruudukestega märkida. Iseliikuvad autod peavad enda ümbruses tuvastama inimesi, teisi autosid, liiklusmärke ja muid objekte, et selle põhjal otsustada, millises suunas edasi liikuda. Vaegnägijate ja pimedate abistamiseks suudavad süsteemid lisada automaatselt pildikirjeldusi (ingl Automatic Alt Text, AAT). Kuigi "rääkivad prillid" kuuluvad praegu veel ulme valda, on juba olemas prototüübid, mis püüavad seda ideed realiseerida.

Trips-traps-trull on kahe mängija mäng. Mängijad joonistavad 3 korda 3 ruudustikku vaheldumisi enda sümboli (vastavalt X või O), kusjuures joonistada võib ainult tühjadesse ruutudesse. Võitja on see, kes suudab esimesena moodustada kolmest enda sümbolist rea, veeru või diagonaali. Kui kumbki seda ei suuda ja kõik ruudud saavad täidetud, lõpeb mäng viigiga.
Joonisel on näha näide ühest X võiduga lõppenud mängust, kus igas seisus on viimane käik esile tõstetud.
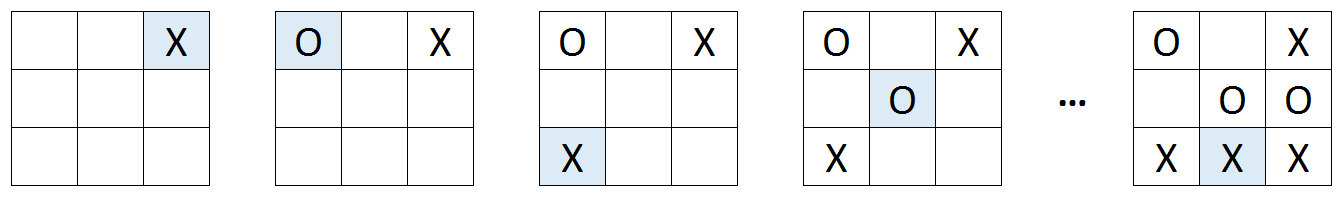
Mängu lõpus ruudustikku jäädud seisu nimetame lõppseisuks. Aga mitte kõik juhuslikult sümbolitega X ja O täidetud mängulauad pole reeglitele vastavad lõppseisud.
Milline järgnevatest on trips-traps-trulli reeglitega kooskõlas olev lõppseis?
[Raadionupud]
A. 
B. 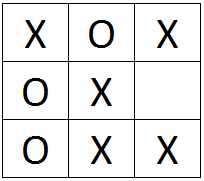
C. 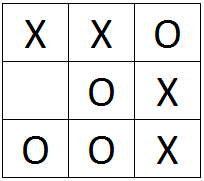
D. 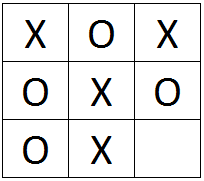
Õige vastus on: C.
Vastus C on õige: mängija O on võitnud ja seejärel mäng lõppes.
A pole korrektne seis: mängija X on võitja, kuid mängija O on lisanud rohkem sümboleid kui X. Kuna võitja käib alati viimasena, teeb ta kas rohkem või sama palju käike kui vastane, aga mitte kunagi vähem.
B pole korrektne seis: laual on 5 X-i, kuid ainult 3 O-d. Kuna käiakse kordamööda, saab erinevus sümbolite arvus olla ainult kas 0 või 1.
D pole lõppseis: võitja pole veel selgunud, kuid kõik väljad pole ka täidetud.
Me lahendasime ülesannet, kontrollides nelja pildi vastavust mängureeglitele. Reeglitest saame me tuletada omakorda nõuded lõppseisule, näiteks:
Kui mõni pilt satub mõne toodud nõudega vastuollu, ei saa see olla korrektne lõppseis.
Reeglid on informaatikas andmetöötluse puhul väga olulised. Olemas on näiteks kindlad reeglid, millise vormiga peavad olema telefoninumbrid, isikukoodid, pildifailid. Kui püüame avada mõnda faili pildiredaktoris, kontrollib programm esmalt, kas faili sisu vastab pildifailivormingu reeglitele.
Teiselt poolt on ka oluline, et programmi seatud reeglid poleks liiga ranged. Näiteks USA programmeerijate loodud veebipoe kontaktandmete vorm võib nõuda, et telefoninumber peaks koosnema 3-kohalisest piirkonnakoodist ja 7-kohalisest abonendi numbrist, aga Eesti telefoninumbrid on teise struktuuriga ja neid ei saaks sinna sisestada.

Ühe klassi õpilased suhtlevad oma klassikaaslastega vastavalt joonisele. Näiteks õpilane H suhtleb päeva jooksul ainult D, E ja F-ga.
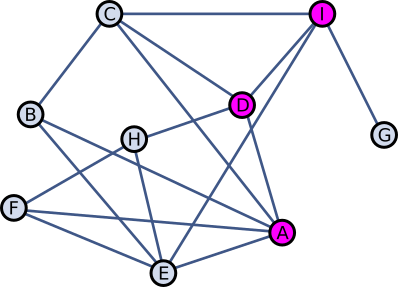
Esmaspäeval tuli tööle uus matemaatikaõpetaja, keda kolm õpilast A, D ja I hakkasid tema soengu tõttu kohe kutsuma Miss Infinityks. Hüüdnimi levis õpilaste hulgas nii, et iga õpilane, kelle vestluskaaslastest rohkem kui pooled seda kasutasid, hakkas ka ise järgmisel koolipäeval uut õpetajat sel viisil hüüdma.
Milline oli esimene päev, kui kõik selle klassi õpilased kasutasid hüüdnime Miss Infinity?
[Raadionupud]
A. Teisipäev
B. Kolmapäev
C. Neljapäev
D. Reede
E. Järgmine esmaspäev
Õige vastus on: D.
Jälgime hüüdnime levikut.
Teisipäeval hakkasid seda hüüdnime kasutama õpilased G ja C. G suhtleb ainult ühe kaasõpilasega, nimelt I-ga, kes kasutas uut hüüdnime juba esmaspäeval. C vestles nelja kaasõpilasega ja neist kolm kasutasid esmaspäeval uut hüüdnime. Kolm neljast on rohkem kui pool, seega hakkas ka C teisipäeval uut hüüdnime kasutama.
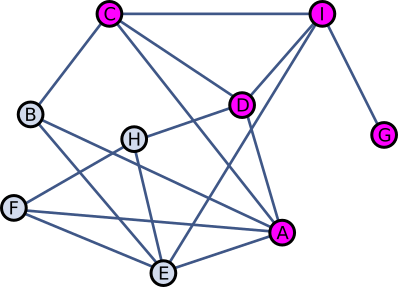
Kolmapäeval hakkas uut hüüdnime kasutama B.
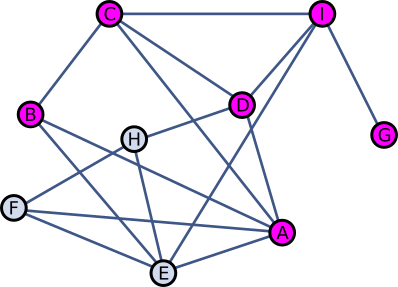
Neljapäeval tegi sellega algust E.
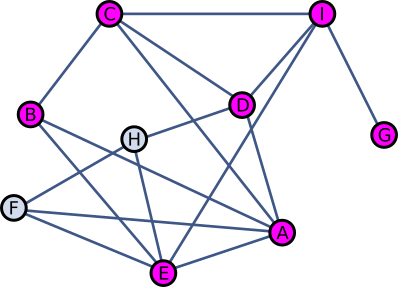
Reedel nimetasid uut matemaatikaõpetajat Miss Infinityks ka F ja H.
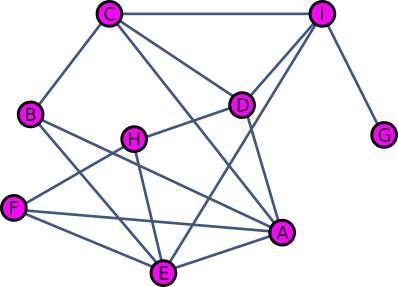
Sotsiaalvõrgustikud mängivad info, ideede ja seisukohtade levitamisel suurt rolli. Mõte, mis ilmub sotsiaalvõrgustikku, kas levib kiiresti või kaob. Info sotsiaalvõrgustikes levimise kiiruse uurimine on väga populaarne suund informaatikas ja selle kiiruse suurendamine on kujunemas omaette oluliseks haruks reklaamimaailmas.
See ülesanne keskendub nn. lävendimudelile (ingl threshold model), milles igal isikul on lävend ehk kontaktide hulk, mis peab olema aktiivne (praegusel juhul tähendab see uue hüüdnime kasutamist), et ka isik ise muutuks aktiivseks (ehk hakkaks seda hüüdnime kasutama).

Kuus kobrast A, B, C, D, E ja F ehitasid igaüks jõele oma tammi. Ühel päeval tuli torm ning osa palkidest, millest tammid olid ehitatud, uhuti allavoolu. Õnneks oli iga palk märgistatud ehitaja nimega, näiteks kopra A ehitatud tammi ehitusmaterjalil oli täht "A".

Pärast tormi kogus iga kobras oma tammi juurest võõrad palgid kokku, et need omanikele tagasi anda. Tulemus oli selline:

Kui otsustada kobraste kogutud palkide järgi, siis millises järjekorras on tammid, kui alustada kõige kõrgemal olevast tammist ja liikuda allavoolu?
[Raadionupud]
A. A→B→C→D→E→F
B. C→B→F→A→D→E
C. C→F→B→D→A→E
D. E→C→F→B→A→D
Õige vastus on: D.
Palgid liiguvad jões allavoolu. Seega, kui kobras X leidis kopra Y ehitusmaterjali, siis pidi kopra X tamm asuma allpool kui kopra Y oma. Nii võime teise pildi põhjal koostada skeemi (nn. graafi), mis näitab tammide asukohtade omavahelisi suhteid. Skeemil tähistame noolega veevoolu suunda kahe tammi vahel.
Nagu näeme, ei suundu ühtki noolt tammide C ega E suunas, seega ainult need saavad olla esimesed tammid ja variant A ei sobi. Variant B on vale seetõttu, et skeemi järgi peaks F olema kõrgemal kui B. Variant C ei sobi samuti, kuna selle järgi peaks D olema E-st kõrgemal, kuid skeemil on vastupidi. Õige saab olla ainult variant D.
Suunatud graaf (ingl directed graph) koosneb tippudest ja suunatud servadest ehk kaartest. Selles ülesandes vaatleme iga tammi kui tippu, kaared aga iseloomustavad palkide liikumise suunda. Sellist tammide järjestamist vastavalt jõevoolu suunale ehk üldisel juhul tippude järjestamist vastavalt kaarte suunale nimetatakse topoloogiliseks järjestamiseks (ingl topological ordering).
Topoloogilisi järjestusi võib ühel graafil olla mitu. Näiteks selles ülesandes on tammide C, F, B, A ja D omavaheline järjekord kindel, aga tamm E võib ülesande andmete põhjal olla teiste vahel viies erinevas kohas.
Teiselt poolt mõnes suunatud graafis topoloogilist järjestust ei olegi. See juhtub siis, kui graafis on nn. tsükkel: selline kaarte jada, millega jõuame mingist tipust alustades samasse tippu tagasi.
Üks topoloogilise järjestuse leidmise viis on Kahni algoritm: kõigepealt valime mingi tipu S, mis pole ühegi kaare lõpptipp, seejärel kustutame selle koos temast väljuvate kaartega ja kordame neid samme, kuni graaf on tühi. Kahni algoritm võimaldab ka kontrollida, kas graafis on tsükleid: kui jõuame algoritmi täitmise käigus seisu, kus graaf ei ole veel tühi ja iga allesjäänud tipp on mõne kaare lõpptipp, siis selles graafis tippude topoloogilist järjestust ei ole.
Informaatikas kasutatakse topoloogilist järjestamist näiteks protsesside tööde järjekorra koostamisel.

Koprapere valdused koosnevad 21-st kanalist. Kanalitest on vaja välja korjata kokku 31 kivi. Kõik koprad alustavad tiigist, ujuvad kanaleid mööda kivideni ja viivad need koju.

Kivid on rasked, üks kobras suudab neist korraga kaasas kanda vaid ühte või kahte. Ühest kanalite lõikumiskohast teiseni ujumiseks kulub kobrastel alati täpselt üks tund. Peale ühist starti peavad koprad kõik kivid koju viima nelja tunniga.
Kui palju kopraid on selleks minimaalselt vaja?
[Raadionupud]
A. 14 kobrast
B. 18 kobrast
C. 20 kobrast
D. 24 kobrast
Õige vastus on: A.
Kuna kanalite ja kivide täpne kuju pole ülesande lahendamise seisukohalt oluline, võime ülesande tekstis oleva joonise lihtsustada allolevaks skeemiks, kus kanaleid esitavad jooned ja kivihunnikuid arvud.

Lahenduse leidmiseks paneme kõigepealt tähele, et järgneval skeemil punasega näidatud teed ujudes saavad 2 kobrast 4 kivi koju viia vaid kahe tunniga ja siis jääb neil parasjagu aega, et sinist teed mööda edasi-tagasi ujudes veel 4 kivi ära viia.
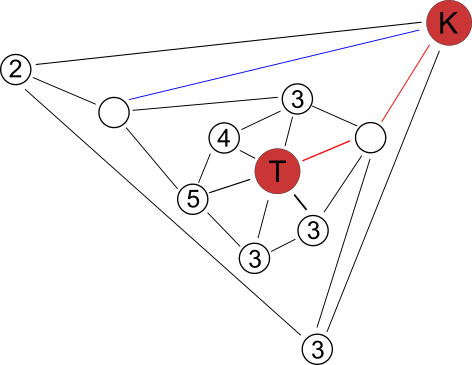
Samal ajal võivad ülejäänud koprad liikuda järgneval skeemil kujutatud viisil: 3 kobrast võivad liikuda mööda punast teed ja viia koju 6 kivi; järgmised 3 kobrast võivad liikuda mööda sinist teed ja viia koju samuti 6 kivi; järgmised 2 kobrast võivad liikuda mööda rohelist teed ja viia koju 4 kivi; viimased 4 kobrast võivad liikuda mööda violetset teed ja viia koju viimased 7 kivi.
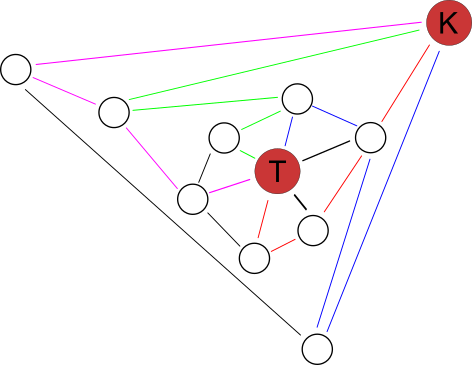
Sellega oleme näidanud, et 14 kobrast saavad tõesti nelja tunniga kõik kivid koju viia. Kuidas me aga teame, et väiksema arvu kobrastega see võimalik ei ole? Selleks on vaja kolme tähelepanekut.
Esiteks, kord juba koju jõudnud kopral kulub sealt uuesti välja tulekuks ja lisakivide koju viimiseks vähemalt kaks tundi (vähemalt üks tund kivideni ja vähemalt üks tund kividega koju tagasi ujumiseks). Kuna kogu kivivedu peab olema lõpetatud nelja tunniga, tähendab see, et stardist koju ujumiseks ei tohi ta ka kulutada rohkem kui kaks tundi.
Teiseks, stardist koju on täpselt üks tee, mille läbimiseks kulub kaks tundi, ja pole ühtki teed, mille läbimiseks kuluks vähem. Kuna ainsal piisavalt lühikesel teel on 4 kivi, tähendab see, et nelja tunni jooksul jõuavad kaks koormat kive koju viia ainult 2 kobrast.
Kolmandaks, kanalites on kokku 31 kivi. Kui iga kobras viiks koju 2 kivi, oleks meil kokku vaja 16 kobrast (31/2=15,5, aga ilmselgelt ei saa viimase kivi koju viimiseks kasutada poolt kobrast!). Kuna kopraid, kes jõuavad kaks koormat kive koju viia, on ainult 2, ongi meil vaja minimaalselt 16–2=14 kobrast.
Ülesande tekst (ja selles olev joonis) kirjeldavad värvikat lugu kobrastest ja kividest. Teadlase esimene samm on eemaldada kõik ebaolulised detailid ja jätta alles ainult lahenduse leidmiseks vajalik info. Nii lihtsustuvad kanalid joonteks ja kivihunnikud nende suurusi näitavateks arvudeks. Sellist andmete esitamise viisi nimetatakse graafiks ja seda kasutatakse arvutiteaduses palju.
Selles ülesandes pidime leidma lahenduse kivide vedamiseks võimalikult vähese arvu kobrastega. Ülesandeid, kus on vaja leida mingi kriteeriumi järgi parim lahendus, nimetatakse üldiselt optimeerimisülesanneteks. Nende lahendamiseks on olemas mõned väga üldised meetodid, aga need põhinevad kõigi võimalike variantide proovimisel ja võtavad väga kaua aega. Sageli on ülesande eripärast lähtuvate tähelepanekutega võimalik optimaalse lahenduseni jõuda palju kiiremini.
Paljude ülesandetüüpide jaoks on välja mõeldud just neile sobivad spetsiaalsed lahendusmeetodid. Mõnd liiki ülesannete jaoks on teada, et olemasolevad meetodid ongi parimad võimalikud, aga paljude ülesandetüüpide korral see nii ei ole ja teadlased otsivad praegugi järjest uusi ja paremaid lahendusviise.

Me võime esitada arvude loendit 3, 5, 2, 4, 1 visuaalselt näiteks sellisel kujul (väikesed punased numbrid ülaservas on elementide indeksid ehk asukohad loendis):

Me võime 2. kohal oleva arvu tähistamiseks kirjutada (X 2). Seega meie näite puhul on (X 2) arv 5 ja (X 5) on 1.
Me võime indeksi anda ka kaudselt, näiteks (X (X 3)) on 5, sest (X 3) on 2 ja seega (X (X 3)) = (X 2) = 5.
Siin on kolm loendit: A, B ja C.

Millist arvu tähistab (A (B (C 3)))?
[Täisarv]
Õige vastus on: 4.
Kuna (C 3) = 4, siis (B (C 3)) = (B 4) = 3 ning (A (B (C 3)) = (A (B 4)) = (A 3) = 4.
Andmestruktuurid on programmeerimises olulised. Eriti kasulikud on sellised struktuurid, mis suudavad säilitada elementide järjendeid. Järjendeid saab ka omavahel siduda nii, et ühe järjendi elemendid sisaldavad teise järjendi elementide indekseid. Tundub segane, kuid sammhaaval arvutades, nagu eelpool näidatud, pole tegelikult kuigi raske. Samas on selline viis elementide poole pöörduda on sageli väga kasulik.

Koodikobraste lahes on tuletornid valgustatud erilisel viisil. Igal majakal on oma unikaalne kood, mille järgi ta vilgub. Nii saavad meremehed lihtsalt tuvastada, millist majakat nad parajasti vaatavad.
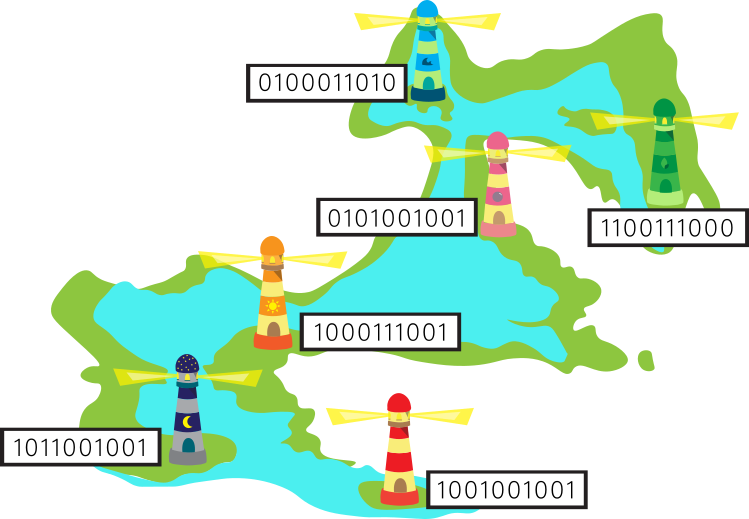
Näiteks kui tuletornil on kood "1011001001", siis esimese kümne sekundi jooksul lülitub ta sisse ja välja nii: 1. sekundil põleb, 2. sekundil ei põle, 3. sekundil põleb, 4. sekundil põleb, 5. sekundil ei põle, 6. sekundil ei põle, 7. sekundil põleb, 8. sekundil ei põle, 9. sekundil ei põle, 10. sekundil põleb.
Iga järgmise 10 sekundi jooksul see muster kordub.
Kui kõik tuletornid hakkavad tööle samal ajal, siis mitmendal sekundil põlevad kõigi majakate tuled korraga?
[Täisarv]
Õige vastus on: 7.
Kui me kirjutame kõigi majakate koodid üksteise alla, on lihtne märgata, et kõigis koodides on seitsmendal kohal number 1 (mis tähistab seda, et tuli majakas põleb).
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 |
Informaatikas tuleb meil sageli kodeerida mingeid sündmusi või olekuid arvude või tähtede abil, sageli kasutame selleks ka erinevaid arvusüsteeme. Kui näiteks leiab aset mingi sündmus, võime me selle tähistamiseks omistada mõnele muutujale sobiva väärtuse, et oleks selge: selline sündmus leidis aset või saavutati mingi olek. Hiljem programmi töö käigus saame sellest väärtusest lähtudes käivitada ühe või teise funktsiooni.

Kobras Siiri ja tema sõbrad otsustavad mängida mängu nimega "Süüta lamp!". Mängul on 8 nuppu, millel Siiri ja tema sõbrad saavad seista. Nupu peal seismine saadab elektrivoolu juhtmesse. Need juhtmed läbivad kolmnurkseid ja ruudukujulisi kaste ning viivad lõpuks lambini.
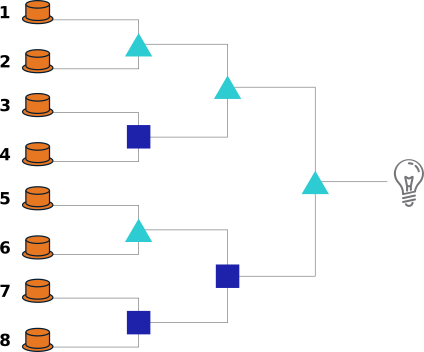
Koprad võidavad mängu, kui nad suudavad lambi sisse lülitada.
Millistel nuppudel peaksid Siiri ja ta sõbrad seisma, et lamp põlema hakkaks?
(Sisesta nuppude numbrid kasvavas järjekorras ja ilma muude märkideta, näiteks 1458. Kui võimalikke lahendusi on mitu, sisesta ükskõik milline neist.)
[Tekstikast]
Õigeid vastuseid on selles ülesandes tervelt 16 tükki: 12356 või 12456 või 1237 või 1247 või 12357 või 12457 või 12367 või 12467 või 1238 või 1248 või 12358 või 12458 või 12368 või 12468 või 1235678 või 1245678.
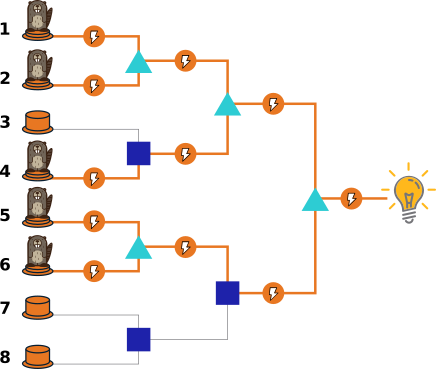
Hea lähenemine sellele ülesandele on töötada tagurpidi. Skeemi lõpus olev lamp on ühendatud kolmnurgast tuleva juhtmega. Selleks, et selles juhtmes oleks vool, peab ka mõlemas kolmnurka viivas juhtmes olema vool.
Need juhtmed on ühendatud kolmnurga ja ruuduga. Teame, et kolmnurgas peab olema vool, seega peab ka mõlemas sellega ühendatud juhtmes olema vool. Teame ka, et ruudus peab olema vool, seetõttu peab ühes sellega ühendatud juhtmetest olema vool ja teises mitte.
Veergude 1 ja 2 puhul vaatame ülemises ja alumises pooles olevaid juhtmeid eraldi. Ülemise poole jaoks peavad mõlemad 2. veerus olevad juhtmed olema voolu all, seetõttu tuleb vajutada 1. veeru mõlemat ülemist nuppu ja täpselt ühte alumisest kahest nupust.
Alumise poole jaoks peab üks ruutu viivatest juhtmetest olema voolu all ja teine mitte. Seega peab kas sinna viiv kolmnurk olema voolu all ja ruut mitte või vastupidi. Selleks on mitu võimalust, ülaltoodud lahendus näitab ühte võimalikku lähenemisviisi. Selle lahenduse puhul on kolmnurk voolu all (ja selle jaoks tuleb vajutada mõlemat nuppu), see aga tähendab, et ruut peab olema ilma vooluta (seega kas mõlemad nupud alla vajutatud või mõlemad nupud üleval, praegusel juhul mõlemad üleval).
Selles ülesandes võivad juhtmed olla voolu all või mitte. Arvutiteadlased nimetavad selliseid andmeid, mis võivad olla ainult kahes erinevas olekus, binaarseteks. Teised näited binaarsuse kohta on kahendarvud (mis kasutavad ainult numbreid 0 ja 1) või kontrollimine, kas mingi tingimus kehtib või mitte, või kontrollimine, kas mingit väide on õige või vale.
Binaarsed andmed on arvutite toimimise seisukohalt väga olulised. Arvutid koosnevad miljarditest pisikestest lülititest, mida nimetatakse transistorideks. Need transistorid võivad olla välja või sisse lülitatud ning kõik, mida arvuti saab teha, on muuta transistoride olekuid nende kahe oleku vahel.
Transistoridest koostatakse arvutis loogikalülisid, mida selles ülesandes näeme. Kolmnurki, mis lülituvad sisse ainult siis, kui mõlemad sissetulevad juhtmed on voolu all, nimetatakse "JA"-lülideks (ingl AND gate), ning ruute, mis lülituvad sisse ainult siis, kui täpselt üks sissetulev juhe on voolu all, nimetatakse "välistav VÕI"-lülideks (ingl XOR gate). Need on vaid kaks võimalikku, tegelikult on loogikalülide tüüpe kasutusel rohkem.
Teine koht, kust leiame loogikatehteid, on arvutiprogrammid. Mõnikord peab programm tegema otsuseid selle kohta, mida edasi teha, lähtudes sellest, kas üks asi (või mõnikord palju asju) on varem juhtunud. Nende otsuste tegemisel mitme erineva tingimuse põhjal kasutatakse loogikatehteid, nende hulgas ka AND- ja XOR-tehet.

Arvuti ekraanil on joonistus konnast. Konna värv pole teada.

Värvi muutmiseks on meil olemas neli programmi, kuid me võime käivitada neist vaid ühe. Tahame olla kindlad, et programmi töö lõppedes on konn kindlasti roheline sõltumata sellest, mis värvi ta oli alguses.
Millise programmi peaksime käivitama?
[Raadionupud]
A.
Kui konn on punane, siis värvi ta roheliseks, muidu värvi ta kollaseks.B.
Kui konn on kollane, siis värvi ta punaseks, muidu värvi ta roheliseks.C.
Kui konn on kollane, siis värvi ta punaseks.
Kui konn ei ole kollane, siis värvi ta roheliseks.D.
Kui konn on punane, siis värvi ta roheliseks.
Kui konn ei ole punane, siis värvi ta kollaseks.Õige vastus on: C.
Õige vastus on C, kuna teise käsu täitmisel on kindlasti tõene selle tingimus: kui alguses oli konn kollane, siis pärast esimese käsu täitmist on see punane ja seega (kuna ta teise käsu täitmise alguseks pole mitte mingil juhul kollane) värvitakse ta roheliseks.
Programmi A käivitamisel värvitakse konn lõpus roheliseks ainult siis, kui ta oli algselt punane, kõigil muudel juhtudel värvitakse ta kollaseks.
Kui käivitame programmi B, muutub konn roheliseks juhul, kui see alguses ei olnud kollane (sel juhul on ta lõpuks punane).
Kui käivitate programmi D, värvitakse konn igal juhul kollaseks.
Programmeerides (kui rääkida imperatiivsetest programmeerimiskeeltest) võime kirjutada rea tingimuslauseid, mida täidetakse antud järjekorras. Tingimuslaused on kujul "kui C, siis A, muidu B" (ingl "if C then A else B") või ka ainult "kui C, siis A" (ingl "if C then A"), diagrammil näevad need välja selliselt:
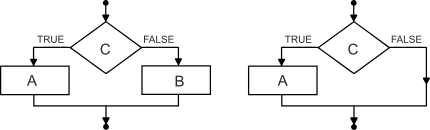
Paneme tähele, et kaks programmi
kui C, siis A, muidu Bja
kui C, siis A
kui mitte C, siis Bpole üldiselt ekvivalentsed ehk neil pole alati sama tähendus. Nimelt võib teisel juhul (kui tingimust C kontrollitakse kaks korda) käsu A täitmine muuta süsteemi olekut selliselt, et tingimus C muutub vääraks, seega käivitatakse nii käsk A kui ka käsk B. Esimese variandi puhul täidetakse kindlasti ainult üks kahest käsust (A või B). Sellist erinevust näeme ka vastusevariantide B ja C võrdlemisel.

Tiina alustas kahest kujundist: ringist ja ruudust.

Neid kasutades moodustas ta südame:

Tiina kasutas südame moodustamiseks ainult selliseid operatsioone:
Millist järgnevatest käsujadadest võis Tiina südame koostamiseks kasutada?
[Raadionupud]
A. Dubleeri ring. Pööra ruutu. Liiguta ringi. Liiguta ringi.
B. Dubleeri ruut. Pööra ruutu. Liiguta ruutu. Liiguta ringi.
C. Dubleeri ring. Pööra ringi. Liiguta ringi. Liiguta ruutu.
D. Liiguta ringi. Liiguta ringi. Dubleeri ring. Liiguta ruutu.
Õige vastus on: A.
Ruutu peab pöörama nii, et nurk oleks suunaga alla. Seda tehakse ainult variantides A ja B, seega saab ainult üks neist olla õige vastus. Samuti näeme, et südame moodustamiseks on vaja kahte ringi. Variant B ei saa olla õige, sest ringi ei dubleerita, seega jääb alles ainult variant A.
Allolevatel joonistel näeme variandi A järgi tehtud operatsioonide tulemusi, seega A on sobiv.
| Operatsioon | Tulemus |
|---|---|
| Dubleeri ring |  |
| Pööra ruutu |  |
| Liiguta ringi |  |
| Liiguta ringi |  |
Teine võimalik operatsioonide jada südame saamiseks on: Dubleeri ring. Pööra ruutu. Liiguta ruutu. Liiguta ruutu.
Kui loote pilte graafikaredaktoriga, saate teha erinevaid operatsioone. Antud ülesande puhul kasutame südame moodustamiseks selliseid lihtsaid kujundeid nagu ring ja ruut: teeme ringist koopia, pöörame ruutu, liigutame ringi jne. Kui me soovime, et neid operatsioone teeks arvuti, peame lisama ka vajalikku infot: kuhu tuleb ring liigutada ja kui palju ruutu pöörata.
Vastusevariantides toodud jadad on puudulikud kirjeldused selle kohta, mida teha. Arvutiteadlased ütlevad, et need on käskude üldistused. Nad annavad ettekujutuse, mida teha, kuid nad ei selgita seda piisavalt üksikasjalikult, et programm saaks töötada. See on kasulik, sest üksikasjade ignoreerimine võimaldab meil keskenduda olulisele. Tarkvara arendamist alustatakse sageli üldistustega, et programmi põhiidee välja mõelda ja alles hiljem puuduvad detailid lisada.

Järgnevas tekstilõigus on tühikud tähistatud märgiga '·' ja lõiguvahetused märgiga '¶'. Tähistamata reavahetused on tekstitöötlusprogrammi poolt automaatselt lisatud.
§·1.·Eesti·on·iseseisev·ja·sõltumatu·demokraatlik·vabariik·,kus·kõrgeima·
riigivõimu·kandja·on·rahvas.·Eesti·iseseisvus·ja·sõltumatus·on·aegumatu·
ning·võõrandamatu.¶
§·2.·Eesti·riigi·maa-ala,territoriaalveed·ja·õhuruum·on·lahutamatu·ja·
jagamatu·tervik·.·Eesti·on·riiklikult·korralduselt·ühtne·riik,·mille·
territooriumi·haldusjaotuse·sätestab·seadus.¶Mitmes sõnavahes on selle teksti vormistamisel tühikuid valesti kasutatud?
(Kui ühes sõnavahes on mitu viga, lugeda seda ainult üks kord.)
[Täisarv]
Õige vastus on: 3.
Esimene viga on 'vabariik·,kus', kus tühik peaks olema koma järel, mitte selle ees.
Teine viga on 'maa-ala,territoriaalveed', kus peaks koma järel olema tühik.
Kolmas viga on 'tervik·.·Eesti', kus punkti ees ei peaks tühikut olema.
Lisaks sellele, et kirjavahemärkide valesti kasutamine on eksimine õigekirjareeglite vastu, võib see tekstide arvutis töötlemisel kaasa tuua ka ebameeldivusi automaatse reapoolitusega. Kui jätta koma või punkti järele tühik panemata, ei saa tekstitöötlusprogramm sellesse kohta vajadusel reavahetust lisada; sellega võib kannatada teksti joondamine. Kui panna tühik koma või punkti ette, võib tekstitöötlusprogramm sinna automaatse reavahetuse lisada ja nii satub kirjavahemärk üksikuna järgmise rea algusse; ka see näeb inetu välja.
Õigekirja seisukohalt võib arutada, kas 'vabariik·,kus' on üks viga (tühik ja koma on omavahel vales järjekorras) või kaks viga (koma ees liigne tühik, koma järel vajalik tühik puudu). Selleks, et oleks üheselt selge, ongi ülesandes küsitud vigade arvu asemel nende sõnavahede arvu, kus on midagi valesti. Samasugust täpsust on vaja paljudes olukordades, kus erinevad osapooled (olgu inimesed või arvutid) peavad mingit reeglit kõik ühtemoodi mõistma — näiteks siis, kui eesti keele eksami etteütluse osas on hindamine määratud vigade arvuga.

Vaatame järgmist tabelarvutuse töölehte, mille mõnes lahtris on arvud ja mõnes valemid:

Töölehe funktsioon SUM arvutab antud piirkonna lahtrites olevate väärtuste summa, funktsioon MAX aga leiab antud piirkonna lahtrites olevatest väärtustest maksimaalse. Lahtrite piirkonnad on antud oma vasakpoolseima ülemise ja parempoolseima alumise lahtriga.
Milline väärtus tuleb tabeli lahtrisse C3?
[Täisarv]
Õige vastus on: 21.
Lihtne viis vastuse leidmiseks on kõigi lahtrite väärtused välja arvutada. Nii saame
B2 = SUM(A1:A3) = A1+A2+A3 = 1+6+7 = 14
B3 = SUM(A2:A4) = A2+A3+A4 = 6+7+8 = 21
B4 = SUM(A3:A5) = A3+A4+A5 = 7+8+4 = 19
C3 = MAX(A1:A3) = MAX(14;21;19) = 21Teine võimalus oleks panna tähele, et B3 väärtus erineb B2 väärtusest selle poolest, et summast jääb välja 1, aga lisandub 8; seega peab B3 väärtus olema suurem. Analoogiliselt saame, et B3 väärtus on suurem ka B4 omast. Seega on just B3 väärtus see maksimum, mille lahtris C3 olev valem valib ja võime piirduda ainult selle ühe summa väljaarvutamisega.
Tabelarvutuse töölehtede valemid võimaldavad korduvaid arvutusi automatiseerida ning sellega kasutajate aega kokku hoida ja käsitsi arvutamisest tulenevate vigade arvu vähendada.
Ka tabelarvutussüsteemid püüavad tehtava töö mahtu optimeerida. Kui me mingi lahtri väärtust muudame, siis arvutab süsteem üle ainult nende valemite väärtused, mis sellest lahtrist sõltuvad (ja siis need valemid, mis muutunud väärtustest sõltuvad jne). Meetod on küll erinev sellest, mida me eespool summade väljaarvutamise vältimiseks kasutasime, aga eesmärk on sama: teha vähem tühja tööd. Arvutid arvutavad küll kiiresti, aga väga suurte paljude valemitega töölehtede puhul on kokkuhoid ikka vajalik.

Ants lõi uue viirusetõrjeprogrammi, mis suudab avastada ohtlikku tarkvara. See kontrollib arvutisse lisatavaid programme, keskendudes analüüsil neljale punktile:
Kui viirusetõrjeprogramm leiab kontrollitava programmi koodist vähemalt kaks ülaltoodud tegevust, loetakse programm ohtlikuks ja pannakse karantiini.
Milline allolevatest programmidest pannakse karantiini?
[Raadionupud]
A. loe fail dokumendikaustast; prindi fail; salvesta fail dokumendikausta; saada fail e-postiga.
B. loe fail dokumendikaustast; prindi fail; lisa fail automaatkäivitusse.
C. loe fail süsteemikaustast; prindi fail; salvesta fail dokumendikausta; saada fail e-postiga.
D. loe fail automaatkäivituse kaustast; prindi fail; salvesta fail dokumendikausta; saada fail e-postiga.
Õige vastus on: C.
Nagu allpool näha, sisaldavad variandid A, B ja D ainult üht toodud punktidest (need on esile toodud poolpaksus kirjas), C puhul on ohtlikke käske kaks.
A. loe faili dokumendikaustast; prindi fail; salvesta fail dokumendikausta; saada fail e-postiga.
B. loe fail dokumendikaustast; prindi fail; lisa fail automaatkäivitusse.
C. loe fail süsteemikaustast; prindi fail; salvesta fail dokumendikausta; saada fail e-postiga.
D. loe fail automaatkäivituse kaustast; prindi fail; salvesta fail dokumendikausta; saada fail e-postiga.
Turvatarkvara on välja töötatud arvutit kahjustada võivate ohtlike programmide tuvastamiseks ja eemaldamiseks. Mõnikord on võimalik ohtlik programm (näiteks viirus) tuvastada selles esineva kindla koodilõigu järgi, aga sageli kasutatakse tarkvara ohtlikkuse hindamiseks ligikaudseimaid meetodeid.
Mõnikord kasutab turvatarkvara "liivakasti" (ingl sandbox) ehk kaitstud keskkonda, kus ta kahtlusaluse programmi käivitab ja selle tegevuse tagajärgi kontrollib. Sageli kasutavad viirusetõrjeprogrammid ka tehisintellekti võimalusi, et "õppida", laiendades nii oma andmebaasi ning leides viiruseid tänu sellele kergemini ja kiiremini.

Siimule meeldib teha ruudulisele paberile väikesi pilte suurusega 4x4 ruutu. Ta kirjutab iga pildi jaoks 8-kohalise kahendkoodi ning jagab selle pooleks: esimesed 4 numbrit kirjutab ta paberi ülemisse äärde vasakult paremale ja viimased 4 vasakusse äärde ülalt alla.
Seejärel kasutab ta järgmisi reegleid:
 
|
 
|
Näiteks koodi 10100101 järgi joonistab Siim sellise pildi:
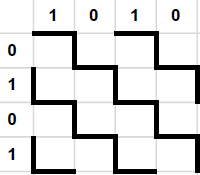
Järgmine pilt on aga joonistatud koodi 10110110 põhjal:
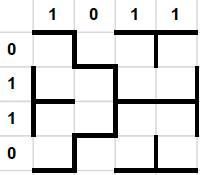
Millise järgnevatest piltidest joonistas Siim koodi 10011000 järgi?
[Raadionupud]
A. 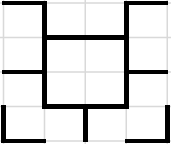
B. 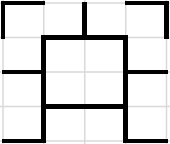
C. 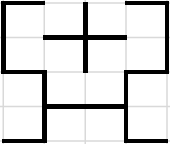
D. 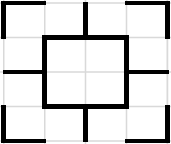
Õige vastus on: B.
Kuigi koodi 10011000 järgi õige pildi tervikuna valmis joonistamine viib õige vastuseni, saab lahenduse leida ka kiiremini. Selleks kontrollime, millised peaksid iga vastusevariandi puhul olema tabeli vasakus ääres ülalt alla olevad koodid:
Nagu näha, on ainult variant B kooskõlas koodi 10011000 tagumise poolega 1000.
Nüüd saame täiendavalt kontrollida, kas see vastus on õige, kontrollides koodi esimest poolt. Variandi B veerud algavad joonega, vahelejätmisega, vahelejätmisega ja joonega ehk vastav kood oleks 1001. Seetõttu on B tõepoolest õige vastus.
Arvusüsteemi, mis kasutab ainult numbreid 1 ja 0, nimetatakse kahendsüsteemiks. Arvutite toimimise aluseks on kahendarvud. Arvutite kõige väiksemat infoühikut nimetatakse bitiks (ingl binary digit ~ bit), mis on kahe võimaliku väärtusega olek (1 või 0). Kaheksa bitti (nagu on näha ka antud küsimuses) annavad suurema infoühiku nimega bait (ingl byte). Traditsiooniliselt vastab üks bait arvutis ühele tekstisümbolile.
Kuigi kahendarvu saab esitada kaheksakohalise arvuna (nt 10011000), võib seda esitada ka pildina, mis järgib reegleid, nagu on näidatud selles ülesandes. See on näide andmete esitamise, salvestamise, töötlemise ja visualiseerimise ühest võimalikust viisist. Arvutiteadlased valivad selleks sageli erinevaid võimalusi, mõnikord on andmete visuaalne esitus kasutajale mugavam kui esitus tekstina, mõnikord vastupidi.

Ahelkood on kokkuhoidlik viis must-valgel pildil olevate kontuuride (piirjoonte) esitamiseks. Põhimõte on valida üks must piksel ja salvestada igal sammul suund liikumiseks järgmise musta pikslini kontuuri päripäeva (kellaosuti liikumise suunas) läbimisel.
Suunad on tähistatud numbritega selliselt:
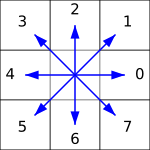
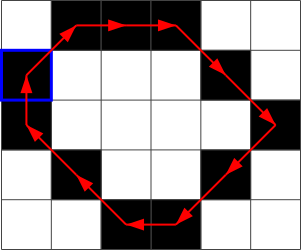
Näiteks kui valime alloleval pildil esimeseks sinise raamiga tähistatud piksli, saame edasi liikuda punaste nooltega näidatud suundades ja tulemuseks on ahelkood 1, 0, 0, 7, 7, 5, 5, 4, 3, 3, 2.
Vaatame nüüd sellist pilti:

Milline järgmistest ei ole selle pildi ahelkood?
[Raadionupud]
A. 1, 1, 1, 0, 7, 7, 7, 6, 5, 5, 5, 4, 3, 3, 3, 2
B. 7, 6, 5, 5, 5, 5, 4, 3, 3, 2, 1, 1, 1, 1, 0, 7
C. 5, 5, 5, 4, 3, 3, 3, 2, 1, 1, 1, 0, 7, 7, 7, 6
D. 3, 3, 2, 1, 1, 1, 0, 7, 7, 7, 6, 5, 5, 5, 4, 3
Õige vastus on: B.
Järgnevad joonised illustreerivad vastusevariantides olevate ahelkoodide saamist:
A. 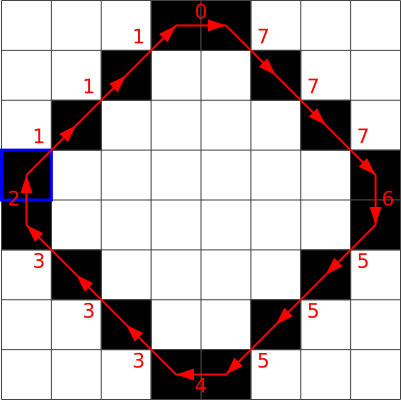 B.
B. 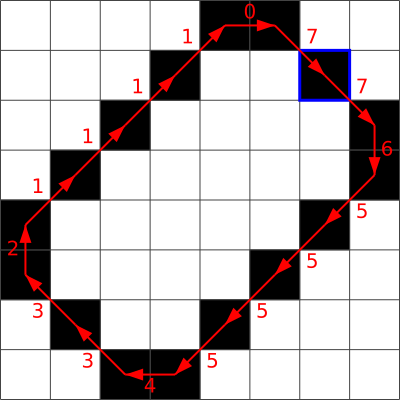
C. 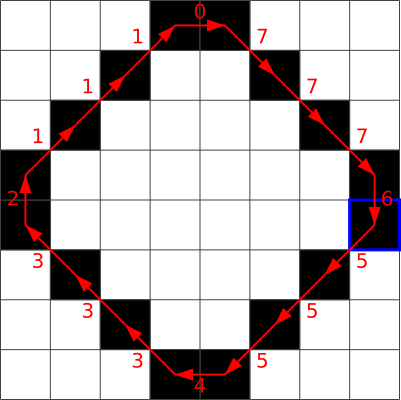 D.
D. 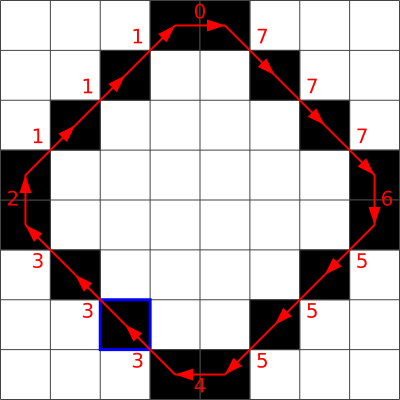
Ahelkood on üks meetod objektide esitamiseks nende kontuuride abil. Ahelkood on määratud stardipiksli määramisega ja suunavektorite jadaga vastavalt sellele, kas igal sammul suundutakse kontuuri järgmise musta pikslini vasakul, paremal, üleval, all või diagonaalis. Ahelkoodi eeliseks on vajaliku info säilitamine ja samas andmemahu väga suur kokkuhoid. Esimesena esitles ahelkoodi ideed Freeman 1961. aastal ning seepärast on see tuntud ka kui Freemani ahelkood (ingl Freeman Chain Code, FCC).
Ahelkoodi üks kasutusala on numbrituvastus. Esiteks võimaldab see kood objekte kompaktselt esitada, teiseks on ahelkoodide võrdlemine lihtsam kui piltide võrdlemine. Lisaks sellele on ahelkoodist võimalik välja lugeda ka kujutatava objekti üksikuid omadusi. Ahelkoodid esindavad kadudeta tihendamist ja säilitavad kogu info, mis on vajalik kiireks ja efektiivseks mustrite analüüsiks.
Copyright © 2022 Bebras – International Challenge on Informatics and Computational Thinking.
Licensed under Creative Commons Attribution-ShareAlike 4.0 International License.
Flag icons by GoSquared.