

Lossis nimega Müsteeria elab võlur. Võlur võib kas muuta ennast haldjaks või tekitada haldja enda kõrvale paremale. Haldjas võib muutuda võlujoogiks (vasakul) ja draakoniks (paremal) või võlujoogiks (vasakul), võluriks (keskel) ja draakoniks (paremal).
Järgmine tabel näitab nende võimalike teisenduste tulemusi:
| Enne | Pärast |
|---|---|
 |
 |
 |
  |
 |
  |
 |
   |
Need maagilised muutused võivad toimuda kuitahes palju kordi ja mistahes järjekorras: iga võlur ja iga haldjas võivad igal ajal muutuda.
Millist järjekorda ei ole võimalik Müsteerias saada, kui alustada ühest võlurist?
[Raadionupud]
A. 




B. 







C. 





D. 



Õige vastus on: B.
Nummerdame maagilised teisendused järgmiselt:
| Number | Enne | Pärast |
|---|---|---|
| 1 |  |
 |
| 2 |  |
  |
| 3 |  |
  |
| 4 |  |
   |
Valik A on võimalik, kui alustame ühest võlurist ja rakendame teisendusi 1, 4, 2 ja 3.
Valik C on võimalik, kui alustame ühest võlurist ja rakendame teisendusi 2, 2, 3, 4 ja 1.
Valik D on võimalik, kui alustame ühest võlurist ja rakendame teisendusi 2, 1, 3 ja 3.
Üks kiire viis tuvastada, et variant B pole võimalik, on tähele panna, et teisendusreeglid loovad alati samaaegselt nii võlujoogi kui ka draakoni. Seetõttu peab Müsteerias olema võlujookide arv alati võrdne draakonite arvuga, aga variandi B puhul see nii ei ole.
Maagilisi teisendusi võib käsitleda kui reeglite kogumit, mida kasutatakse Müsteeria objektidest mustrite loomiseks.
Arvutiteaduses on kontekstivaba grammatika tööriist, mida saab kasutada mustreid genereerivate reeglite kirjeldamiseks. Kontekstivabad grammatikad suudavad kirjeldada nii formaalseid kui loomulikke keeli: korduvalt grammatikareegleid rakendades saame me genereerida sõnu, mis moodustavadki keele.
Selles ülesandes pidime me sisuliselt otsustama, milline antud sõnadest ei kuulu "Müsteeria keelde".

Jõe ääres on rida palke, kõik erineva suurusega. Henriku ülesanne on panna palgid suuruse järjekorda nii, et kõige väiksem oleks rea vasakus ja kõige suurem rea paremas otsas. Henrik kõnnib mööda kallast, peatudes alati kahe palgi vahel. Ta võrdleb nende kahe palgi suurusi ja vajadusel vahetab nende asukohad.
Henrik teab, et sõltumata palkide algsest järjekorrast saab ta need alati õigesti sorteerida järgmisel viisil:
Vaatame, kuidas Henrik sel viisil palke sorteerib:
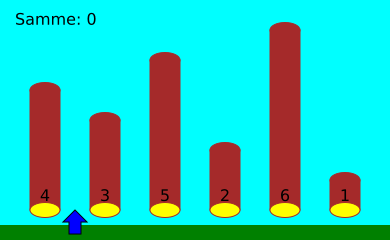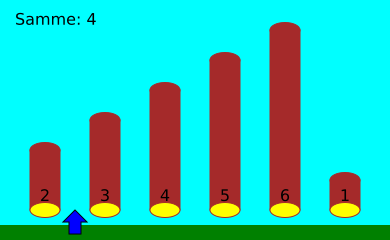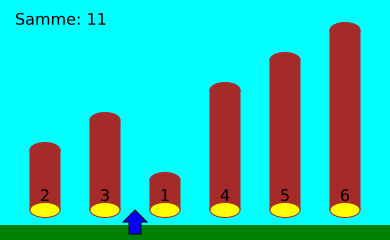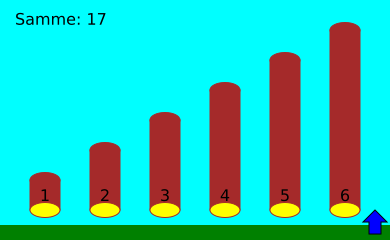
Selles näites peab Henrik astuma vasakule ja paremale kokku 17 korda.
Sammude arv, mida Henrik peab sorteerimisel tegema, sõltub palkide algsest järjekorrast. Kuue palgi korral peab ta halvimal juhul astuma 25 sammu.
Kui palju samme võib Henrikul kuluda 60 palgi sorteerimisel?
[Raadionupud]
A. [0...30]
B. [6...70]
C. [59...300]
D. [59...3600]
Õige vastus on: D.
[0...30] on vale. Isegi parimal juhul, kui palgid on juba alguses õiges järjekorras, peab Henrik rea lõppu jõudmiseks astuma 59 sammu, mida on rohkem kui 30.
[6...70] ja [59..300] on samuti valed. Selle tõestamiseks peame uurima halvimat juhtu, kui palgid on algselt vajalikule vastupidises järjekorras. Sel juhul jõuab Henrik k-ndal positsioonil oleva palgini ja liigutab selle esimesse ehk vasakpoolseimasse positsiooni, seejärel läheb ta positsioonil k+1 oleva palgi juurde. Nii teeb Hendrik k-ndal positsioonil oleva palgi puhul k–2 sammu selleni jõudmiseks ning k–2 sammu selle viimiseks rea algusesse. Seega kulub tal kõigi palkide peale kokku 2·(0+1+2+...+58) sammu. Lõpuks kulub tal veel 59 sammu rea lõppu jõudmiseks. Sammude summa on täpselt 59^2=3481 ning see arv ei kuulu kumbagi neist kahest lõigust.
[59...3600] on õige. Selle nägemiseks peame tõestama, et väidetav halvim juhtum on tõesti halvim. Kui Henrik jõuab k-ndal positsioonil oleva palgi juurde, on kõik sellest vasakul olevad palgid juba omavahel õigesse järjekorda sorteeritud, nii et tal on vaja ainult uus palk eelmiste seas õigesse kohta panna. Selleks kulub tal aga seda rohkem samme, mida kaugemale vasakule see palk viia tuleb. Seejärel läheb ta positsioonil k+1 oleva palgi juurde, kus kordub sama loogika. Seega tõesti on halvim juht see, kui iga järgmine palk tuleb viia rea vasakusse otsa.
Sorteerimine ehk jadas olevate objektide kindlasse järjekorda paigutamine on arvutiteaduse klassikaline ülesanne. Kõige sagedamini kasutatavad järjestused on arvuline järjekord (arvude jaoks) ja tähestikuline järjekord (tekstide jaoks). Efektiivne järjestamine on oluline paljude teiste algoritmide (nt otsimisalgoritmide) jaoks, mis nõuavad järjestatud sisendandmeid. Samuti võib järjestamine olla kasulik andmete normaliseerimisel ja inimloetava väljundi loomisel.
Üks tuntud sortimisalgoritme on nn päkapikumeetod (ingl gnome sort). See on lihtne ja opereerib korraga ühe jadaelemendiga, viies elemendi õigesse kohta elementide vahetamiste abil. Päkapikumeetodi (mida on samuti nimetatud rumalaks sorteerimiseks) pakkus välja Sharifi Tehnikaülikooli arvutiteaduse professor Hamid Sarbazi-Azad 2000. aastal.
Algoritmist rääkides tuleb alati mõelda, kui kiire see on, st millist operatsioonide arvu see nõuab sõltuvalt elementide arvust. Kui meil on N palki, kulub nende järjestamiseks päkapikumeetodil halvimal juhul ligikaudu N2 operatsiooni. Arvutiteaduses nimetatakse seda ruutkeerukuseks. Ülejäänud vastused selles ülesandes esindavad teisi võimalikke suhteid: konstantne keerukus [0..30] jaoks, lineaarne keerukus [6..70] jaoks ja lineaar-logaritmiline keerukus [59...300] jaoks.

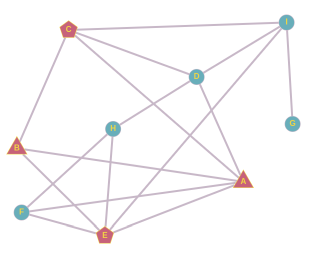
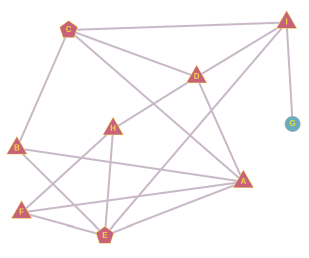
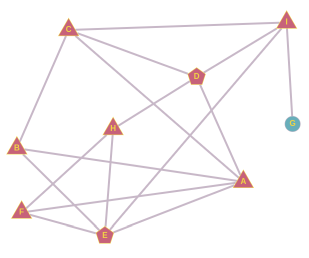
Ühe klassi õpilased suhtlevad oma klassikaaslastega vastavalt joonisele. Näiteks õpilane H suhtleb päeva jooksul ainult D, E ja F-ga.
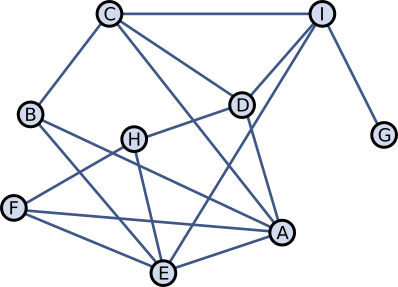
Esmaspäeval tuli tööle uus matemaatikaõpetaja, keda kaks õpilast hakkasid tema soengu tõttu kohe kutsuma Miss Infinityks. Hüüdnimi levis õpilaste hulgas nii, et iga õpilane, kelle vestluskaaslastest rohkem kui pooled seda kasutasid, hakkas ka ise järgmisel koolipäeval uut õpetajat sel viisil hüüdma. Varsti kasutasid uut hüüdnime juba kõik klassi õpilased.
Kes olid need kaks õpilast, kellest hüüdnimi alguse sai?
(Kirjuta nende kahe õpilase tähised ilma muude märkideta, näiteks AB. Kui võimalikke lahendusi on mitu, sisesta ükskõik milline neist.)
[Tekstikast]
Õige vastus on: CE või DE.
Esiteks paneme tähele, et hüüdnime levima hakkamiseks peab kahel hüüdnime kasutusele võtnud õpilasel olema mõni ühine sõber, kellel on kokku täpselt kolm sõpra. Kui ühisel sõbral on rohkem sõpru, pole kaks hüüdnime leiutajat nende hulgas enamuses. Kui ühisel sõbral on kaks sõpra, on need leiutajad ise ja siis hüüdnimi selle ühise sõbra kaudu kellelegi edasi ei levi. Täpselt kolme sõbraga on B, F ja H.
B sõpradest saame moodustada kolm paari: A ja C, A ja E, C ja E. Kui hüüdnime leiutaks A ja C, võtaks B selle küll järgmisel päeval kasutusele, aga pärast seda see edasi ei leviks. Kui hüüdnime leiutaks A ja E, võtaks selle järgmisel päeval kasutusele B ja F ning ülejärgmisel päeval H, aga rohkem see ei leviks. Kui hüüdnime võtaks kasutusele C ja E, leviks see nii:
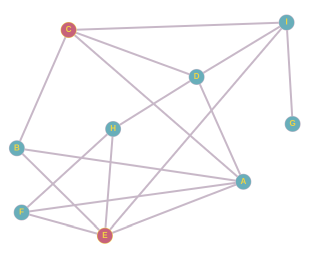
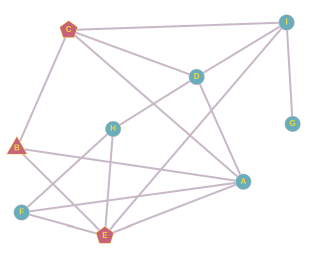
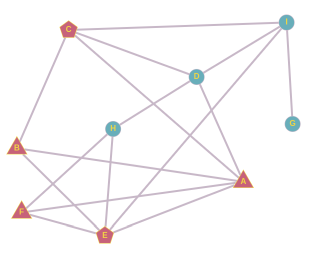
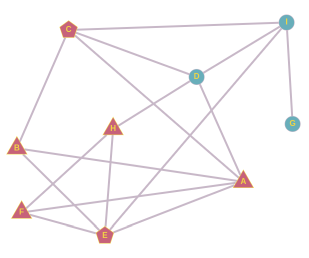
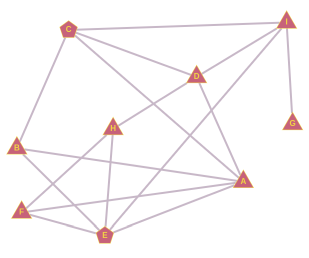
Sarnaselt B juhuga saame F sõpradest paarid A ja E, A ja H, E ja H. Paari A ja E oleme juba analüüsinud. Kui hüüdnime leiutaks A ja H, võtaks selle järgmisel päeval kasutusele F, siis E ja siis B, aga edasi see ei leviks. Kui hüüdnime leiutaks E ja H, võtaks selle järgmisel päeval kasutusele F ja sellega asi lõpekski.
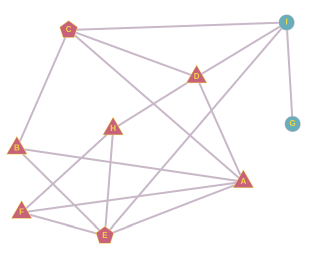
H sõpradest saame paarid D ja E, D ja F, E ja F. Kui hüüdnime leiutaks E ja F või D ja F, lõpeks selle levik jälle H juures. Kui hüüdnime võtaks kasutusele õpilased D ja E, leviks see nii:
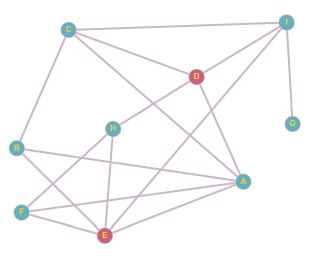
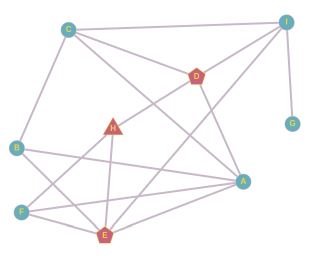
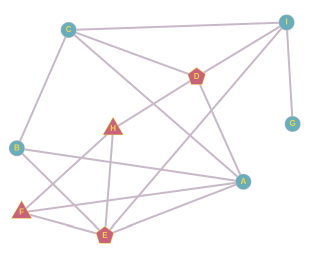
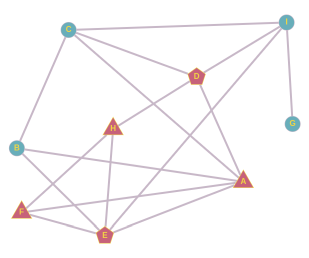
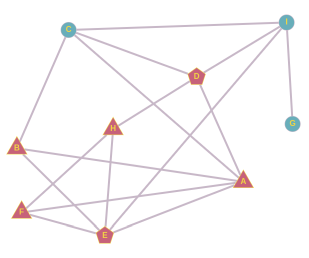
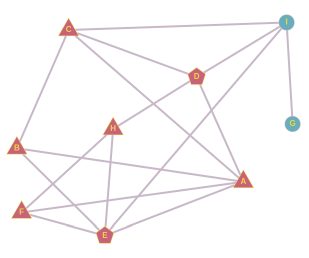
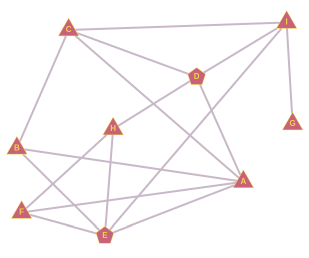
Sellega oleme kõik võimalused ammendanud ja seega vastus on CE või DE.
Sotsiaalvõrgustikud mängivad info, ideede ja seisukohtade levitamisel suurt rolli. Mõte, mis ilmub sotsiaalvõrgustikku, kas levib kiiresti või kaob. Info sotsiaalvõrgustikes levimise kiiruse uurimine on väga populaarne suund informaatikas ja selle kiiruse suurendamine on kujunemas omaette oluliseks haruks reklaamimaailmas.
See ülesanne keskendub nn. lävendimudelile (ingl threshold model), milles igal isikul on lävend ehk kontaktide hulk, mis peab olema aktiivne (praegusel juhul tähendab see uue hüüdnime kasutamist), et ka isik ise muutuks aktiivseks (ehk hakkaks seda hüüdnime kasutama).

Kopra Pagariäris müüakse küpsiseid karpides, et inimestel oleks lihtsam neid teistele kinkida. Kasutatakse kahte tüüpi karpe: ühte mahub täpselt neli küpsist, teise seitse küpsist.
Pagariäri pannile mahub kuni 100 küpsist. Mõnikord küpsetatakse sellel küpsiseid selline arv, et neid ei saa nelja ja seitset küpsist mahutatavatesse karpidesse pakkida ilma, et mõni küpsis üle jääks. Näiteks ei saa sellistesse karpidesse täpselt pakkida 3 või 5 küpsist; ka mõned teised küpsisehulgad ei sobi.
Milline on suurim arv küpsiseid, mida saab sellel pannil küpsetada, aga mida ei saa nendesse karpidesse pakkida ilma, et mõni küpsis üle jääks?
[Täisarv]
Õige vastus on: 17.
Etteantud karpidesse saab pakkida 4, 7, 8, 11, 12, 14, 15, 16, 18, 19, 20, 21 jne küpsist. Kui meil on neli järjestikust arvu, mida saab pakkida (näiteks 18 kuni 21), siis kõik suuremad arvud saame pakkida, liites mõnele eelnevatest kombinatsioonidest piisava hulga 4-küpsiselisi karpe (7-küpsiseliste karpidega saame kuluvate karpide arvu vähendada, aga põhimõttelist "saab / ei saa" otsust see enam ei mõjuta). Suurim arv, mida ei saa nende karpidega kombineerida, on seega 17.
Mündiprobleem (ehk Frobeniuse probleem) on matemaatiline ülesanne, milles otsitakse suurimat summat (Frobeniuse arv), mida antud nimiväärtustega müntidega maksta ei saa. Kui meil on münt väärtusega 1, pole probleemi ühegi arvuga, kuid kui jätame selle mündi välja, siis mõnda summat ei saa enam täpselt maksta. Kui meil on mündid ainult kahe väärtusega A ja B, siis selle komplekti Frobeniuse arv on A·B–A–B.
Suvalise arvu nimiväärtuste jaoks nii lihtsat valemit ei ole, kuid on olemas algoritmid. Näiteks saab kasutada dünaamilist plaanimist: kõigepealt eeldame, et antud müntidega on võimalik maksta ainult summat 0, seejärel vaatame iga järgmise summa X puhul, kas leidub selline nimiväärtus Y, et summa X–Y on makstavate hulgas. Kui selline Y leidub, lisame ka X makstavate summade hulka.

Droon stardib näidatud ruudustiku mõnes valges lahtris tabeli servaga paralleelses suunas.

Seejärel külastab droon täpselt kaheksat valget ruutu selliste juhiste järgi:
Mitu võimalikku stardiruutu ruudustikus kokku on?
[Täisarv]
Õige vastus on: 8.
Vastuse leidmiseks paneme esmalt tähele, et olemas on neli sobivat teekonda:
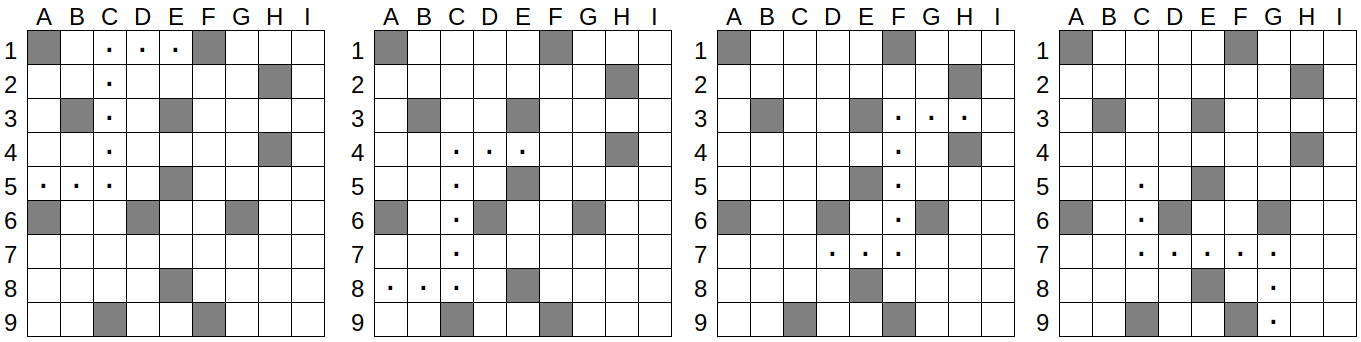
Nende võimaluste leidmiseks on kõige lihtsam alustada viie järjestikuse valge ruudu otsimisega ja seejärel proovida otspunkte laiendada mõlemas suunas. Et olla kindel, peaksime seda tegema süstemaatiliselt, alustades näiteks ruudustiku ülemisest vasakust nurgast ja liikudes alumisse parempoolsesse nurka. Seejuures peame otsima nii horisontaalseid kui ka vertikaalseid viie ruuduga ribasid.
Drooni teekond on sümmeetriline, seega võib droon alustada iga nelja teekonna puhul ükskõik kummast otsast, seetõttu on erinevaid võimalikke stardiruute kaks korda rohkem ehk kaheksa.
Antud probleem on lihtne näide mustrisobitamisest, mis on üks ülesanne pilditöötluse valdkonnas. Siin on probleem määratud malliga (sammud 1–5) ning testruudustiku ehk pildiga, millelt malli otsida. Mallide sobitamisel on palju rakendusi, neid kasutatakse nii näotuvastuses kui meditsiinilise pildimaterjali analüüsimisel. Paljudes mustrisobitusmeetodites on kirjeldatud malli trajektoorina sarnaselt selle ülesande kirjeldusele.

Kuus sõpra valivad, millist seitsmest filmist vaadata. Sõbrad hindavad filme nii:
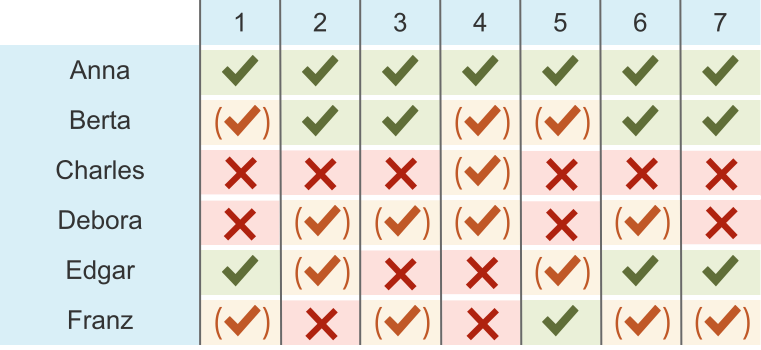
Hinnangud parimast halvimani on järgmised: 


Filmi nimetatakse lemmikfilmiks sellisel juhul, kui kõik sõbrad annavad sellele oma parima hinnangu. Näiteks film nr 1 ei ole lemmikfilm, sest Charles andis oma parima hinnangu filmile 4.
Kui suur on väikseim võimalik arv muudatusi hinnangutes, et üks film saaks lemmikfilmiks?
[Täisarv]
Õige vastus on: 2.
Pole võimalik muuta ainult üht hinnangut, et mõni tabelis olnud filmidest muutuks lemmikfilmiks. Iga filmi jaoks leidus vähemalt kaks sõpra, kes hindasid mingit teist filmi paremaks:
| Film | Muud filmi eelistanute arv |
|---|---|
| 1 | 4: Berta, Charles, Debora ja Franz |
| 2 | 3: Charles, Edgar ja Franz |
| 3 | 3: Charles, Edgar ja Franz |
| 4 | 3: Berta, Edgar ja Franz |
| 5 | 4: Berta, Charles, Debora ja Edgar |
| 6 | 2: Charles ja Franz |
| 7 | 3: Charles, Debora ja Franz |
Nüüd peab veenma Charlesi ja Franzi, et nad kumbki muudaks üht hinnangut nii, et film 6 oleks nende lemmikfilm. Ilmne lahendus ainult kahe muutusega on, et Charles ja Franz võivad parandada oma hinnanguid filmile 6. Aga teise võimalusena võivad nad ka alandada nende filmide hinnangut, millele nad panid parema hinde kui filmile 6, see tähendaks filme 4 (Charles) ja 5 (Franz). Paneme tähele, et teine lahendus ei oleks võimalik, kui ühel (või mõlemal) sõbral oleks rohkem kui üks filmist 6 kõrgemalt hinnatud film.
Kuidas ülesande lahendamiseks vajalikku tabelit koostada?
Üks võimalus on kontrollida iga filmi ja iga sõbra puhul eraldi, kas see sõber on mõnele teisele filmile parema hinnangu andnud. Kuid kas selline algoritm on ka optimaalne? Kui meil on S sõpra ja F filmi, peame vaatama kõiki lahtreid S*F suuruses tabelis ja igaühte neist võrdlema selle sõbra hinnangutega ülejäänud F–1 filmile. Kokku peame niimoodi naiivselt toimetades tegema S·F·(F–1) reitingute võrdlemist.
Tegelikult piisab selleks, et näha, kas ühe sõbra hinnang konkreetsele filmile tekitab probleeme, teadma ainult tema parimat hinnangut. Kui konkreetne hinnang on madalam kui selle sõbra üldine parim, ei saa hinnatud film olla lemmik. See tähendab, et kui me saame kõigepealt teada iga sõbra parimad hinnangud (vaadates läbi F·S reitingut), saame kontrollida kõigi F·S hinnangu puhul, kas need on madalamad kui vaadeldava sõbra parim. Kokkuvõttes tuleb sellise alternatiivse algoritmi puhul koos parimate hinnangute eelarvutusega vaadata läbi 2·F·S hinnangut.
Kui S=6 ja F=7 kulutab esimene algoritm 252 ja teine 84 operatsiooni. Mõlemad algoritmid annavad sama tulemuse, kuid teine on efektiivsem kui esimene.
Arvutiteadlaste üheks põhitegevuseks ongi probleemide lahendamine mitte ainult õigesti, vaid ka võimalikult efektiivselt. Arvutite riistvara läheb küll aina kiiremaks, kui sellest pole palju kasu, kui programmeerijad selle kiiruse kasvu ebaefektiivsete algoritmidega "ära söövad".

Berta küsis oma sõbrannalt Annalt telefoninumbrit. Kuna Anna ei taha, et teised teaksid tema telefoninumbrit, andis ta paberi, kus telefoninumber oli salastatud. Hiljem seletas Anna Bertale, et number on kodeeritud sellisel viisil:
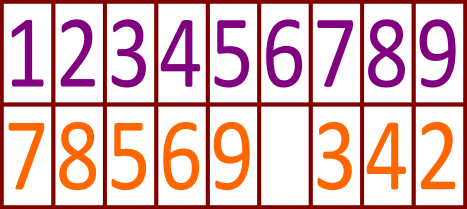
Milline neist on Anna telefoninumber?
[Raadionupud]
A. 123 456 789
B. 785 691 342
C. 173 592 846
D. 173 859 246
Õige vastus on: C.
Kui me järjestame tabeli veerud ümber järgmiste numbrite järgi (nii, et iga number 2. reas on sama nagu järgmise veeru 1. rea number), kuvatakse õige vastus 1. reale.
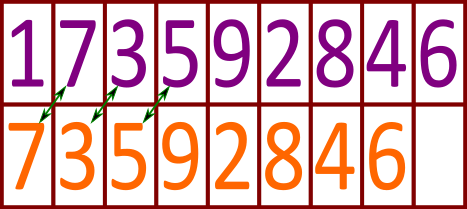
Isikuandmete krüpteerimine on meie elus väga oluline. Keegi ei taha, et teised teaksid tema PIN-koodi või pangakonto parooli, keegi ei soovi, et teised tema kirjavahetust loeksid. Meie kirju, isikuandmeid ja raha pankades tuleb kindlalt hoida. Õnneks oskavad arvutid väga hästi sõnumeid krüpteerida ja arvutiteadlased näevad palju vaeva, et leida uusi võimalusi digiandmete turvamiseks.
Kahjuks pole arvutitele mõeldud krüptoalgoritmid sobivad kasutamiseks, kui asi puudutab infot, mida inimesed peavad paberile kirjutama või paberilt lugema. Sel puhul tuleb leppida vähem arvutusi nõudvate meetoditega, mis pole küll nii turvalised, kuid kaitsevad siiski juhusliku piiluja eest.
Telefoninumbri numbrid salvestasime oma ülesandes erilisel viisil. Selle asemel, et paigutada need telefoninumbris ilmumise järjekorda, oleme lisanud igale neist viite, mis näitab, kus asub järgmine number. Sarnaseid arvutites kasutatavaid struktuure nimetatakse lihtahelateks (ingl linked list) ja neil on mitmeid eeliseid. Kui tahame sellesse loendisse mõnda elementi teiste vahele lisada, ei pea me teisi elemente liigutama, piisab vaid kahe viite muutmisest.

Siim ja Peeter on naabrid: nende tubade aknad on üle tänava teineteise vastas. Iga päev mängivad nad mängu: õhtul enne magamaminekut kirjutavad mõlemad paberile arvu ja kleebivad selle oma aknale. Hommikul vaatavad mõlemad vastasaknal olevat arvu, liidavad selle oma arvule ja kinnitavad uue paberi saadud summaga enda aknale. Võidab see, kelle aknal oleval paberil on lõpuks väiksem arv.
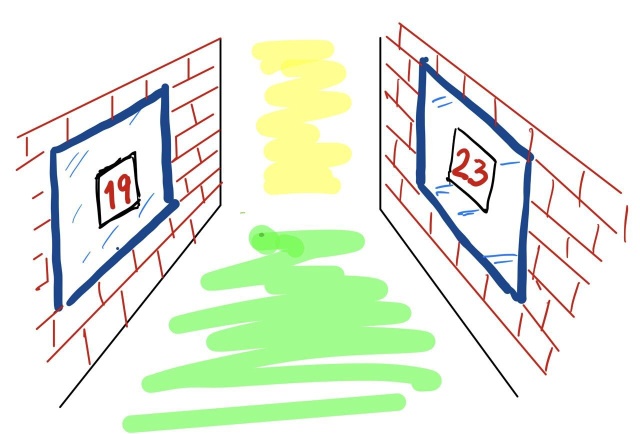
Siim ja Peeter ärkavad erinevatel päevadel erinevatel aegadel. Akendel olevad lõplikud arvud sõltuvad sellest, millal kumbki neist ärkab. Oletame näiteks, et Siim kirjutab enne magamaminekut 19 ja Peeter 23. Kui Siim ärkaks enne Peetrit, asendaks ta oma aknal oleva arvu 19 arvuga 42. Peeter näeks siis arvu 42 ja kirjutaks oma aknale 65. Seega Siim võidaks. Kui mõlemad ärkaksid samal ajal, kirjutaksid nad mõlemad 42 ja mäng lõpeks viigiga.
Oletame nüüd, et Siim kirjutab enne magamaminekut arvu 25 ja Peeter arvu 47.
Milline järgnevatest variantidest ei ole võimalik?
[Raadionupud]
A. Siim kirjutab 72 ja Peeter kirjutab 119, seega Siim võidab.
B. Siim kirjutab 97 ja Peeter kirjutab 119, seega Siim võidab.
C. Siim kirjutab 72 ja Peeter kirjutab 72, seega on mäng viigis.
D. Siim kirjutab 97 ja Peeter kirjutab 72, seega Peeter võidab.
Õige vastus on: B.
Variant B pole võimalik. Kui nad ärkavad samal ajal, kirjutavad nad mõlemad 72. Kui Siim ärkab enne Peetrit, kirjutab Siim 72 ja Peeter 119. Kui Peeter ärkab enne, kirjutab Peeter 72 ja Siim 97. Selleks, et Siim kirjutaks 97 ja Peeter 119, peaks nad mõlemad nägema sõbra summat enne oma arvu uuendamist, aga see pole võimalik.
Paljud arvutisüsteemid toetavad paralleelsust, kui korraga töötab rohkem kui üks protsess. Kui need samaaegsed arvutused muudavad ühiseid muutujaid, peame tagama nende värskenduste õige järjekorra. Näiteks rongipiletite broneerimissüsteemis saab mitu kasutajat korraga pileteid broneerida. Kui vabade kohtade arv on väiksem kui broneerimistaotluste arv, peame tagama, et ühtegi kohta ei broneeritaks topelt. Samaaegsete arvutuste analüüsimine on keeruline, kuna peame uurima kõiki võimalikke järjestusi, milles üksikud protsessid võiksid edeneda.

Arvuti ekraanil on joonistus konnast. Konna värv pole teada.

Värvi muutmiseks on meil olemas neli programmi, kuid me võime käivitada neist vaid ühe. Tahame olla kindlad, et programmi töö lõppedes on konn kindlasti roheline sõltumata sellest, mis värvi ta oli alguses.
Milline programm ei taga, et selle täitmise lõpus oleks konn rohelist värvi?
[Raadionupud]
A.
Kui konn on punane, siis värvi ta kollaseks, muidu värvi ta roheliseks.
Kui konn on kollane, siis värvi ta punaseks.
Kui konn ei ole kollane, siis värvi ta roheliseks.B.
Kui konn on punane, siis värvi ta kollaseks.
Kui konn ei ole punane, siis värvi ta roheliseks.
Kui konn on kollane, siis värvi ta punaseks, muidu värvi ta roheliseks.C.
Kui konn on kollane, siis värvi ta roheliseks.
Kui konn ei ole kollane, siis värvi ta punaseks.
Kui konn on punane, siis värvi ta roheliseks, muidu värvi ta kollaseks.D.
Kui konn on kollane, siis värvi ta roheliseks, muidu värvi ta punaseks.
Kui konn on punane, siis värvi ta roheliseks, muidu värvi ta kollaseks.Õige vastus on: D.
Programmi A käivitamisel on pärast esimese käsu täitmist konn kas kollane või roheline, pärast teise käsu täitmist on ta kas punane või roheline, seega kolmanda käsu täitmisel tingimus "konn ei ole kollane" kehtib ja ta värvitakse roheliseks.
Kui käivitame programmi B, siis teise käsu täitmisel peab kindlasti paika tingimus "konn ei ole punane", seega värvitakse konn roheliseks, mille järel kolmas käsk värvib ta uuesti roheliseks.
Kui käivitame programmi C, siis teise käsu täitmisel peab kindlasti paika tingimus "konn ei ole kollane", seega värvitakse konn punaseks, mille järel kolmandas käsk värvib ta roheliseks.
Kui programmi D täitmise alguses on konn kollane, siis esimese käsu täitmisel värvitakse see roheliseks; selle järel tingimus "konn on punane" ei kehti ja seetõttu saab ta jälle kollaseks värvitud.
Programmeerides (kui rääkida imperatiivsetest programmeerimiskeeltest) võime kirjutada rea tingimuslauseid, mida täidetakse antud järjekorras. Tingimuslaused on kujul "kui C, siis A, muidu B" (ingl "if C then A else B") või ka ainult "kui C, siis A" (ingl "if C then A"), diagrammil näevad need välja selliselt:
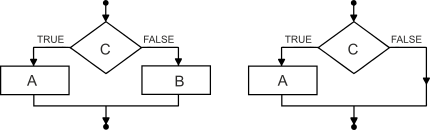
Paneme tähele, et kaks programmi
kui C, siis A, muidu Bja
kui C, siis A
kui mitte C, siis Bpole üldiselt ekvivalentsed ehk neil pole alati sama tähendus. Nimelt võib teisel juhul (kui tingimust C kontrollitakse kaks korda) käsu A täitmine muuta süsteemi olekut selliselt, et tingimus C muutub vääraks, seega käivitatakse nii käsk A kui ka käsk B. Esimese variandi puhul täidetakse kindlasti ainult üks kahest käsust (A või B). Sellist erinevust näeme ka vastusevariantide C ja D võrdlemisel.

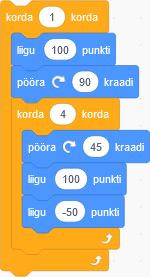
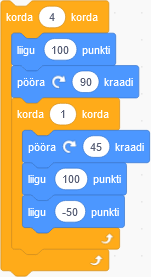
Põrandal liikuva roboti küljes on pliiats, mis jätab joone alati, kui ta liigub. Robot alustab valge põranda keskelt ja järgib neid juhiseid:
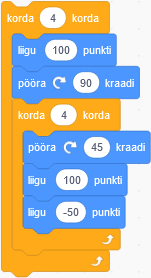
Paneme tähele, et:
Millise allolevatest joonistustest selline robot joonistab?
[Raadionupud]
A. 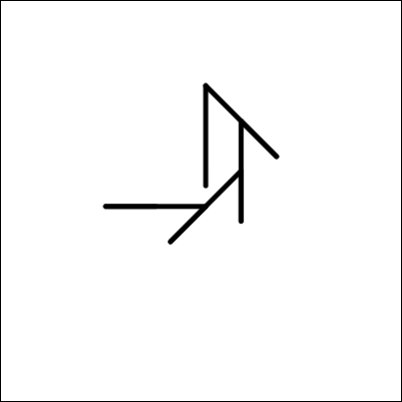
B. 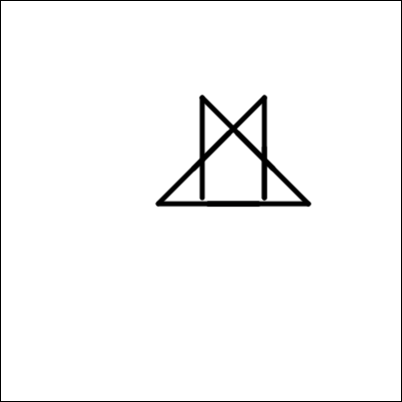
C. 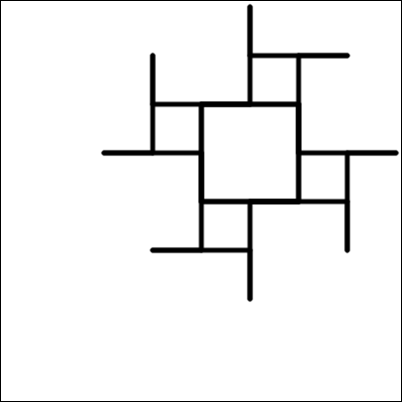
D. 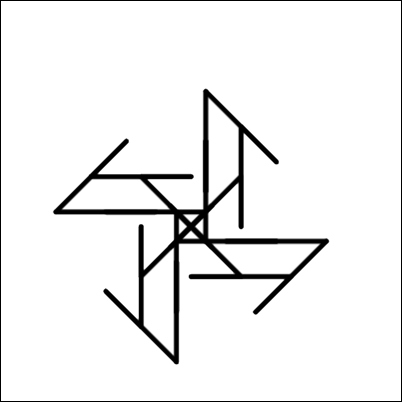
E. 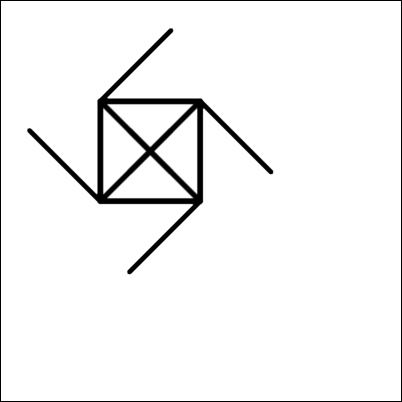
Õige vastus on: D.
Valede vastuste kõrvaldamiseks ja õige vastuse kindlaks tegemiseks on erinevaid viise. Üheks näiteks on joonte tõmbamise kordade loendamine (4 välimises ja igal korral omakorda 4 sisemises tsüklis, kokku seega 16), kuid tuleb olla ettevaatlik juhuks, kui joon tõmmatakse teise joone peale. See viitab kahele keerulisemale mustrile (pildid 3 ja 4 ülal). Seejärel võime vaadata 45-kraadiste pöörete arvu. See välistab pildi 3, jättes vastuseks pildi 4.
Teine viis selle probleemi lahendamiseks on proovida kõiki joonistusi algoritme järgides järele teha:
| Programm | Tulemus |
|---|---|
 |
 |
 |
 |
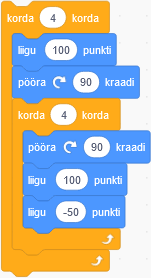 |
 |
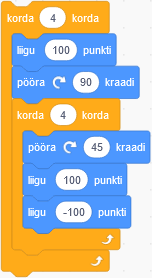 |
 |
Paljud looduses leiduvad mustrid sünnivad väga lihtsaid reegleid mitu korda korrates. Põrandaroboti või nn kilpkonnagraafikaga saab seda protsessi kasutada meid ennast huvitavate mustrite loomiseks. Selles ülesandes on selgelt näha programmeerimise ja antud juhul koodiplokkide kordamise jõud. Isegi mõned valed vastused on huvitavad ja on loodavad väikeste muudetuste abil.
Selle ülesande lahendamine eeldab kas programmi osadeks jagamist ja esitatud mustrite analüüsimist, et välistada need, mis antud programmiga ei kattu, või teise võimalusena programmi jälgimist sammhaaval, justkui me ise oleksime põrandarobotid. Need on mõlemad sobivad silumistehnikad, mida programmeerijad oma programmidest vigade otsimisel sageli kasutavad.

Järgnevas tekstilõigus on tühikud tähistatud märgiga '·' ja lõiguvahetused märgiga '¶'. Tähistamata reavahetused on tekstitöötlusprogrammi poolt automaatselt lisatud.
Loogika·on·teadus·mõtlemise·reeglitest·,struktuuridest·ja·vormidest.¶
Sõna·"loogika"·pärineb·algselt·vanakreeka·omadussõnast·λογική·(·logikē),·mis·on·
sõna·λογικός·(logikos;·'kõnega·seonduv·;·mõtlemisega·seonduv')·naissoovorm.Seda·
sõna·kasutati·kas·eraldi·nimisõnana·või·fraasis·λογικὴ·τέχνη(logikē·technē)·
'mõtlemiskunsti'·tähenduses.¶Mitmes sõnavahes on selle teksti vormistamisel tühikuid valesti kasutatud?
(Kui ühes sõnavahes on mitu viga, lugeda seda ainult üks kord.)
[Täisarv]
Õige vastus on: 5.
Esimene viga on 'reeglitest·,struktuuridest', kus tühik peaks olema koma järel, mitte selle ees.
Teine viga on 'λογική·(·logikē)', kus sulu järel ei peaks tühikut olema.
Kolmas viga on 'kõnega·seonduv·;·mõtlemisega·seonduv', kus semikooloni ees ei peaks tühikut olema.
Neljas viga on 'naissoovorm.Seda', kus punkti järel peaks tühik olema.
Viies viga on 'τέχνη(logikē', kus sulu ees peaks tühik olema.
Lisaks sellele, et kirjavahemärkide valesti kasutamine on eksimine õigekirjareeglite vastu, võib see tekstide arvutis töötlemisel kaasa tuua ka ebameeldivusi automaatse reapoolitusega. Kui jätta koma või punkti järele tühik panemata, ei saa tekstitöötlusprogramm sellesse kohta vajadusel reavahetust lisada; sellega võib kannatada teksti joondamine. Kui panna tühik koma või punkti ette, võib tekstitöötlusprogramm sinna automaatse reavahetuse lisada ja nii satub kirjavahemärk üksikuna järgmise rea algusse; ka see näeb inetu välja.
Samadel põhjustel käivad tühikud algava sulu ja algavate jutumärkide ette ning lõpetava sulu ja lõpetavate jutumärkide järele, aga ei käi algava sulu ja algavate jutumärkide järele ning lõpetava sulu ja lõpetavate jutumärkide ette.
Õigekirja seisukohalt võib arutada, kas 'reeglitest·,struktuuridest' on üks viga (tühik ja koma on omavahel vales järjekorras) või kaks viga (koma ees liigne tühik, koma järel vajalik tühik puudu). Selleks, et oleks üheselt selge, ongi ülesandes küsitud vigade arvu asemel nende sõnavahede arvu, kus on midagi valesti. Samasugust täpsust on vaja paljudes olukordades, kus erinevad osapooled (olgu inimesed või arvutid) peavad mingit reeglit kõik ühtemoodi mõistma — näiteks siis, kui eesti keele eksami etteütluse osas on hindamine määratud vigade arvuga.

Vaatame järgmist tabelarvutuse töölehte, mille mõnes lahtris on arvud ja mõnes valemid:

Töölehe funktsioon SUM arvutab antud piirkonna lahtrites olevate väärtuste summa, funktsioon MAX aga leiab antud piirkonna lahtrites olevatest väärtustest maksimaalse. Lahtrite piirkonnad on antud oma vasakpoolseima ülemise ja parempoolseima alumise lahtriga.
Milline väärtus tuleb tabeli lahtrisse C3?
[Täisarv]
Õige vastus on: 21.
Lihtne viis vastuse leidmiseks on kõigi lahtrite väärtused välja arvutada. Nii saame
B2 = SUM(A1:A3) = A1+A2+A3 = 1+6+7 = 14
B3 = SUM(A2:A4) = A2+A3+A4 = 6+7+8 = 21
B4 = SUM(A3:A5) = A3+A4+A5 = 7+8+4 = 19
C3 = MAX(A1:A3) = MAX(14;21;19) = 21Teine võimalus oleks panna tähele, et B3 väärtus erineb B2 väärtusest selle poolest, et summast jääb välja 1, aga lisandub 8; seega peab B3 väärtus olema suurem. Analoogiliselt saame, et B3 väärtus on suurem ka B4 omast. Seega on just B3 väärtus see maksimum, mille lahtris C3 olev valem valib ja võime piirduda ainult selle ühe summa väljaarvutamisega.
Tabelarvutuse töölehtede valemid võimaldavad korduvaid arvutusi automatiseerida ning sellega kasutajate aega kokku hoida ja käsitsi arvutamisest tulenevate vigade arvu vähendada.
Ka tabelarvutussüsteemid püüavad tehtava töö mahtu optimeerida. Kui me mingi lahtri väärtust muudame, siis arvutab süsteem üle ainult nende valemite väärtused, mis sellest lahtrist sõltuvad (ja siis need valemid, mis muutunud väärtustest sõltuvad jne). Meetod on küll erinev sellest, mida me eespool summade väljaarvutamise vältimiseks kasutasime, aga eesmärk on sama: teha vähem tühja tööd. Arvutid arvutavad küll kiiresti, aga väga suurte paljude valemitega töölehtede puhul on kokkuhoid ikka vajalik.

Kobraste Detektiivibüroo peab viie kurjategija kontodele ligi pääsemiseks ära arvama nende paroolid. Nad teavad juba järgmist:
Ana99stassia, A40nastassia või Anastassi17a.% & * # ! @ + $), näiteks Kopralinn@, Kobrasburg* või Puumetropol!.BRZT, AAAA või EZEZ.amiDen, neimaD või Dnmiea.ElLeNa, ELLena või Ellena.Detektiivid püüavad paroole ära arvata, proovides iga kurjategija puhul ükshaaval kõiki võimalikke tema mustrile vastavaid paroole. Selleks on neil olemas ka nimekiri kõigist 312 Kobrastoonia külast.
Kelle parooli nad tõenäoliselt kõige väiksema arvu katsetega ära arvavad?
[Raadionupud]
A. Anastassia
B. Bruno
C. Clara
D. Damieni
E. Ellena
Õige vastus on: E.
Tõenäoliselt arvavad detektiivid kõige kiiremini ära parooli, mille jaoks on kõige vähem võimalusi. Seetõttu arvutame, kui palju võimalusi on iga variandi puhul.
D, a, m, i, e või n), teise sümboli jaoks jääb järele 5 varianti (kuna kuuest võimalikust tähest valiti üks välja esimesele kohale), kolmanda jaoks 4 jne. Kokku seega 6·5·4·3·2·1=720 varianti.e või E, teise jaoks l või L jne. Kokku on võimalusi ainult 2·2·2·2·2·2=64.Seega on kõige väiksem variantide arv Ellenal.
Me arvutasime võimaluste arvu täpselt välja kõigi paroolide puhul, kuid piisaks ka sellest, kui teeksime seda ainult Ellena jaoks ja võrdleksime seda tulemust väga üldiselt teiste variantidega (näiteks 90 kahekohalist arvu, 312 küla jne).
Sellel ülesandel on vähemalt kaks seost informaatika ja arvutusliku mõtlemisega.
Esiteks kasutavad paljud inimesed mingit mustrit, kui nad peavad uue parooli välja mõtlema. Nagu sellest ülesandest näha: mida lihtsam on muster, seda lihtsam on kellelgi teisel kõiki võimalusi proovides parooli ära arvata. Ärge unustage, et arvutitega saab paroole proovida automaatselt, seega palju kiiremini kui inimesed, ilma et neil igav hakkaks.
Hea parool koosneb paljudest väiketähtedest, suurtähtedest, numbritest, erimärkidest, näiteks 2kb-C6xV!/<)^-U. Kui arvestame näiteks 26 väike- ja 26 suurtähe, 10 numbri ja 10 erimärgiga, siis on 15-märgilisi paroole kokku 7215=7244150201408990671659859968! On olemas rakendusi, mis genereerivad selliseid paroole ja aitavad neid kasutajal ka meeles pidada (või täpsemalt peavad neid kasutaja eest meeles).
Teine hea võimalus, kui kasutatav süsteem seda lubab, on võtta parooliks ühe lühikese sõna asemel mitmest sõnast koosnev fraas, näiteks correct horse battery staple. Kasutades 50000 sõnaga sõnaraamatut, saab selliseid neljasõnalisi fraase moodustada 500004=6250000000000000000. Seda on küll vähem kui eelmises näites, aga siiski päris palju. Samas on selliseid fraase oluliselt lihtsam meeles pidada ja seega sobivad nad ka siis, kui paroolitasku rakendust millegipärast kasutada ei saa.
Teiseks peab programmeerija oskama hinnata, kui kaua mingi arvutus tõenäoliselt aega võtab. Arvutiteadlased nimetavad seda "algoritmide arvutusliku keerukuse määramiseks". Kasutasime sõna "tõenäoline", sest teoreetiliselt on võimalik, et esimene parool, mida proovime, on õige, isegi neil juhtudel, kui võimalusi on miljardeid. Aga võib ka juhtuda, et meil ei vea üldse ja leiame õige parooli alles viimase võimaliku variandina. Keskmiselt leiame õige parooli poolel teel kõigi võimaluste kontrollimisel.

Programmeerimises kasutatakse for-kordust mingite tegevuste etteantud arv kordi kordamiseks.
Allolevas näites pannakse i väärtuseks järjest arvud 1, 2 ja 3 ning iga kord täidetakse korduse kehas (taandega osas) olev käsk; paneme tähele, et selles käsus saab i väärtust kasutada:
for i from 1 to 3
print(i)väljastab tulemuse
1
2
3Operaator * (tärn) tähistab arvude puhul korrutamist, teksti puhul selle kordamist:
for i from 1 to 3
print(i * "x")väljastab tulemuse
x
xx
xxxMillise mustri saame, kui kasutame allolevat koodilõiku?
for i from 1 to 5
print(((6 - i) * 2) * "x")
for i from 1 to 5
print((i * 2) * "x")[Raadionupud]
A.
xxxxxxxxxx
xxxxxxxx
xxxxxx
xxxx
xx
xx
xxxx
xxxxxx
xxxxxxxx
xxxxxxxxxxB.
xxxxxxxxxx
xxxxxxxx
xxxxxx
xxxx
xx
xx
xxxx
xxxxxx
xxxxxxxx
xxxxxxxxxxC.
xx
xxxx
xxxxxx
xxxxxxxx
xxxxxxxxxx
xxxxxxxxxx
xxxxxxxx
xxxxxx
xxxx
xxD.
xx
x x
x x
x x
x x
x x
x x
x x
x x
xxÕige vastus on: A.
Kõik teised variandid saame kiiresti välistada, pannes tähele, et programm ei trüki tühikuid (" ") ning vastusevariant A on ainus, mis neid ei sisalda.
Siin tutvustatud for-kordus esineb peaaegu kõigis programmeerimiskeeltes. Korduseid kasutatakse, nagu nimigi ütleb, programmiosade korduvaks täitmiseks; for-kordus sobib siis, kui korduste arv on ette teada.
Operaatorite kasutamist erinevatel eesmärkidel olenevalt andmete tüübist nimetatakse operaatorite ülelaadimiseks või polümorfismiks. Polümorfismi kasutatakse programmeerimiskeeltes enamasti selle tõttu, et operaatorite arv on piiratud ja võimalike operatsioonide arv ületab tunduvalt saadaolevate operaatorite arvu.
Hea tava on operaatorite ülelaadimisel anda neile "tavalisega" võimalikult sarnane tähenduse. Nii on loogiline, et * tähistab arvude puhul korrutamist ja teksti puhul selle kordamist, samas kui + tähistab arvude puhul liitmist ja tekstide puhul nende kokkukleepimist:
print("a" + "b")väljastab
ab
Ahelkood on kokkuhoidlik viis must-valgel pildil olevate kontuuride (piirjoonte) esitamiseks. Põhimõte on valida üks must piksel ja salvestada igal sammul suund liikumiseks järgmise musta pikslini kontuuri päripäeva (kellaosuti liikumise suunas) läbimisel.
Suunad on tähistatud numbritega selliselt:
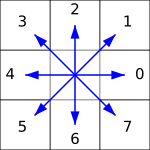
Näiteks kui valime alloleval pildil esimeseks sinise raamiga tähistatud piksli, saame edasi liikuda punaste nooltega näidatud suundades ja tulemuseks on ahelkood 1, 0, 0, 7, 7, 5, 5, 4, 3, 3, 2.
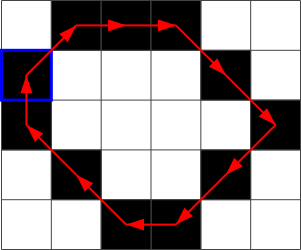
Vaatame nüüd sellist pilti:

Milline järgmistest ei ole selle pildi ahelkood?
[Raadionupud]
A. 1, 1, 1, 0, 7, 7, 7, 6, 5, 5, 5, 4, 3, 3, 3, 2
B. 7, 6, 5, 5, 5, 5, 4, 3, 3, 2, 1, 1, 1, 1, 0, 7
C. 5, 5, 5, 4, 3, 3, 3, 2, 1, 1, 1, 0, 7, 7, 7, 6
D. 3, 3, 2, 1, 1, 1, 0, 7, 7, 7, 6, 5, 5, 5, 4, 3
Õige vastus on: B.
Järgnevad joonised illustreerivad vastusevariantides olevate ahelkoodide saamist:
A. 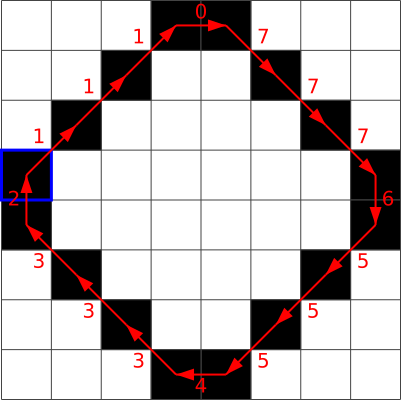 B.
B. 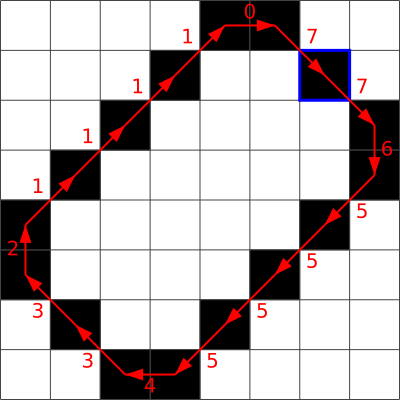
C. 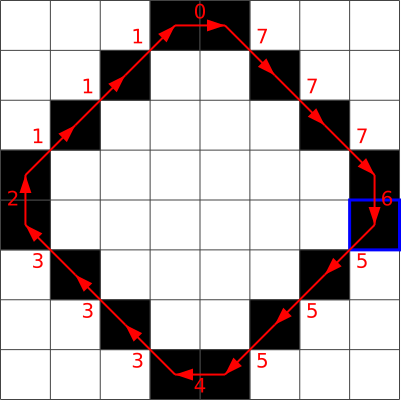 D.
D. 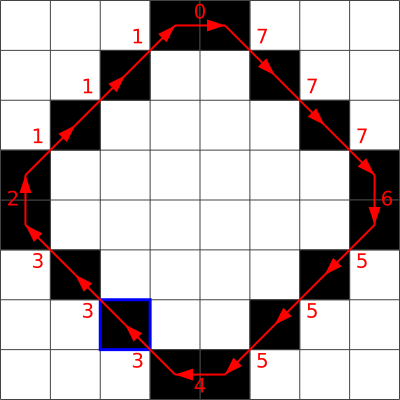
Ahelkood on üks meetod objektide esitamiseks nende kontuuride abil. Ahelkood on määratud stardipiksli määramisega ja suunavektorite jadaga vastavalt sellele, kas igal sammul suundutakse kontuuri järgmise musta pikslini vasakul, paremal, üleval, all või diagonaalis. Ahelkoodi eeliseks on vajaliku info säilitamine ja samas andmemahu väga suur kokkuhoid. Esimesena esitles ahelkoodi ideed Freeman 1961. aastal ning seepärast on see tuntud ka kui Freemani ahelkood (ingl Freeman Chain Code, FCC).
Ahelkoodi üks kasutusala on numbrituvastus. Esiteks võimaldab see kood objekte kompaktselt esitada, teiseks on ahelkoodide võrdlemine lihtsam kui piltide võrdlemine. Lisaks sellele on ahelkoodist võimalik välja lugeda ka kujutatava objekti üksikuid omadusi. Ahelkoodid esindavad kadudeta tihendamist ja säilitavad kogu info, mis on vajalik kiireks ja efektiivseks mustrite analüüsiks.
Copyright © 2022 Bebras – International Challenge on Informatics and Computational Thinking.
Licensed under Creative Commons Attribution-ShareAlike 4.0 International License.
Flag icons by GoSquared.