











В замке под названием Мистика живёт волшебник. Волшебник может сам превращаться либо в фею, либо создавать фею с правой стороны от себя. Фея может превращаться в зелье (слева) и дракона (справа) или зелье (слева), волшебника (в центре) и дракона (справа).
Следующая таблица показывает результаты возможных превращений:
| До | После |
|---|---|
 |
 |
 |
  |
 |
  |
 |
   |
Эти волшебные превращения могут происходить сколько угодно раз и в любом порядке: любой волшебник и любая фея могут изменяться в любое время.
Если начать с одного волшебника, то какой порядок невозможен в Мистике?
[Raadionupud]
A. 




B. 







C. 





D. 



На берегу реки лежат брёвна разных размеров. Задача Генриха состоит в том, чтобы расположить брёвна по порядку так, чтобы самые маленькие были с левого конца ряда, а самые большие — с правого конца. Генрих идёт вдоль берега реки, при этом он всегда останавливается между двумя брёвнами. Он сравнивает размеры двух брёвен и при необходимости меняет их местами.
Генрих знает, что, независимо от первоначального порядка брёвен, он всегда может их правильно отсортировать следующим способом:
Давайте посмотрим, как, используя такой способ, Генрих сортирует брёвна:
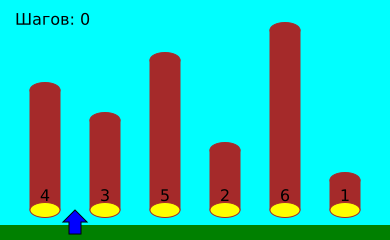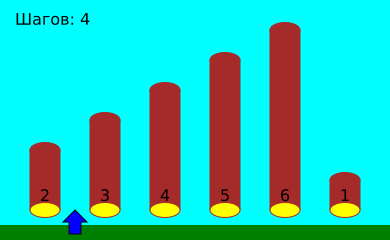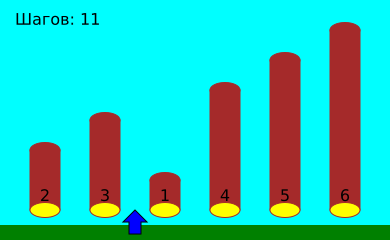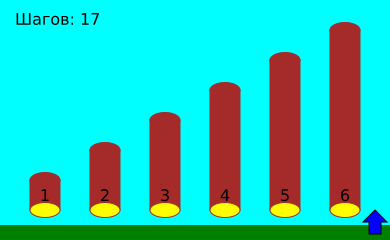
В этом примере Генрих должен сделать всего 17 шагов влево и вправо.
Количество шагов, которые Генрих должен выполнить при сортировке, зависит от первоначального порядка брёвен. В случае шести брёвен и в самом худшем случае он должен сделать 25 шагов.
Сколько шагов должен сделать Генрих при сортировке 60 брёвен?
[Raadionupud]
A. [0...30]
B. [6...70]
C. [59...300]
D. [59...3600]
Ученики одного класса общаются друг с другом как показано на рисунке. Например, в течение дня ученик H общается только с D, E и F.
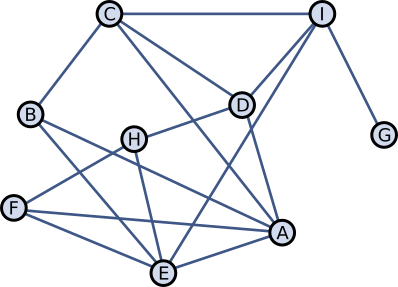
В понедельник на работу пришла новая учительница математики, которую два ученика за её причёску тут же прозвали "мисс Бесконечность". Прозвище распространялось среди учеников таким образом, что каждый ученик, у которого больше половины собеседников уже стало использовать это прозвище, сам на следующий школьный день стал так называть учительницу.
В скором времени новое прозвище стали использовать все ученики класса.
Кто были эти два ученика, которые придумали прозвище?
(Запиши только буквы (без всяких других символов), под которыми "спрятались" эти два ученика. Например, AB. Если существует несколько решений, то запиши любое из них.)
[Tekstikast]
В пекарне дядюшки Бобра продаются пирожные в коробках, чтобы их было удобно дарить друзьям. Используются коробки двух видов: 4-х местные, куда аккуратно помещается именно четыре пирожных, и 7-ми местные для семи пирожных.
На один противень вмещается до 100 пирожных. Иногда на нём выпекают такое количество пирожных, которое нельзя разместить в 4-х или 7-ми местные коробки без того, чтобы какое-нибудь пирожное да и не поместилось. Например, в такие коробки нельзя точно поместить 3 или 5 пирожных; есть и другие наборы (с разным количеством пирожных), которые не подойдут.
Какое будет наибольшее количество пирожных, которое можно испечь на этом противне, но нельзя упаковать в эти коробки так, чтобы какое-нибудь пирожное не поместилось?
[Täisarv]
Дрон взлетает с некоторой белой клетки, которая находится на квадратном поле, в направлении параллельном краю таблицы.

Далее дрон посещает точно восемь белых клеток, следуя следующим правилам:
Сколько всего возможных стартовых клеток есть на поле?
[Täisarv]
Шесть друзей выбирают, какой из семи фильмов посмотреть. Друзья оценивают фильмы так:
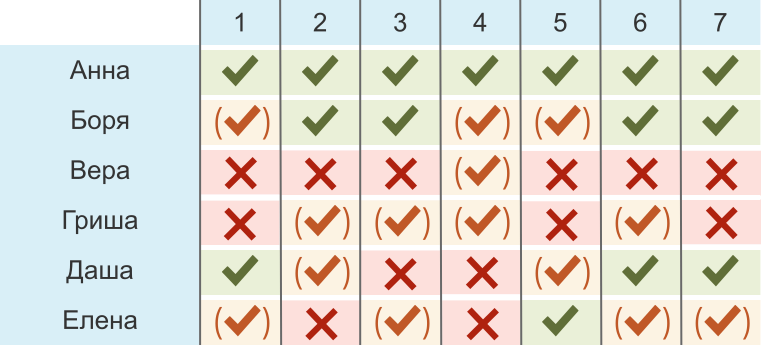
Оценки от лучшего к худшему выглядят следующим образом: 


Фильм становится любимым, если все друзья ставят ему наивысшую оценку среди всех свои оценок. Например, фильм №1 не является любимым фильмом, потому что Вера дала свою лучшую оценку фильму №4.
Каково наименьшее возможное количество изменений оценок, чтобы фильм стал любимым?
[Täisarv]
Белла попросила у своей подруги Анны номер телефона. Так как Анна не хочет, чтобы другие знали её номер телефона, то она передала бумажку, где номер телефона был засекречен. Позже Анна объяснила Белле, что номер был закодирован следующим образом:
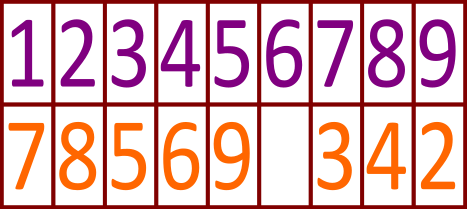
Что из нижеприведённого является номером телефона Анны?
[Raadionupud]
A. 123 456 789
B. 785 691 342
C. 173 592 846
D. 173 859 246
Саша и Питер — соседи: окна их комнат напротив друг друга через улицу. Каждый день они играют в игру: вечером перед сном оба записывают число на бумажке и приклеивают её на своё окно. Утром оба смотрят на число на противоположном окне, прибавляют его к своему числу и прикрепляют к своему окну новую бумажку с полученной суммой. Выигрывает тот, у кого на окне на бумажке оказывается наименьшее число.
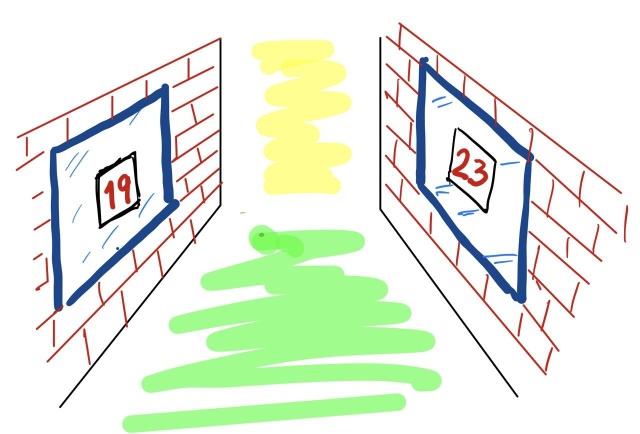
У детей каникулы и они просыпаются в разное время, поэтому окончательные числа на окнах зависят от того, когда каждый из них проснётся. Допустим, что перед сном Саша записал число 19, а Питер — 23. Если бы Саша проснулся раньше Питера, то он бы заменил число 19 на своём окне на число 42. Тогда Питер увидел бы число 42 и приклеил бы на своё окно бумажку с числом 65; следовательно, Саша выиграл бы. Если бы оба проснулись одновременно, то они оба записали бы 42, и игра закончилась бы ничьей.
Предположим, что перед сном Саша записывает число 25, а Питер — число 47.
Какой из следующих вариантов невозможен?
[Raadionupud]
A. Саша запишет 72, и Питер запишет 119; значит, Саша выиграет.
B. Саша запишет 97, и Питер запишет 119; значит, Саша выиграет.
C. Саша запишет 72, и Питер запишет 72; значит, игра закончится ничьей.
D. Саша запишет 97, и Питер запишет 72; значит, Питер выиграет.
На экране компьютера мы видим рисунок лягушки. Однако цвет лягушки неизвестен.

Для изменения цвета у нас имеется четыре программы, но мы можем запустить только одну из них. Мы хотим быть уверенными, что по завершению работы программы мы получим лягушку именно зелёного цвета, вне зависимости от её первоначального цвета.
Какая программ не гарантирует, что в конце её работы лягушка будет зелёного цвета?
[Raadionupud]
A.
Если лягушка красная, то покрась её в жёлтый, в противном случае — в зелёный.
Если лягушка жёлтая, то покрась её в красный.
Если лягушка не жёлтая, то покрась её в зелёный.B.
Если лягушка красная, то покрась её в жёлтый.
Если лягушка не красная, то покрась её в зелёный.
Если лягушка жёлтая, то покрась её в красный, в противном случае — в зелёный.C.
Если лягушка жёлтая, то покрась её в зелёный.
Если лягушка не жёлтая, то покрась её в красный.
Если лягушка красная, то покрась её в зелёный, в противном случае — в жёлтый.D.
Если лягушка жёлтая, то покрась её в зелёный, в противном случае — в красный.
Если лягушка красная, то покрась её в зелёный, в противном случае — в жёлтый.У перемещающегося по полу робота сбоку имеется карандаш. Каждый раз, когда робот двигается, карандаш оставляет линию. Робот стартует с центра белого пола и следует следующим командам:
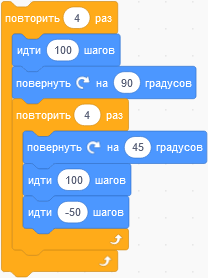
Обратите внимание, что:
Какое из нижеприведённых изображений нарисует такой робот?
[Raadionupud]
A. 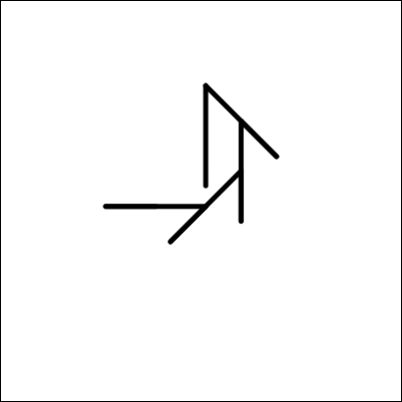
B. 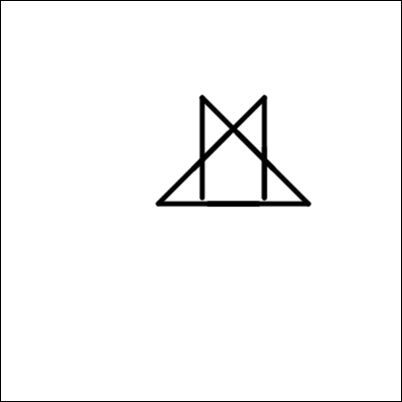
C. 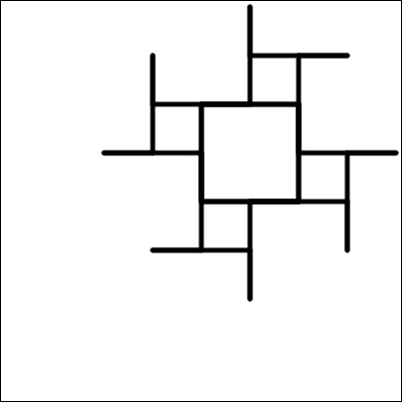
D. 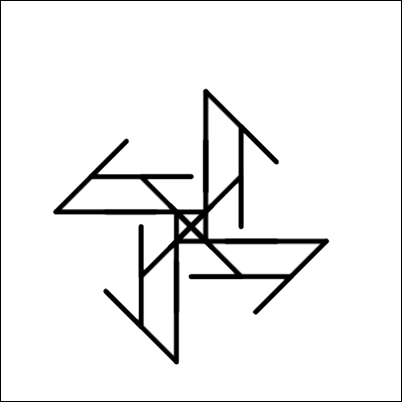
E. 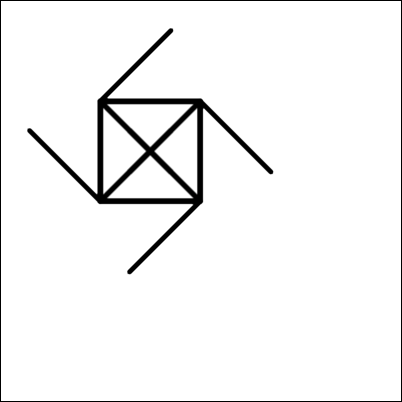
В приведённом тексте пробелы отмечены символом '·', а переходы на новые абзацы символом '¶'. Неотмеченные переходы на новую строку автоматически добавляются текстовым процессором.
Логика·—·это·наука·о·правилах·,структурах·и·формах·мышления.
Слово·«логика»·первоначально·происходит·от·древнегреческого·прилагательного·
λογική·(·logikē),·которое·является·женской·формой·λογικός·(logikos;·«относящийся·
к·речи·;·относящийся·к·мышлению»).·Слово·использовалось·либо·как·отдельное·
существительное,либо·во·фразе·λογικὴ·τέχνη(logikē·technē)·в·смысле·«искусство·
мышления».Сколько существует пар слов, между которыми при оформлении текста пробелы были использованы неправильно?
(Если в одной паре допущено несколько ошибок, то считай это за одну ошибку.)
[Täisarv]
Рассмотрим следующий лист электронной таблицы, где в некоторых ячейках содержатся числа, а в некоторых — формулы:

Имеющаяся на рабочем листе функция SUM вычисляет сумму значений в ячейках заданного диапазона, а функция MAX находит наибольшее (максимальное) значение в ячейках заданного диапазона. Диапазоны ячеек задаются их крайними левыми верхними и крайними правыми нижними ячейками.
Какое значение появится в табличной ячейке C3?
[Täisarv]
Детективное бюро Бобрики должно выяснить пароли пяти преступников, чтобы получить доступ к их учётным записям. Они уже знают следующее:
Ana99stassia, A40nastassia или Anastassi17a.% & * # ! @ + $), например, Боброград@, Бобробург* или Древорополь!.BRZT, AAAA или EZEZ.amiDen, neimaD или Dnmiea.ElLeNa, ELLena или Ellena.Детективы пытаются выяснить пароли, перебирая один за другим все возможные варианты, соответствующие паттерну каждого преступника. Для этого у них также есть список всех 312 деревень в Кобрастонии.
Чей пароль они, скорее всего, выяснят за наименьшее количество попыток?
[Raadionupud]
A. Анастассии
B. Бруно
C. Веры
D. Дамиэна
E. Эллены
В программировании for-повторение используется для повторения некоторых действий заданное количество раз.
В нижеприведённом примере значения i устанавливаются подряд и ими служат числа 1, 2 и 3, и каждый раз выполняется расположенная в теле команда повторения (часть с отступом); обратите внимание, что в этой команде можно использовать значение i:
for i from 1 to 3
print(i)получим результат
1
2
3Для чисел оператор * (звёздочка) означает умножение, а для текста — его повторение:
for i from 1 to 3
print(i * "x")получим результат
x
xx
xxxКакой паттерн мы получим, если воспользуемся нижеприведённым фрагментом кода?
for i from 1 to 5
print(((6 - i) * 2) * "x")
for i from 1 to 5
print((i * 2) * "x")[Raadionupud]
A.
xxxxxxxxxx
xxxxxxxx
xxxxxx
xxxx
xx
xx
xxxx
xxxxxx
xxxxxxxx
xxxxxxxxxxB.
xxxxxxxxxx
xxxxxxxx
xxxxxx
xxxx
xx
xx
xxxx
xxxxxx
xxxxxxxx
xxxxxxxxxxC.
xx
xxxx
xxxxxx
xxxxxxxx
xxxxxxxxxx
xxxxxxxxxx
xxxxxxxx
xxxxxx
xxxx
xxD.
xx
x x
x x
x x
x x
x x
x x
x x
x x
xxЦепной код — это экономный способ представления контуров (границ) на чёрно-белых изображениях. Суть заключается в выборе одного чёрного пикселя и сохранении на каждом этапе прохождения контура по движению часовой стрелки направления, которое позволит добраться до следующего чёрного пикселя.
Направления отмечены цифрами следующим образом:
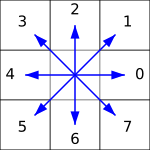
Например, если на нижеприведённом изображении стартовый пиксель отмечен синей рамкой, то дальше можно двигаться в отмеченных красными стрелками направлениях. Как результат, цепной код будет 1, 0, 0, 7, 7, 5, 5, 4, 3, 3, 2.
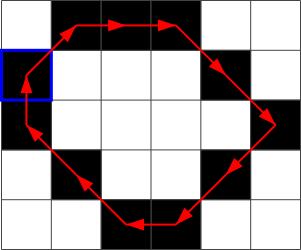
Рассмотрим теперь такое изображение:

Что из приведённого не будет цепным кодом этого изображения?
[Raadionupud]
A. 1, 1, 1, 0, 7, 7, 7, 6, 5, 5, 5, 4, 3, 3, 3, 2
B. 7, 6, 5, 5, 5, 5, 4, 3, 3, 2, 1, 1, 1, 1, 0, 7
C. 5, 5, 5, 4, 3, 3, 3, 2, 1, 1, 1, 0, 7, 7, 7, 6
D. 3, 3, 2, 1, 1, 1, 0, 7, 7, 7, 6, 5, 5, 5, 4, 3