

В замке под названием Мистика живёт волшебник. Волшебник может сам превращаться либо в фею, либо создавать фею с правой стороны от себя. Фея может превращаться в зелье (слева) и дракона (справа) или зелье (слева), волшебника (в центре) и дракона (справа).
Следующая таблица показывает результаты возможных превращений:
| До | После |
|---|---|
 |
 |
 |
  |
 |
  |
 |
   |
Эти волшебные превращения могут происходить сколько угодно раз и в любом порядке: любой волшебник и любая фея могут изменяться в любое время.
Если начать с одного волшебника, то какой порядок невозможен в Мистике?
[Raadionupud]
A. 




B. 







C. 





D. 



Правильный ответ: B.
Пронумеруем волшебные превращения следующим образом:
| Номер | До | После |
|---|---|---|
| 1 |  |
 |
| 2 |  |
  |
| 3 |  |
  |
| 4 |  |
   |
Вариант A возможен, если мы начнём с одного волшебника и применим превращения 1, 4, 2 и 3.
Вариант C возможен, если мы начнём с одного волшебника и применим превращения 2, 2, 3, 4 и 1.
Вариант D возможен, если мы начнём с одного волшебника и применим превращения 2, 1, 3 и 3.
Один из быстрых способов определить, что вариант B невозможен, — это заметить, что правила превращения всегда создают и зелье, и дракона одновременно. Поэтому в Мистике количество зелья всегда должно быть равно количеству драконов, а в варианте B это не так.
Волшебные превращения можно рассматривать как набор правил, используемых для создания паттернов из объектов в Мистерии.
В информатике имеется инструмент контекстно-свободной грамматики, который можно использовать для описания правил, генерирующих паттерны. Контекстно-свободные грамматики могут описывать как формальные, так и естественные языки: многократно применяя правила грамматики, мы можем генерировать слова, который и образуют язык.
В этом задании нам по сути пришлось определять, какое из заданных слов не принадлежит к «языку Мистики».

На берегу реки лежат брёвна разных размеров. Задача Генриха состоит в том, чтобы расположить брёвна по порядку так, чтобы самые маленькие были с левого конца ряда, а самые большие — с правого конца. Генрих идёт вдоль берега реки, при этом он всегда останавливается между двумя брёвнами. Он сравнивает размеры двух брёвен и при необходимости меняет их местами.
Генрих знает, что, независимо от первоначального порядка брёвен, он всегда может их правильно отсортировать следующим способом:
Давайте посмотрим, как, используя такой способ, Генрих сортирует брёвна:
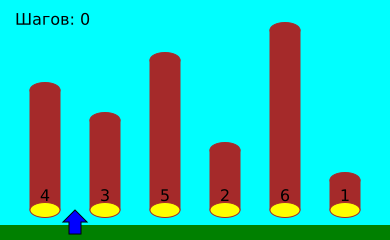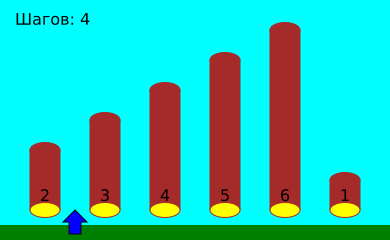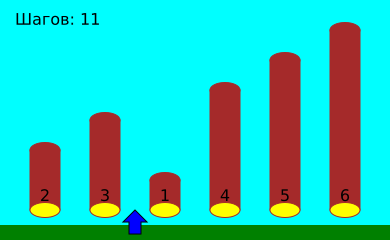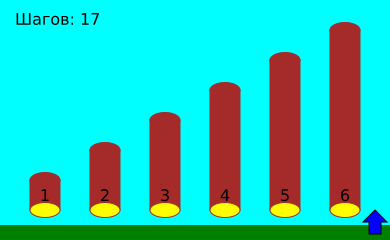
В этом примере Генрих должен сделать всего 17 шагов влево и вправо.
Количество шагов, которые Генрих должен выполнить при сортировке, зависит от первоначального порядка брёвен. В случае шести брёвен и в самом худшем случае он должен сделать 25 шагов.
Сколько шагов должен сделать Генрих при сортировке 60 брёвен?
[Raadionupud]
A. [0...30]
B. [6...70]
C. [59...300]
D. [59...3600]
Правильный ответ: D.
[0...30] неправильный ответ. Даже в самом лучшем случае, когда все брёвна первоначально уже расположены в правильном порядке, Генрих должен сделать 59 шагов (а это больше 30), чтобы добраться до конца ряда.
[6...70] и [59..300] также неправильные ответы. Чтобы доказать это, нам нужно изучить наихудший случай, когда брёвна изначально расположены в обратном порядке. В этом случае Генрих доходит до бревна, расположенного на k-й позиции и перетаскивает его в первую, то есть крайнюю левую позицию. Далее он идёт к бревну, которое находится на k+1 позиции. Таким образом, для того чтобы добраться до бревна на k-й позиции, Генрих делает k–2 шагов, и k–2 шагов, чтобы перетащить бревно в начало ряда. Значит, на все брёвна ему потребуется в общей сложности сделать 2·(0+1+2+...+58) шагов. В конце ему потребуется еще 59 шагов, чтобы добраться до конца ряда. Сумма шагов будет в итоге равна 59^2=3481, и это число не принадлежит ни к одному из этих двух промежутков.
[59...3600] правильный ответ. Чтобы убедиться в этом, нам нужно доказать, что предполагаемый наихудший случай на самом деле является наихудшим. Когда Генрих дойдёт до расположенного на k-й позиции бревна, то все брёвна слева от этого бревна уже будут находиться в правильном порядке, и ему нужно будет только перетащить новое бревно на правильное место среди предыдущих. Для этого, однако, ему потребуется сделать настолько больше шагов, насколько левее нужно перетащить это бревно. Затем он пойдёт к бревну на позиции k+1, где повторяется та же логика. Так что на самом деле наихудший случай — это когда каждое следующее бревно необходимо перетащить в левый конец очереди.
Сортировка или размещение в определённом порядке объектов, находящихся в последовательности, является классической задачей в информатике. Наиболее часто используемыми являются числовой порядок (для чисел) и алфавитный порядок (для текстов). Эффективное упорядочение важно для многих других алгоритмов (например, для алгоритма поиска), которые требуют упорядоченных вводных данных. Сортировка также может быть полезна для нормализации данных и создания удобочитаемых выходных данных.
Одним из известных алгоритмов сортировки является так называемая гномья сортировка (англ gnome sort). Этот алгоритм прост и за раз работает с одним элементом последовательности, перемещая элемент в правильное положение с помощью обмена элементов. Гномья сортировка (которую также называют глупой сортировкой) была предложена Хамидом Сарбази-Асадом, профессором компьютерных наук из Технологическом университета Шарифа, в 2000 году.
Говоря об алгоритме, вы всегда должны думать о том, насколько он быстр, то есть какое количество операций он требует в зависимости от количества элементов. Если у нас есть N брёвен, то в худшем случае потребуется примерно N2 операций для их сортировки при помощи гномьего метода. В информатике это называется квадратичной сложностью. Остальные ответы в этом задании представляют другие варианты сложностей: постоянная сложность для [0..30], линейная сложность для [6..70] и линейно-логарифмическая сложность для [59...300].

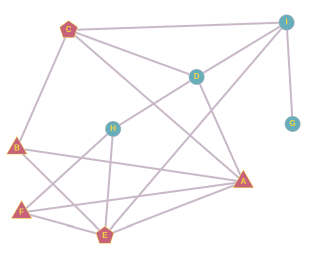
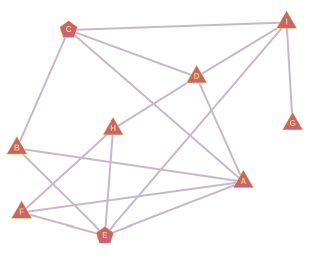
Ученики одного класса общаются друг с другом как показано на рисунке. Например, в течение дня ученик H общается только с D, E и F.
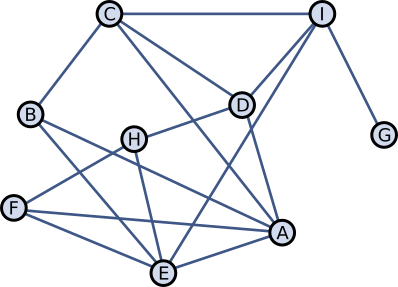
В понедельник на работу пришла новая учительница математики, которую два ученика за её причёску тут же прозвали "мисс Бесконечность". Прозвище распространялось среди учеников таким образом, что каждый ученик, у которого больше половины собеседников уже стало использовать это прозвище, сам на следующий школьный день стал так называть учительницу.
В скором времени новое прозвище стали использовать все ученики класса.
Кто были эти два ученика, которые придумали прозвище?
(Запиши только буквы (без всяких других символов), под которыми "спрятались" эти два ученика. Например, AB. Если существует несколько решений, то запиши любое из них.)
[Tekstikast]
Правильный ответ: CE или DE.
Во-первых, заметим, что для начала распространения прозвища у этих двух учеников должен быть общий собеседник. В свою очередь у общего собеседника должно быть в итоге ровно три собеседника. Если у общего собеседника больше собеседников, то два ученика, придумавших прозвище, не будут в большинстве. Если у общего собеседника есть два собеседника, то ими будут сами ученики, придумавшие прозвище, и тогда это прозвище дальше не распространится. У учеников B, F и H ровно по три собеседника.
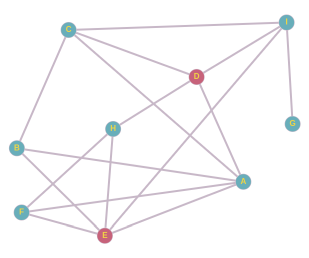
От ученика B мы можем образовать три пары: A и C, A и E, C и E. Если бы A и C придумали прозвище, то B использовал бы его уже на следующий день, но дальше оно не распространилось бы. Если бы прозвище придумали А и Е, то B и F использовали бы его уже на следующий день, а через день и H, но дальше оно не распространилось бы. Если бы прозвище придумали C и E, оно бы распространилось следующим образом:
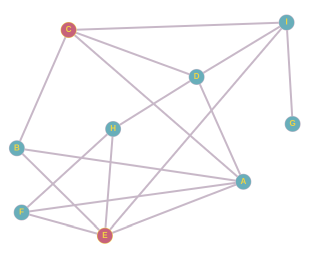
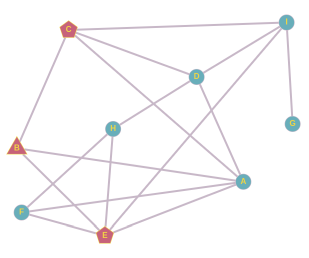
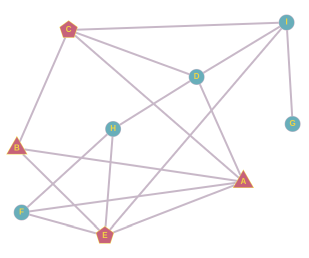
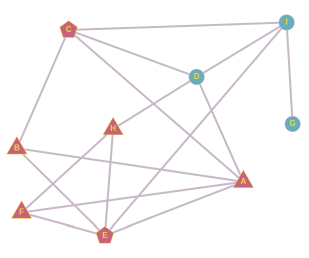
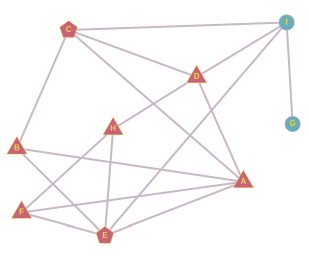
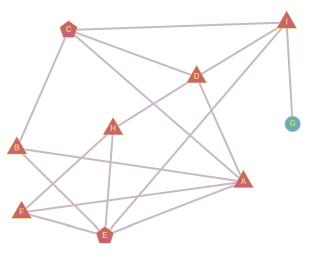
Как и в случае ученика B, от ученика F мы можем образовать пары A и E, A и H, E и H. Мы уже проанализировали пару A и E. Если бы прозвище придумали А и Н, то F использовал бы его уже на следующий день, затем E, и затем B, но дальше прозвище не распространилось бы. Если бы прозвище придумали E и H, то F использовал бы его уже на следующий день, и на этом всё.
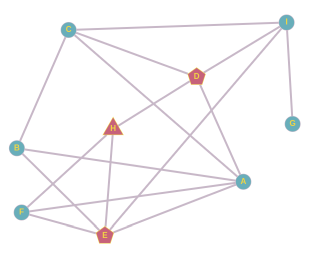
От собеседника H мы можем образовать пары D и E, D и F, E и F. Если бы прозвище придумали E и F или D и F, то его распространение закончилось бы опять на ученике H. Если бы прозвище придумали D и E, оно бы распространилось следующим образом:
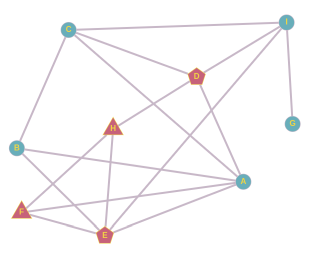
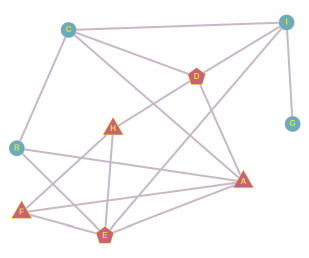
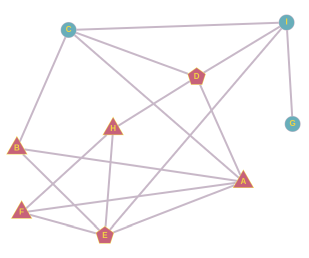
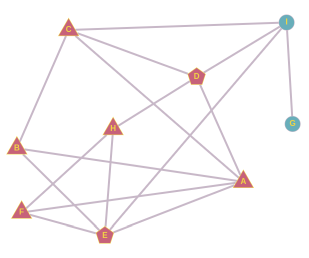
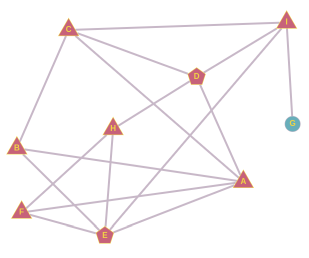
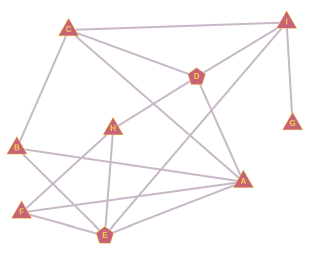
На этом мы исчерпали все возможности. Следовательно, правильный ответ: CE или DE.
Социальные сети играют большую роль в распространении информации, идей и точек зрения. Мысль, которая окажется в социальной сети, быстро распространится или исчезнет. Исследования скорости распространения информации в социальных сетях является очень популярным направлением информатики, а увеличение этой скорости стал важной отраслью в мире рекламы.
Это задание сосредоточилось на так называемой пороговой модели (англ threshold model), где у каждого человека есть порог, то есть количество контактов, который должен быть активным (в данном случае это означает использование нового прозвища), чтобы и человек сам стал активным (то есть и сам начал использовать это прозвище).

В пекарне дядюшки Бобра продаются пирожные в коробках, чтобы их было удобно дарить друзьям. Используются коробки двух видов: 4-х местные, куда аккуратно помещается именно четыре пирожных, и 7-ми местные для семи пирожных.
На один противень вмещается до 100 пирожных. Иногда на нём выпекают такое количество пирожных, которое нельзя разместить в 4-х или 7-ми местные коробки без того, чтобы какое-нибудь пирожное да и не поместилось. Например, в такие коробки нельзя точно поместить 3 или 5 пирожных; есть и другие наборы (с разным количеством пирожных), которые не подойдут.
Какое будет наибольшее количество пирожных, которое можно испечь на этом противне, но нельзя упаковать в эти коробки так, чтобы какое-нибудь пирожное не поместилось?
[Täisarv]
Правильный ответ: 17.
В данные коробки можно упаковать 4, 7, 8, 11, 12, 14, 15, 16, 18, 19, 20, 21 и т.д. пирожных. Если у нас есть четыре последовательных числа пирожных, которые можно упаковать (например, от 18 до 21), то мы можем упаковать и все бОльшие числа, добавив достаточное количество 4-х местных коробок к некоторым из предыдущих комбинаций (7-ми местными коробками мы можем уменьшить количество используемых коробок, но это уже не влияет на принципиальное решение "может/нельзя"). Таким образом, наибольшее число пирожных, которое нельзя упаковать в эти коробки, равно 17.
Проблема монеты (или проблема Фробениуса) — это математическое задание, в котором ищется наибольшая сумма (число Фробениуса), которая не может быть оплачена монетами данных номиналов. Если у нас имеется монета номиналом 1, то у нас нет проблем ни с одним из чисел, но если мы исключим эту монету, некоторые суммы не могут быть оплачены точно. Если у нас есть монеты только с двумя номиналами A и B, то число Фробениуса этого комплекта равно A·B–A–B.
Для любого количества номиналов нет такой простой формулы, но есть алгоритмы. Например, можно воспользоваться динамическим программированием: изначально мы предполагаем, что данными монетами можно оплатить только сумму 0. Затем для каждой последующей суммы X мы проверяем, существует ли такой номинал Y, чтобы сумма X–Y входила бы в число сумм, которые можно оплатить. Если найдётся такой Y, то мы можем добавить X к суммам, подлежащим оплате.

Дрон взлетает с некоторой белой клетки, которая находится на квадратном поле, в направлении параллельном краю таблицы.

Далее дрон посещает точно восемь белых клеток, следуя следующим правилам:
Сколько всего возможных стартовых клеток есть на поле?
[Täisarv]
Правильный ответ: 8.
Чтобы найти ответ, сначала обратим внимание на то, что есть четыре подходящих пути:
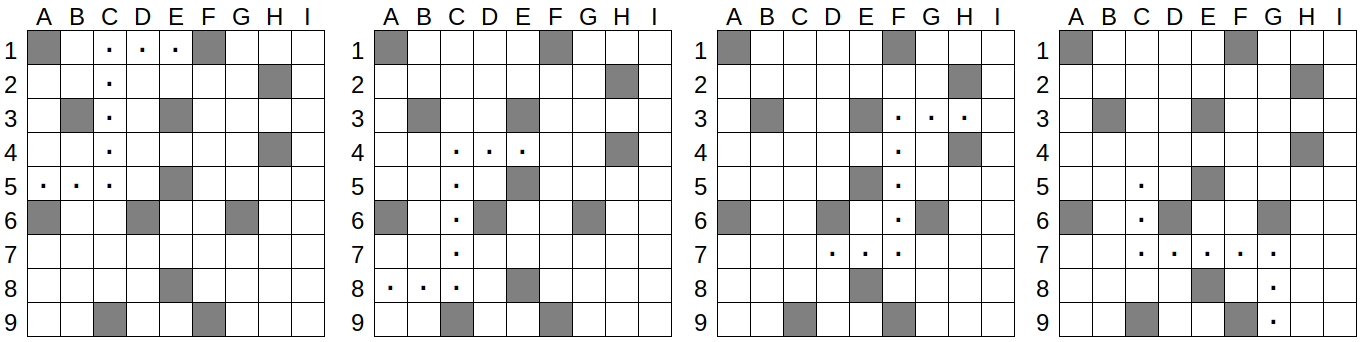
Самый простой способ найти эти пути — это начать с поиска пяти последовательных белых квадратов, а затем попытаться расширить конечные точки в обоих направлениях. Чтобы быть уверенными в результате, мы должны делать это систематически. Например, мы можем начать с верхнего левого угла поля и двигаться к нижнему правому углу. При этом мы должны искать как горизонтальные, так и вертикальные полосы из пяти квадратов.
Путь дрона симметричен. Значит, дрон может стартовать с любого конца каждого из четырех путей. Следовательно, возможных различных квадратов для старта в два раза больше, то есть восемь.
Это задание является простым примером сопоставления с паттерном. Этот метод часто используется в области обработки изображений. Проблема определена паттерном (шаги 1–5) и тестовым полем (то есть изображением для поиска паттерна). Сопоставление с паттерном имеет множество применений. Например, оно используется при распознавании лиц или при анализе медицинских изображений. Во многих методах сопоставление с паттерном описывается в виде траектории, аналогично описанию в этом задании.

Шесть друзей выбирают, какой из семи фильмов посмотреть. Друзья оценивают фильмы так:
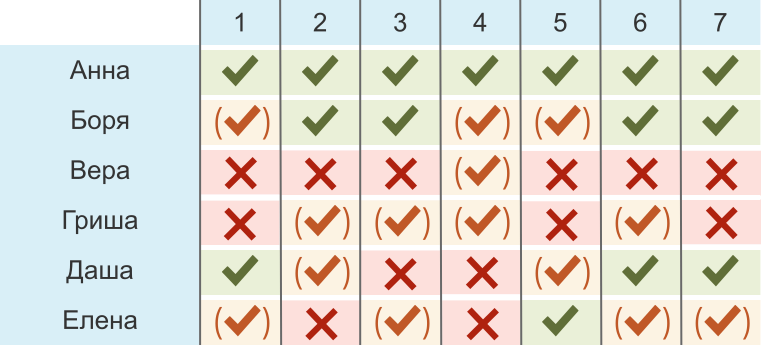
Оценки от лучшего к худшему выглядят следующим образом: 


Фильм становится любимым, если все друзья ставят ему наивысшую оценку среди всех свои оценок. Например, фильм №1 не является любимым фильмом, потому что Вера дала свою лучшую оценку фильму №4.
Каково наименьшее возможное количество изменений оценок, чтобы фильм стал любимым?
[Täisarv]
Правильный ответ: 2.
Невозможно изменить только одну оценку, чтобы один из фильмов в таблице тут же стал любимым. Для каждого фильма было по крайней мере два друга, которые оценили какой-то другой фильм лучше:
| Фильм | Количество людей, которые предпочли другой фильм |
|---|---|
| 1 | 4: Боря, Вера, Гриша и Елена |
| 2 | 3: Вера, Даша и Елена |
| 3 | 3: Вера, Даша и Елена |
| 4 | 3: Боря, Даша и Елена |
| 5 | 4: Боря, Вера, Гриша и Даша |
| 6 | 2: Вера и Елена |
| 7 | 3: Вера, Гриша и Елена |
Теперь нам нужно убедить Веру и Елену, чтобы каждая из них изменила по одной своей оценке таким образом, чтобы фильм №6 стал их любимым. Очевидное решение с двумя изменениями состоит в том, что Вера и Елена могут улучшить свои оценки для фильма №6. Но в качестве альтернативы они могут понизить оценку фильмов, которые они до этого оценили лучше, чем фильм №6. В случае Веры это был бы фильм №4, а в случае Елены — фильм №5. Отметим, что второе решение было бы невозможным, если у одного (или у обоих) друзей было бы более одного фильма оценено выше, чем фильм №6.
Как составить таблицу, необходимую для решения задания?
Один из вариантов — это проверить для каждого фильма и для каждого друга отдельно, оценил ли этот друг какой-нибудь другой фильм лучше. Но является ли такой алгоритм оптимальным? Если у нас есть S друзей и F фильмов, то нам нужно просмотреть все ячейки в таблице размера S*F и сравнить каждую оценку с той оценкой, которую этот друг поставил для остальных фильмов F–1. Действуя таким наивным способом, нам придётся произвести S·F·(F–1) сравнений оценок.
На самом деле, чтобы увидеть, вызывает ли для определенного фильма проблему оценка одного из друзей, достаточно просто знать его наилучшую оценку. Если конкретная оценка ниже общей оценки этого друга, то этот оценённый фильм не может быть любимым. Это означает, что если мы сначала узнаем лучшие оценки каждого друга (изучив F·S оценок), то для всех оценок F·S мы сможем проверить являются ли они ниже, чем лучшая оценка рассматриваемого друга. В итоге, используя такой альтернативный алгоритм, надо будет просмотреть (вместе с предварительным расчётом) 2·F·S оценок.
Если S=6 и F=7, то первому алгоритму понадобится 252, а второму — 84 операций. Оба алгоритма дадут одинаковый результат, но второй алгоритм будет эффективнее первого.
Одним из основных направлений деятельности информатиков является решение задач не только правильно, но и максимально эффективно. Хотя аппаратное обеспечение становится быстрее, от него мало толку, если программисты "съедают" это увеличение скорости неэффективными алгоритмами.

Белла попросила у своей подруги Анны номер телефона. Так как Анна не хочет, чтобы другие знали её номер телефона, то она передала бумажку, где номер телефона был засекречен. Позже Анна объяснила Белле, что номер был закодирован следующим образом:
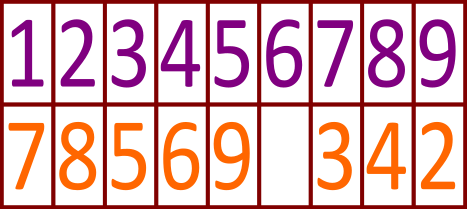
Что из нижеприведённого является номером телефона Анны?
[Raadionupud]
A. 123 456 789
B. 785 691 342
C. 173 592 846
D. 173 859 246
Правильный ответ: C.
Если упорядочить столбцы таблицы по следующим номерам (так, чтобы каждая цифра во 2-ой строке совпадала с цифрой следующего столбца в 1-ой строке), то правильный ответ появится на 1-ой строке.
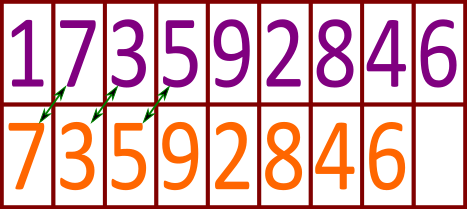
Шифрование личных данных очень важно в нашей жизни. Никто не хочет, чтобы другие узнали его PIN-код или пароль от банковского счёта, никто не хочет, чтобы другие смогли прочитать его переписку. Наши письма, личные данные и деньги в банках должны быть в безопасности. К счастью, компьютеры очень хорошо шифруют сообщения, и информатики усердно работают над поиском новых способов защиты цифровых данных.
К сожалению, разработанные для компьютеров криптографические алгоритмы не подходят для использования, когда речь идёт об информации, которую людям необходимо записать на бумагу или прочитать с бумаги. В этом случае придётся довольствоваться методами, требующими меньших вычислений, но не являющихся настолько безопасными, но всё же защищающие от случайного подглядывания.
В нашем задании цифры номера телефона были сохранены особым образом. Вместо того, чтобы разместить их в том порядке, в котором они появляются в телефонном номере, мы добавили ссылку на каждую из них, чтобы показать, где находится следующая цифра. Подобные используемые в компьютерах структуры называются связанными списками (англ linked list), и они имеют ряд преимуществ. Если мы хотим добавить элемент в этот список между другими элементами, то нам не нужно перемещать другие элементы — достаточно просто изменить две ссылки.

Саша и Питер — соседи: окна их комнат напротив друг друга через улицу. Каждый день они играют в игру: вечером перед сном оба записывают число на бумажке и приклеивают её на своё окно. Утром оба смотрят на число на противоположном окне, прибавляют его к своему числу и прикрепляют к своему окну новую бумажку с полученной суммой. Выигрывает тот, у кого на окне на бумажке оказывается наименьшее число.
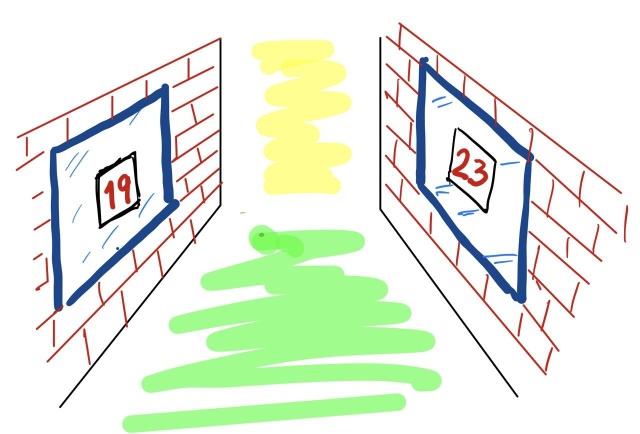
У детей каникулы и они просыпаются в разное время, поэтому окончательные числа на окнах зависят от того, когда каждый из них проснётся. Допустим, что перед сном Саша записал число 19, а Питер — 23. Если бы Саша проснулся раньше Питера, то он бы заменил число 19 на своём окне на число 42. Тогда Питер увидел бы число 42 и приклеил бы на своё окно бумажку с числом 65; следовательно, Саша выиграл бы. Если бы оба проснулись одновременно, то они оба записали бы 42, и игра закончилась бы ничьей.
Предположим, что перед сном Саша записывает число 25, а Питер — число 47.
Какой из следующих вариантов невозможен?
[Raadionupud]
A. Саша запишет 72, и Питер запишет 119; значит, Саша выиграет.
B. Саша запишет 97, и Питер запишет 119; значит, Саша выиграет.
C. Саша запишет 72, и Питер запишет 72; значит, игра закончится ничьей.
D. Саша запишет 97, и Питер запишет 72; значит, Питер выиграет.
Правильный ответ: B.
Вариант B невозможен. Если они проснутся одновременно, то они оба запишут 72. Если Саша проснётся раньше Питера, то Саша запишет 72, а Питер запишет 119. Если Питер проснётся раньше, то он запишет 72, а Саша — 97. Чтобы Саша записал 97 и Питер 119, они оба должны увидеть сумму друга до обновления своего числа, но это невозможно.
Многие компьютерные системы поддерживают параллелизм, когда одновременно выполняется более одного процесса. Когда эти параллельные вычисления изменяют общие переменные, мы должны гарантировать правильный порядок этих обновлений. Например, в системе бронирования билетов на поезд несколько пользователей могут одновременно бронировать билеты. Если количество доступных мест меньше количества запросов на бронирование, то мы должны гарантировать, что ни одно из мест не будет забронировано дважды. Анализировать параллельные вычисления сложно, потому что мы должны изучить все возможные последовательности, в которых могут развиваться отдельные процессы.

На экране компьютера мы видим рисунок лягушки. Однако цвет лягушки неизвестен.

Для изменения цвета у нас имеется четыре программы, но мы можем запустить только одну из них. Мы хотим быть уверенными, что по завершению работы программы мы получим лягушку именно зелёного цвета, вне зависимости от её первоначального цвета.
Какая программ не гарантирует, что в конце её работы лягушка будет зелёного цвета?
[Raadionupud]
A.
Если лягушка красная, то покрась её в жёлтый, в противном случае — в зелёный.
Если лягушка жёлтая, то покрась её в красный.
Если лягушка не жёлтая, то покрась её в зелёный.B.
Если лягушка красная, то покрась её в жёлтый.
Если лягушка не красная, то покрась её в зелёный.
Если лягушка жёлтая, то покрась её в красный, в противном случае — в зелёный.C.
Если лягушка жёлтая, то покрась её в зелёный.
Если лягушка не жёлтая, то покрась её в красный.
Если лягушка красная, то покрась её в зелёный, в противном случае — в жёлтый.D.
Если лягушка жёлтая, то покрась её в зелёный, в противном случае — в красный.
Если лягушка красная, то покрась её в зелёный, в противном случае — в жёлтый.Правильный ответ: D.
При запуске программы А после выполнения первой команды лягушка будет либо жёлтой, либо зелёной. После выполнения второй команды она уже будет либо красной, либо зелёной. Значит, во время выполнения третьей команды действует условие "лягушка не жёлтая", и лягушка окрашивается в зелёный цвет.
При запуске программы B, во время выполнения второй команды должно обязательно действовать условие "лягушка не красная". Следовательно, лягушка окрашивается в зелёный цвет, а следующая за этим третья команда окрашивает её вновь в зелёный.
При запуске программы C, во время выполнения второй команды должно обязательно действовать условие "лягушка не жёлтая". Следовательно, лягушка окрашивается в красный цвет, а следующая за этим третья команда окрашивает её в зелёный.
Если вначале запуска программы D лягушка будет жёлтая, то во время выполнения первой команды она окрашивается в зелёный. Следующее за этим условие "лягушка красная" не действует, и поэтому лягушка вновь окрашивается в жёлтый цвет.
Программируя (если мы говорим об императивных языках программирования), мы можем записать условные предложения строки, которые выполняются в заданной последовательности. Условные предложения в виде "если C, то A, в противном случае B" (англ "if C then A else B") или просто "если C, то A" (англ "if C then A"), на диаграмме выглядят следующим образом:
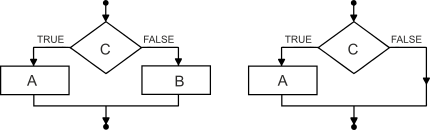
Заметим, что две программы
если C, то A, в противном случае Bи
если C, то A
если не C, то Bкак правило, не являются эквивалентными, то есть они не всегда имеют одно и то же значение. А именно, во втором случае (если условие С проверяется дважды) выполнение команды А может изменить состояние системы таким образом, что условие С становится ложным, а значит запускается как команда А, так и B. В случае первого варианта обязательно выполняется только одна команда из двух (A или B). Это различие мы можем заметить при сравнении вариантов C и D.

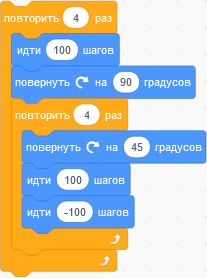
У перемещающегося по полу робота сбоку имеется карандаш. Каждый раз, когда робот двигается, карандаш оставляет линию. Робот стартует с центра белого пола и следует следующим командам:
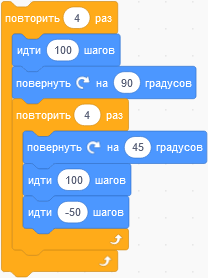
Обратите внимание, что:
Какое из нижеприведённых изображений нарисует такой робот?
[Raadionupud]
A. 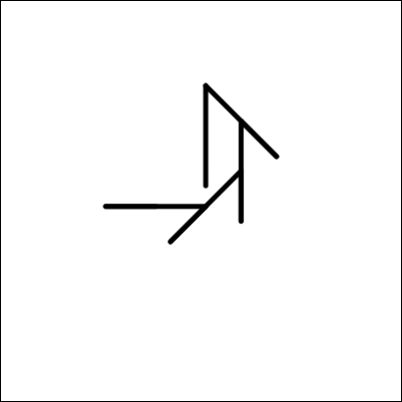
B. 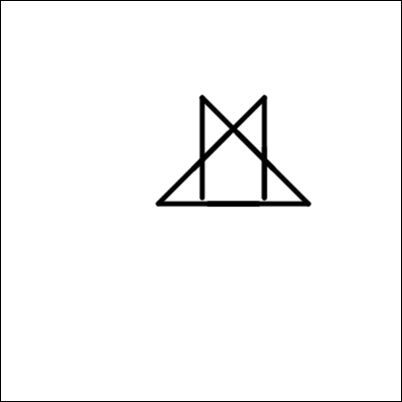
C. 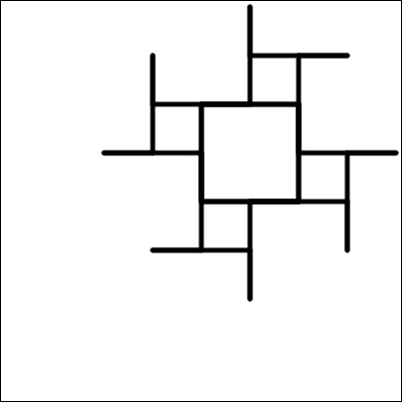
D. 
E. 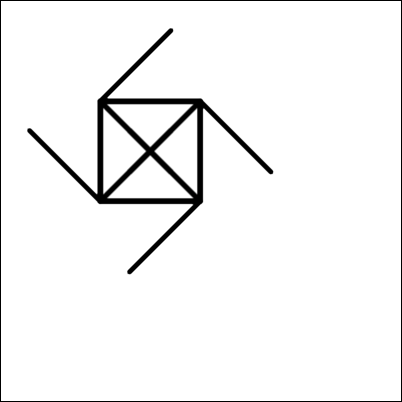
Правильный ответ: D.
Существуют разные способы исключения неправильных ответов и определения правильного ответа. Одним из примеров является подсчёт количества линий — 4 во внешнем цикле и каждый раз, в свою очередь, 4 во внутреннем цикле; всего 16. Однако нужно быть осторожным, если линия рисуется поверх другой. Это ведёт к двум более сложным паттернам (вышеприведённые изображения 3 и 4). Затем мы можем посмотреть на количество поворотов на 45 градусов. Это исключает изображение 3, оставляя изображение 4 в качестве правильного ответа.
Другой способ решить эту проблему — это попытаться самому начертить все изображения, следуя алгоритмам:
| Программа | Результат |
|---|---|
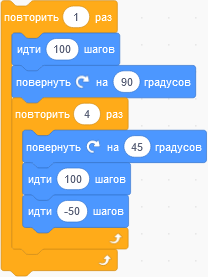 |
 |
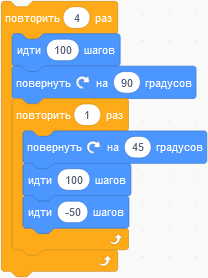 |
 |
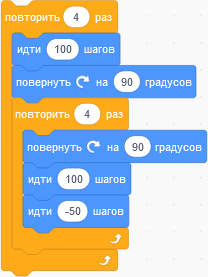 |
 |
 |
 |
Многие паттерны, встречающиеся в природе, создаются многократным повторением очень простых правил. С помощью напольного робота, или так называемой черепашьей графики, этот процесс можно использовать для создания интересующих нас паттернов. В этом задании ясно показывается сила программирования и, в данном случае, повторяющихся блоков кода. Даже некоторые неправильные ответы интересны и могут быть созданы за счёт небольших изменений.
Решение этого задания требует либо разделения программы на части и анализа представленных паттернов, чтобы исключить не соответствующие заданной программе паттерны, либо пошаговое выполнение программы, как если бы мы сами были напольными роботами. Эти обе подходящих техники отладки часто используются программистами для поиска ошибок в своих программах.

В приведённом тексте пробелы отмечены символом '·', а переходы на новые абзацы символом '¶'. Неотмеченные переходы на новую строку автоматически добавляются текстовым процессором.
Логика·—·это·наука·о·правилах·,структурах·и·формах·мышления.
Слово·«логика»·первоначально·происходит·от·древнегреческого·прилагательного·
λογική·(·logikē),·которое·является·женской·формой·λογικός·(logikos;·«относящийся·
к·речи·;·относящийся·к·мышлению»).·Слово·использовалось·либо·как·отдельное·
существительное,либо·во·фразе·λογικὴ·τέχνη(logikē·technē)·в·смысле·«искусство·
мышления».Сколько существует пар слов, между которыми при оформлении текста пробелы были использованы неправильно?
(Если в одной паре допущено несколько ошибок, то считай это за одну ошибку.)
[Täisarv]
Правильный ответ: 5.
Первая ошибка — это 'правилах·,структурах', где пробел должен быть после запятой, а не перед.
Вторая ошибка — это 'λογική·(·logikē)', где пробела не должно быть после скобки.
Третья ошибка — это 'речи·;·относящийся', где пробела не должно быть перед точкой с запятой.
Четвертая ошибка — это 'существительное,либо', где пробел должен быть после запятой.
Пятая ошибка — это 'τέχνη(logikē', где пробел должен быть перед скобкой.
Помимо того, что неправильное использование знаков препинания является ошибкой правила правописания, оно также может привести к неудобствам, связанным с автоматическим переносом строки во время обработки текстов на компьютере. Если не поставить пробел после запятой или точки, то при необходимости текстовой редактор не сделает в этом месте разрыва строки; это может повлиять на выравнивание текста. Если поставить пробел перед запятой или точкой, то при автоматическом переходе на новую строку текстовой редактор может перенести знак препинания в начало следующей строки, а это выглядит некрасиво.
По тем же причинам пробелы ставятся перед открывающей скобкой и открывающими кавычками, а также после закрывающей скобки и закрывающими кавычками, но не после открывающей скобки и открывающих кавычек или перед закрывающей скобкой и закрывающими кавычками.
С точки зрения правописания мы можем обсудить, имеется ли в случае 'правилах·,структурах' одна ошибка (пробел и запятая в неправильном порядке) или две ошибки (лишний пробел перед запятой, отсутствие необходимого пробела после запятой). Чтобы было ясно и понятно, то вместо количества ошибок в задании спрашивается количество пар слов, где что-то не так. Такая же точность требуется во многих ситуациях, когда разные стороны (будь то люди или компьютеры) должны понимать правило одинаково — например, когда оценивание за диктант на экзамене по эстонскому языку основывается на количестве ошибок.

Рассмотрим следующий лист электронной таблицы, где в некоторых ячейках содержатся числа, а в некоторых — формулы:

Имеющаяся на рабочем листе функция SUM вычисляет сумму значений в ячейках заданного диапазона, а функция MAX находит наибольшее (максимальное) значение в ячейках заданного диапазона. Диапазоны ячеек задаются их крайними левыми верхними и крайними правыми нижними ячейками.
Какое значение появится в табличной ячейке C3?
[Täisarv]
Правильный ответ: 21.
Простой способ найти ответ — это вычислить значения во всех ячейках. Так мы получим
B2 = SUM(A1:A3) = A1+A2+A3 = 1+6+7 = 14
B3 = SUM(A2:A4) = A2+A3+A4 = 6+7+8 = 21
B4 = SUM(A3:A5) = A3+A4+A5 = 7+8+4 = 19
C3 = MAX(A1:A3) = MAX(14;21;19) = 21Другой способ — это заметить, что значение в ячейке B3 отличается от значения в ячейке B2 тем, что 1 не учитывается в сумме, но добавляется 8; поэтому значение в ячейке B3 будет больше. Аналогично рассуждая, получим, что значение в ячейке B3 больше, чем значение в ячейке B4. Значит, именно значение В3 является максимальным, которое выбирает расположенная в ячейке С3 формула, и мы можем ограничиться вычислением только этой одной суммы.
Формулы, используемые в рабочих листах электронных таблиц, позволяют автоматизировать повторяющиеся вычисления, экономя время пользователей и уменьшая количество ошибок, вызванных вычислениями вручную.
Системы электронных таблиц также пытаются оптимизировать объём выполняемой работы. Если мы меняем значение в какой-нибудь ячейке, то система пересчитывает значения только тех формул, которые зависят от этой ячейки (а затем те формулы, которые зависят от измененных значений, и т.д.). Метод отличается от того, что мы использовали выше, когда пытались избежать подсчёта сумм, но цель та же: делать как можно меньше ненужной работы. Компьютеры считают быстро, но для очень больших листов с огромным количеством формул экономия все же необходима.

Детективное бюро Бобрики должно выяснить пароли пяти преступников, чтобы получить доступ к их учётным записям. Они уже знают следующее:
Ana99stassia, A40nastassia или Anastassi17a.% & * # ! @ + $), например, Боброград@, Бобробург* или Древорополь!.BRZT, AAAA или EZEZ.amiDen, neimaD или Dnmiea.ElLeNa, ELLena или Ellena.Детективы пытаются выяснить пароли, перебирая один за другим все возможные варианты, соответствующие паттерну каждого преступника. Для этого у них также есть список всех 312 деревень в Кобрастонии.
Чей пароль они, скорее всего, выяснят за наименьшее количество попыток?
[Raadionupud]
A. Анастассии
B. Бруно
C. Веры
D. Дамиэна
E. Эллены
Правильный ответ: E.
Детективы, скорее всего, быстрее всего выяснят тот пароль, для которого существует меньше всего вариантов. Поэтому мы подсчитываем, сколько вариантов есть для каждого пароля.
D, a, m, i, e или n), для второй буквы осталось 5 кандидатов (поскольку из шести возможных букв одну уже выбрали для первой позиции), 4 кандидата для третьей буквы и т.д. Таким образом, всего 6·5·4·3·2·1=720 вариантов.e или E для первой буквы, l или L для второй и т. д. Всего имеется только 2·2·2·2·2·2=64 вариантов.Поэтому у Эллены наименьшее количество вариантов.
Мы подсчитали количество вариантов для всех паролей, но достаточно было бы сделать это только для Эллены и сравнить этот результат в самом общем виде с другими вариантами (например, 90 двузначных чисел, 312 деревень и т. д.).
У этого задания имеется как минимум две связи с информатикой и вычислительным мышлением.
Во-первых, многие люди используют какой-нибудь паттерн, когда им нужно придумать новый пароль. Как видно из этого задания: чем проще паттерн, тем проще кому-то другому методом перебора всех вариантов подобрать пароль. Не забывайте, что компьютеры могут автоматически пробовать пароли, и они это делают намного быстрее, чем люди, и это им не надоедает.
Хороший пароль состоит из множества маленьких букв, больших букв, цифр, специальных символов, например 2kb-C6xV!/<)^-U. Если мы рассмотрим, например, 26 маленьких и 26 больших букв, 10 цифр и 10 специальных символов, то всего получится 7215=7244150201408990671659859968 паролей, состоящих из 15 символов! Есть приложения, которые генерируют такие пароли, а также помогают пользователю их запомнить (точнее, они запоминают эти пароли вместо пользователя).
Еще один хороший вариант, если это позволяет используемая система, — это использовать вместо одного короткого слова состоящую из нескольких слов фразу. Например, correct horse battery staple. Используя словарь с 50000 словами, можно составить 500004=62500000000000000000 таких фраз, которые состоят из четырёх слов. Это меньше, чем в предыдущем примере, но всё же довольно много. В то же время такие фразы гораздо легче запомнить, а значит, они подходят и тогда, когда по каким-либо причинам нельзя использовать приложение для запоминания паролей.
Во-вторых, программист должен уметь оценить, сколько времени вероятнее всего может занять какое-либо вычисление. Информатики называют это «определением вычислительной сложности алгоритмов». Мы использовали слово «вероятный», потому что теоретически возможно, что первый пароль, который мы попробуем, будет правильным, даже в тех случаях, когда существуют миллиарды вариантов. Но может случиться и так, что нам совсем не везёт и мы найдём правильный пароль самым последним. В среднем мы находим правильный пароль на полпути к проверке всех вариантов.

В программировании for-повторение используется для повторения некоторых действий заданное количество раз.
В нижеприведённом примере значения i устанавливаются подряд и ими служат числа 1, 2 и 3, и каждый раз выполняется расположенная в теле команда повторения (часть с отступом); обратите внимание, что в этой команде можно использовать значение i:
for i from 1 to 3
print(i)получим результат
1
2
3Для чисел оператор * (звёздочка) означает умножение, а для текста — его повторение:
for i from 1 to 3
print(i * "x")получим результат
x
xx
xxxКакой паттерн мы получим, если воспользуемся нижеприведённым фрагментом кода?
for i from 1 to 5
print(((6 - i) * 2) * "x")
for i from 1 to 5
print((i * 2) * "x")[Raadionupud]
A.
xxxxxxxxxx
xxxxxxxx
xxxxxx
xxxx
xx
xx
xxxx
xxxxxx
xxxxxxxx
xxxxxxxxxxB.
xxxxxxxxxx
xxxxxxxx
xxxxxx
xxxx
xx
xx
xxxx
xxxxxx
xxxxxxxx
xxxxxxxxxxC.
xx
xxxx
xxxxxx
xxxxxxxx
xxxxxxxxxx
xxxxxxxxxx
xxxxxxxx
xxxxxx
xxxx
xxD.
xx
x x
x x
x x
x x
x x
x x
x x
x x
xxПравильный ответ: A.
Мы можем быстро исключить все остальные варианты, заметив, что программа не печатает пробелы (" "). Вариант ответа А — единственный, который их не содержит.
Представленное здесь for-повторение используется почти во всех языках программирования. Повторы используются, как следует из названия, для многократного выполнения частей программы; for-повторение подходит, когда количество повторений известно заранее.
Использование операторов для разных целей в зависимости от типа данных называется перегрузкой операторов или полиморфизмом. Полиморфизм используется в языках программирования в основном потому, что количество операторов ограничено, а количество возможных операций намного превышает количество доступных операторов.
При перегрузке операторов рекомендуется придавать им значение, как можно более близкое к «нормальному». Таким образом, разумно, что * означает для чисел умножение, а для текста — его повторение; а, например, + для чисел означает сложение, а для текста — их соединение:
print("a" + "b")получим
ab
Цепной код — это экономный способ представления контуров (границ) на чёрно-белых изображениях. Суть заключается в выборе одного чёрного пикселя и сохранении на каждом этапе прохождения контура по движению часовой стрелки направления, которое позволит добраться до следующего чёрного пикселя.
Направления отмечены цифрами следующим образом:
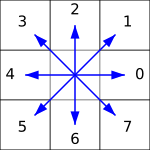
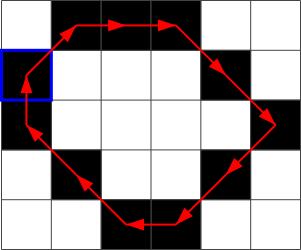
Например, если на нижеприведённом изображении стартовый пиксель отмечен синей рамкой, то дальше можно двигаться в отмеченных красными стрелками направлениях. Как результат, цепной код будет 1, 0, 0, 7, 7, 5, 5, 4, 3, 3, 2.
Рассмотрим теперь такое изображение:

Что из приведённого не будет цепным кодом этого изображения?
[Raadionupud]
A. 1, 1, 1, 0, 7, 7, 7, 6, 5, 5, 5, 4, 3, 3, 3, 2
B. 7, 6, 5, 5, 5, 5, 4, 3, 3, 2, 1, 1, 1, 1, 0, 7
C. 5, 5, 5, 4, 3, 3, 3, 2, 1, 1, 1, 0, 7, 7, 7, 6
D. 3, 3, 2, 1, 1, 1, 0, 7, 7, 7, 6, 5, 5, 5, 4, 3
Правильный ответ: B.
Следующие рисунки демонстрируют получение цепных кодов в вариантах ответов:
A. 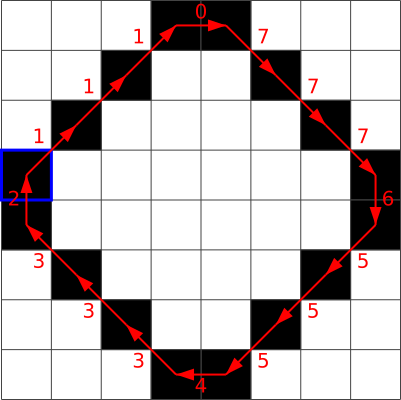 B.
B. 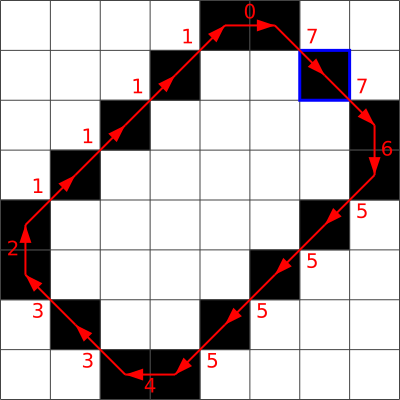
C. 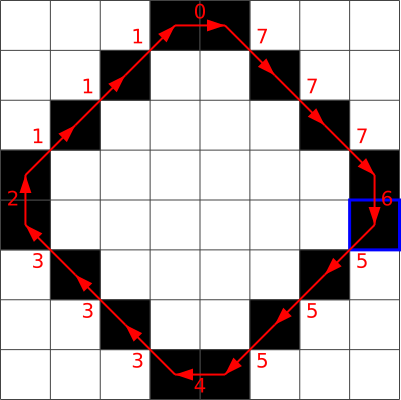 D.
D. 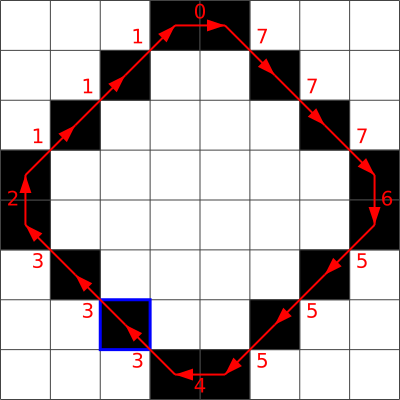
Одной из областей применения цепного кода является распознавание цифр. Во-первых, этот код позволяет представлять объекты более компактно, а во-вторых, проведение сравнения цепных кодов намного легче, чем сравнение изображений. К тому же из цепного кода можно получить единичные свойства изображённого объекта. Цепные коды представляют собой сжатие без потерь и сохраняют всю информацию, необходимую для быстрого и эффективного анализа паттернов.
Copyright © 2022 Bebras – International Challenge on Informatics and Computational Thinking.
Licensed under Creative Commons Attribution-ShareAlike 4.0 International License.
Flag icons by GoSquared.