


Igal aastal paneb Siim oma sünnipäeval tordile küünlad, et näidata nii oma uut vanust. Küünlaid on kolme värvi: oranžid, punased ja sinised. Kõik "0" kujulised küünlad on oranžid, kõik "1" kujulised küünlad punased ja nii edasi (vt tabelit).
| Number | Värv |
|---|---|
| 0 | Oranž |
| 1 | Punane |
| 2 | Sinine |
| 3 | Oranž |
| 4 | Punane |
| 5 | Sinine |
| 6 | Oranž |
| 7 | Punane |
| 8 | Sinine |
| 9 | Oranž |
Täna on Siimul 11. sünnipäev ja seepärast on mõlemad küünlad tordil sama värvi. Ta peab ootama kolm aastat, kuni ta on 14-aastane, enne kui mõlemad küünlad tordil on taas sama värvi. Seejärel tuleb oodata kolm aastat, kuni ta saab 17-aastaseks, ja siis veel viis aastat, kuni ta saab 22-aastaseks.
Kui Siim kasutaks seda süsteemi tänasest kuni 99-aastaseks saamiseni, siis kui kaua peab ta maksimaalselt ootama kahe sünnipäeva vahel, et tema vanuse märkimiseks oleks tordil kaks sama värvi küünalt?
[Raadionupud]
A. 5 aastat
B. 6 aastat
C. 7 aastat
D. 8 aastat
Õige vastus on: A (5 aastat).
Olgu XY inimese praegune vanus, kus X ja Y on kaks numbrit lõigust 0 kuni 9 ning X ja Y on ülesandes oleva tabeli järgi sama värvi. Oletame, et Y on üks arvudest 0, 1, 2, 3, 4, 5 või 6, sel juhul peab ootama kolm aastat vanuseni X(Y+3), et näha kahte sama värvi küünalt.
Järgmisena vaatame eraldi juhtumeid, kus Y on 7, 8 või 9:
Seetõttu on maksimaalne ooteaeg 5 aastat, kunagi ei pea ootama 6 või enam aastat.
Selles ülesandes on kahekohaliste arvude jada kokku pandud värvipaaride jadaga. Selle abstraktse jada n. element on kahe küünla värvid, mida kasutatakse arvu n esitamiseks. Üsna sageli räägitakse arvutiteaduses jada moodustamise reeglitest ja me peame jada simuleerima, kuni teatud tingimused on täidetud.
Selle ülesandega illustreeritud arvutusliku mõtlemise aspektid hõlmavad algoritme, esitust ja mustrituvastust.
Algoritmid: ülesanne on näide algoritmi analüüsimisest. Ülesandes antakse algoritm, mis genereerib värvipaaride jada ehk iga kahekohalise arvu esitamiseks kasutatavate küünalde värvid. Vastuse otsimiseks jada simuleerimise abil kuluks liiga palju aega, seega peame selle asemel analüüsima algoritmi omadusi ning vajadusel kasutama jada lühikeste lõikude simuleerimist.
Esitus: ülesandes on arvud esitatud värvipaaridena (me ütleme, et arvud on vastavusse seatud värvipaaridega). Ülesandes peame pidevalt rakendama seda reeglit erinevatele numbritele, et tuvastada arvud, mida esindab sama värvi küünalde paar.
Mustrituvastus: vähesel määral on ülesanne ka mustrituvastuse näide. Ülesandes antakse muster, mis antud juhul on värviliste küünalde paaridest koosnev jada, kus värve esitatakse lihtsa algoritmi abil.

Tahitil veedetud puhkuse ajal ostsid Moonika ja Veroonika helmeid ja tegid neist endale kaelakeed. Valminud kaelakeed olid sellised:
Moonika:

Veroonika:

Seejärel otsustasid tüdrukud helmeid kaelakeede vahel vahetada järgmiste sammude abil:
Millised näevad Moonika ja Veroonika kaelakeed välja pärast nende sammude sooritamist?
[Raadionupud]
A. 
B. 
C. 
D. 
Õige vastus on: D.
Et näha, miks variant D on õige, jälgime iga tehtud sammu eraldi. Alustame kahe kaelakee algsest seisundist:
Moonika:

Veroonika:

Teeme samme, eemaldades helmeid ükshaaval kummagi kaelakee paremast otsast vaheldumisi, alustades Moonikast. Allolevas selgitavas tekstis viitame terminiga "iteratsioon" sammude 1-3 ühele läbimisele. All on toodud ka joonis, mis näitab iga iteratsiooni järel saadud tulemust. Sellel tähistab esimene värviliste ridade paar kaelakeede algseisundit, sellele järgnevad värviliste ridade paarid kujutavad kaelakeesid pärast iga iteratsiooni.
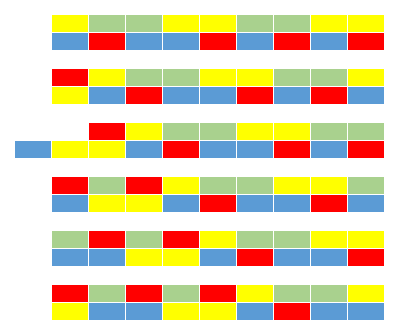
Iteratsioon 1: Kuna mõlema kee parempoolsetes otstes asuvad helmed on kollased või punased, võetakse need ära ja lisatakse sõbranna kaelakee vasakusse otsa. Kumbki on seega ära andnud ühe helme.
Iteratsioon 2: Kuna Moonika kaelakee paremas otsas on kollane helmes, lisab ta selle Veroonika kaelakee vasakusse otsa. Veroonikal on sinine helmes, seega seda ei vahetata, vaid see lisatakse tema enda kee vasakusse otsa. Moonika on nüüd ära andnud kaks ja Veroonika ühe helme.
Iteratsioon 3: Moonika järgmine helmes on roheline, nii lisab ta selle enda kaelakee vasakusse otsa. Veroonika järgmine helmes on punane, selle paneb ta Moonika kee vasakusse otsa. Kumbki on ära andnud kaks helmest.
Iteratsioon 4: Moonika järgmine helmes on roheline, selle lisab ta enda kaelakee vasakusse otsa. Veroonika järgmine helmes on sinine, seega lisab temagi selle enda kee vasakusse otsa. Kumbki on ära andnud kaks helmest.
Iteratsioon 5: Mõlema kee järgmised helmed on kollane ja punane, seega need vahetatakse ja lisatakse teise kee vasakusse otse. Kumbki on nüüd ära andnud kolm helmest.
Kuna kumbki on teisele kinkinud kolm helmest, siis vahetamine peatub ja tulemusena saadud kaelakeed näevad välja nagu alloleval pildil ehk vastusevariandis D.
Moonika:

Veroonika:

Variant A ei saa olla õige, kuna Moonika ja Veroonika pidid loovutama kumbki kolm helmest, selles näites on aga Moonika kees neli punast ja Veroonika omas neli kollast helmest, mida neil enne polnud.
Variant B ei saa olla õige, sest kummagi tüdruku kees on vaid kaks uut värvi helmest.
Variant C pole ka õige. Kuigi erinevat värvi helmeste arv keedes on õige, asetsevad need vales järjekorras.
Selle ülesande abil saame selgitada arvutiteaduse järjekorra mõistet. Järjekord on loend, mille elemente lisatakse ainult ühte otsa ja eemaldatakse ainult teisest otsast. Andme hoidmisel nimetatakse sellist meetodit FIFO-struktuuriks (ingl first in, first out). See on kasulik andmestruktuur, kuna see säilitab elementide lisamise järjekorda.
Moonika ja Veroonika kaelaehteid võib pidada järjekordadeks. Kuigi me ei selgita, kuidas helmed üldse kaelakee külge pandi, selgitavad reeglid, et üks konkreetne ots on ainult uute helmeste lisamiseks ja teine ots ainult nende eemaldamiseks.

Birgit loob "sõnu", kasutades allolevat joonist. Ta alustab alati ringist kirjaga "Algus" ja järgib nooli, kuni jõuab ringi kirjaga "Lõpp". Iga tähe, mida ta seda tehes läbib, kirjutab ta üles.
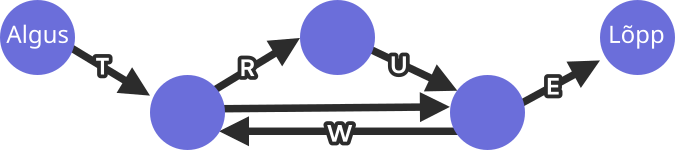
Toodud joonisel on näha, et sel viisil saab ta koostada näiteks sõnu "TRUE" või "TWWWE".
Kui palju erinevaid 8-tähelisi sõnu saab Birgit sel moel koostada?
[Täisarv]
Õige vastus on: 9.
Paneme esmalt tähele, et Birgit peab sõnu alustama alati "T"-tähega ja lõpetama "E"-tähega. Seega otsime me nende kahe tähe vahele kuuetähelisi järjendeid, mis koosnevad tähtedest "R", "U" ja "W".
Edasi märkame, et "T"-noole lõpust "E"-noole algusse saab ta liikuda kas tähepaari "RU" või üldse mitte midagi väljastades, tagasi aga ainult "W"-tähte väljastades. Et mitte ühtki võimalus kahe silma vahele jätta, vaatame nende liikumisviiside kombineerimise võimalusi süstemaatiliselt:
Seega saab Birgit moodustada kokku 1+5+3=9 erinevat sõna.
Kõigi võimaluste läbivaatamine on tegevus, milles arvuti on tõesti võimekas. Praegusel juhul püüame me kõik sobivad sõnad üles kirjutada, pidades samal ajal silmas, et loodud sõnad ei korduks. Toodud on algoritmiline "masin", mis genereerib teatud piirangutega tähejadasid. Selliseid süsteeme kasutatakse mõnikord viktoriinil Kobras osalejatele paroolide genereerimisel või autodele numbrimärkide tootmisel ehk üldiselt sellistel juhtudel, kus on vaja unikaalseid märgijadasid, mis peavad järgima etteantud vormingut. Samas on sageli vaja kontrollida, kas valitud mustri järgi on võimalik koostada piisavalt palju erinevaid sõnu.

Joonisel on veskid ja neid jahuhoidlaga ühendavad teed. Igal õhtul jahvatavad kopraveskid jahu, mis pannakse kottidega veskite ette. Kobras Villi peab kõik kotid kokku korjama ja enne päikeseloojangut hoidlasse tooma. Villi võib kanda ka mitut kotti korraga, kui nende kogukaal ei ole üle 15 kg. Joonisel on näidatud ka Villil iga teelõigu läbimiseks kuluv aeg.
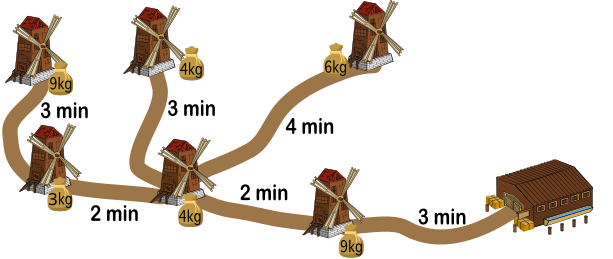
Villi alustab hoidlast ja tahab kõik kotid võimalikult kiiresti hoidlasse kokku kanda.
Mitu minutit tal selle ülesande täitmiseks minimaalselt kulub?
[Raadionupud]
A. 31 minutit
B. 44 minutit
C. 50 minutit
D. 54 minutit
Õige vastus on: C (50 minutit).
Jahu kaal kõigis kottides kokku on 35 kg. Kuna Villi võib igal retkel kanda maksimaalselt 15 kg, siis peab ta kõigi kottide hoidlasse toomiseks ette võtma vähemalt kolm retke. Oma aja minimeerimiseks peaks ta ühe retke ajal korjama kotte võimalikult paljudest lähestikku asuvatest veskitest.
Näiteks koos 9 kilo kaaluva kotiga ülemisest vasakpoolsest veskist saab Villi kaasa võtta ka 3-kilose koti naaberveskist (kogukaal 12 kg). Kõik teised kotid kaaluvad üle 3 kilo, seega ei saa ta samal retkel rohkem kotte oma koormasse lisada. See retk kestab 3+2+2+3+3+2+2+3=20 minutit.
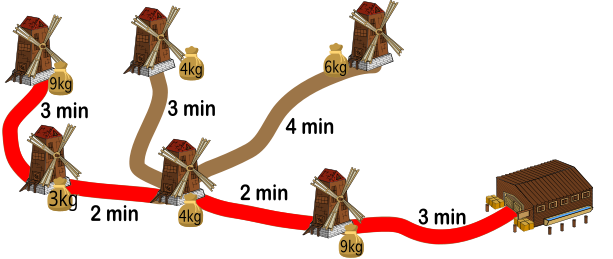
Teisel retkel saab ära tuua kolm kaugemat neljast allesjäänud kotist: 6 kilo kaaluv kott ülemisest parempoolsest veskist ja kaks 4-kilost kotti kahest keskmisest veskist (kogukaal 14 kg). See retk kestab 3+2+4+4+3+3+2+3=24 minutit.
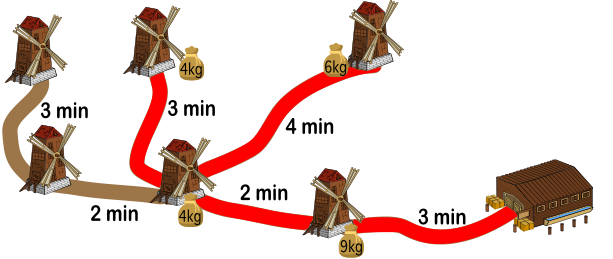
Kolmanda retke ajal toob Villi ära järelejäänud 9 kilo kaaluva koti hoidlale lähimast veskist. Selleks kulub tal 3+3=6 minutit.
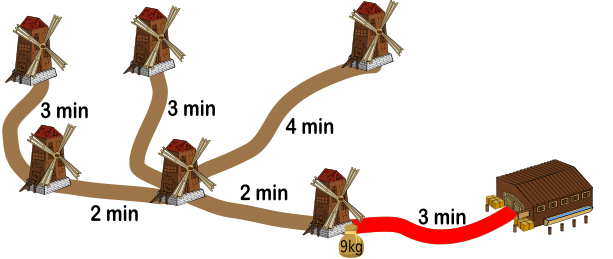
Seega kulub kõigi kottide hoidlasse toomiseks kokku 20+24+6=50 minutit.
Ülaltoodud retkede järjekorda võib muuta, oluline on vaid kottide mõistlik grupeerimine.
Variant A ei saa kindlasti olla õige, sest 9-kilose koti toomine ülemisest vasakpoolsest veskist võtaks juba 20 minutit (ükskõik, kas selle kõrval olev 3-kilone kott ka võtta või mitte). Ülejäänud 10 minutist piisab vaid teise veski juurde ja tagasi liikumiseks, nii et Villi ei jõuaks enam kahte kotti ülemistest veskitest ära korjata.
Ka variant B ei saa olla õige, sest 44 minutit on täpselt esimeseks ja teiseks retkeks kokku kuluv aeg, aga lähimas veskis olevat 9-kilost jahukoti ei saa neile kummalegi lisada.
Variant D ei ole õige vastus, kuna me juba teame, et leidub ka väiksema ajakuluga lahendus.
Informaatikas nimetatakse optimeerimisülesanneteks selliseid ülesandeid, mille eesmärk on leida parim lahendus kõigi võimalike lahenduste hulgast. Tavaliselt on see seotud mingi funktsiooni suurima või vähima väärtuse leidmisega, näiteks selles ülesandes palutakse meil leida kõige väiksem koguaeg. Ka ülesannete lahendamine arvuti abil on sageli seotud optimeerimisega. Sageli soovime, et arvuti saaks tööga hakkama võimalikult lühikese ajaga või kasutades minimaalselt mingit muud ressurssi, näiteks mälu.
Selles ülesandes võime me leida parima lahenduse, proovides ise või arvuti abiga läbi kõikvõimalikud marsruudid ja valides nende hulgast kõige lühema ajaga variandi. Seda meetodit tuntakse toore jõu (ingl brute force) või ammendava läbivaatuse (ingl exhaustive search) tehnikana. See tehnika sobib väikeste probleemide korral (antud juhul pole veskite ja teelõikude arv suur). Kui probleem on suur, töötab toore jõu tehnika väga aeglaselt, kuna võimalikke variante on lihtsalt liiga palju. Seetõttu on olemas teisi tehnikaid, mis suudavad paljudele probleemidele efektiivsemalt lahendusi leida, näiteks ahned algoritmid (ingl greedy algorithm) ja dünaamiline plaanimine (ingl dynamic programming).
Paljude ülesannete täpseks lahendamiseks pole teada ammendavast läbivaatusest efektiivsemat meetodit. Kui mõnda sellist ülesannet on vaja lahendada suure hulga andmete jaoks, tuleb sageli leppida ligikaudsete meetoditega, mis ei tarvitse küll leida kõige paremat lahendust, aga annavad sageli praktikas kasutamiseks piisavalt hea tulemuse.

Bertal ja Laural on oma restoran. Berta edastab toidutellimused Laurale, kasutades lehe- ja lillekujulist signaallampi. Iga roog nende menüüs on varustatud unikaalse koodiga, mis moodustub nendest kahest kujundist. Berta lülitab lambid sisse ja välja järjekorras, mis vastab tellimuse koodile, ja Laura valmistab sellele vastavalt söögi.
Alguses leppisid Berta ja Laura kahele roale oma restorani menüüs kokku sellised koodid:
| Roog | Kood |
|---|---|
| Burger |   |
| Praetud riis |    |
Probleem oli selles, et Laura alustab toiduvalmistamisega kohe, kui ta saab aru, et saadud kood vastab mingile menüüs olevale roale. Kui Berta lülitas praetud riisi koodi algusena kaks korda põlema lehekujulise lambi, hakkas Laura selle asemel juba burgerit valmistama, seega praetud riis ei valminud kunagi.
Probleemi lahendamiseks otsustasid nad koode muuta. Täielik menüü uute koodidega on selline:
| Roog | Kood |
|---|---|
| Burger |   |
| Praetud riis |     |
| Võileib |   |
| Pitsa |    |
| Kook |    |
Nüüd tahavad nad lisada menüüsse ka friikartulid.
Millist järgnevatest koodidest võiks kasutada friikartulite tellimiseks?
[Raadionupud]
A. 


B. 


C. 


D. 



E. 



Õige vastus on: A.
Laura hakkab valmistama vale rooga, kui selle täielik kood on samasugune mõne teise koodi esimese osaga. Seetõttu ei tohi ühegi roa koodi algus sisaldada ühegi teise roa täielikku koodi.
Variant B ei ole seega õige vastus, sest burgeri täielik kood on identne variandi B algusega.
| Roog | Kood |
|---|---|
| Burger |   |
| Variant B |    |
Sama kehtib ka koogi ja variandi D ning pitsa ja variandi E kohta.
| Roog | Kood |
|---|---|
| Kook |    |
| Variant D |     |
| Roog | Kood |
|---|---|
| Pitsa |    |
| Variant E |     |
Ka variant C ei ole sobiv lahendus, sest variandi C täielik kood on identne praetud riisi koodi algusega.
| Roog | Kood |
|---|---|
| Praetud riis |     |
| Variant C |    |
Variant A on õige vastus, kuna selle täielik kood ei ole samasugune ühegi teise koodi algusega ja ühegi teise roa täielik kood ei ole identne variandi A koodi algusega.
Laura ja Berta vajavad kodeerimisreeglit, kus ükski täielikest koodidest ei ole ühegi teise koodi algus. Selle omadusega koode nimetatakse prefikskoodideks (ingl prefix code). Informaatikas kasutatakse neid andmete esitamiseks paljudes kohtades.
Lihte viis prefikskoodi saamiseks on anda kõigile kodeeritavatele objektidele ühepikkused erinevad koodid. Näiteks ingliskeelsete tekstide esitamiseks kasutatakse sageli ASCII-koodi, kus igale tähele vastab 7-bitine (7-kohaline numbritest 0 ja 1 koosnev) kood. Selline lihtne meetod on aga sageli ebaefektiivne.
Kavalam lahendus on anda sagedamini esinevatele tähtedele lühemad koodid, nii võtavad sõnad kodeerimisel vähem ruumi. Tähti saab kodeerida erineva pikkusega bitijadadega, aga seda eeldusel, et poleks ühtki tähte kodeerivat bitijada, mis oleks ühesugune mõnd teist tähte kodeeriva bitijada algusega. Näiteks kui "a" on kõige sagedasem täht, millele järgneb "e" ja sellest palju harvamini esinev "d", võiksime kasutada 0 "a" kodeerimiseks, 10 "e" jaoks ja 110 "d" jaoks. Kui me sel viisil kodeerime sõna "aed", saame 010110. Kuna see on prefikskood, saame teksti kodeeritud bitijadast üheselt taastada ja 010110 dekodeeritakse alati kui "aed". Kui oleksime sama sõna kodeerinud ASCII-kodeeringus, oleks see mälus ruumi võtnud 6 biti asemel 3x7=21 bitti. Sellist ideed kasutavad näiteks mõned andmete pakkimise programmid.

Annel on tööl 3 kolleegi, kes jagavad võrgus sama printerit, mis on paigutatud nende töölaudade lähedusse. Kui üks kolleegidest saadab dokumendi printerisse, siis see käivitub ja prindib kogu dokumendi. Kui ühe dokumendi printimise ajal saadetakse printerisse ka mõni teine dokument, lõpetab printer kõigepealt poolelioleva dokumendi ja alustab alles siis uut.

Täna on kontoris kiire päev ja vaja on printida palju erineva pikkusega dokumente. Järgnevates tabelites on iga kolleegi kohta näidatud iga dokumendi printerisse saatmise aeg ja selle dokumendi printimiseks kuluv aeg. Kui dokumendi printimine algab kell 10:00 ja kestab 2 minutit, siis printimine lõpeb kell 10:02. Kahe järjestikuse prinditöö vahel pole mingit ooteaega vaja ja printer saab järgmise dokumendi printimist alustada kohe kell 10:02.
Kolleeg Berta:
| Töö nr | Saatmise aeg | Kestus |
|---|---|---|
| 11 | 10:00 | 2 min |
| 12 | 10:03 | 1 min |
| 13 | 10:10 | 5 min |
Kolleeg Eduard:
| Töö nr | Saatmise aeg | Kestus |
|---|---|---|
| 21 | 10:01 | 1 min |
| 22 | 10:04 | 3 min |
| 23 | 10:12 | 1 min |
Kolleeg Karl:
| Töö nr | Saatmise aeg | Kestus |
|---|---|---|
| 31 | 10:05 | 3 min |
| 32 | 10:08 | 5 min |
| 33 | 10:13 | 1 min |
Millises järjekorras dokumendid prinditakse ja mis kell printer kõigi dokumentide printimise lõpetab?
[Raadionupud]
A. 11 12 13 21 22 23 31 32 33, lõpuaeg on 10:22
B. 11 21 12 22 31 32 13 23 33, lõpuaeg on 10:14
C. 11 12 13 21 22 23 31 32 33, lõpuaeg on 10:14
D. 11 21 12 22 31 32 13 23 33, lõpuaeg on 10:22
Õige vastus on: D.
Allolevas tabelis on näidatud tööde järjekord ja iga dokumendi printimise aeg:
| Töö nr | Saatmise aeg | Alguse aeg | Kestus | Lõpu aeg |
|---|---|---|---|---|
| Töö 11 | 10:00 | 10:00 | 2 min | 10:02 |
| Töö 21 | 10:01 | 10:02 | 1 min | 10:03 |
| Töö 12 | 10:03 | 10:03 | 1 min | 10:04 |
| Töö 22 | 10:04 | 10:04 | 3 min | 10:07 |
| Töö 31 | 10:05 | 10:07 | 3 min | 10:10 |
| Töö 32 | 10:08 | 10:10 | 5 min | 10:15 |
| Töö 13 | 10:10 | 10:15 | 5 min | 10:20 |
| Töö 23 | 10:12 | 10:20 | 1 min | 10:21 |
| Töö 33 | 10:13 | 10:21 | 1 min | 10:22 |
Printer kasutab dokumentide haldamiseks andmestruktuuri, mida nimetatakse järjekorraks (ingl queue). Järjekord on abstraktne andmestruktuur, kuhu andmeid lisatakse ühest otsast ja võetakse välja teisest otsast. Järjekorras olevatest elementidest saab vaadata ainult seda, mis asub järjekorra alguses ja mis sealt järgmisena välja võetakse.
Täpsemalt saab järjekorraga teha järgmisi toiminguid:
Need toimingud on sarnased näiteks kaupluse järjekorraga. Uued ostjad tulevad järjekorra lõppu ja neid teenindatakse saabumise järjekorras. Sellepärast öeldakse ka, et järjekord on FIFO-tüüpi (ingl first in, first out) struktuur. Ka informaatikas kasutame järjekorda siis, kui peame töötlema teavet selle tekkimise või saabumise järjekorras, näiteks sõnumite esitamisel vestlussüsteemis või andmete edastamisel arvutivõrgus.

Väike Kobras kavandab sünnipäevapidu. Ta koostab nimekirja nendest ülesannetest, mis tuleb enne pidu ära teha.
| Ülesanne | Eelnevad ülesanded |
|---|---|
 Külaliste arvu selgitamine Külaliste arvu selgitamine |
 |
 Toidu ostmine Toidu ostmine |
  |
 Kuupäeva valimine Kuupäeva valimine |
- |
 Kulude kokkuarvestamine Kulude kokkuarvestamine |
   |
 Peokoha valimine Peokoha valimine |
 |
Ta mõistab, et enne mõne ülesande juurde asumist tuleb tal täita mõned teised ülesanded, näiteks enne külaliste arvu teadasaamist peab ta valima peo kuupäeva.
Milline järgmistest variantidest on ülesannete täitmiseks õige järjekord?
[Raadionupud]
A.  →
→  →
→  →
→  →
→ 
B.  →
→  →
→  →
→  →
→ 
C.  →
→  →
→  →
→  →
→ 
D.  →
→  →
→  →
→  →
→ 
Õige vastus on: C.
Kui paneme ülesandeid kujutavad ringid joonisele variandi C järjekorras ja tõmbame noole igalt eelnevalt ülesandelt järgnevale, näeme, et kõik nooled osutavad vasakult paremale. See näitabki, et variant C on õige järjekord.
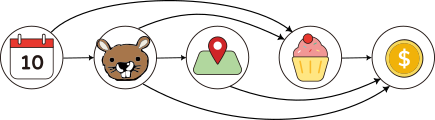
Variandid A ja B ei saa õiged olla, sest kobras peab valima kuupäeva, enne kui saab teada, kui palju külalisi on tulemas. Samuti pole võimalik variant D, sest enne kulude kokkuarvestamist tuleks selgeks teha, kui palju tuleb külalisi.
Sellist tegevuste järjestamist nimetatakse topoloogiliseks järjestamiseks (ingl topological sorting). Arvutile on kõige lihtsam andmete järjestamine numbrilises järjekorras. Kui aga järjestatavatel elementidel puuduvad numbrilised tunnused või kui tahame neid sortida mittenumbriliste tunnuste alusel, peame määrama iga elemendi koha võrreldes teiste elementidega. Sageli saame järjestuse esitamiseks kasutada sellist skeemi, nagu vastuse selgituses oleval joonisel. Arvutiteaduses nimetatakse niisuguseid skeeme graafideks (ingl graph).
Topoloogilist järjestamist kasutatakse tööde või ülesannete planeerimisel igapäevaselt ka tavaelus, sageli isegi selle peale mõtlemata. Lihtne näide on riietumine, kus pesu tuleb selga panna enne teisi riideid ja sokid jalga enne saapaid, aga mütsi ja saabaste omavaheline järjekord pole oluline.

Õpetaja Kobras soovib korraldada oma seitsmele õpilasele filmiõhtu. Selleks kasutab ta kooli koosolekuruumi, kus on ovaalne laud.
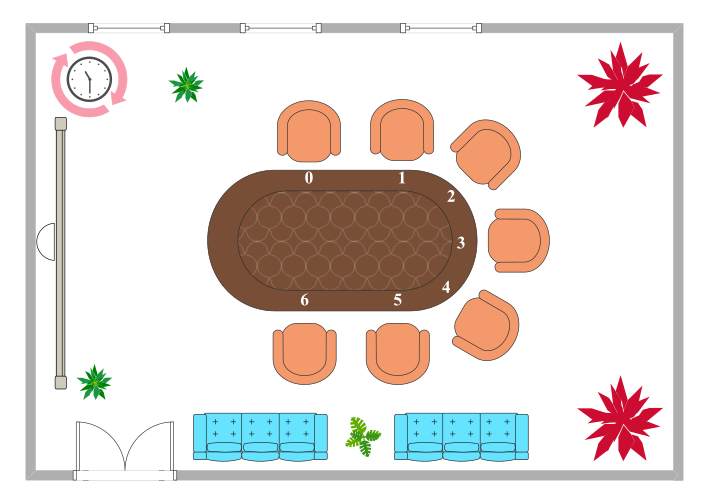
Istekohtade jagamiseks koostas õpetaja järgmised reeglid:
Sünnipäevareegel: iga õpilane istub toolile, mille number on tema sünnipäeva ja sünnikuud tähistavate arvude summa; kui summa on 7 või suurem, näitab tooli numbrit jääk, mis saadakse summa jagamisel seitsmega. Näiteks antakse Jaanile tool number 1, sest tema sünnipäev on 24.12 ning 24+12=36 ja 36 jagamisel seitsmega tekib jääk 1.
Kattumisreegel: kui õpilasele sünnipäevareegli järgi määratud tool on juba hõivatud, tuleb tal liikuda järgmise tooli juurde. Näiteks kui tool 2 on hõivatud, liigub õpilane tooli number 3 juurde, aga kui hõivatud on nii tool 2 kui ka tool 3, liigub ta toolini number 4. Kui hõivatud on tool 6, liigub õpilane edasi tooli 0 juurde.
Tabelis on toodud õpilaste sünnipäevad nende ruumi sisenemise järjekorras:
| Nimi | Sünnipäev |
|---|---|
| Mari | 05.01 |
| Harri | 08.02 |
| Emili | 30.01 |
| Joonas | 09.09 |
| Jaan | 24.12 |
| Moonika | 16.04 |
| Saara | 02.12 |
Millisele toolile istub Saara?
[Raadionupud]
A. Tool nr 0
B. Tool nr 4
C. Tool nr 2
D. Tool nr 5
Õige vastus on: C (tool nr 2).
Õpilased istuvad, nagu näha alloleval joonisel:
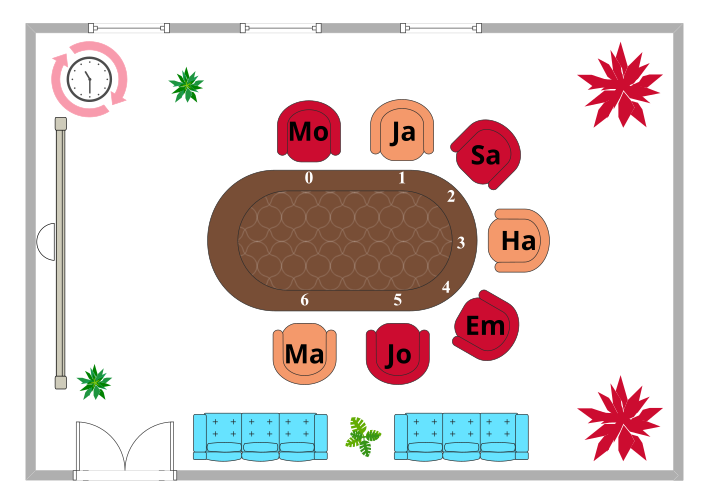
Tooli oranž värv tähistab, et õpilane kasutab seda ilma kattumisreeglita. Tooli punane värv tähendab seda, et õpilane liikus enne vaba koha leidmist edasi vähemalt ühe tooli võrra.
Selleks, et selline istekohtade plaan koostada, tuleb kõigepealt arvutada sünnipäeva ja sünnikuud tähistatavate arvude summad ning seejärel nende summade jäägid 7-ga jagamisel.
| Nimi | Sünnipäev | Summa | Jääk |
|---|---|---|---|
| Mari | 05.01 | 6 | 6 |
| Harri | 08.02 | 10 | 3 |
| Emili | 30.01 | 31 | 3 |
| Joonas | 09.09 | 18 | 4 |
| Jaan | 24.12 | 36 | 1 |
| Moonika | 16.04 | 20 | 6 |
| Saara | 02.12 | 14 | 0 |
Tabelist on näha, et Mari ja Moonika peaks mõlemad istuma toolil 6, kuid seal saab istuda ainult üks neist. Mari istub esimesena ja Moonika peab seega minema teisele kohale.
Kõigi õpilaste kohad saame teada, kui vaatame õpilasi sisenemise järjekorras ja leiame igaühele esimese vaba koha, alustades tabelis näidatud numbriga toolist ja liikudes laua ümber päripäeva (kellaosuti liikumise suunas).
Sellist meetodit kasutatakse informaatikas sageli, kui on vaja andmeid ühtlaselt laiali jagada. Üks näide on failide salvestamisel arvuti kettale neile sobiva koha leidmine. Selline lähenemine on efektiivne ka salvestatud failide hiljem kettal üles leidmiseks. Seda meetodit nimetatakse räsimiseks (ingl hashing).
See ülesanne on ka näide moodularitmeetikast (ingl modular arithmetic), kus tavalise liitmis- või korrutustehte tulemusel saadud vastuse asemel arvestatakse jääki, mis tekib vastuse jagamisel mingi arvuga (nn mooduliga). Selles ülesandes on mooduliks 7. Tuntud moodularitmeetika näited on 12- või 24-tunnine ajaarvestus. Näiteks kui praegu on kell 10 hommikul, siis 4 tunni pärast on see 24-tunni süsteemis väljendatuna 10+4=14, aga 12-tunni süsteemis ütleme, et kell on 2 päeval. Selle põhjus on, et 14 annab 12-ga jagades jäägi 2. Mooduli 7 järgi arvutades saame leida, mis nädalapäev on näiteks 10 või 12 päeva pärast.


Kopra-Daisyle saadeti kingituseks joonistatud süda. Seda tegi ilmselt üks tema neljast parimast sõbrast. Iga sõber ütles ühe lause:
Neil neljal on aga selline imelik komme, et alati räägib tõtt täpselt üks neist.
Kes saatis joonistuse?
[Raadionupud]
A. Jaan
B. Taavi
C. Kaarel
D. Robert
Õige vastus on: D (Robert).
Kuna me teame, et täpselt üks neljast väitest vastab tõele, saatis joonistuse kindlasti Robert.
See ülesanne on loogikaprobleem. Kasutame esmalt dekompositsiooni ehk jagame keerulise probleemi väiksemateks, paremini analüüsitavateks osadeks. Näiteks võime alamülesandena käsitleda ülesannet, milline toodud väidetest on tõene. Seejärel vajame abstraheerimist, et jätta kõrvale ebavajalik info ja keskenduda olulistele faktidele. Eeldame näiteks, et mingi väide on tõene, võtame arvesse selle jaoks olulist teavet ja ignoreerime kõike muud. Seega keskendume korraga ühele väitele, kasutame seejärel väitega seotud teavet ja vaatame, kas leiame teistes viidatud väidetes vastuolusid.
Neli sõpra esitavad lihtsaid väiteid. Kõik need väited e laused võivad olla ainult tõesed või väärad. 1847. aastal sõnastas George Boole võimalused, kuidas selliste lihtsate väidete tõepärasust arvesse võtta. Tema poolt loodud lausearvutus (ingl propositional calculus) ütleb meile, kuidas konstrueerida olemasolevatest tõestest väidetest uusi tõeseid väiteid, arvestamata nende tegelikku tähendust. Ka arvutid töötavad samasuguse loogikaga: väikseim teabeühik e bitt on nagu väide, kuna see võib kanda ainult kahte erinevat väärtust (vastavalt tõene või väär). Lausearvutus on digitaalarvutite ja informaatika tohutu edu alus.

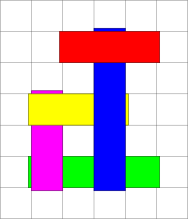
Miia valmistas kooliprojekti jaoks ette kollaaži, asetades paberiribasid järjest üksteise peale.
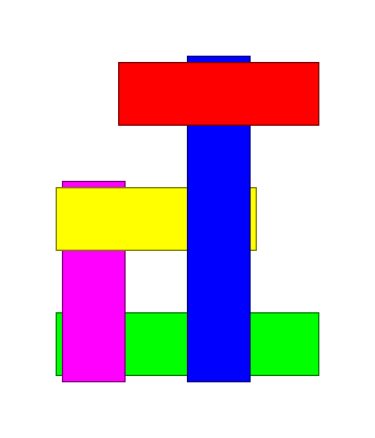
Miia noorem õde Laura tahtis teha samasugust, kuid õe kollaaži kätte võttes kukkusid paberiribad lauale laiali, ainult roheline riba jäi oma kohale. Laura tahab nüüd paberiribad üksteise peale tagasi panna täpselt samamoodi nagu alguses. Aita Laural seda teha, et Miia ei saaks aru, mis on juhtunud.
Millises järjekorras peaks Laura ribad tagasi panema?
[Raadionupud]
A. Lilla, kollane, sinine, punane
B. Punane, sinine, kollane, lilla
C. Kollane, lilla, sinine, punane
D. Lilla, sinine, kollane, punane
Õige vastus on: A (lilla, kollane, sinine, punane).
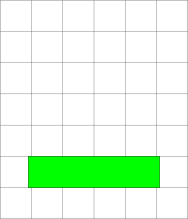
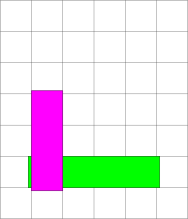


Arvutigraafikas kasutatakse sageli kujutiste joonistamist kihtide kaupa. Sel juhul kustutavad hiljem joonistatud "pealmistes" kihtides olevad kujundid osaliselt või täielikult ära nende alla jäävad varem joonistatud "alumistes" kihtides olevad kujundid. Kujundite joonistamise järjekorraga saab ekraanil tekitada ruumilisi efekte, kus tundub, et mingid objektid on teiste taga.
Kehtib ka vastupidine loogika. Nii nagu selles ülesandes tuli ribade kattumise põhjal aru saada, millised neist olid kollaažis pealpool ja millised allpool, tuleb ka näiteks isesõitvates autodes kahemõõtmelise videopildi põhjal otsustada, millised ümbritseva ruumi objektid on lähemal ja millised kaugemal. Autod peavad lisaks veel aru saama, millises suunas ja kui kiiresti teised objektid nende ümber liiguvad. Sellega tegelevat arvutiteaduse valdkonda nimetatakse raalnägemiseks (ingl computer vision).

Madis otsib väga pikalt veebilehelt oma sõbra telefoninumbrit. Ta pole kindel, kuidas sõbra nime täpselt kirjutatakse, seepärast kasutab ta otsimisel erimärke:
| Märk | Tähendus |
|---|---|
| ? | täpselt üks tundmatu täht |
| & | täpselt kaks järjestikust tundmatut tähte |
| % | mistahes arv tundmatuid tähti kuni nime lõpuni |
Näiteks otsing "Ma%" leiaks nimed Madis, Marta jne.
Millised järgnevatest nimedest leiab otsing "S?rah B&cht%"?
(Märgi kõik õiged vastused.)
[Märkeruudud]
A. Sarah Birchtree
B. Sara Benchton
C. Sarah Bilchman
D. Sirah Beachtram
Õige vastus on: A, D.
Variant A on õige, sest nimi "Sarah Birchtree" vastab otsingule "S?rah B&cht%":
Variant B ei ole õige, sest eesnimes "Sara" ei ole "h"-tähte.
Variant C ei ole õige, sest perenimes "Bilchman" on "cht" asemel "chm".
Variant D on õige, sest "S" ja "S", "i" ja "?", "rah" ja "rah", tühik ja tühik, "B" ja "B", "ea" ja "&", "cht" ja "cht" ning "ram" ja "%" kõik vastavad.
Paljud infosüsteemid võimaldavad info otsimiseks kasutada selles ülesandes kirjeldatud erimärkidele sarnaseid nn metamärke (ingl wildcard) ehk jokkereid. Näiteks nii Windowsi, MacOSi kui Linuxi paljudes käskudes on võimalik mitme faili korraga nimetamiseks kasutada "?" tähenduses "täpselt üks tundmatu märk" ja "*" tähenduses "mistahes arv tundmatuid märke".
Teise näitena lubavad paljud tekstitöötlusprogrammid teksti otsimisel ja ka asendamisel kasutada mustrite kirjeldamiseks nn regulaaravaldisi (ingl regular expression).
Sellised vahendid võimaldavad aega kokku hoida, sest nii saab käske rakendada korraga paljudele failidele või sõnadele. Ilma nendeta tuleks käsk anda kas iga faili või iga võimaliku sõna kohta eraldi.

Kobras Brunol on arvutustabelis andmed ja valemid.

Nüüd hakkab ta valemitega arvutatud väärtustest (real 3) diagramme joonistama.
Millist allolevatest diagrammidest ta nende andmete põhjal kindlasti ei saa?
[Raadionupud]
A. 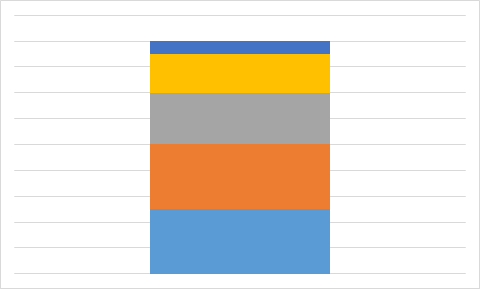
B. 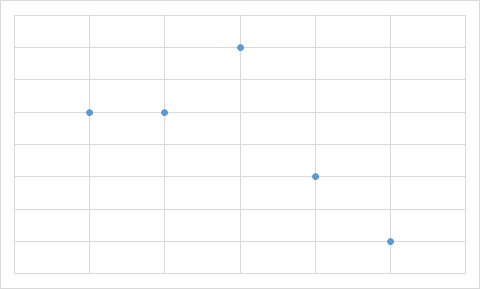
C. 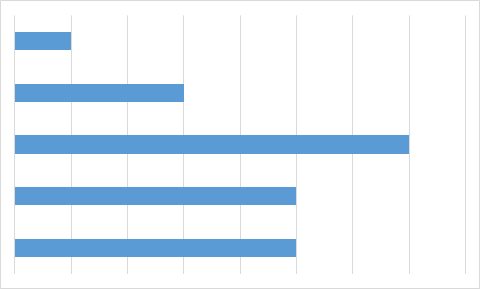
D. 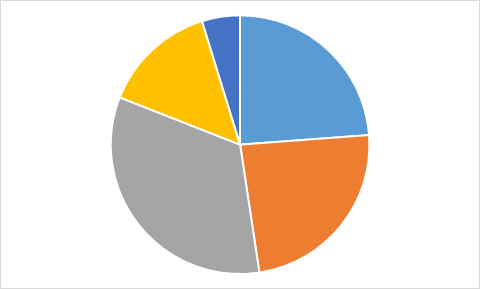
Õige vastus on: A.
Vastuse leidmiseks pole isegi vaja kõigi valemilahtrite väärtusi välja arvutada. Piisab tähelepanekust, et kolmel diagrammil on üks väärtus kõige suurem ja selle järel suuruselt teisi väärtusi kaks võrdset, aga diagrammil A on just maksimaalse suurusega väärtusi kaks võrdset. Seega ei ole diagramm A kindlasti koostatud samadest andmetest, millest ülejäänud.
Andmete töötlemisel võib kergesti juhtuda, et midagi läheb valesti. Sellepärast on alati kasulik oma töö tulemusele peale vaadata ja mõelda, kas seal on midagi, mis ilmselgelt ei klapi või ei sobi.

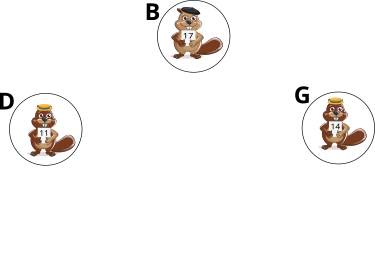
Kobras laadis Internetist oma arvutisse 10 pilti:

Nüüd tahab ta ekraanil näidata neist kolme, vastavalt järgmistele tingimustele:
| Vasakul | Keskel | Paremal | |
|---|---|---|---|
| Pildi kuju |  |
 |
 |
| Mütsi kuju |  |
 |
 |
| Arv pildil | Väiksem kui 16 | Suurem kui 11 | Täpselt 8 |
Mütsi juures on tähtis ainult selle kuju, mitte värv.
Millised pildid ilmuvad ekraanile?
(Kirjuta nende tähised tähestikulises järjekorras, näiteks ABC.)
[Tekstikast]
Õige vastus on: AGI.
Alustame kõigi piltide hulgast ja vaatame järjest kõiki tingimusi:
| Vasakul | Keskel | Paremal |
|---|---|---|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
See ülesanne on näide andmete filtreerimisest läbi mitme tingimuse. Me võime tingimuste tabeli iga veergu vaadata kui toru ja iga tingimust kui filtrit selles torus, mis laseb edasi liikuda ainult tingimusele vastavatel piltidel ja peab kõik mittevastavad pildid kinni. Selliseid mitmest sammust koosnevaid "torusid" nimetatakse arvutiteaduses konveieriteks (ingl pipeline) ja neid kasutatakse sageli, et lihtsamatest filtritest keerulisemaid kokku panna.
Tegelikult on konveierid kasutusel ka mujal kui andmete filtreerimisel. Tihti koostatakse konveiereid ka elementidest, mis igaüks muudavad andmeid mingil kindlal viisil. Näiteks võime koostada konveieri, mis saab ühe kooli õpilaste andmed ja mille esimene samm jätab iga õpilase andmetest alles ainult sünnikuupäeva, teine samm asendab iga kuupäeva sellele vastava nädalapäevaga ja kolmas loeb iga nädalapäeva kohta kokku selle esinemiste arvu. Nii saame konveieri lõpust kätte statistika, mis ütleb, kui palju igal nädalapäeval sündinud lapsi selles koolis õpib.
Kuigi konveieri iga element tegi ühe lihtsa operatsiooni, saime nende õigesti kombineerimisega lahendada päris keerulise ülesande. Selles peitubki konveierite kasulikkus.

Kolamid on dekoratiivsed mustrid, mida saab põrandale joonistada näiteks kriidiga. Kolami joonistamiseks märgitakse kõigepealt ära mõned punktid ja seejärel tõmmatakse nende ümber jooned. Iga joont alustatakse ja lõpetatakse samas punktis, joonistamise ajal kriiti üles ei tõsteta. Jooned võivad üksteisega ristuda, kuid neil ei tohi olla teravaid nurki.
Sellise kaare joonistamine on lubatud:

Selline nurk on terav ning selle joonistamine on keelatud:

Siin on üks kolami joonistamise näide:
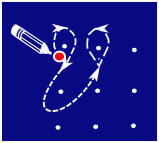
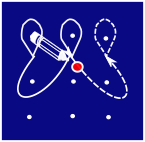
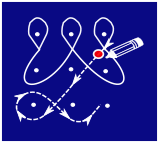
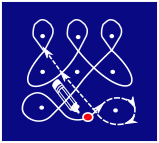

Millist alltoodutest ei saa sel viisil joonistada?
[Raadionupud]
A. 
B. 
C. 
D. 
Õige vastus on: C.
Variantide A, B ja D disain on pidev. Nende joonistamisel võime alustada kujutise suvalisest punktist ja järgida kõveraid, kuni jõuame alguspunkti tagasi.
Variant C aga koosneb kahest kolami tingimustele vastavast joonest:


Seda kujundit saaks joonistada ka ühe joonega, aga siis peaks vähemalt kahes kohas joonistama terava nurga, mis pole kolami reeglitega lubatud.
Kolamid on keerulised mustrid, mida leidub India linnades ja külades. Kuidas neid mustreid mäletatakse ja joonistatakse? Üks teooria on, et neid luuakse lihtsate reeglite järgi, mida antakse edasi põlvest põlve.
Reeglikogumite järgi neile vastavate tekstide genereerimist uuritakse arvutiteaduses formaalsete keelte teoorias. Kuigi genereerivad grammatikad mõeldi algselt välja tekstide (ühemõõtmeliste märgijadade) kirjeldamiseks, on hiljem seda ideed laiendatud ka mitmemõõtmelistele objektidele, sealhulgas ka graafilistele kujunditele. Selliseid meetodeid kasutatakse sageli ka generatiivses kunstis (ingl generative art).

Vaatame 6x5 ruudust koosnevat pilti, mille osad ruudud on punased, osad valged:
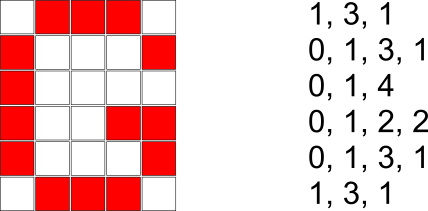
Selle pildi saab teisendada arvujadaks, lugedes iga rea puhul üle, mitu järjestikust ruutu on valged, seejärel mitu järjestikust ruutu on punased, siis mitu järjestikust ruutu on valged jne, kuni jõuame rea lõppu. Pane tähele, et kui rida algab punase ruuduga, siis on selle rea alguses olevate valgete ruutude arv 0.
Lõpuks ühendame kõigi pildiridade kõik arvud ühte jadasse. Eeltoodud näites oleks tulemuseks selline jada: 1, 3, 1, 0, 1, 3, 1, 0, 1, 4, 0, 1, 2, 2, 0, 1, 3, 1, 1, 3, 1.
Milline on allolevat pilti kirjeldav arvujada?

[Raadionupud]
A. 0, 1, 3, 4, 1, 1, 3, 1, 0, 2, 2, 1, 0, 1, 3, 1, 2, 2, 1
B. 1, 3, 1, 4, 1, 1, 4, 0, 1, 3, 1, 0, 1, 3, 1, 1, 3, 1
C. 1, 3, 1, 0, 1, 4, 1, 4, 0, 1, 3, 1, 0, 1, 3, 1, 1, 3, 1
D. 1, 3, 1, 4, 1, 1, 4, 1, 3, 1, 1, 3, 1, 1, 3, 1
Õige vastus on: B.
Vastuse leidmiseks on vaja vähemalt neli pildirida arvudeks teisendada ja seejärel ühendada:
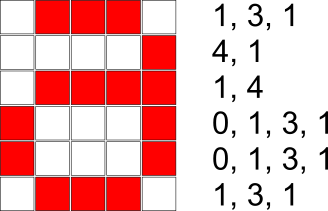
Tulemuseks on jada 1, 3, 1, 4, 1, 1, 4, 0, 1, 3, 1, 0, 1, 3, 1, 1, 3, 1, mis vastab variandile B.
Ülejäänud kolm vastust esindavad teisi pilte, kuna iga pildi esitus on üheselt määratud. Teisisõnu: erinevad esitused vastavad alati erinevatele piltidele.
Piltide salvestamiseks või edastamiseks elektroonikaseadmete vahel on vaja need arvudeks teisendada. Selleks on palju viise ja siin on toodud neist üks. Kasutades ühte arvu sama värvi ruutude jada esitamiseks, tihendab see meetod andmeid ehk vähendab andmete hulka ja see on informaatikas oluline. Seda meetodit saab täiustada mitmel viisil, näiteks lubades arvul viidata rohkem kui ühte rida hõlmavale ruutude jadale.
Andmete esitamise viiside leidmine on olnud väljakutse alates juba esimestest elektroonilistest seadmetest, sest sellega seotud valikud võivad mõjutada teabe töötlemiseks või saatmiseks ja vastuvõtmiseks kuluvat aega. Praegu on see probleem endiselt aktuaalne, eriti internetis: uute viiside loomine piltide, videote ja muude meediumifailide kodeerimiseks võib meie veebikasutamist kiirendada.
Selles ülesandes kirjeldatud meetodit kasutasid vanad faksiaparaadid dokumentide sisu edastamiseks.
Copyright © 2022 Bebras – International Challenge on Informatics and Computational Thinking.
Licensed under Creative Commons Attribution-ShareAlike 4.0 International License.
Flag icons by GoSquared.