


Каждый год в день своего рождения Саша ставит на праздничный торт свечи и таким образом указывает свой новый возраст. Он использует свечи трёх цветов: оранжевые, красные и синие. Все свечи в форме «0» — оранжевые, все свечи в форме «1» — красные и т.д. (см. таблицу).
| Цифра | Цвет |
|---|---|
| 0 | Оранжевый |
| 1 | Красный |
| 2 | Синий |
| 3 | Оранжевый |
| 4 | Красный |
| 5 | Синий |
| 6 | Оранжевый |
| 7 | Красный |
| 8 | Синий |
| 9 | Оранжевый |
Сегодня Саше исполнилось 11 лет, поэтому обе свечи на торте были одного и того же цвета. Ему придётся ждать ещё три года, пока не исполнится 14 лет, чтобы обе свечи на торте вновь стали одного и того же цвета. Затем Саше придётся ждать ещё три года, пока не исполнится 17 лет, а потом ещё пять лет, пока не исполнится 22.
Если бы Саша использовал эту систему с сегодняшнего дня до своего 99-летнего дня рождения, то какое наибольшее количество лет ему пришлось бы ждать между двумя днями рождения, чтобы для обозначения его возраста были использованы две свечи одного и того же цвета?
[Raadionupud]
A. 5 лет
B. 6 лет
C. 7 лет
D. 8 лет
Правильный ответ: A (5 лет).
Пусть XY — текущий возраст человека, где X и Y — это две цифры в промежутке от 0 до 9, а на основании предложенной в задании таблицы X и Y ещё являются одного и того же цвета. Предположим, что Y — это одна из цифр 0, 1, 2, 3, 4, 5 или 6. В этом случае нужно ждать три года до возраста X(Y + 3), чтобы увидеть на торте две свечи одного и того же цвета.
Далее рассмотрим отдельно случаи, когда Y равно 7, 8 или 9:
Поэтому наибольшее количество лет ожидания будет равно 5 годам, а не 6 или более лет.
В этом задании последовательность двузначных чисел представлена в виде последовательности пары цветов. n-ный элемент этой абстрактной последовательности представлен цветами двух свечей, которые используются для представления числа n. Довольно часто в информатике говорится о правилах формирования последовательности и приходится моделировать последовательность до тех пор, пока не будут выполнены определенные условия.
Аспекты вычислительного мышления, иллюстрируемые в этом задании, включают алгоритмы, представление и распознавание паттернов.
Алгоритмы: задание является примером анализа алгоритма. В задании представлен алгоритм, генерирующий последовательность пары цветов, то есть цветов свечей, используемых для представления каждого двузначного числа. Поиск ответа путем моделирования последовательности занял бы слишком много времени, поэтому вместо этого мы должны проанализировать свойства алгоритма и при необходимости использовать моделирование коротких отрезков последовательности.
Представление: в задании числа представлены в виде пары цветов (мы говорим, что числа сопоставляются с парами цветов). В задании мы должны постоянно применять это правило к разным числам, чтобы определить числа, представленные парой свечей одного и того же цвета.
Распознавание паттернов: в некоторой степени задание также является примером распознавания паттернов. В задании дается паттерн (шаблон), который в данном случае представляет собой последовательность пар цветов свечей, где цвета представлены с помощью простого алгоритма.

Во время отдыха на острове Таити Марина и Вероника купили себе бусинки и сделали из них ожерелья. Получившиеся ожерелья выглядят следующим образом:
Марина:

Вероника:

В какой-то момент девочки решили обменяться бусинками из своих ожерелий, выполнив следующие шаги:
Как будут выглядеть ожерелья Марины и Вероники после выполнения этих шагов?
[Raadionupud]
A. 
B. 
C. 
D. 
Правильный ответ: D.
Чтобы понять, почему вариант D правильный, давайте проследим каждый шаг отдельно. Начнем с первоначального состояния двух ожерелий:
Марина:

Вероника:

Выполняя описанные выше шаги, девочки по очереди снимают по одной бусинке с правого конца своего ожерелья; Марина начинает первой. В приведённом ниже объяснении термин «итерация» обозначает однократное прохождение шагов 1–3. Ниже также приведён рисунок, показывающий полученный после каждой итерации результат. На рисунке первая пара цветных линий обозначает первоначальное состояние ожерелий, последующие пары цветных линий обозначают состояния ожерелий после каждой итерации.
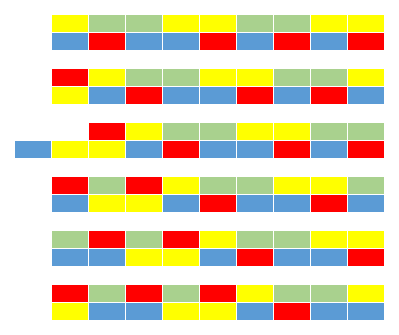
Итерация 1: Поскольку первая бусинка на правых концах обоих ожерелий жёлтая или красная, её снимают и добавляют к левому концу ожерелья подруги. Таким образом, каждая девочка отдала по одной бусинке.
Итерация 2: Поскольку на правом конце ожерелья Марины есть жёлтая бусинка, она добавляет её к левому концу ожерелья Вероники. У Вероники есть синяя бусинка, поэтому девочка её не отдаёт, а просто добавляет к левому концу своего ожерелья. Получается, что Марина уже отдала две бусинки, а Вероника одну.
Итерация 3: Следующая бусинка Марины зелёная, поэтому она добавляет её к левому концу своего ожерелья. Следующая бусинка Вероники красная, она добавляет её к левому концу ожерелья Марины. Каждая отдала по две бусинки.
Итерация 4: Следующая бусинка Марины зелёная, она добавляет её к левому концу своего ожерелья. Следующая бусинка Вероники синяя, поэтому она добавляет к левому концу своего ожерелья. Каждая девочка отдала по две бусинки.
Итерация 5: Следующая бусинка в ожерельях девочек жёлтая или красная, поэтому девочки меняются бусинками и добавляют их к левому концу своего ожерелья. Теперь каждая отдала по три бусинки.
Так как каждая девочка отдала по три бусинки, обмен прекращается и получившиеся ожерелья выглядят как на рисунке ниже, т.е. вариант ответа D.
Марина:

Вероника:

Вариант А не может быть правильным, потому что каждая из девочек должна была отказаться от трёх бусинок, а в этом варианте в ожерелье Марины четыре красных бусинки, а в ожерелье Вероники четыре жёлтых бусинки, которых у них раньше не было.
Вариант B не может быть правильным, потому что у каждой девочки в ожерелье только две бусинки нового цвета.
Вариант С тоже неправильный. Хотя количество бусинок разных цветов в ожерелье правильное, расположены они в неправильном порядке.
С помощью этого задания мы можем объяснить понятие очереди в информатике. Очередь — это список, элементы которого добавляются только с одного конца и удаляются только с другого конца. При хранении данных такой метод называется структурой FIFO (англ first in, first out). Это полезная структура данных, поскольку она сохраняет порядок добавления элементов.
Ожерелья Марины и Вероники можно считать упорядоченными. Хотя мы не выясняли, как бусинки были нанизаны на ожерелье, правила объясняют, что один конкретный конец предназначен только для добавления новых бусинок, а другой конец — только для их удаления.

Боря составляет "слова", используя нижеприведённый рисунок. Он всегда начинает с кружка с надписью "Начало" и следует стрелкам до тех пор, пока не доберётся до кружка с надписью "Конец". Боря записывает каждую букву, которую проходит на своём пути.
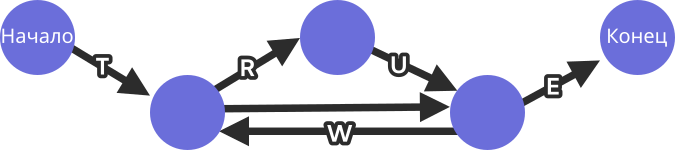
Из вышеприведённого рисунка видно, что, действуя таким образом, он может составить такие слова как "TRUE" или "TWWWE".
Сколько различных 8-буквенных слов Боря может составить таким образом?
[Täisarv]
Правильный ответ: 9.
Прежде всего отметим, что всегда все слова должны начинаться с буквы "Т" и заканчиваться буквой "Е". Итак, между этими двумя буквами ищем 6-буквенные последовательности, состоящие из букв "R", "U" и "W".
Мы можем заметить, что Боря может двигаться от конца стрелки "Т" к началу стрелки "Е", записывая либо пару букв "RU", либо вообще ничего не записая, но обратно он может вернуться только через букву "W". Чтобы не упустить ни одной возможности, системно просмотрим возможности комбинирования этих способов передвижения:
Таким образом, Боря может получить 1+5+3=9 различных слов.
Перебор всех возможностей — это то действие, в котором компьютер действительно хорош. В данном случае мы записывали все подходящие слова, помня при этом, что составленные слова не могут повторяться. В этом задании приведён пример алгоритмической "машины", генерирующей последовательности букв с заданными ограничениями. Такие системы иногда используются для генерации паролей для участников викторины Бобр или для изготовления номерных знаков автомобилей, или вообще в тех случаях, когда необходимы уникальные последовательности символов, которые должны следовать заранее определённому формату. При этом часто бывает необходимо проверить, можно ли составить достаточное количество различных слов по выбранному паттерну.

На рисунке изображены мельницы и соединяющие их с хранилищем муки дорожки. Каждый вечер на мельницах перемалывается мука, которая затем оставляется в мешках перед мельницами. Бобр Вилли должен собрать все мешки и перенести их в хранилище до заката. Вилли может одновременно нести несколько мешков, если их общий вес не превышает 15 кг. На рисунке также указано время, которое требуется Вилли для прохождения каждого участка дорожки.
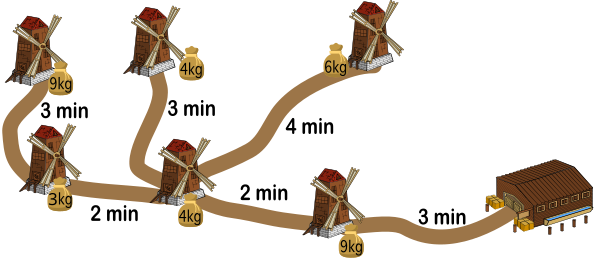
Вилли начинает с хранилища и хочет как можно быстрее перенести все мешки в хранилище.
Какое наименьшее количество минут ему понадобится для выполнения этого задания?
[Raadionupud]
A. 31 минута
B. 44 минуты
C. 50 минут
D. 54 минуты
Правильный ответ: C (50 минут).
Общий вес муки во всех мешках 35 кг. Поскольку за один заход Вилли может перенести максимум 15 кг, то он должен сделать не менее трёх заходов, чтобы перенести все мешки в хранилище. Чтобы минимизировать расходы своего времени, бобр должен за один заход забрать мешки от как можно большего количества мельниц, находящихся в непосредственной близости друг от друга.
Например, вместе с 9-килограммовым мешком, который находится около верхней левой мельницы, Вилли может забрать и 3-килограммовый мешок от соседней мельницы (общий вес 12 кг). Все остальные мешки весят более 3 кг, поэтому Вилли не может забрать больше мешков за этот заход. Этот путь займёт 3+2+2+3+3+2+2+3=20 минут.
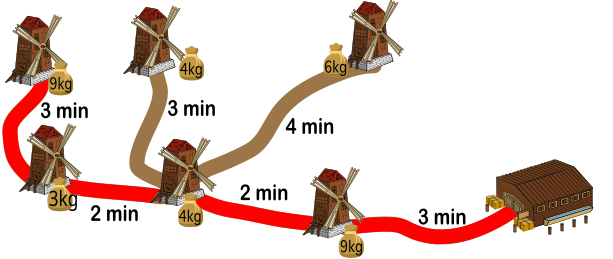
Во второй заход бобр может забрать три самых дальних из четырёх оставшихся мешков: 6-килограммовый мешок от расположенной наверху правой мельницы и два 4-килограммовых мешка от двух расположенных по середине мельниц (общий вес 14 кг). Этот путь займёт 3+2+4+4+3+3+2+3=24 минуты.
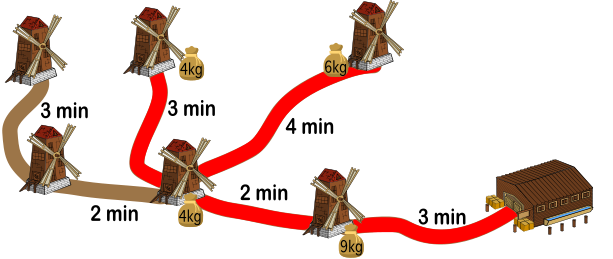
Во время третьего захода Вилли перенесёт в хранилище оставшийся 9-килограммовый мешок от ближайшей мельницы и ему потребуется 3+3=6 минут.
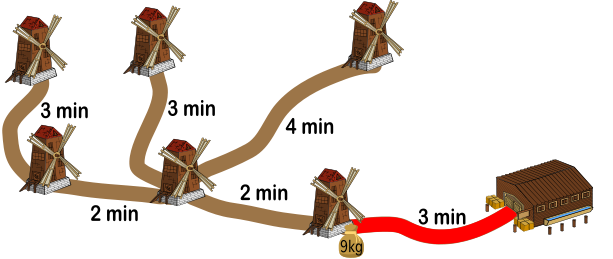
Таким образом, чтобы перенести все мешки в хранилище, потребуется в общей сложности 20+24+6=50 минут.
Порядок вышеперечисленных заходов может быть изменён, единственное, что важно, это разумная группировка мешков.
Вариант А точно не может быть правильным, потому что доставка 9-килограммового мешка от расположенной наверху левой мельницы уже заняла бы 20 минут (независимо от того, забрал бы Вилли 3-килограммовый мешок от соседней мельницы или нет). Оставшихся 10 минут хватило бы только на то, чтобы добраться до второй мельницу и вернуться. В этом варианте Вилли не успел бы перенести два мешка с расположенных наверху мельниц.
Вариант B тоже не может быть правильным, потому что 44 минуты — это как раз то общее время, которое потребуется для первого и второго захода, а 9-килограммовый мешок муки от ближайшей мельницы нельзя добавить ни к одному из этих заходов.
Вариант D не является правильным ответом, так как мы уже знаем, что есть решение, требующее меньшего времени.
В информатике задачами оптимизации называют такие задачи, целью которых является поиск наилучшего решения среди всех возможных решений. Обычно это связано с нахождением максимального или минимального значения некоторой функции. Например, в этом задании нас просят найти минимальное общее время. Решение задач с помощью компьютеров также часто связано с оптимизацией. Мы часто хотим, чтобы компьютер мог выполнить свою задачу в кратчайшие сроки или с минимальным использованием какого-либо другого ресурса, например, памяти.
В этом задании мы можем найти наилучшее решение, перепробовав все возможные маршруты самостоятельно или с помощью компьютера и выбрав среди них вариант с наименьшим временем. Этот подход известен как метод грубой силы (англ brute force) или полного перебора (англ exhaustive search). Этот подход подходит для небольших задач (в данном случае количество мельниц, с которых надо забрать муку, и дорожек невелико). Если проблема большая, метод грубой силы работает очень медленно, потому что возможных вариантов может быть слишком много. Поэтому существуют другие подходы, позволяющие более эффективно находить решения многих проблем. Например, жадные алгоритмы (англ greedy algorithm) или динамическое программирование (англ dynamic programming).
Для точного решения многих задач неизвестно более эффективного метода, чем просто детальный просмотр. Если надо решить такое задание для большого объёма данных, то часто приходится довольствоваться приближёнными методами, которые не обязательно находят наилучшее решение, но часто дают достаточно хороший результат для использования на практике.

Аня и Яна являются хозяйками ресторана. При помощи лампы, передающей сигналы в форме листика или цветка, Аня посылает Яне заказы на еду. Каждое блюдо в меню ресторана имеет уникальный код, который формируется этими двумя формами. Аня включает и выключает свет в нужной форме в порядке, соответствующем коду заказа, а Яна готовит соответствующую еду.
С самого начала работы ресторана Аня и Яна договорились о следующих кодах для двух блюд в меню своего ресторана:
| Блюдо | Код |
|---|---|
| Бургер |   |
| Жареный рис |    |
Проблема заключалась в том, что Яна начинала готовить еду сразу, как только понимала, что полученный код соответствовал какому-то блюду из меню. Когда Аня для заказа жареного риса использовала код, где в начале необходимо было дважды передать сигнал в форме листика, Яна вместо риса начинала уже готовить бургер. Таким образом, жареный рис никогда не готовился.
Чтобы решить эту проблему, они решили изменить коды. Теперь обновлённое меню с новыми кодами выглядит следующим образом:
| Блюдо | Код |
|---|---|
| Бургер |   |
| Жареный рис |     |
| Бутерброд |   |
| Пицца |    |
| Пирожное |    |
Девочки решили добавить в меню ещё и картофель фри.
Какой из следующих кодов можно было бы использовать для заказа картофеля фри?
[Raadionupud]
A. 


B. 


C. 


D. 



E. 



Правильный ответ: A.
Яна начнёт готовить не то блюдо, если его полный код совпадёт с первой частью какого-то другого кода. Поэтому ни у одного из блюд начало кода не должно содержать полный код любого другого блюда.
Таким образом, вариант B не является правильным ответом, потому что полный код бургера идентичен началу варианта B.
| Блюдо | Код |
|---|---|
| Бургер |   |
| Вариант B |    |
То же самое относится к пирожному и варианту D, а также к пицце и варианту E.
| Блюдо | Код |
|---|---|
| Пирожное |    |
| Вариант D |     |
| Блюдо | Код |
|---|---|
| Пицца |    |
| Вариант E |     |
Вариант C также не является подходящим решением, потому что полный код варианта C идентичен началу кода жареного риса.
| Блюдо | Код |
|---|---|
| Жареный рис |     |
| Вариант C |    |
Вариант А является правильным ответом, потому что его полный код не совпадает с началом любого другого кода, а полный код ни одного другого блюда не идентичен началу кода варианта А.
Ане и Яне нужно правило кодирования, при котором ни один из полных кодов не является началом какого-либо другого кода. Коды с этим свойством называются префиксными кодами (англ prefix code). В информатике их используют во многих местах для представления данных.
Простой способ получить префиксный код — это дать всем кодируемым объектам разные коды одинаковой длины. Например, для представления английских текстов часто используется ASCII-код, где каждой букве соответствует 7-битный код (7-значный номер, состоящий из 0 и 1). Однако такой простой метод часто оказывается малоэффективным.
Более разумное решение — это давать часто встречающимся буквам более короткие коды. За счёт этого слова занимают меньше места при кодировании. Буквы можно кодировать последовательностями из битов, и эти последовательности могут быть разной длины. Но всё это возможно только при условии, что не существует последовательности битов, которая кодировала бы букву и при этом была бы идентичной началу последовательности битов, которая кодирует другую букву. Например, если «а» является наиболее часто встречающейся буквой, за которой следует «е» и намного реже «d», то мы можем использовать 0 для кодирования «а», 10 для «е» и 110 для «d». Если мы закодируем таким образом слово «aed», то получим 010110. Поскольку это префиксный код, мы можем однозначно восстановить текст из закодированной последовательности битов, и 010110 всегда будет декодироваться как «aed». Если бы мы закодировали то же слово с помощью ASCII-кода, то оно заняло бы 3x7=21 бит вместо 6 бит. Такую идею используют, например, некоторые программы сжатия данных.

У Ани на работе есть 3 коллеги, использующие один и тот же сетевой принтер, который стоит рядом с их рабочими столами. Когда один из коллег отправляет документ на печать, то принтер запускается и распечатывает весь документ. Если во время распечатывания этого документа на печать отправляется какой-нибудь другой документ, то принтер сначала завершает распечатывать текущий документ и только затем приступает к распечатыванию нового документа.

Сегодня в офисе напряжённый день, и необходимо распечатать много документов разных объёмов. В следующих таблицах для каждого коллеги указано время отправки каждого документа на печать и время, которое необходимо для распечатывания этого документа. Если печать документа начинается в 10:00 и длится 2 минуты, то печать завершится в 10:02. Между двумя последовательными распечатываниями документов нет времени ожидания, и принтер может начать распечатывать следующей документ сразу в 10:02.
Коллега Боря:
| Номер работы | Время отправки | Продолжительность |
|---|---|---|
| 11 | 10:00 | 2 мин |
| 12 | 10:03 | 1 мин |
| 13 | 10:10 | 5 мин |
Коллега Елена:
| Номер работы | Время отправки | Продолжительность |
|---|---|---|
| 21 | 10:01 | 1 мин |
| 22 | 10:04 | 3 мин |
| 23 | 10:12 | 1 мин |
Коллега Коля:
| Номер работы | Время отправки | Продолжительность |
|---|---|---|
| 31 | 10:05 | 3 мин |
| 32 | 10:08 | 5 мин |
| 33 | 10:13 | 1 мин |
В каком порядке распечатываются документы и во сколько принтер завершит распечатывать все документы?
[Raadionupud]
A. 11 12 13 21 22 23 31 32 33, время завершения распечатывания 10:22
B. 11 21 12 22 31 32 13 23 33, время завершения распечатывания 10:14
C. 11 12 13 21 22 23 31 32 33, время завершения распечатывания 10:14
D. 11 21 12 22 31 32 13 23 33, время завершения распечатывания 10:22
Правильный ответ: D.
В нижеприведённой таблице показана последовательность распечатывания документов и время для распечатывания каждого документа:
| Номер работы | Время отправки | Время начала | Продолжительность | Время окончания |
|---|---|---|---|---|
| Работа 11 | 10:00 | 10:00 | 2 мин | 10:02 |
| Работа 21 | 10:01 | 10:02 | 1 мин | 10:03 |
| Работа 12 | 10:03 | 10:03 | 1 мин | 10:04 |
| Работа 22 | 10:04 | 10:04 | 3 мин | 10:07 |
| Работа 31 | 10:05 | 10:07 | 3 мин | 10:10 |
| Работа 32 | 10:08 | 10:10 | 5 мин | 10:15 |
| Работа 13 | 10:10 | 10:15 | 5 мин | 10:20 |
| Работа 23 | 10:12 | 10:20 | 1 мин | 10:21 |
| Работа 33 | 10:13 | 10:21 | 1 мин | 10:22 |
Для управления документами принтер использует структуру данных, которая называется очередь (англ queue). Очередь — это абстрактная структура данных, в которую данные добавляются с одного конца и удаляются с другого конца. Из элементов в очереди можно просмотреть только тот элемент, который находится в начале очереди и который будет удален из неё следующим.
С помощью очереди можно выполнить следующие действия:
Эти действия аналогичны, например, очереди в магазине. Новые покупатели становятся в конец очереди и их обслуживают только тогда, когда подошла их очередь. Вот почему также говорят, что очередь является структурой типа FIFO (англ first in, first out). В информатике также используется очередь, когда необходимо обрабатывать информацию в том порядке, в котором она была создана или получена, например, при представлении сообщений в системе чата или при передаче данных по компьютерной сети.

Маленький Бобр планирует вечеринку по случаю дня рождения. Он составляет список заданий, которые необходимо выполнить перед вечеринкой.
| Задание | Предыдущее задание |
|---|---|
 Уточнение количества гостей Уточнение количества гостей |
 |
 Закупка продуктов Закупка продуктов |
  |
 Выбор даты Выбор даты |
- |
 Расчёт расходов Расчёт расходов |
   |
 Выбор места проведения Выбор места проведения |
 |
Он понимает, что ему нужно выполнить несколько других заданий, прежде чем он сможет начать какие-либо другие задания. Например, прежде чем он узнает количество гостей, ему нужно выбрать дату вечеринки.
Какой из следующих вариантов является правильным порядком выполнения заданий?
[Raadionupud]
A.  →
→  →
→  →
→  →
→ 
B.  →
→  →
→  →
→  →
→ 
C.  →
→  →
→  →
→  →
→ 
D.  →
→  →
→  →
→  →
→ 
Правильный ответ: C.
Если мы разместим обозначающие задания кружки на рисунке в порядке, указанном в варианте С, и проведём стрелки от каждого предыдущего задания к следующему, то мы увидим, что все стрелки указывают слева направо. Это показывает, что в варианте C указан правильный порядок.
Варианты A и B не могут быть правильными, потому что бобр должен выбрать дату, прежде чем он узнает, сколько гостей придёт. Вариант D также невозможен, так как перед расчётом затрат следует уточнить, сколько гостей придёт.
Такое упорядочивание действий называется топологической сортировкой (англ topological sorting). Для компьютера проще всего сортировать данные в числовом порядке. Однако, если подлежащие сортировке элементы не имеют числовых характеристик или если мы хотим отсортировать их на основе нечисловых характеристик, то мы должны определить положение каждого элемента относительно других элементов. Часто для представления последовательности мы можем использовать схему, подобную приведённой в объяснении ответа. В информатике такие схемы называются графами (англ graph).
Топологическая сортировка используется в повседневной жизни при планировании работы или заданий, но часто мы даже не задумываемся об этом. Простой пример — это одевание, когда мы сначала должны одеть нижнее бельё, а затем одежду, и сначала носки, а потом сапогами, но порядок одевания шапки и сапог не важен.

Учитель Маттеус решил организовать вечер кино для своих семи учеников. Для этого он использует школьный актовый зал, в котором стоит овальный стол.
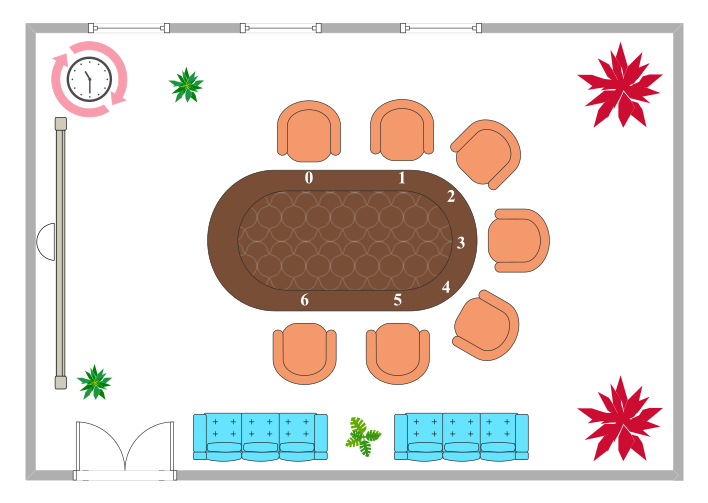
Учитель установил следующие правила распределения мест:
Правило дня рождения: каждый ученик сидит на стуле, номер которого равен сумме чисел, обозначающих день и месяц его рождения. Если сумма равна 7 или больше, то на номер стула указывает остаток, полученный при делении на 7. Например, Янис сидит на стуле под номером 1, потому что он родился 24.12, а 24+12=36 и при делении 36 на 7 остаток равен 1.
Правило перекрытия: если стул, предназначенный ученику в соответствии с правилом дня рождения, уже занят, то ученик должен сесть на следующий стул. Например, если стул 2 занят, то ученик садится на стул под номером 3; а если и стул 2, и стул 3 заняты, то ученик садится на стул под номером 4. Если стул под номером 6 занят, то ученик садится на стул под номером 0.
В таблице указаны дни рождения учеников в том порядке, в котором они заходили в зал:
| Имя | День рождения |
|---|---|
| Маша | 05.01 |
| Харри | 08.02 |
| Эмилия | 30.01 |
| Йоханна | 09.09 |
| Янис | 24.12 |
| Медея | 16.04 |
| Сара | 02.12 |
На какой стул сядет Сара?
[Raadionupud]
A. Стул под номером 0
B. Стул под номером 4
C. Стул под номером 2
D. Стул под номером 5
Правильный ответ: C (стул под номером 2).
Ученики сидят так, как показано на нижеприведённом рисунке:
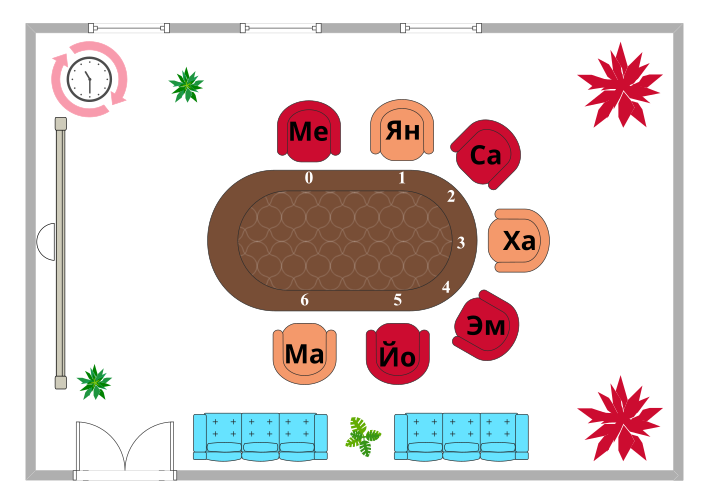
Оранжевый цвет стула указывает на то, что ученик не должен был использовать правило перекрытия и сразу сел на этот стул. Красный цвет стула указывает на то, что ученику пришлось подойти как минимум к одному следующему стулу, прежде чем он нашёл свободное место.
Для составления такого плана рассадки необходимо сначала вычислить суммы чисел, представляющих день и месяц рождения ученика, а затем вычислить остатки этих сумм при делении на 7.
| Имя | День рождения | Сумма | Остаток |
|---|---|---|---|
| Маша | 05.01 | 6 | 6 |
| Харри | 08.02 | 10 | 3 |
| Эмилия | 30.01 | 31 | 3 |
| Йоханна | 09.09 | 18 | 4 |
| Янис | 24.12 | 36 | 1 |
| Медея | 16.04 | 20 | 6 |
| Сара | 02.12 | 14 | 0 |
Таблица показывает, что как Маша, так Медея должны были бы сидеть на стуле под номером 6, но только одна из них может там сидеть. Маша села первой. Значит, Медея должна сесть на другой стул.
Кто где сидит мы узнаем, если рассмотрим порядок, в котором ученики заходили в зал, и для каждого из учеников найдём первое свободное место, используя указанные в таблице номера стульев и двигаясь вдоль стола по направлению движения часовой стрелки.
В информатике часто необходимо решать проблемы равномерного распределения данных. Одним из примеров является поиск подходящего места на диске компьютера для хранения файла. Этот подход также эффективен для последующего поиска сохранённых на диске файлов. Такой подход называется хешированием (англ hashing).
Это задание также является примером модульной арифметики (англ modular arithmetic), где вместо ответа, полученного в результате обычных операций сложения или умножения, используется остаток, возникающий при делении ответа на некоторое число (т.н. модуль). В этом задание модуль равен 7. Известными примерами модульной арифметики являются 12- и 24-часовые форматы времени. Например, если сейчас 10 часов утра, то в случае 24-часового формат через 4 часа мы скажем что уже 10+4=14 часов, а в случае 12-часовом формате системе мы скажем, что это будет 2 часа дня. Причина этого в том, что деление 14 на 12 даёт остаток 2. Вычисляя по модулю 7, мы можем найти день недели, например, через 10 или 12 дней.


Бобру Диане в качестве подарка прислали нарисованное сердечко. Скорее всего, это сделал кто-то из её четырёх лучших друзей. Каждый из друзей сказал по одному предложению:
Однако у этой четвёрки есть странная привычка — правду всегда говорит только один из них.
Кто отправил сердечко?
[Raadionupud]
A. Ваня
B. Толя
C. Коля
D. Роберт
Правильный ответ: D (Роберт).
Поскольку мы знаем, что только одно из четырёх утверждений верно, то только Роберт мог отправить сердечко.
Это задание представляет собой логическую задачу. Сначала мы используем декомпозицию, т.е. мы делим сложную проблему на более мелкие, легко анализируемые части. Например, мы можем рассматривать как подзадачу задачу о том, какое из данных утверждений верно. Затем нам нужна абстракция, чтобы отбросить ненужную информацию и сосредоточиться на важных фактах. Например, мы предполагаем, что какое-то утверждение верно, рассматриваем относящуюся к нему информацию и игнорируем всё остальное. Таким образом мы за один раз сосредотачиваемся на одном утверждении, далее используем связанную с этим утверждением информацию и смотрим, сможем ли мы найти противоречия в других приведённых утверждениях.
Четверо друзей высказывают простые утверждения. Все эти утверждения (или заявления) могут быть только истинными или ложными. В 1847 году Джордж Буль сформулировал способы того, как учитывать истинность таких простых утверждений. Он использовал логику высказываний (англ propositional calculus). Этот набор правил высказываний говорит нам, как сконструировать новые истинные утверждения из существующих истинных утверждений без учёта их фактического значения. Компьютеры также работают на основе этой логики: наименьшая единица информации, т.е. бит, похожа на утверждение поскольку может нести только два разных значения (истина или ложь, соответственно). Логика высказываний является основой огромного успеха цифровых вычислений и информатики.

Для школьного проекта Вера сделала коллаж, наложив полоски бумаги друг на друга.
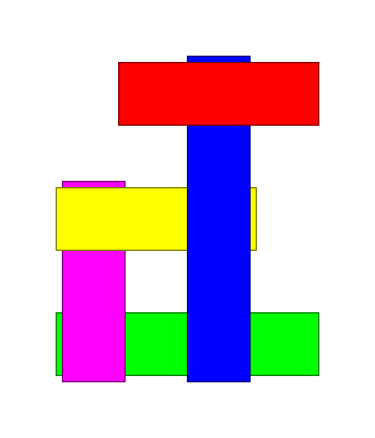
Лена, младшая сестра Веры, хотела сделать такой же коллаж. Но когда Лена взяла в руки коллаж сестры, полоски бумаги упали и на месте осталась только зелёная полоска. Лена должна положить полоски бумаги друг на друга точно так, как они были в начале, чтобы Вера не узнала о происшествии. Помоги Лене!
В каком порядке Лена должна положить полоски обратно?
[Raadionupud]
A. Фиолетовый, жёлтый, синий, красный
B. Красный, синий, жёлтый, фиолетовый
C. Жёлтый, фиолетовый, синий, красный
D. Фиолетовый, синий, жёлтый, красный
Правильный ответ: A (фиолетовый, жёлтый, синий, красный).


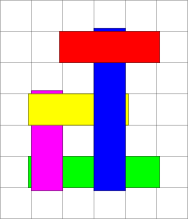
В компьютерной графике часто используется подход рисования изображений слоями. В этом случае нарисованные позже, на «верхних» слоях, фигуры частично или полностью стирают нарисованных ранее, на «нижних» слоях, фигуры. С помощью последовательности рисования фигур можно на экране создавать пространственные эффекты, когда кажется, что одни объекты находятся позади других.
Действует и обратная логика. В этом задании нужно было понять, какие из полосок были сверху, а какие снизу в коллаже. Аналогичный подход действует и в случае самоуправляемых автомобилей, когда на основе двухмерных видеоизображений необходимо решить, какие объекты в окружающем пространстве находятся ближе, а какие дальше. Автомобили также должны понимать, в каком направлении и с какой скоростью двигаются находящиеся вокруг них другие объекты. Область информатики, занимающаяся этими вопросами, называется компьютерным зрением (англ computer vision).

Бобр Марк ищет номер телефона своего друга на очень длинной интернет-странице. Марк не уверен, как точно пишется имя друга, поэтому использует для поиска специальные символы:
| Символ | Значение |
|---|---|
| ? | точно одна неизвестная буква |
| & | точно две неизвестные буквы подряд |
| % | любое количество неизвестных букв до конца имени |
Например, поисковый запрос «Ma%» может выдать имена Maрия, Maрк и т.д.
Какие из следующих имён выдаст поисковый запрос «S?rah B&cht%»?
(Отметь все правильные ответы.)
[Märkeruudud]
A. Sarah Birchtree
B. Sara Benchton
C. Sarah Bilchman
D. Sirah Beachtram
Правильный ответ: A, D.
Вариант A правильный, потому что имя «Sarah Birchtree» соответствует поисковому запросу «S?rah B&cht%»:
Вариант B не может быть правильным, потому что в имени «Sara» отсутствует буква «h».
Вариант C не может быть правильным, потому что в фамилии «Bilchman» вместо «cht» имеется «chm».
Вариант D правильный, потому что буквы имени и фамилии соответствуют используемому запросу: «S» и «S», «i» и «?», «rah» и «rah», пробел и пробел, «B» и «B», «ea» и «&», «cht» и «cht», а также «ram» и «%».
Многие информационные системы позволяют использовать для поиска информации так называемые символы подстановки (англ wildcard) или символы-джокеры. Примером их использования были специальные символы, которые были описаны в этом задании. Также во многих командах Windows, MacOS и Linux для одновременного именования нескольких файлов можно использовать «?», что означает «только один неизвестный символ», и «*», что означает «любое количество неизвестных символов».
Другой пример: многие программы обработки текста позволяют использовать так называемые регулярные выражения (англ regular expression). Эти выражения позволяют описать шаблоны, которые используются для поиска или замены текста.
Такие инструменты позволяют сэкономить время, потому что команда может быть одновременно применена ко многим файлам или словам. Без них команду пришлось бы давать отдельно для каждого файла или каждого возможного слова.

У бобра Максима в электронной таблице есть данные и формулы.

Теперь на основании вычисленных по формулам значений (в строке 3) он строит диаграммы.
Какую из приведенных ниже диаграмм Максим никогда не получит на основании этих данных?
[Raadionupud]
A. 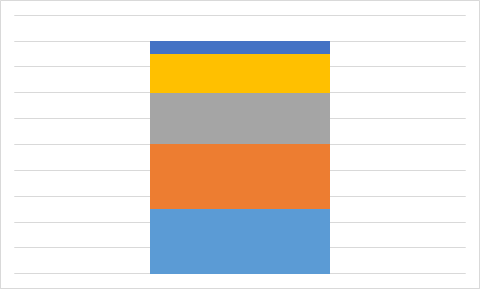
B. 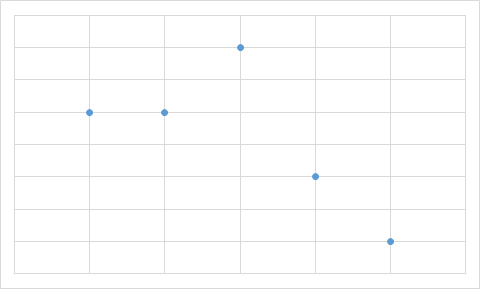
C. 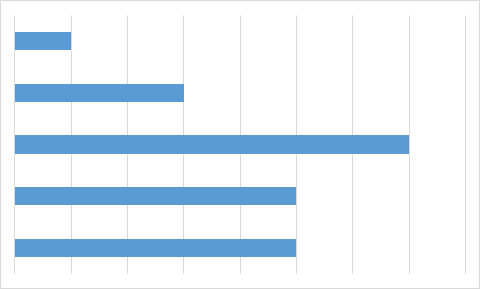
D. 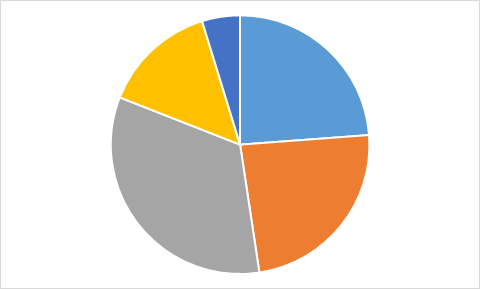
Правильный ответ: A.
Чтобы найти ответ, не нужно даже вычислять значения всех ячеек с формулами. Достаточно заметить, что на трёх диаграммах только одно значение является максимальным, а два следующих (по величине) значения — одинаковы. Однако на диаграмме А есть именно два равных максимальных значения. Поэтому диаграмма А определённо не составлена по тем же данным, что используются в остальных диаграммах.
При обработке данных может случиться так, что что-то случайно пойдёт не так. Именно поэтому всегда полезно посмотреть на результат своей работы и подумать, если там что-то такое, что явно не сходится или не подходит.

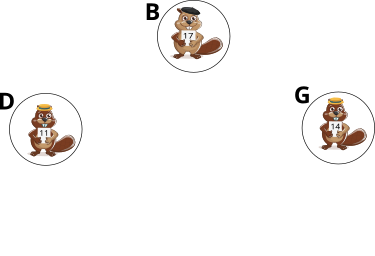
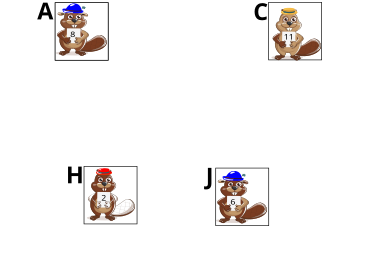
Бобр скачал из Интернета 10 фотографий:

Теперь он хочет вывести на экран три из них, учитывая следующие условия:
| Слева | По середине | Справа | |
|---|---|---|---|
| Форма фотографии |  |
 |
 |
| Форма шапки |  |
 |
 |
| Число на фотографии | Меньше чем 16 | Больше чем 11 | Точно 8 |
В случае шапки важна её форма, а не цвет.
Какие фотографии появятся на экране?
(Запиши их обозначения в алфавитном порядке, например, ABC.)
[Tekstikast]
Правильный ответ: AGI.
Начнём со всех фотографий и рассмотрим подряд все условия:
| Слева | По середине | Справа |
|---|---|---|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Это задание является примером фильтрации данных по нескольким условиям. Мы можем рассматривать каждый столбец таблицы условий как канал, а каждое условие в этом канале как фильтр, который позволяет продвигать вперёд только те фотографии, которые соответствуют условию, и блокировать все фотографии, которые не соответствуют. Такие многоступенчатые "каналы" в информатике называются конвейерами (англ pipeline) и часто используются для создания более сложных фильтров на базе более простых.
На самом деле конвейеры используются не только для фильтрации данных. Конвейеры также часто состоят из элементов, каждый из которых изменяет данные определённым образом. Например, мы можем создать конвейер, который получает данные об учениках одной школы. Первый этап отображает только дату рождения каждого ученика, на втором этапе каждая дата заменяется соответствующим днём недели, а третий шаг подсчитывает, сколько раз каждый день недели встречался в данных. Таким образом, в конце конвейера мы получим статистику о том, сколько рождённых в каждый день недели детей учится в этой школе.
Хотя каждый элемент конвейера выполнял одну простую операцию, правильно скомбинировав их, мы смогли решить достаточно сложную задачу. В этом и заключается полезность конвейеров.

Коламы — это декоративные узоры, которые можно нарисовать на полу, например, с помощью мела. Чтобы нарисовать колам, сначала отмечают несколько точек, а затем рисуют вокруг них линии. Каждая линия начинается и заканчивается в одной и той же точке, мел во время рисовании не отрывается от пола. Линии могут пересекаться, но они не должны иметь острых углов.
Допускается провести такую дугу:

Такой угол является острым и его рисовать запрещено:

Вот один из примеров рисования колама:
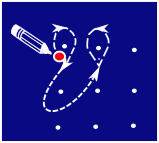
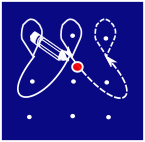
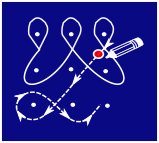
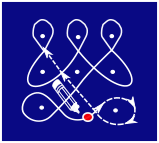

Что из следующего нельзя нарисовать таким образом?
[Raadionupud]
A. 
B. 
C. 
D. 
Правильный ответ: C.
Дизайн вариантов А, B и D непрерывен. Это значит, что при их рисовании мы можем начать с любой точки узора и следовать за кривыми, пока не вернемся к исходной точке.
Вариант С, напротив, состоит из двух отдельных линий, удовлетворяющих условиям колама:


Эту фигуру можно было бы нарисовать и одной линией, но тогда как минимум в двух местах пришлось бы рисовать острый угол, а это не допускается правилами рисования колама.
Коламы — это замысловатые узоры, которые можно найти в индийских городах и деревнях. Как запоминаются и рисуются эти узоры? Одна из теорий гласит, что они создаются по простым правилам, которые передаются из поколения в поколение.
Генерация текстов, которые соответствуют наборам правил, изучается в информатике в рамках теории формальных языков. Хотя изначально генеративные грамматики были предназначены для описания текстов (представляющих из себя одномерные строки символов), позже эта идея была распространена на многомерные объекты, включая графические изображения. Такие методы также часто используются в процедуральном искусстве (англ generative art).

Рассмотрим изображение, состоящее из 6x5 квадратов, где некоторые квадраты красные, а некоторые — белые:
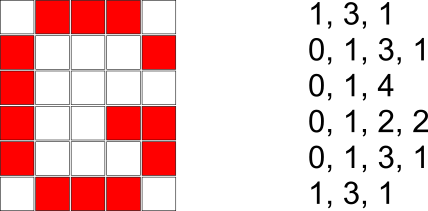
Это изображение можно преобразовать в последовательность чисел, подсчитав для каждой строки, сколько квадратов последовательно окрашено в белый цвет, а затем сколько квадратов последовательно окрашено в красный цвет, далее сколько квадратов последовательно окрашено в белый цвет и т.д., пока мы не достигнем конца строки. Обратите внимание, что если строка начинается с красного квадрата, то количество белых квадратов в начале этой строки равно 0.
В самом конце мы должны объединить все числа, которые получились для каждой строчки, в одну последовательность чисел. В случае вышеприведённого изображения получится следующая последовательность: 1, 3, 1, 0, 1, 3, 1, 0, 1, 4, 0, 1, 2, 2, 0, 1, 3, 1, 1, 3, 1.
Какая последовательность чисел описывает нижеприведённое изображение?

[Raadionupud]
A. 0, 1, 3, 4, 1, 1, 3, 1, 0, 2, 2, 1, 0, 1, 3, 1, 2, 2, 1
B. 1, 3, 1, 4, 1, 1, 4, 0, 1, 3, 1, 0, 1, 3, 1, 1, 3, 1
C. 1, 3, 1, 0, 1, 4, 1, 4, 0, 1, 3, 1, 0, 1, 3, 1, 1, 3, 1
D. 1, 3, 1, 4, 1, 1, 4, 1, 3, 1, 1, 3, 1, 1, 3, 1
Правильный ответ: B.
Чтобы найти ответ, нужно преобразовать как минимум четыре ряда изображения в числа, а затем объединить их:
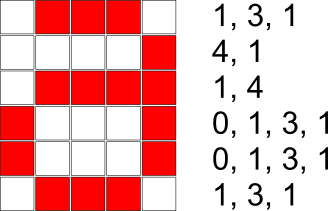
В результате получится последовательность 1, 3, 1, 4, 1, 1, 4, 0, 1, 3, 1, 0, 1, 3, 1, 1, 3, 1, а это соответствует варианту B.
Остальные три ответа относятся к другим изображениям, поскольку для каждого изображения есть только одно характерное исключительно для него представление. Другими словами: разные представления всегда соответствуют разным изображениям.
Для хранения или передачи изображений между электронными устройствами необходимо преобразовать их в числа. Есть много способов сделать это, и в этом задании показан один из них. Используя одно число для представления последовательности квадратов одного и того же цвета, этот метод сжимает данные, т.е. уменьшает объём данных, а это имеет важное значение в информатике. Этот метод можно улучшить несколькими способами, например, позволив числу ссылаться на последовательность, которая охватывает квадраты более чем одной строки.
Поиск способов представления данных был сложной задачей с момента появления первых электронных устройств. Выбор способа может повлиять на время, необходимое для обработки или отправки и получения информации. Сегодня эта проблема по-прежнему актуальна, особенно в Интернете: создание новых способов кодирования изображений, видео и других медиафайлов может ускорить нашу работу в Интернете.
Описанный в этом задании метод использовался старыми факсами для передачи содержания документов.
Copyright © 2022 Bebras – International Challenge on Informatics and Computational Thinking.
Licensed under Creative Commons Attribution-ShareAlike 4.0 International License.
Flag icons by GoSquared.