
Veroonika armastab hüpata. Ta leidis 17 ruutu, mis asetsevad ühel joonel, ja koostas nendest mänguplaani.
Veroonika pani mündi ruudustiku ühte otsa ja seisis ise teise otsa, näoga mündi poole.

Ta soovib hüpata rea igale ruudule, järgides järgmisi reegleid:
Milline mänguplatsi plaanidest viib ta kõigi teiste ruutude külastamise järel mündi juurde?
[Raadionupud]
A. 
B. 
C. 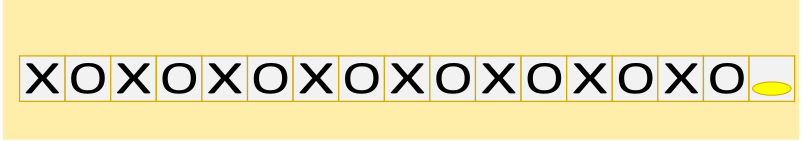
D. 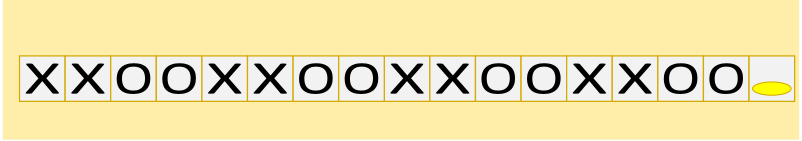
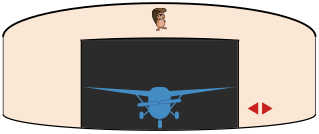
Kopralinna lennuväljal on ümmarguses angaaris asuvale pöörlevale alusele pargitud kuus lennukit. Alust saab pöörata vasakule või paremale, kasutades kahe noolega juhtpaneeli. Ühe nupuvajutusega pööratakse alust täpselt ühe parkimiskoha võrra vastavalt noolele kas vasakule või paremale. Angaari värav on parajasti nii lai, et üks lennuk saaks välja veereda. Alus pöörleb väga aeglaselt, seega mida vähem nupuvajutusi on vaja, seda kiiremini saab töö tehtud.
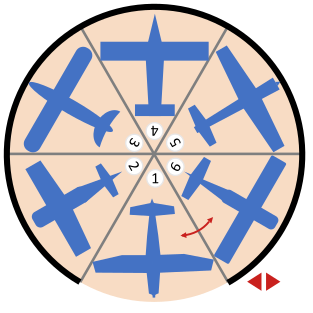
Hommikuti, kui piloodid tulevad lennukitele järele, on värava juures alati parkimiskoht nr 1. Parimal juhul tuleb nooleklahve vajutada viis korda, et kõik lennukid välja veereks. See juhtub siis, kui piloodid soovivad saada parkimiskohtadele järjekorras 1, 2, 3, 4, 5, 6 (siis tuleb viis korda järjest vajutada parempoolsele noolele) või järjekorras 1, 6, 5, 4, 3, 2 (siis tuleb viis korda järjest vajutada vasakpoolsele noolele).
Milline on halvim juhtum ehk milline parkimiskohtadele juurdepääsu järjekord nõuab kõigi lennukite väljaveeremiseks kõige rohkem nupuvajutusi?
(Sisesta kuus erinevat numbrit, näiteks 654321. Kui võimalikke vastuseid on mitu, sisesta ükskõik milline neist.)
[Tekstikast]
Pildil on suusakuurordi kaart koos suusaradade ja suusatõstukitega:
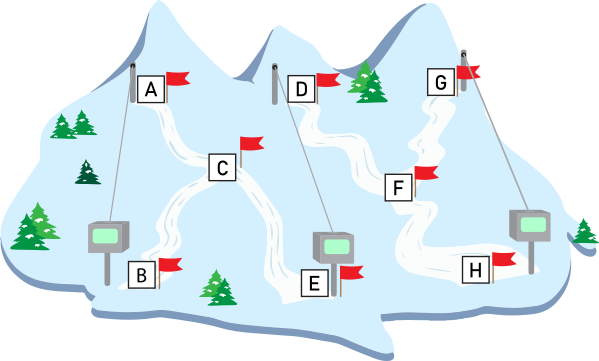
Suusatajad kasutavad ülesmäge sõitmiseks ainult tõstukeid ja allamäge suusatavad ainult mööda kaardil märgitud radu. Kuurordis on kuus suusarada: A-C, C-B, C-E, D-F, F-H ja G-F.
Kopra-Vello vedas sõbraga kihla, et ta suudab suusatada nii, et kasutab iga tõstukit ja iga suusarada täpselt ühe korra ilma vahepeal kuidagi muud moodi ringi liikumata.
Millisest punktist peab Vello alustama, et seda teha?
[Raadionupud]
A. Punktist A
B. Punktist B
C. Punktist C
D. Punktist D
E. Punktist E
F. Punktist F
G. Punktist G
H. Punktist H
Kuuel saarel elav džunglikogukond soovib need saared ühendada, ehitades rippsildade võrgustiku. Selleks tehti võimalike sildade plaan, kus arvud näitavad iga silla ehitamise kulu.
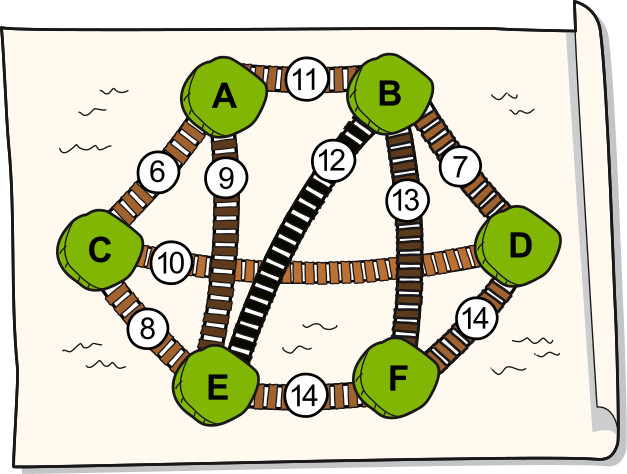
Kogukond soovib ühendada saared sildadega nii, et igalt saarelt oleks võimalik liikuda igale teisele saarele (kas otse või muude saarte kaudu). Samas soovib kogukond ehitada sildu võimalikult odavalt.
Plaanil ristuvad sillad on erinevatel kõrgustel ja vee kohal ühelt sillalt teisele astuda ei saaks.
Kui palju minimaalselt maksab kõigi kuue saare ühendamine?
[Täisarv]
Kaks sõpra, Bob ja Ralph, mängivad mängu. Alustuseks tõmbavad nad paberi alumisse äärde musta joone ja nimetavad seda "maaks". Seejärel joonistavad nad mõned sinised ja punased lõigud, luues hiirekujulise kujundi:
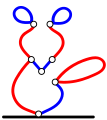
Mängu reeglid on järgmised:
Allpool on toodud üks võimalik käikude jada. Iga käigu kohta on kaks joonist: esimene joonis näitab halli värviga lõiku, mida mängija kavatseb kustutada, teine joonis aga selle kustutamise tulemust.
Bobi käik:
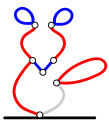
Ralphi käik:
Bobi käik:
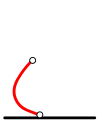
Ralphi käik:


Kuna Bobil pole enam ühtegi lõiku, mida eemaldada, kaotab ta mängu ja Ralph kuulutatakse võitjaks.
Nummerdame sinised lõigud järgmiselt:
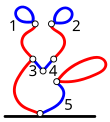
Millise lõigu peaks Bob esimesena kustutama, et kindlasti võita, isegi kui Ralph teeb igas seisus oma parima võimaliku käigu?
[Raadionupud]
A. Lõigu 1
B. Lõigu 2
C. Lõigu 3
D. Lõigu 4
E. Lõigu 5
F. Bobil pole võimalik võita
Kopra-Mati leidis oma toidu jaoks kaks head peidukohta. Meelespidamiseks soovib ta need kaardil ristidega märkida. Aga kui tema rivaal Kati kaardi leiaks, teaks ta, kust otsida!
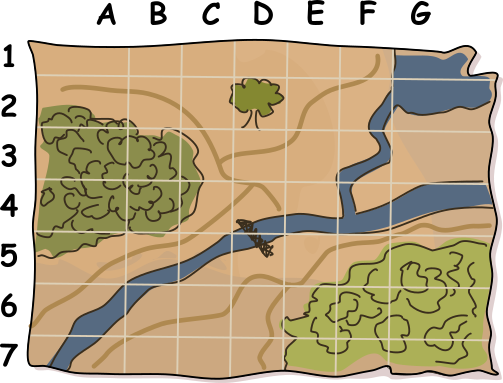
Kati segadusse ajamiseks lisab Mati kaardi teistesse ruutudesse mõned juhuslikud ristid, jälgides, et ristide koguarv igas reas ja veerus oleks paarisarv (tuletame meelde, et ka 0 on paarisarv). Seejärel kustutab ta need kaks risti, mis näitasid tema peidukohti. Valminud kaart on selline:
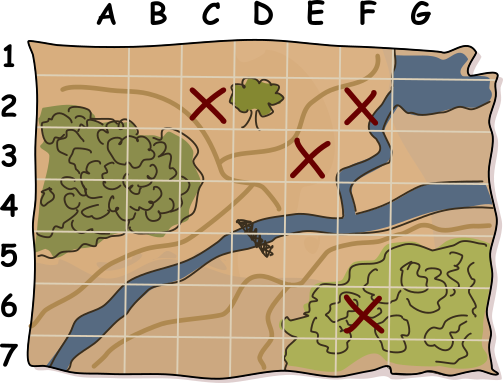
Millistes ruutudes asuvad Mati toiduvarud?
(Kirjuta kahe ruudu tähised, näiteks A1 B2.)
[Tekstikast]
Kaheksanurga igasse tippu on kirjutatud kolm või neli tähte. Must nool osutab kaheksanurga keskpunktist mingile täherühmale. Noolt saab pöörata ainult päripäeva.
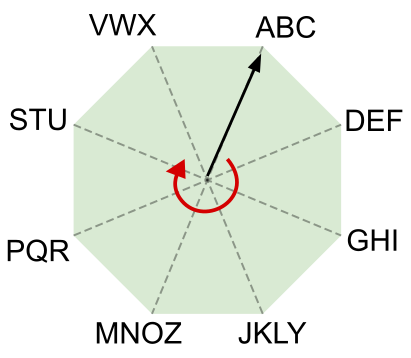
Kasutame seda kaheksanurka ja noolt sõnumite kodeerimiseks. Uue sõnumi kodeerimise alguses osutab nool täherühmale ABC. Edasi kodeerime sõnumi iga tähe nii, et:
Näiteks sõnumi "TREE" kodeerime jadaga 62-73-42-02.
Kuidas me kodeerime sõnumi "WATER"?
[Raadionupud]
A. 72-11-26-32-53
B. 62-11-62-22-43
C. 62-11-26-22-53
D. 72-11-62-32-43
Klassis on 31 tooli. Need asuvad ringikujuliselt ja on nummerdatud arvudega 1 kuni 31, nagu on näha joonisel.
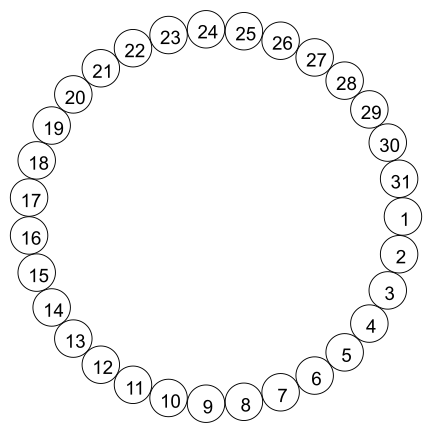
Lapsed mängivad järgmiste reeglitega mängu:
Oletame näiteks, et Teele ja Tuuli on kaksikud, kes on sündinud 20. aprillil, Tõnu on sündinud 21. jaanuaril ja Toomas 22. septembril.
Kui nad saabuvad järjekorras Teele, Tuuli, Toomas, Tõnu, siis istub Teele toolile 20, Tuuli toolile 21, Toomas toolile 22 ja Tõnu toolile 23.
Kui nad saabuvad aga järjekorras Tuuli, Tõnu, Toomas, Teele, siis istub Tuuli toolile 20, Tõnu toolile 21, Toomas toolile 22 ja Teele toolile 23.
Nüüd on klassi sisenenud kuus last ja nad istuvad tabelis näidatud viisil:
| Nimi | Sünnipäev | Tooli number |
|---|---|---|
| Anna | 11. mai | 13 |
| Berta | 12. veebruar | 12 |
| Cathy | 14. september | 14 |
| David | 11. august | 11 |
| Eero | 13. aprill | 15 |
| Feliks | 12. juuli | 16 |
Milline järgmistest väidetest ei saa olla tõene?
[Raadionupud]
A. Cathy istus esimesena
B. Feliks istus viimasena
C. Eero istus enne Annat
D. Berta istus enne Davidit
Anna, Brita, Carolin ja Debora valmistavad suurt hommikusööki. Nad lähevad poodi, et osta nelja toiduainet: mune, vorste, ube ja tomateid.
Kokku teevad nad kaheksa ostu: kaks karpi mune, kaks pakki vorste, kaks purki ube ja kaks tomatit.
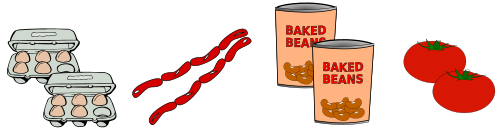
Igaüks neist ostab kahte erinevat tüüpi toiduaineid, samuti on teada, et:
Kui Anna ja Debora ostavad ühe samasuguse toiduaine, siis milline see on?
[Raadionupud]
A. Karp mune
B. Pakk vorste
C. Purk ube
D. Tomat
Neli klotsi on vaja paigutada 2x2 ruuduna tingimusel, et klotsid võivad üksteist puudutada ainult sama sümboliga külgedel. Üks võimalikest viisidest on selline:
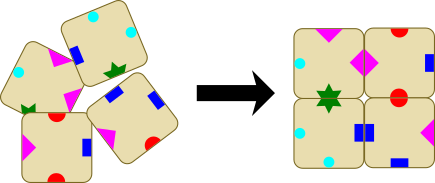
Nüüd on antud aga viis klotsi.

Vaja on nendest viiest valida välja neli klotsi ja paigutada need sama reegli järgi. Käesoleval juhul on ainult üks variant sobiva nelja klotsi valikuks.
Millist klotsi sellisel juhul ei kasutata?
[Raadionupud]
A. Klotsi A
B. Klotsi B
C. Klotsi C
D. Klotsi D
E. Klotsi E
Madis otsib väga pikalt veebilehelt oma sõbra telefoninumbrit. Ta pole kindel, kuidas sõbra nime täpselt kirjutatakse, seepärast kasutab ta otsimisel erimärke:
| Märk | Tähendus |
|---|---|
| ? | täpselt üks tundmatu täht |
| & | täpselt kaks järjestikust tundmatut tähte |
| % | mistahes arv tundmatuid tähti kuni nime lõpuni |
Näiteks otsing "Ma%" leiaks nimed Madis, Marta jne.
Millised järgnevatest nimedest leiab otsing "S?rah B&cht%"?
(Märgi kõik õiged vastused.)
[Märkeruudud]
A. Sarah Birchtree
B. Sara Benchton
C. Sarah Bilchman
D. Sirah Beachtram
Kobras Brunol on arvutustabelis andmed ja valemid.

Nüüd hakkab ta valemitega arvutatud väärtustest (real 3) diagramme joonistama.
Millist allolevatest diagrammidest ta nende andmete põhjal kindlasti ei saa?
[Raadionupud]
A. 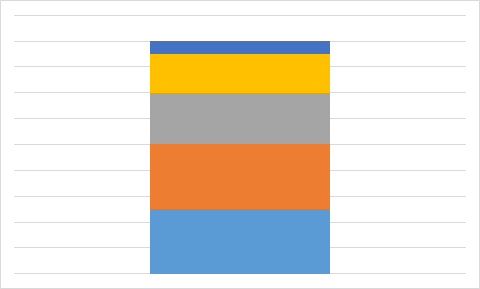
B. 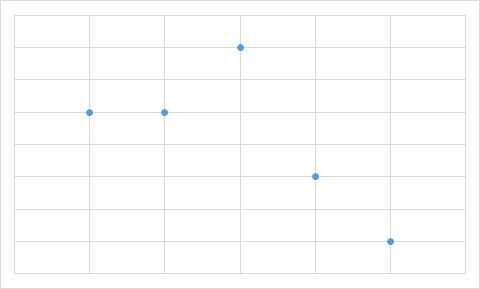
C. 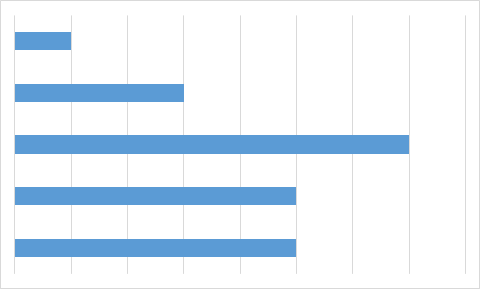
D. 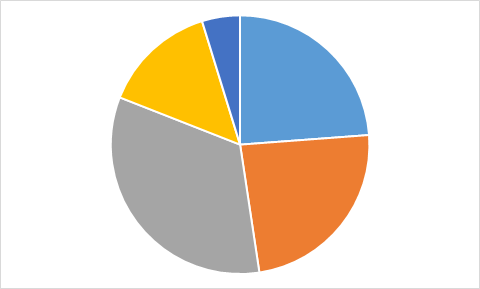
Interneti riidepood kasutab soovituste süsteemi, mis põhineb klientide isikuandmetel. Näiteks kui klient soovib jalatseid osta, järgib programm järgmisel joonisel toodud reeglit ja soovitab saapaid:
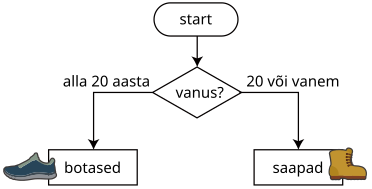
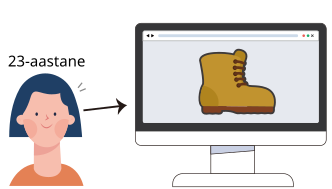
Ühel päeval kustutati osa rõivasoovituse reeglitest kogemata ära. Allolev joonis näitab reeglite allesjäänud osa.

Õnneks on alles ka mõned varem antud soovitused:
| Klient | Soovitus | |
|---|---|---|
| 18-aastane 140 cm |
Ühevärviline seelik |  |
| 32-aastane 145 cm |
Kirju seelik |  |
| 28-aastane 155 cm |
Kirjud püksid |  |
| 15-aastane 160 cm |
Ühevärvilised püksid |  |
| 10-aastane 152 cm |
Ühevärvilised püksid |  |
Milline võis ülaltoodud andmete põhjal olla joonise puuduv osa?
[Raadionupud]
A. 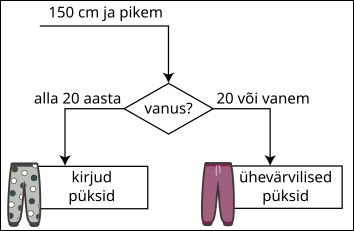
B. 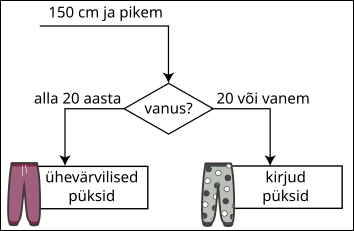
C. 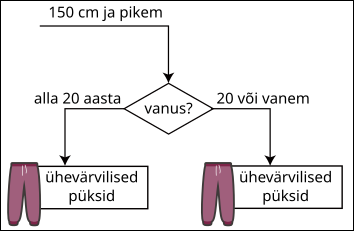
D. 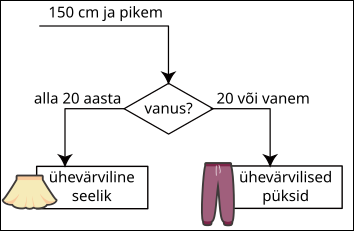
Kolamid on dekoratiivsed mustrid, mida saab põrandale joonistada näiteks kriidiga. Kolami joonistamiseks märgitakse kõigepealt ära mõned punktid ja seejärel tõmmatakse nende ümber jooned. Iga joont alustatakse ja lõpetatakse samas punktis, joonistamise ajal kriiti üles ei tõsteta.
Joon võib ristuda teiste joonte või iseendaga, kuid ei tohi teise joonega kattuda või seda isegi puutuda ilma sellega ristumata. Iga joon peab olema joonistatud vähemalt ühe punkti ümber. Iga sellisel viisil joonistatud joont nimetatakse silmuseks.
Allpool illustreeritud kolamil on 6 silmust. Pange tähele, et silmused ristuvad erinevates kohtades ja musta värvi silmus ristub ka iseendaga.
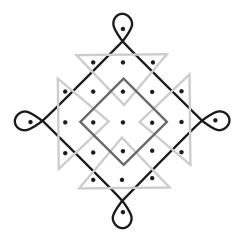
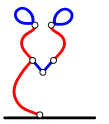
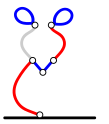
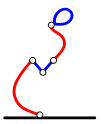
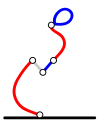
Millisel järgnevatest kolamitest on kõige vähem silmuseid?
[Raadionupud]
A. 
B. 
C. 
D. 
Vaatame 6x5 ruudust koosnevat pilti, mille osad ruudud on mustad, osad valged:
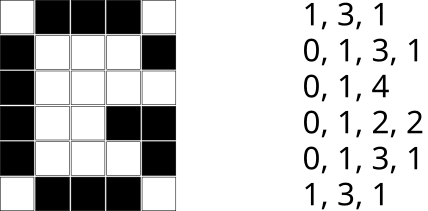
Selle pildi saab teisendada arvujadaks, lugedes iga rea puhul üle, mitu järjestikust ruutu on valged, seejärel mitu järjestikust ruutu on mustad, siis mitu järjestikust ruutu on valged jne, kuni jõuame rea lõppu. Pane tähele, et kui rida algab musta ruuduga, siis on selle rea alguses olevate valgete ruutude arv 0.
Lõpuks ühendame kõigi pildiridade kõik arvud ühte jadasse. Eeltoodud näites oleks tulemuseks selline jada: 1, 3, 1, 0, 1, 3, 1, 0, 1, 4, 0, 1, 2, 2, 0, 1, 3, 1, 1, 3, 1.
Milline 6x5 ruudust koosnev pilt oleks kujutatud jadaga 1, 4, 0, 1, 4, 1, 3, 1, 4, 1, 0, 1, 3, 1, 1, 3, 1?
[Raadionupud]
A. 
B. 
C. 
D. 