

Veroonika armastab hüpata. Ta leidis 17 ruutu, mis asetsevad ühel joonel, ja koostas nendest mänguplaani.
Veroonika pani mündi ruudustiku ühte otsa ja seisis ise teise otsa, näoga mündi poole.

Ta soovib hüpata rea igale ruudule, järgides järgmisi reegleid:
Milline mänguplatsi plaanidest viib ta kõigi teiste ruutude külastamise järel mündi juurde?
[Raadionupud]
A. 
B. 
C. 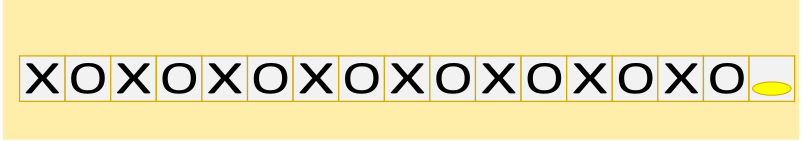
D. 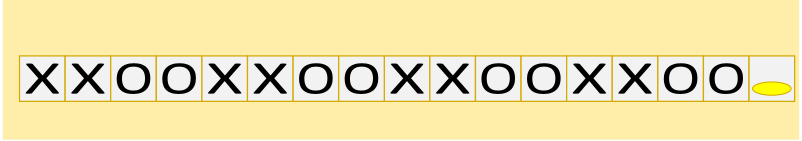
Õige vastus on: D.
Hüppamise järjekord on tähistatud nooltega.
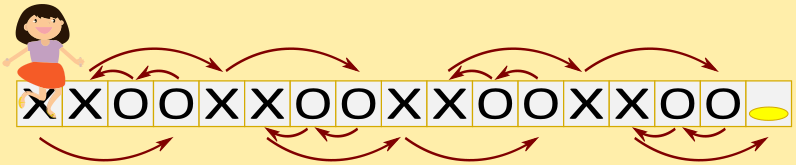
Variandid A ja B ei ole õiged, kuna tüdrukul jääb vahele rea lõpus olev mündiga ruut ning samuti ka vasakult teine ja kolmas ruut. Variant C ei ole õige, kuna ta jätab vahele vasakult teise ruudu.
Toimingute järjekorra leidmist eesmärgi saavutamiseks vastavalt etteantud reeglitele nimetatakse algoritmiseerimiseks. Roboti või arvutirakenduse saab programmeerida nii, et see töötaks etteantud reeglite järgi. Kui vajame tulemuseks konkreetset väljundit, peame määrama ka sobiva sisendi. Oletame, et meil on pikk kitsas L-kujuline koridor ning meie puhastusrobot suudab minna ainult otse ja keerata 90° paremale, peame selle panema L-tähe lühema osa otsa, muidu ei saa tervet koridori puhtaks.

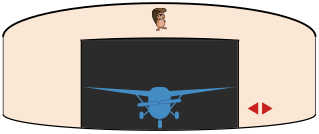
Kopralinna lennuväljal on ümmarguses angaaris asuvale pöörlevale alusele pargitud kuus lennukit. Alust saab pöörata vasakule või paremale, kasutades kahe noolega juhtpaneeli. Ühe nupuvajutusega pööratakse alust täpselt ühe parkimiskoha võrra vastavalt noolele kas vasakule või paremale. Angaari värav on parajasti nii lai, et üks lennuk saaks välja veereda. Alus pöörleb väga aeglaselt, seega mida vähem nupuvajutusi on vaja, seda kiiremini saab töö tehtud.
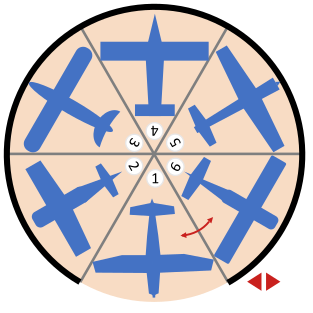
Hommikuti, kui piloodid tulevad lennukitele järele, on värava juures alati parkimiskoht nr 1. Parimal juhul tuleb nooleklahve vajutada viis korda, et kõik lennukid välja veereks. See juhtub siis, kui piloodid soovivad saada parkimiskohtadele järjekorras 1, 2, 3, 4, 5, 6 (siis tuleb viis korda järjest vajutada parempoolsele noolele) või järjekorras 1, 6, 5, 4, 3, 2 (siis tuleb viis korda järjest vajutada vasakpoolsele noolele).
Milline on halvim juhtum ehk milline parkimiskohtadele juurdepääsu järjekord nõuab kõigi lennukite väljaveeremiseks kõige rohkem nupuvajutusi?
(Sisesta kuus erinevat numbrit, näiteks 654321. Kui võimalikke vastuseid on mitu, sisesta ükskõik milline neist.)
[Tekstikast]
Õige vastus on: 413625 või 415263.
Halvimaid järjekordi on kaks: 4, 1, 3, 6, 2, 5 ja 4, 1, 5, 2, 6, 3.
Halvima juhu ja seega ka õige vastuse saab leida, kui valida järgmiseks alati väravast kõige kaugemal asuv mittetühi parkimiskoht. Siin on vaja ette kujutada nii iga pöörde tulemust kui ka seda, kuidas alusel koht koha järel tühjaks saab. Kuna alust saab pöörata mõlemas suunas, on lahendusi rohkem kui üks.
4, 1, 3, 6, 2, 5:
4, 1, 5, 2, 6, 3:
Peaks olema lihtne näha, et ühe või kahe lennuki korral on ainult üks lahendus. Edasi on paarisarvu lennukite korral lahendusi alati kaks, paaritu arvu lennukite korral aga neli. Hea küsimus järele mõtlemiseks: miks see nii on?
Ümmarguse angaari eeliseks on, et see võimaldab ruumi kokku hoida. Aga kuidas on lood ajaga? Kui lennukid on pargitud pilootide saabumise järjekorras, saavad nad kiiresti lennukitesse istuda ja õhku tõusta. Lennukite kättesaamiseks on see parim juhtum, kuid nagu see ülesanne näitas, on enamike protsesside puhul ka halvimad juhud. Halvimal juhul läheb aeg kaotsi, seega tuleb otsustada, kas tähtsam on ruumi või aja kokkuhoid.
Informaatikas on protsessi efektiivsuse hindamine väga oluline. Kuigi probleemi parimaid juhtusid on ka hea teada, on just halvim võimalik juht lahenduse tõhususe iseloomustamisel olulisem. Tõhusus tähendab, et ressursse nagu aeg, energia ja salvestusruum kasutatakse säästlikult.
Tõhusa ladustamise näidet praktiseeritakse tänapäeval postimüügiäris: et kaupadele kiiremini juurde pääseda, ei järjestata neid sageli ei tähestiku ega artiklinumbri järgi; selle asemel võetakse kaupade paigutamisel arvesse, kui sageli neid tavaliselt ostetakse.

Pildil on suusakuurordi kaart koos suusaradade ja suusatõstukitega:
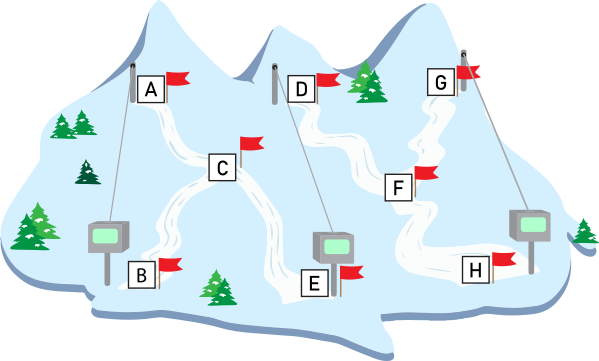
Suusatajad kasutavad ülesmäge sõitmiseks ainult tõstukeid ja allamäge suusatavad ainult mööda kaardil märgitud radu. Kuurordis on kuus suusarada: A-C, C-B, C-E, D-F, F-H ja G-F.
Kopra-Vello vedas sõbraga kihla, et ta suudab suusatada nii, et kasutab iga tõstukit ja iga suusarada täpselt ühe korra ilma vahepeal kuidagi muud moodi ringi liikumata.
Millisest punktist peab Vello alustama, et seda teha?
[Raadionupud]
A. Punktist A
B. Punktist B
C. Punktist C
D. Punktist D
E. Punktist E
F. Punktist F
G. Punktist G
H. Punktist H
Õige vastus on: C (punktist C).
Et kõigist suusaradadest täpselt ühe korra alla sõita ja iga suusatõstukit täpselt ühe korra kasutada, peab punkte läbima järjekorras C, B, A, C, E, D, F, H, G, F.
Järgmisel joonisel on kujutatud suusatõstukid ja suusarajad ning Vello liikumise suund:
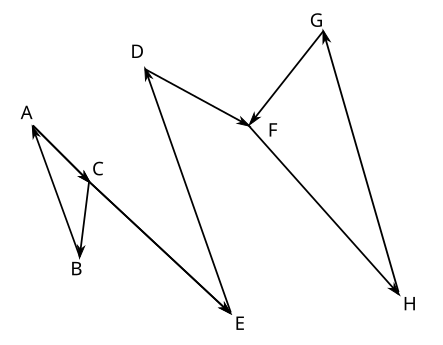
Jooniselt on näha, et igal punktil peale C ja F on täpselt üks sisenev ja üks väljuv tee. Punktil C on kaks väljuvat teed (B ja E suunas), samas kui punktil F on kaks sisenevat teed (punktidest D ja G). See tähendab, et lahendus peab kindlasti algama punktist C ja lõppema punktis F.
Kui alustada punktist C liikumist punkti E suunas, ei ole pärast seda enam võimalik punktidesse A ja B pääseda. Seega on ainus võimalik lahendus alustada punktist C liikumist punkti B suunas. Siis on igal sammul alati üks veel kasutamata rada või tõstuk, millega edasi liikuda.
Vastuse selgituses toodud joonist nimetatakse graafiks (ingl graph). Graafil on tipud (punktid, mis tähistavad lippe) ja servad (jooned, mis tähistavad radu ja tõstukeid). Selle ülesande graaf on suunatud graaf (ingl directed graph, digraph), sest on oluline teada, millises suunas ühest tipust teise saab liikuda; seda näitavad servade otstes olevad nooled.
Graafe kasutatakse informaatikas üsna sageli, et esitada ülesannet abstraktsel kujul. Nagu näeme, võib selline graaf sisaldada ülesande lahendamiseks piisavalt teavet.

Kuuel saarel elav džunglikogukond soovib need saared ühendada, ehitades rippsildade võrgustiku. Selleks tehti võimalike sildade plaan, kus arvud näitavad iga silla ehitamise kulu.
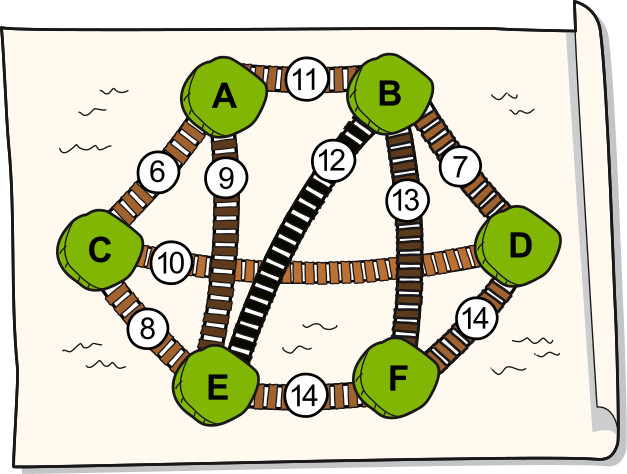
Kogukond soovib ühendada saared sildadega nii, et igalt saarelt oleks võimalik liikuda igale teisele saarele (kas otse või muude saarte kaudu). Samas soovib kogukond ehitada sildu võimalikult odavalt.
Plaanil ristuvad sillad on erinevatel kõrgustel ja vee kohal ühelt sillalt teisele astuda ei saaks.
Kui palju minimaalselt maksab kõigi kuue saare ühendamine?
[Täisarv]
Õige vastus on: 44.
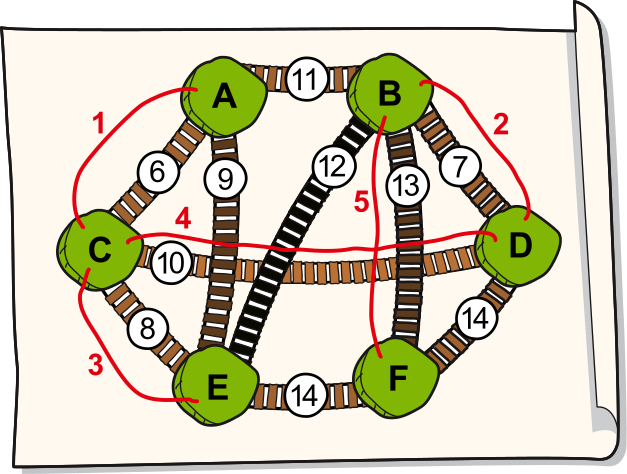
Nüüd on meil kõik kuus saart ühendatud ja selleks ehitatud sildade hinnad kokku on 6+7+8+10+13=44.
Kuidas me aga teame, et see on kõige odavam võimalus?
Esiteks paneme tähele, et kuue saare ühendamiseks on kindlasti vaja viit silda. Iga uus sild ühendab kaks üksust üheks, ehk vähendab üksuste arvu ühe võrra. Alguses on meil iga saar eraldi üksus ja lõpuks on nad kõik ühendatud üheks üksuseks, seega on üksuste arv vähenenud viie võrra. Selle saavutamiseks on meil vaja viit silda.
Teiseks võime iga ehitamata jäetud silla kohta arutada nii: kui me selle silla ehitaks, võiksime ehitamata jätta ühe neist ülejäänud sildadest, millega koos uus sild ringi moodustab; aga nii vahetaks me odavama silla kallima vastu ja sellega läheks ka kõigi sildade ehitamise summa vastavalt suuremaks.
Seega on kindel, et eeltoodud ahne algoritm (ingl greedy algorithm) annab selles ülesandes kindlasti parima võimaliku lahenduse.
Arvutiteaduse seisukohalt on see graafis minimaalse kaaluga aluspuu leidmise ülesanne. Graaf (ingl graph) on struktuur, mis koosneb tippudest (meie ülesandes saared) ja neid ühendavatest servadest (meie ülesandes sillad). Üht graafi nimetatakse teise alamgraafiks, kui selle võib saada teisest graafist mingi hulga servade ja tippude kustutamisega (seejuures võib servi kustutada eraldi, aga tipuga koos kustutatakse alati ära ka kõik sellega seotud servad).
Graafi aluspuuks (ingl spanning tree) nimetatakse sellist alamgraafi, milles on alles kõik tipud ja parasjagu niipalju servi, et igast tipust igasse teise on täpselt üks tee. Graafi aluspuu kaaluks nimetatakse allesjäänud servade kaalude (meie ülesandes sildade hinnad) summat.
Graafi aluspuu leidmiseks on teada mitu meetodit. Eelpool kirjeldatud algoritm (lisame servi nende kaalude kasvamise järjekorras, jättes lisamata ainult need, mis tekitaks tsükli) on tundud Kruskali algoritmi (ingl Kruskal's algorithm) nime all.

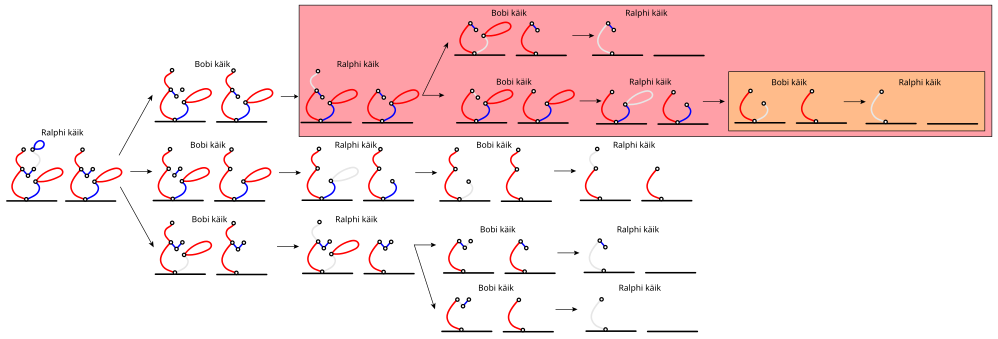
Kaks sõpra, Bob ja Ralph, mängivad mängu. Alustuseks tõmbavad nad paberi alumisse äärde musta joone ja nimetavad seda "maaks". Seejärel joonistavad nad mõned sinised ja punased lõigud, luues hiirekujulise kujundi:
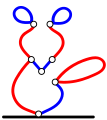
Mängu reeglid on järgmised:
Allpool on toodud üks võimalik käikude jada. Iga käigu kohta on kaks joonist: esimene joonis näitab halli värviga lõiku, mida mängija kavatseb kustutada, teine joonis aga selle kustutamise tulemust.
Bobi käik:
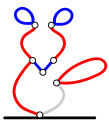
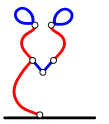
Ralphi käik:
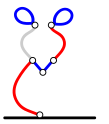
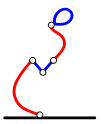
Bobi käik:
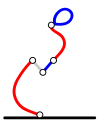
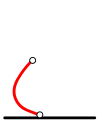
Ralphi käik:


Kuna Bobil pole enam ühtegi lõiku, mida eemaldada, kaotab ta mängu ja Ralph kuulutatakse võitjaks.
Nummerdame sinised lõigud järgmiselt:
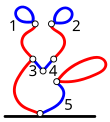
Millise lõigu peaks Bob esimesena kustutama, et kindlasti võita, isegi kui Ralph teeb igas seisus oma parima võimaliku käigu?
[Raadionupud]
A. Lõigu 1
B. Lõigu 2
C. Lõigu 3
D. Lõigu 4
E. Lõigu 5
F. Bobil pole võimalik võita
Õige vastus on: B (lõigu 2).
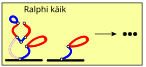
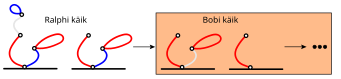
Tõestamaks, et 2. lõigu eemaldamine tagab Bobi võidu, valime kõigepealt ühe Ralphi võimaliku vastuse sellele avakäigule. Sealt edasi mängime mänge tervikuna süstemaatiliselt läbi, kuni leiame võitnud käikude jada (või strateegia). Allolev joonis näitab võidustrateegiat, kui Ralph eemaldab "näo" vasaku poole:

Pimesi mängimise vältimiseks on Bobil kasulik sundida Ralph seisu, mis on olemas eeltoodud võidustrateegias, kuna see võimaldab Bobil võitu kindlustada, kasutades sama käikude jada nagu eeltoodud strateegias. Järgmistel joonistel on need olukorrad tähistatud erinevat värvi ristkülikutega, mis illustreerivad, kuidas nimetatud ideed saab rakendada Ralphi järelejäänud vastuste vastu Bobi avakäigule:
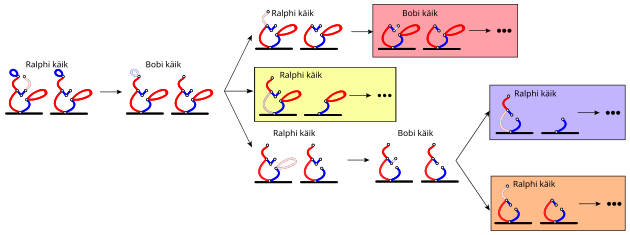
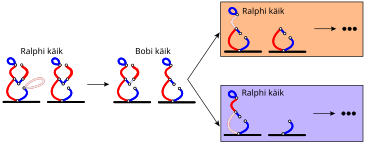
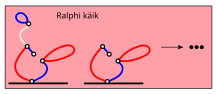
Täielikkuse huvides võib ka näidata, et Bobil pole võiduvõimalust, kui ta alustab mõne teise lõigu kustutamisega ja Ralph valib igal käigul enda jaoks ideaalse vastuse:
Selles ülesandes esitatud mäng (tuntud ka kui Hackenbush, https://en.wikipedia.org/wiki/Hackenbush) kuulub nn kombinatoorsete mängude hulka. Need on kahe mängijaga mängud, mis vastavad kolmele kriteeriumile:
Populaarsed selliste mängude on näited male, kabe, go ja trips-traps-trull.
Kombinatoorsed mängud on informaatika (eriti teoreetilise arvutiteaduse ja tehisintellekti) jaoks väga väärtuslikud uurimisobjektid. Huvivaldkondadeks on võitja väljaselgitamine, kui mõlemad pooled mängivad alati parima võimaliku käigu (nn täiuslik mäng), strateegiate leidmine võiduvõimaluste maksimeerimiseks ja heuristika, et hinnata, kummal mängijal on antud seisus eelis.
Selliste mängude analüüsimiseks saab kasutada nn mängupuid (ingl game tree), mis kirjeldavad kõiki võimalikke seise ja igas seisus võimalikke käike. Mängudes võib aga olla väga palju võimalikke seise, mis muudab kogu mängupuu genereerimise ebaefektiivseks või isegi võimatuks. Sellega toime tulekuks on välja töötatud algoritmid, mis väldivad samade positsioonide mitmekordset uurimist (nagu tegime oma lahenduses) või "kärbivad" mängupuud sellega, et ei uuri edasi seise, mille hinnangud on mingist lävendist halvemad. Tehisintellektis uuritakse selliseid tehnikaid nagu stiimulõpe (ingl reinforcement learning), kus arvutit treenitakse "oma vigadest õppides" ja parandatakse nii otsuste langetamist keeruliste mängude (nt male ja go) puhul.

Kopra-Mati leidis oma toidu jaoks kaks head peidukohta. Meelespidamiseks soovib ta need kaardil ristidega märkida. Aga kui tema rivaal Kati kaardi leiaks, teaks ta, kust otsida!
Kati segadusse ajamiseks lisab Mati kaardi teistesse ruutudesse mõned juhuslikud ristid, jälgides, et ristide koguarv igas reas ja veerus oleks paarisarv (tuletame meelde, et ka 0 on paarisarv). Seejärel kustutab ta need kaks risti, mis näitasid tema peidukohti. Valminud kaart on selline:
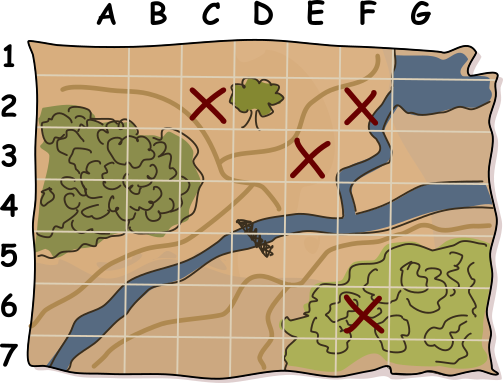
Millistes ruutudes asuvad Mati toiduvarud?
(Kirjuta kahe ruudu tähised, näiteks A1 B2.)
[Tekstikast]
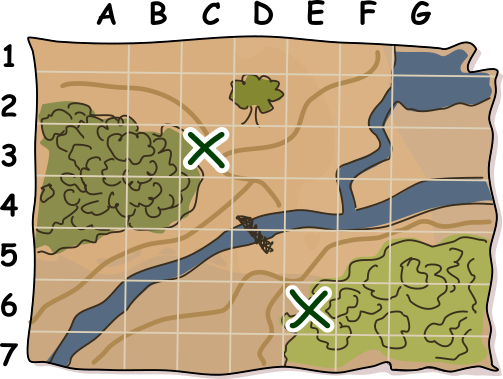
Õige vastus on: C3 E6.
Siin on kahe peidukoha asukohad:
Nende leidmiseks vaatame lõplikku kaarti ja leiame, et seal on kaks rida ja kaks veergu, kus ristide arv pole paaris, nendeks on read 3 ja 6 ning veerud C ja E. Järgneval joonisel on need read ja veerud tähistatud kollase värviga:
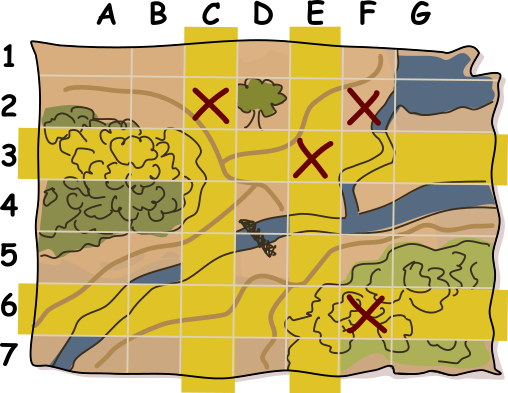
Kaks kustutatud risti peavad olema niisiis nendes ridades ja veergudes, me peame leidma viisi, kuidas need uuesti lisada, et taastada paarisarvulisuse omadus.
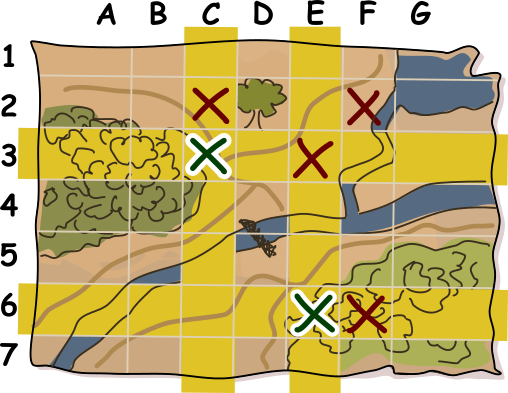
Kollaste ridade ja veergude ristumiskohti on neli. Neist ülemine parempoolne (E3) on juba tähistatud ristiga, seega ei saa see olla peidukohaks: teame, et Mati on tegelikke peidukohti tähistavad ristid kustutanud. Nii peame selleks, et taastada paarisarv riste real 3, lisama risti ülemisse vasakpoolsesse ristumisruutu ehk ruutu C3. Nüüd teame ühte peidukohta.
Teise peidukoha rist ei saa olla alumises vasakpoolses ristumisruudus ehk ruudus C6, kuna tulemuseks oleks 3 risti veerus C ja 3 pole paarisarv. Ainus valik on alumine parempoolne ristumisruut ehk E6. Nii saamegi ülaltoodud vastuse.
Siin on kaart, nagu ta oli enne ristide kustutamist, ja tõesti on paarisarv riste igas reas ja igas veerus:
Mati kasutab siin võtet, mis on seotud arvutiteaduses sageli tarvitatava paarsusbiti mõistega. See on osa suuremast hulgast võtetest, mis on tuntud vigade tuvastamise ja parandamise meetoditena. Idee seisneb selles, et kui me peame salvestama või edastama andmeid bittide (ühtede ja nullide) jadana, lisame jadale täiendavaid bitte, mis aitavad meil tuvastada, kas edastusel või salvestamisel on tekkinud vigu, näiteks selliseid, kus saadeti 1, aga vastu võeti 0.
Kui kasutame lihtsat veatuvastuskoodi, võime lisada paarsusbiti, nii et ühtede arv oleks paaris. Nii lisame jadale "0110101" nulli, et saada jada "01101010" ja ühtede arv jadas jääks paarisarvuks. Kui näiteks teine bitt võeti valesti vastu ning saadi hoopis jada "00101010", siis vastuvõetud sõnum ei vasta meie paarsusnõudele (jadas on paaritu arv ühtesid). Paneme tähele, et kui vigaseid bitte on rohkem kui üks, ei pruugi selline lihtne meetod probleemi tuvastada.

Kaheksanurga igasse tippu on kirjutatud kolm või neli tähte. Must nool osutab kaheksanurga keskpunktist mingile täherühmale. Noolt saab pöörata ainult päripäeva.
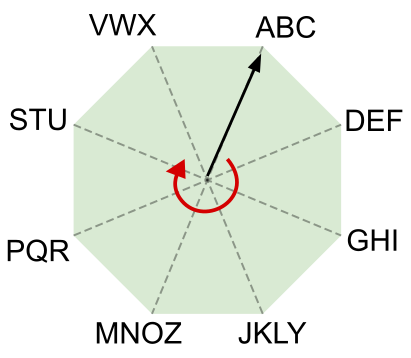
Kasutame seda kaheksanurka ja noolt sõnumite kodeerimiseks. Uue sõnumi kodeerimise alguses osutab nool täherühmale ABC. Edasi kodeerime sõnumi iga tähe nii, et:
Näiteks sõnumi "TREE" kodeerime jadaga 62-73-42-02.
Kuidas me kodeerime sõnumi "WATER"?
[Raadionupud]
A. 72-11-26-32-53
B. 62-11-62-22-43
C. 62-11-26-22-53
D. 72-11-62-32-43
Õige vastus on: D (72-11-62-32-43).
Õige vastuse saame, kodeerides sõnumi "WATER" tähthaaval. Sõnumi kood sisaldab 5 numbripaari:
Sõnumi kood on seega 72-11-62-32-43.
Üks meetod andmete kaitsmiseks volitamata isikute eest on šifreerimine. Salakirjateadus e krüptograafia (ingl cryptography) sai alguse juba 3500 aastat tagasi. Üks lihtsamaid šifreid on iga tähe asendamine mingi teise tähega. Selline nn asendusšiffer (ingl substitution cipher) on kergesti lahti murtav, kuna igas keeles on erinevate tähtede esinemissagedused erinevad ja selle põhjal on üsna lihtne tuvastada enamkasutatavate tähtede koodid.
Meie ülesandes on kasutusel meetod, mis noole pöörlemise tõttu annab ühe tähe jaoks erinevad koodid vastavalt sellele, milline täht on sõnumis eelmine. Sellega tekib šifris mõningane varieeruvus ja seda on raskem lahti murda. Samas on šiffer aga piisavalt lihtne, et seda kergesti meelde jätta.
Kui me jagaks tähed gruppidesse teistmoodi või paigutaks gruppe kaheksanurga tippudesse teises järjekorras, saaksime samale sõnumile erinevaid koode. Šifreerimisskeemi sellist seadistust nimetatakse šifreerimisvõtmeks (ingl encryption key) ja selle äraarvamist krüptoanalüüsiks (ingl cryptoanalysis).

Klassis on 31 tooli. Need asuvad ringikujuliselt ja on nummerdatud arvudega 1 kuni 31, nagu on näha joonisel.
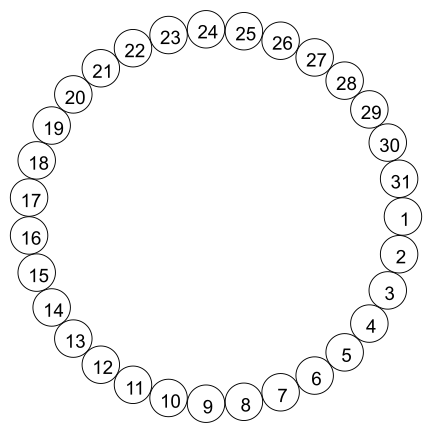
Lapsed mängivad järgmiste reeglitega mängu:
Oletame näiteks, et Teele ja Tuuli on kaksikud, kes on sündinud 20. aprillil, Tõnu on sündinud 21. jaanuaril ja Toomas 22. septembril.
Kui nad saabuvad järjekorras Teele, Tuuli, Toomas, Tõnu, siis istub Teele toolile 20, Tuuli toolile 21, Toomas toolile 22 ja Tõnu toolile 23.
Kui nad saabuvad aga järjekorras Tuuli, Tõnu, Toomas, Teele, siis istub Tuuli toolile 20, Tõnu toolile 21, Toomas toolile 22 ja Teele toolile 23.
Nüüd on klassi sisenenud kuus last ja nad istuvad tabelis näidatud viisil:
| Nimi | Sünnipäev | Tooli number |
|---|---|---|
| Anna | 11. mai | 13 |
| Berta | 12. veebruar | 12 |
| Cathy | 14. september | 14 |
| David | 11. august | 11 |
| Eero | 13. aprill | 15 |
| Feliks | 12. juuli | 16 |
Milline järgmistest väidetest ei saa olla tõene?
[Raadionupud]
A. Cathy istus esimesena
B. Feliks istus viimasena
C. Eero istus enne Annat
D. Berta istus enne Davidit
Õige vastus on: C (Eero istus enne Annat).
Cathy istub oma sünnipäevale vastaval toolil, nii et ta võis olla esimesena siseneja. Seega variant A võib olla tõene väide.
Selleks, et maanduda toolil 16, pidi Feliks saabuma pärast neid, kes istuvad toolidel 12–15. David istub toolil 11, seega pidi ta saabuma enne Annat, kellel on temaga sama sünnikuupäev. Seega on variant B kindlasti tõene väide.
Kui Eero oleks tulnud enne Annat, oleks tool 13 olnud vaba ja Eerol poleks olnud vaja istuda toolile 15. Seega ei saa variant C olla õige.
Berta ja David istuvad mõlemad oma sünnikuupäevale vastavatel toolidel ja võisid saabuda ükskõik kummas järjekorras. Seega variant D võib olla õige väide.
Räsimine (ingl hashing) on meetod suure hulga võimalike sisendväärtuste jagamiseks fikseeritud väljundväärtuste hulgale. Selles ülesandes on sisendhulk kõigi sünnipäevade kogum ja väljundhulk toolid numbritega 1 kuni 31. Räsifunktsioon arvutab iga sisendi põhjal väljundi. Kui sisendhulk on suurem kui väljundhulk, võidakse kahe sisendiga vastavusse panna sama väljund, seega peame pakkuma mehhanismi selliste kokkupõrgete (ingl collision) lahendamiseks. Ülesanne kirjeldab lahendust nimega avatud adresseerimine, mille puhul suunatakse kokkupõrke korral hilisem saabuja väljundhulgas järgmistele väärtustele. Räsimist ja selle erinevaid kokkupõrgete lahendamise viise kasutatakse andmete salvestamisel paisktabelites (ingl hash table).

Anna, Brita, Carolin ja Debora valmistavad suurt hommikusööki. Nad lähevad poodi, et osta nelja toiduainet: mune, vorste, ube ja tomateid.
Kokku teevad nad kaheksa ostu: kaks karpi mune, kaks pakki vorste, kaks purki ube ja kaks tomatit.
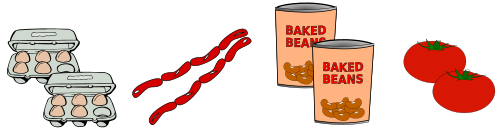
Igaüks neist ostab kahte erinevat tüüpi toiduaineid, samuti on teada, et:
Kui Anna ja Debora ostavad ühe samasuguse toiduaine, siis milline see on?
[Raadionupud]
A. Karp mune
B. Pakk vorste
C. Purk ube
D. Tomat
Õige vastus on: A (munad).
Ülesande lahendamiseks koostame samm-sammult tõeväärtustabeli.
Esimene väide ütleb, et Anna ostab mune, aga Brita mitte.
| Anna | Brita | Carolin | Debora | |
|---|---|---|---|---|
| Munad | 1 | 0 | ||
| Vorstid | ||||
| Oad | ||||
| Tomat |
Teine väide ütleb, et Carolin ja Brita ostavad ube. Kuna ube ostetakse ainult kaks purki, ei osta neid seega ei Anna ega Debora.
| Anna | Brita | Carolin | Debora | |
|---|---|---|---|---|
| Munad | 1 | 0 | ||
| Vorstid | ||||
| Oad | 0 | 1 | 1 | 0 |
| Tomat |
Hüpates neljanda väite juurde, siis see ütleb meile, et Brita ei osta vorste. Kuna Brita peab ostma kaks kaupa ja ta ei osta mune ega vorsti, peab ta ostma tomati.
| Anna | Brita | Carolin | Debora | |
|---|---|---|---|---|
| Munad | 1 | 0 | ||
| Vorstid | 0 | |||
| Oad | 0 | 1 | 1 | 0 |
| Tomat | 1 |
Kolmas väide ütleb meile, et Debora ja Carolin ostavad ühe ühise toiduaine. Kuna ühe karbi mune ostab Anna, ei ole see kaup munad. Kuna Brita ostab ühe oapurgi ja ühe tomati, siis pole selleks toiduaineks ka ei oad ega tomatid. Ainus võimalus on, et Debora ja Carolini ühine ost on vorstid.
| Anna | Brita | Carolin | Debora | |
|---|---|---|---|---|
| Munad | 1 | 0 | ||
| Vorstid | 0 | 0 | 1 | 1 |
| Oad | 0 | 1 | 1 | 0 |
| Tomat | 1 |
Nüüd saame Anna veeru lõpule viia. Anna peab teise kaubana ostma tomati ja kuna ostetakse ainult kaks tomatit, ei saa ei Carolin ega Debora tomatit osta.
| Anna | Brita | Carolin | Debora | |
|---|---|---|---|---|
| Munad | 1 | 0 | ||
| Vorstid | 0 | 0 | 1 | 1 |
| Oad | 0 | 1 | 1 | 0 |
| Tomat | 1 | 1 | 0 | 0 |
Nüüd saame täita kogu tabeli. Kuna meil on juba teada kaks asja, mille Carolin ostab, siis seega ei saa ta osta mune ning järelikult ostab munad Debora.
| Anna | Brita | Carolin | Debora | |
|---|---|---|---|---|
| Munad | 1 | 0 | 0 | 1 |
| Vorstid | 0 | 0 | 1 | 1 |
| Oad | 0 | 1 | 1 | 0 |
| Tomat | 1 | 1 | 0 | 0 |
Seega kui küsida, mida Anna ja Debora ühist ostavad, ütleb täidetud tabel, et tegemist on munadega.
Selle ülesande lahendamiseks on ka teisi võimalikke viise. Näiteks võime kaaluda antud fakte teises järjekorras ja täita tabeli lahtreid teises järjekorras. Info loogilisel esitusel on samuti mitu võimalust. Näiteks võib selleks tõeväärtustabeli asemel kasutada graafi, mis visualiseeriks andmeid teistmoodi.
See ülesanne on näide loogikaülesandest. Antud on osaline teave selle kohta, mida neli sõpra poest ostsid, ja selle teabe põhjal saame deduktiivse arutluskäigu abil välja selgitada, millise toiduaine Anna ja Debora ühiselt ostsid. Loogika on ka programmeerimise oluline osa. Kõige otsesemalt kasutame loogikat programmides tingimuste (if-lausete) koostamisel, kuid loogikat saab kasutada näiteks ka otsinguruumi vähendamiseks, et programm saaks ülesande palju tõhusamalt lahendada.
Selle ülesande lahendamiseks oli kasulik koostada tõeväärtuste tabel. Tabeliesituse pluss on, et see tuletab meelde, milline info meil veel puudub. Sageli aitab hea andmete esitusviisi valik ülesannet hõlpsamini lahendada ka programmeerimises.

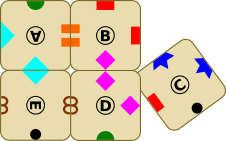
Neli klotsi on vaja paigutada 2x2 ruuduna tingimusel, et klotsid võivad üksteist puudutada ainult sama sümboliga külgedel. Üks võimalikest viisidest on selline:
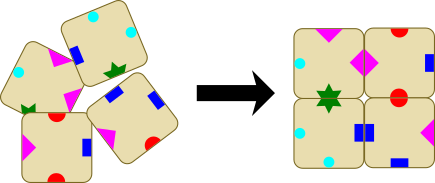
Nüüd on antud aga viis klotsi.

Vaja on nendest viiest valida välja neli klotsi ja paigutada need sama reegli järgi. Käesoleval juhul on ainult üks variant sobiva nelja klotsi valikuks.
Millist klotsi sellisel juhul ei kasutata?
[Raadionupud]
A. Klotsi A
B. Klotsi B
C. Klotsi C
D. Klotsi D
E. Klotsi E
Õige vastus on: C (klotsi C).
On võimalik luua 2x2 ruut, mis järgib antud reeglit, kasutades klotse A, B, D ja E:
Üks võimalus on proovida erinevaid variante, kuni üks sobib, kuid kontrollitavate kombinatsioonide arvu saab ka vähendada.
Teeme seda kahes eraldi etapis.
Esiteks koostame viiest klotsist graafi ja ühendame joontega need klotsid, millel on vähemalt üks samasugune sümbol. Näiteks C ja E ühendame joonega selletõttu, et mõlema ühel küljel on väike must ring, samas A ja C pole ühendatud, kuna ükski klotsil A olevatest sümbolitest ei esine klotsil C.
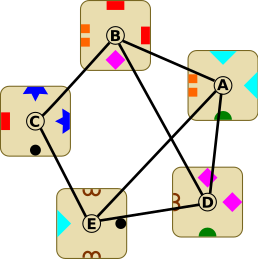
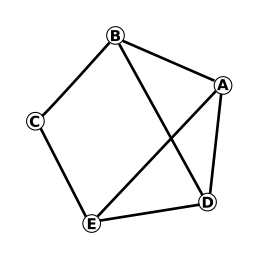
Kui leiame tee klotsist klotsini, mis jõuab pärast nelja sammu esimese klotsini tagasi, oleme leidnud võimaliku lahenduse.
Teiseks selgitame abiskeemi abil välja kõikvõimalikud nelja sammu pikkused tsüklid. Meie graafis on kolm sellist tsüklit:
Loomulikult on samaväärsed kõik viie tähe tsüklilised permutatsioonid (st alustades suvalisest tähest, kuid säilitades järjekorra) ja ka nende tagurpidised variandid, näiteks A-B-C-E-A, B-C-E-A-B ja E-C-B-A-E on samaväärsed.
Kas on võimalik, et teine või kolmas abiskeemiga leitud variantidest (A-B-C-E-A või B-C-E-D-B) viib ka meie mõistatuse lahenduseni?
Mõlemad tsüklid sisaldavad kolmikut B-C-E ja nende klotside ühendamiseks selles järjekorras on ainult kaks võimalust:
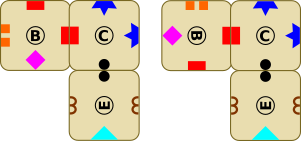
Kummalgi juhul aga ei saa neljandana kasutada ei klotsi A ega klotsi D.
Need võõrlahendid tekkisid eelmisel sammul sellest, et me graafi koostamisel arvestasime ainult seda, millised kujundid igal klotsil esinevad, aga eirasime nende kujundite paigutust klotsidel.
Probleemi lahendamiseks on sageli kasulik (ajutiselt) ignoreerida mõningaid selle detaile, seda nimetatakse abstraktsiooniks. Esimeses etapis eirasime sümbolite asukohti klotsidel, meid huvitas ainult see, kas kahel klotsil on ühiseid sümboleid või mitte. Saadud skeem (graaf) andis meile juba piisavalt teavet, et muuta lahenduse otsimine pisut lühemaks, alles jäi vaid kolm võimalikku lahendust.
Graafe kasutatakse informaatikas sageli töödeldavate andmete abstraktsioonina. Ajaloo jooksul on paljud inimesed kasutanud nutikaid ja kiireid meetodeid selliste graafide erinevate omaduste määramiseks, näiteks kõigi teatud pikkusega tsüklite hõlpsaks leidmiseks.
Ülesande edasiseks lahendamiseks vajasime teist sammu, mis jällegi kasutas ülesande abstraktsioonina graafi. Raske probleemi jagamist eraldi etappideks, mida saab lihtsamini lahendada, nimetatakse dekompositsiooniks: taas oluline arvutusliku mõtlemise oskus.

Madis otsib väga pikalt veebilehelt oma sõbra telefoninumbrit. Ta pole kindel, kuidas sõbra nime täpselt kirjutatakse, seepärast kasutab ta otsimisel erimärke:
| Märk | Tähendus |
|---|---|
| ? | täpselt üks tundmatu täht |
| & | täpselt kaks järjestikust tundmatut tähte |
| % | mistahes arv tundmatuid tähti kuni nime lõpuni |
Näiteks otsing "Ma%" leiaks nimed Madis, Marta jne.
Millised järgnevatest nimedest leiab otsing "S?rah B&cht%"?
(Märgi kõik õiged vastused.)
[Märkeruudud]
A. Sarah Birchtree
B. Sara Benchton
C. Sarah Bilchman
D. Sirah Beachtram
Õige vastus on: A, D.
Variant A on õige, sest nimi "Sarah Birchtree" vastab otsingule "S?rah B&cht%":
Variant B ei ole õige, sest eesnimes "Sara" ei ole "h"-tähte.
Variant C ei ole õige, sest perenimes "Bilchman" on "cht" asemel "chm".
Variant D on õige, sest "S" ja "S", "i" ja "?", "rah" ja "rah", tühik ja tühik, "B" ja "B", "ea" ja "&", "cht" ja "cht" ning "ram" ja "%" kõik vastavad.
Paljud infosüsteemid võimaldavad info otsimiseks kasutada selles ülesandes kirjeldatud erimärkidele sarnaseid nn metamärke (ingl wildcard) ehk jokkereid. Näiteks nii Windowsi, MacOSi kui Linuxi paljudes käskudes on võimalik mitme faili korraga nimetamiseks kasutada "?" tähenduses "täpselt üks tundmatu märk" ja "*" tähenduses "mistahes arv tundmatuid märke".
Teise näitena lubavad paljud tekstitöötlusprogrammid teksti otsimisel ja ka asendamisel kasutada mustrite kirjeldamiseks nn regulaaravaldisi (ingl regular expression).
Sellised vahendid võimaldavad aega kokku hoida, sest nii saab käske rakendada korraga paljudele failidele või sõnadele. Ilma nendeta tuleks käsk anda kas iga faili või iga võimaliku sõna kohta eraldi.

Kobras Brunol on arvutustabelis andmed ja valemid.

Nüüd hakkab ta valemitega arvutatud väärtustest (real 3) diagramme joonistama.
Millist allolevatest diagrammidest ta nende andmete põhjal kindlasti ei saa?
[Raadionupud]
A. 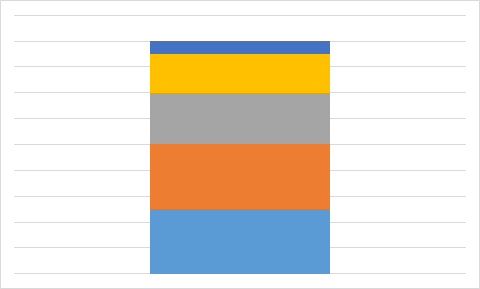
B. 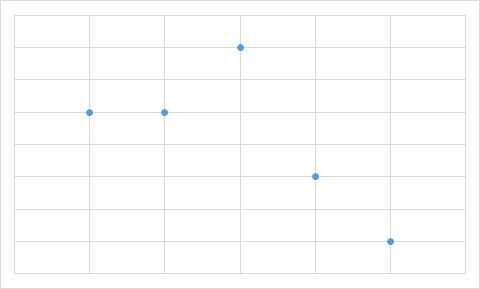
C. 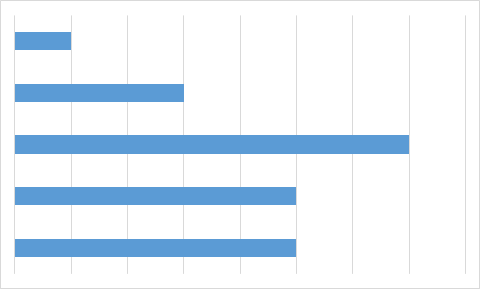
D. 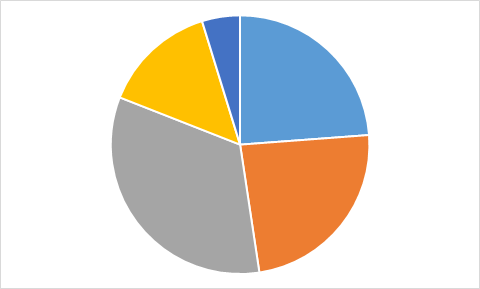
Õige vastus on: A.
Vastuse leidmiseks pole isegi vaja kõigi valemilahtrite väärtusi välja arvutada. Piisab tähelepanekust, et kolmel diagrammil on üks väärtus kõige suurem ja selle järel suuruselt teisi väärtusi kaks võrdset, aga diagrammil A on just maksimaalse suurusega väärtusi kaks võrdset. Seega ei ole diagramm A kindlasti koostatud samadest andmetest, millest ülejäänud.
Andmete töötlemisel võib kergesti juhtuda, et midagi läheb valesti. Sellepärast on alati kasulik oma töö tulemusele peale vaadata ja mõelda, kas seal on midagi, mis ilmselgelt ei klapi või ei sobi.

Interneti riidepood kasutab soovituste süsteemi, mis põhineb klientide isikuandmetel. Näiteks kui klient soovib jalatseid osta, järgib programm järgmisel joonisel toodud reeglit ja soovitab saapaid:
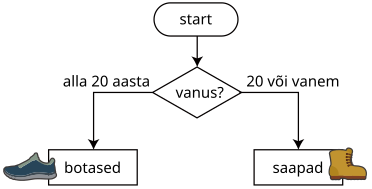
Ühel päeval kustutati osa rõivasoovituse reeglitest kogemata ära. Allolev joonis näitab reeglite allesjäänud osa.

Õnneks on alles ka mõned varem antud soovitused:
| Klient | Soovitus | |
|---|---|---|
| 18-aastane 140 cm |
Ühevärviline seelik |  |
| 32-aastane 145 cm |
Kirju seelik |  |
| 28-aastane 155 cm |
Kirjud püksid |  |
| 15-aastane 160 cm |
Ühevärvilised püksid |  |
| 10-aastane 152 cm |
Ühevärvilised püksid |  |
Milline võis ülaltoodud andmete põhjal olla joonise puuduv osa?
[Raadionupud]
A. 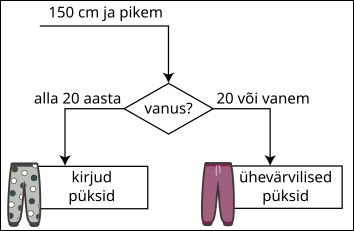
B. 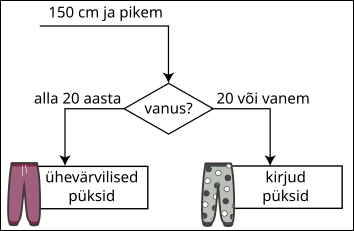
C. 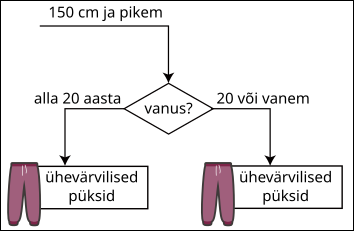
D. 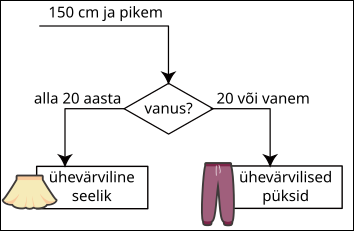
Õige vastus on: B.
Esimene tingimus kontrollib kliendi pikkust, seega peame arvestama ainult vähemalt 150 cm pikkuste klientidega:
| Klient | Soovitus | |
|---|---|---|
| 28-aastane 155 cm |
Kirjud püksid |  |
| 15-aastane 160 cm |
Ühevärvilised püksid |  |
| 10-aastane 152 cm |
Ühevärvilised püksid |  |
Tabelist näeme, et kõigil neil klientidel soovitati osta pükse, seetõttu on variant D vale.
Kuna kõigile alla 20-aastastele klientidele soovitati ühevärvilisi pükse, on variant A vale.
Kuna kõigile 20-aastastele ja vanematele klientidele soovitati kirjusid pükse, on variant C vale.
Näeme, et pikemad kliendid said vastavalt vanusele erinevaid püksisoovitusi, seetõttu peaks täielik joonis välja nägema selline:

Joonist, mida programm selles ülesandes järgib, nimetatakse otsustuspuuks (ingl decision tree). See on vooskeemi (ingl flowchart) lihtsam erijuht.
Informaatikas saab vooskeemi kasutada algoritmi, töövoo või protsessi esitamiseks. Vooskeem koosneb erinevatest nooltega ühendatud kujunditest. Kujundid tähistavad erinevat tüüpi toiminguid ja nooled tähistavad nende toimingute sooritamise järjekorda.
Vooskeeme ja otsustuspuid kasutatakse sageli ka mitmesuguste tegevusjuhiste esitamiseks inimestele, näiteks hädaolukorra lahendamiseks vastavalt olukorra asjaoludele või selleks, et selgitada, kuidas mingeid plaane tuleks ellu viia.

Kolamid on dekoratiivsed mustrid, mida saab põrandale joonistada näiteks kriidiga. Kolami joonistamiseks märgitakse kõigepealt ära mõned punktid ja seejärel tõmmatakse nende ümber jooned. Iga joont alustatakse ja lõpetatakse samas punktis, joonistamise ajal kriiti üles ei tõsteta.
Joon võib ristuda teiste joonte või iseendaga, kuid ei tohi teise joonega kattuda või seda isegi puutuda ilma sellega ristumata. Iga joon peab olema joonistatud vähemalt ühe punkti ümber. Iga sellisel viisil joonistatud joont nimetatakse silmuseks.
Allpool illustreeritud kolamil on 6 silmust. Pange tähele, et silmused ristuvad erinevates kohtades ja musta värvi silmus ristub ka iseendaga.
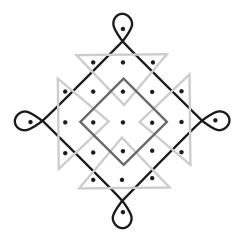
Millisel järgnevatest kolamitest on kõige vähem silmuseid?
[Raadionupud]
A. 
B. 
C. 
D. 
Õige vastus on: D.
Variandil A on 4 silmust:
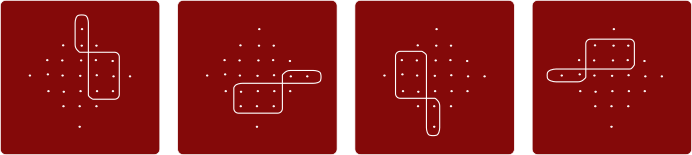
Variandil B on 5 silmust:

Variandil C on 3 silmust:
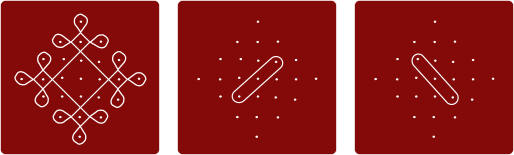
Variandil D on ainult üks silmus; ülevaatlikuse huvides näitame selle joonistamist etappide kaupa:

Kolamid on keerulised mustrid, mida leidub India linnades ja külades. Kuidas neid mustreid mäletatakse ja joonistatakse? Üks teooria on, et neid luuakse lihtsate reeglite järgi, mida antakse edasi põlvest põlve.
Reeglikogumite järgi neile vastavate tekstide genereerimist uuritakse arvutiteaduses formaalsete keelte teoorias. Kuigi genereerivad grammatikad mõeldi algselt välja tekstide (ühemõõtmeliste märgijadade) kirjeldamiseks, on hiljem seda ideed laiendatud ka mitmemõõtmelistele objektidele, sealhulgas ka graafilistele kujunditele. Selliseid meetodeid kasutatakse sageli ka generatiivses kunstis (ingl generative art).

Vaatame 6x5 ruudust koosnevat pilti, mille osad ruudud on mustad, osad valged:
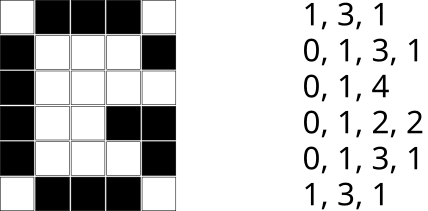
Selle pildi saab teisendada arvujadaks, lugedes iga rea puhul üle, mitu järjestikust ruutu on valged, seejärel mitu järjestikust ruutu on mustad, siis mitu järjestikust ruutu on valged jne, kuni jõuame rea lõppu. Pane tähele, et kui rida algab musta ruuduga, siis on selle rea alguses olevate valgete ruutude arv 0.
Lõpuks ühendame kõigi pildiridade kõik arvud ühte jadasse. Eeltoodud näites oleks tulemuseks selline jada: 1, 3, 1, 0, 1, 3, 1, 0, 1, 4, 0, 1, 2, 2, 0, 1, 3, 1, 1, 3, 1.
Milline 6x5 ruudust koosnev pilt oleks kujutatud jadaga 1, 4, 0, 1, 4, 1, 3, 1, 4, 1, 0, 1, 3, 1, 1, 3, 1?
[Raadionupud]
A. 
B. 
C. 
D. 
Õige vastus on: D.
Lahendamisel me saame järgida etteantud jada, joonistades selle järgi 6x5 maatriksi. Kui rida on täidetud, peame liikuma järgmisese ritta, alustades seal jälle valge värviga.
Alloleval pildil on näidatud õige vastus. Lisaks on näidatud, kuidas jada ridade kaupa tükkideks jagada.
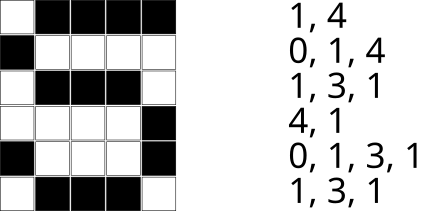
Variant A on vale, kuna selle jada oleks 0, 4, 1, 1, 1, 3, 1, 1, 3, 1, 1, 1, 2, 1, 1, 2, 1, 2, 2, 1.
Variant B on vale, kuna selle jada oleks 1, 4, 4, 1, 1, 3, 1, 0, 1, 4, 0, 1, 3, 1, 1, 3, 1.
Variant C on vale, kuna selle jada oleks 4, 1, 1, 2, 2, 0, 1, 2, 1, 1, 0, 1, 2, 1, 1, 0, 1, 2, 1, 1, 1, 2, 2.
Piltide salvestamiseks või edastamiseks elektroonikaseadmete vahel on vaja need arvudeks teisendada. Selleks on palju viise ja siin on toodud neist üks. Kasutades ühte arvu sama värvi ruutude jada esitamiseks, tihendab see meetod andmeid ehk vähendab andmete hulka ja see on informaatikas oluline. Seda meetodit saab täiustada mitmel viisil, näiteks lubades arvul viidata rohkem kui ühte rida hõlmavale ruutude jadale.
Andmete esitamise viiside leidmine on olnud väljakutse alates juba esimestest elektroonilistest seadmetest, sest sellega seotud valikud võivad mõjutada teabe töötlemiseks või saatmiseks ja vastuvõtmiseks kuluvat aega. Praegu on see probleem endiselt aktuaalne, eriti internetis: uute viiside loomine piltide, videote ja muude meediumifailide kodeerimiseks võib meie veebikasutamist kiirendada.
Selles ülesandes kirjeldatud meetodit kasutasid vanad faksiaparaadid dokumentide sisu edastamiseks.
Copyright © 2022 Bebras – International Challenge on Informatics and Computational Thinking.
Licensed under Creative Commons Attribution-ShareAlike 4.0 International License.
Flag icons by GoSquared.