
Вероника очень любит прыгать. Она нашла 17 квадратов, расположенных на одной линии, и составила из них план прохождения дорожки.
Вероника положила монету на один конец дорожки из квадратов, а сама встала на другой конец дорожки лицом к монете.

Она хочет прыгнуть на каждый квадрат дорожки, следуя этим правилам:
Какой из планов прохождения дорожки позволит ей добраться до монеты и при этом посетить все остальные квадраты?
[Raadionupud]
A. 
B. 
C. 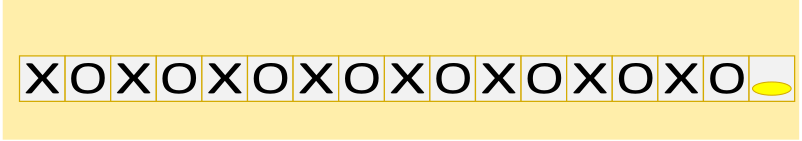
D. 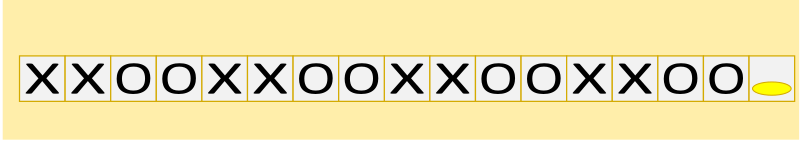
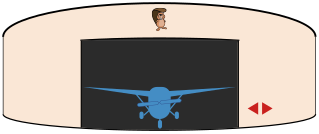
В аэропорту Бобруйска в круглом ангаре на вращающемся основании припарковано шесть самолётов. С помощью двух стрелок, расположенных на панели управления, основание можно поворачивать влево или вправо. Одним нажатием кнопки основание поворачивается точно на одно парковочное место либо влево, либо вправо, в соответствии с изображённой на кнопке стрелкой. Ворота ангара широки настолько, чтобы из них смог выехать только один самолёт. Основание вращается очень медленно, поэтому чем меньше будет нажатий кнопок, тем быстрее можно будет выполнить работу.
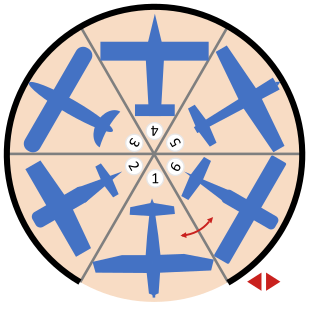
Утром, когда пилоты приезжают забирать самолеты, ворота всегда открыты именно напротив парковочного места №1. В лучшем случае необходимо нажать пять раз на кнопки со стрелкой, чтобы смогли выехать все самолёты. Это происходит, когда пилоты хотят попасть на парковочные места в порядке 1, 2, 3, 4, 5, 6 (для этого нужно пять раз подряд нажать кнопку со стрелкой вправо) или в порядке 1, 6, 5, 4, 3, 2 (для этого нужно пять раз подряд нажать кнопку со стрелкой влево).
Какой случай выезда самолётов будет наихудшим, т.е. какой порядок доступа к парковочным местам потребует наибольшего количества нажатий кнопок?
(Запишите шесть разных цифр, например, 654321. Если вариантов ответа несколько, то запишите любой из них.)
[Tekstikast]
На рисунке представлена карта горнолыжного курорта с лыжными трассами и подъёмниками:
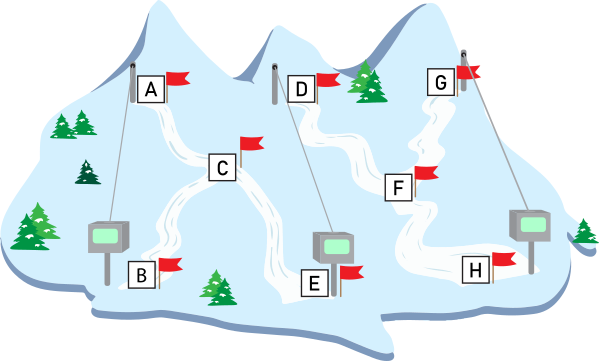
Лыжники могут подняться на гору только на подъёмниках, а спуск с горы возможен только на лыжах и по отмеченным на карте трассам. На курорте шесть горнолыжных трасс: A-C, C-B, C-E, D-F, F-H и G-F.
Бобр Виталик поспорил с другом, что он сможет проехать на лыжах так, что воспользуется каждым подъёмником и каждой лыжной трассой только по одному разу, не перемещаясь каким-либо другим образом.
Из какой точки должен стартовать Виталик, чтобы выиграть спор?
[Raadionupud]
A. Из точки A
B. Из точки B
C. Из точки C
D. Из точки D
E. Из точки E
F. Из точки F
G. Из точки G
H. Из точки H
Проживающее на шести островах сообщество туземцев хочет соединить острова, построив сеть подвесных мостов. Для этого был составлен план строительства возможных мостов. Числа показывают стоимость строительства каждого моста.
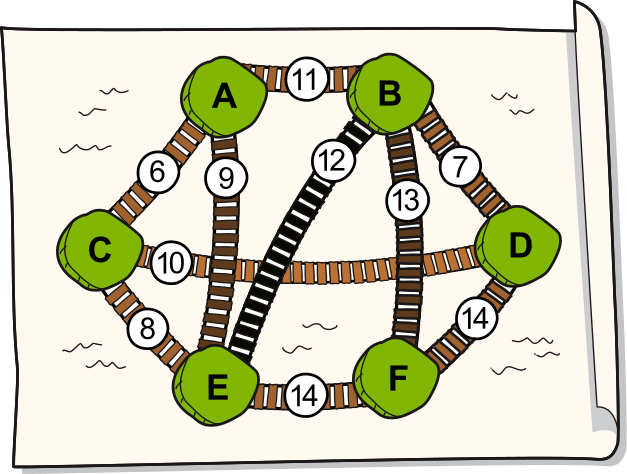
Сообщество хочет соединить острова таким образом, чтобы можно было перемещаться с каждого острова на любой другой остров (либо напрямую, либо через другие острова). В то же время сообщество хочет потратить на строительство мостов как можно меньше денег.
Изображённые на плане пересекающиеся мосты на самом деле будут находиться на разных высотах и перешагнуть над водой с одного моста на другой будет невозможно.
Какова будет минимальная стоимость строительства мостов, которые позволят соединить все шесть островов?
[Täisarv]
Два друга, Боб и Ральф, играют в игру. Сначала внизу листа они рисуют чёрную линию и называют её «землёй». Затем они рисуют несколько синих и красных линий, создавая фигуру мышонка:
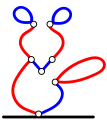
Правила игры следующие:
Ниже приведена одна из возможных последовательностей ходов. Для каждого хода есть два рисунка: на первом рисунке серым цветом отмечена линия, которую игрок намерен удалить, а второй рисунок показывает результат этого удаления.
Ход Боба:
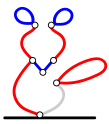
Ход Ральфа:
Ход Боба:
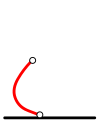
Ход Ральфа:


Поскольку у Боба больше нет линий, которые он мог бы удалить, то он проигрывает игру, и Ральф становится победителем.
Пронумеруем синие линии следующим образом:
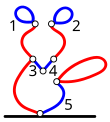
Какую линию Боб должен удалить первой, чтобы быть уверенным в своей победе, даже если Ральф каждый раз будет делать лучший из своих возможных ходов?
[Raadionupud]
A. Линию 1
B. Линию 2
C. Линию 3
D. Линию 4
E. Линию 5
F. У Боба нет возможности выиграть
Бобр Марк нашёл два хороших места, где можно организовать тайники с запасами еды. На карте он хочет отметить эти места крестиками, чтобы не забыть их расположение. Но если его соперница Кэт найдёт карту, то она будет знать, где находятся тайники!
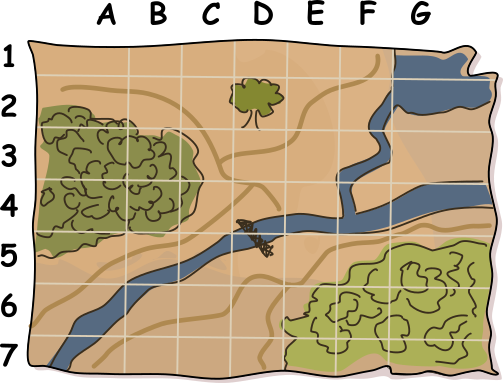
Чтобы запутать Кэт, Марк добавил несколько случайных крестиков в другие квадраты карты, следя за тем, чтобы общее количество крестиков в каждой строке и столбце всегда было чётным (напомним, что 0 также является чётным числом). Затем он стёр два крестика, которые указывали на расположение его тайников. Готовая карта выглядит так:
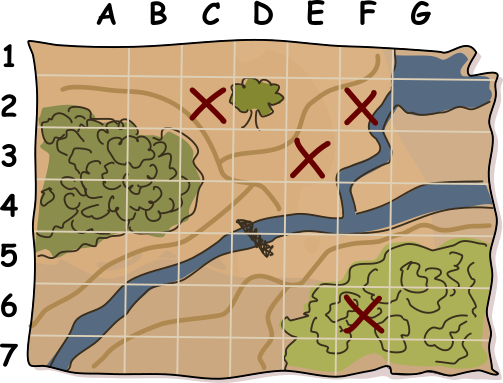
В каких квадратах находятся запасы еды Марка?
(Запишите обозначения двух квадратов, например, A1 B2.)
[Tekstikast]
На каждой вершине восьмиугольника записаны три или четыре буквы. Исходящая из центра восьмиугольника чёрная стрелка указывает на некоторую группу букв. Стрелка может вращаться только по движению часовой стрелки.
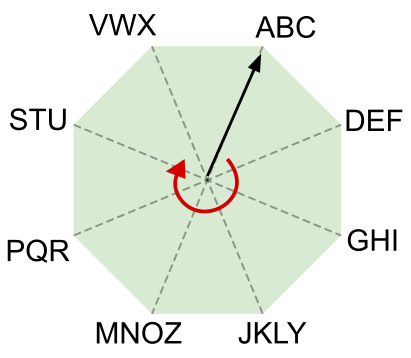
Воспользуемся этими восьмиугольником и стрелкой для кодирования сообщений. В начале кодирования нового сообщения стрелка указывает на группу букв ABC. Далее кодируем каждую букву сообщения следующим образом:
Например, сообщение "TREE" будет закодировано с помощью последовательности 62-73-42-02.
Как будет закодировано сообщение "WATER"?
[Raadionupud]
A. 72-11-26-32-53
B. 62-11-62-22-43
C. 62-11-26-22-53
D. 72-11-62-32-43
В классе имеется 31 стул. Они расположены по кругу и пронумерованы от 1 до 31, как показано на рисунке.
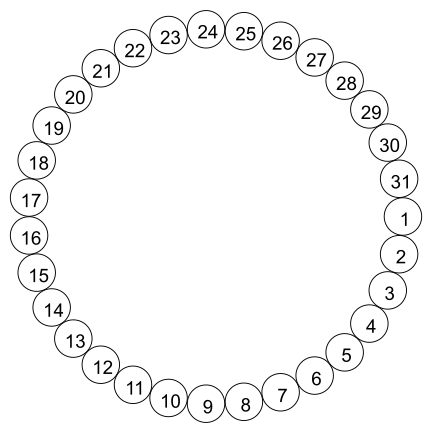
Дети играют в игру по следующим правилам:
Допустим, что Катя и Маша — близнецы, родившиеся 20 апреля, Тимур родился 21 января, а Толя — 22 сентября.
Дети заходят в класс в следующем порядке: Катя, Маша, Толя, Тимур. Катя садится на 20ый стул, Маша на 21ый стул, Толя на 22ой стул, а Тимур на 23ий стул.
Если же дети заходят в класс в порядке Маша, Тимур, Толя, Катя, то Маша садится на 20ый стул, Тимур на 21ый стул, Толя на 22ой стул, а Катя на 23ий стул.
Шестеро учеников уже вошли в класс, и они сидят, как показано в таблице:
| Имя | День рождения | Номер стула |
|---|---|---|
| Аня | 11 мая | 13 |
| Боря | 12 февраля | 12 |
| Веня | 14 сентября | 14 |
| Гена | 11 августа | 11 |
| Диана | 13 апреля | 15 |
| Елена | 12 июля | 16 |
Какое из следующих утверждений не может быть верным?
[Raadionupud]
A. Веня сел первым
B. Елена села последней
C. Диана села раньше Ани
D. Боря сел раньше Гены
Аня, Боря, Вера и Гена решили приготовить большой завтрак. Они пошли в магазин, чтобы купить четыре продукта: яйца, сосиски, бобы и помидоры.
Всего они купили восемь товаров: две коробки яиц, две упаковки сосисок, две банки бобов и два помидора.
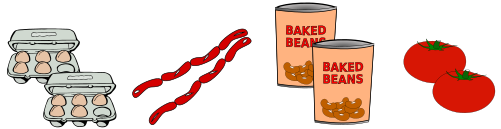
Каждый из них купил по два разных продукт питания, и при этом известно, что:
Если Аня и Гена купили один и тот же продукт питания, то что это за продукт?
[Raadionupud]
A. Коробка яиц
B. Упаковка сосисок
C. Банка бобов
D. Помидор
Четыре элемента должны быть размещены в квадрате 2x2 так, чтобы элементы касались друг друга только сторонами с одинаковыми символами. Один из возможных способов таков:
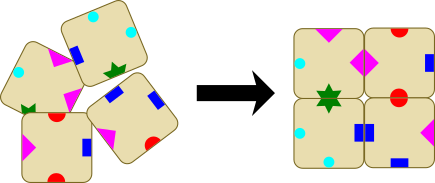
Теперь у нас имеется пять элементов.

Из этих пяти элементов нужно выбрать четыре и разместить их, следуя описанному выше правилу. В этом случае есть только один вариант для выбора подходящих четырёх элементов.
Какой элемент в данном случае не будет использован?
[Raadionupud]
A. Элемент A
B. Элемент B
C. Элемент C
D. Элемент D
E. Элемент E
Бобр Марк ищет номер телефона своего друга на очень длинной интернет-странице. Марк не уверен, как точно пишется имя друга, поэтому использует для поиска специальные символы:
| Символ | Значение |
|---|---|
| ? | точно одна неизвестная буква |
| & | точно две неизвестные буквы подряд |
| % | любое количество неизвестных букв до конца имени |
Например, поисковый запрос «Ma%» может выдать имена Maрия, Maрк и т.д.
Какие из следующих имён выдаст поисковый запрос «S?rah B&cht%»?
(Отметьте все правильные ответы.)
[Märkeruudud]
A. Sarah Birchtree
B. Sara Benchton
C. Sarah Bilchman
D. Sirah Beachtram
У бобра Максима в электронной таблице есть данные и формулы.

Теперь на основании вычисленных по формулам значений (в строке 3) он строит диаграммы.
Какую из приведенных ниже диаграмм Максим никогда не получит на основании этих данных?
[Raadionupud]
A. 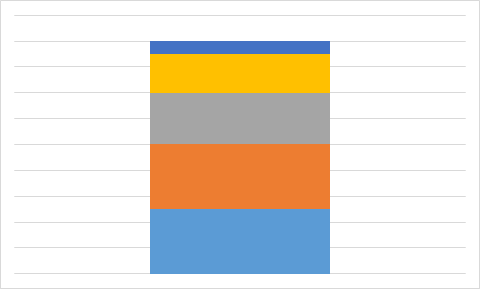
B. 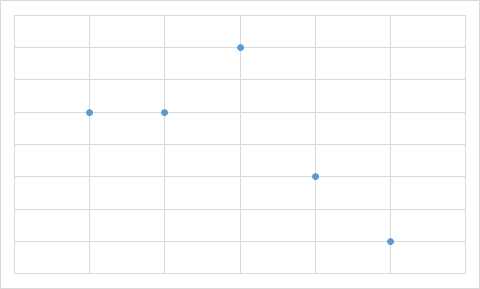
C. 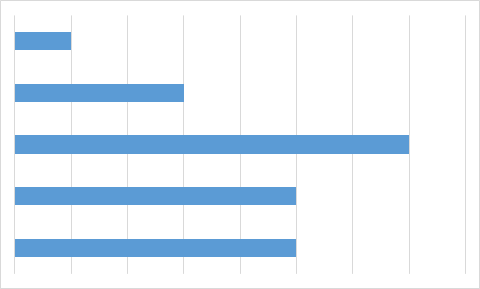
D. 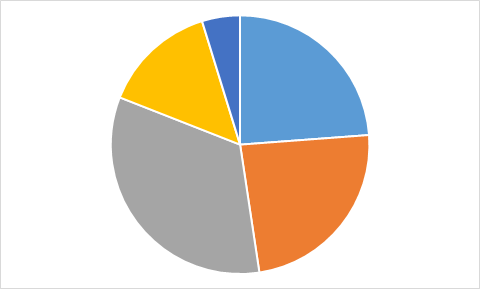
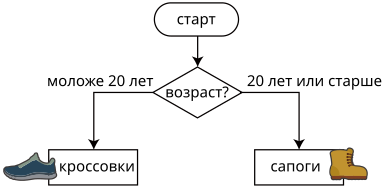
Интернет-магазин одежды использует систему рекомендаций, которая базируется на персональных данных покупателей. Например, если клиент хочет купить обувь, то программа следует приведённым ниже правилам и рекомендует купить сапоги:
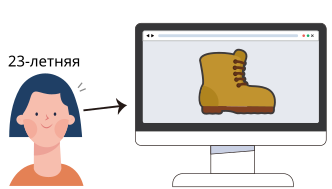
Однажды часть правил, на которых основывались рекомендации по одежде, были случайно удалены. На нижеприведённом рисунке показана оставшаяся часть правил.

К счастью, некоторые ранее данные рекомендации сохранились:
| Клиент | Рекомендация | |
|---|---|---|
| 18-летняя 140 см |
Однотонная юбка |  |
| 32-летняя 145 см |
Пёстрая юбка |  |
| 28-летний 155 см |
Пёстрые штаны |  |
| 15-летний 160 см |
Однотонные штаны |  |
| 10-летняя 152 см |
Однотонные штаны |  |
Основываясь на вышеприведённой информации, какой может быть недостающая часть рисунка?
[Raadionupud]
A. 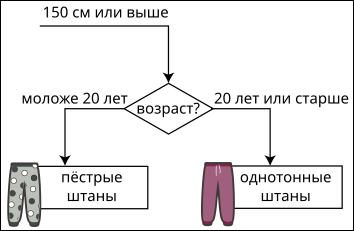
B. 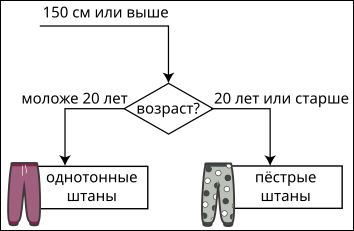
C. 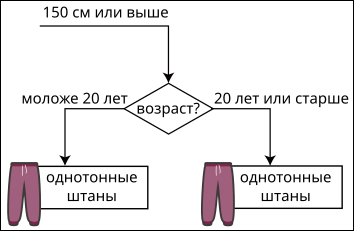
D. 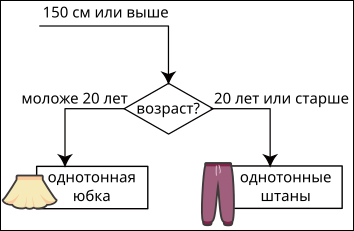
Коламы — это декоративные узоры, которые можно нарисовать на полу, например, с помощью мела. Чтобы нарисовать колам, сначала отмечают несколько точек, а затем рисуют вокруг них линии. Каждая линия начинается и заканчивается в одной и той же точке, мел во время рисовании не отрывается от пола.
Линия может пересекать другие линии или саму себя, но не может совпадать или даже касаться другой линии, не пересекая её. Каждая линия должна быть нарисована вокруг хотя бы одной точки. Каждая линия, нарисованная таким образом, называется петлей.
Колам, показанный ниже, имеет 6 петель. Обратите внимание, что петли пересекаются в разных местах, а петля чёрного цвета также пересекает саму себя.
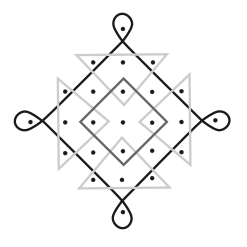
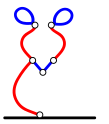
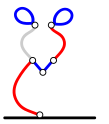
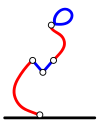
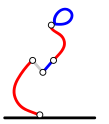
Какой из следующих коламов имеет наименьшее количество петель?
[Raadionupud]
A. 
B. 
C. 
D. 
Рассмотрим изображение, состоящее из 6x5 квадратов, где некоторые квадраты чёрные, а некоторые — белые:
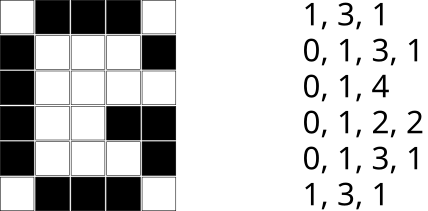
Это изображение можно преобразовать в последовательность чисел, подсчитав для каждой строки, сколько квадратов последовательно окрашено в белый цвет, а затем сколько квадратов последовательно окрашено в чёрный цвет, далее сколько квадратов последовательно окрашено в белый цвет и т.д., пока мы не достигнем конца строки. Обратите внимание, что если строка начинается с чёрного квадрата, то количество белых квадратов в начале этой строки равно 0.
В самом конце мы должны объединить все числа, которые получились для каждой строчки, в одну последовательность чисел. В случае вышеприведённого изображения получится следующая последовательность: 1, 3, 1, 0, 1, 3, 1, 0, 1, 4, 0, 1, 2, 2, 0, 1, 3, 1, 1, 3, 1.
Kакое изображение, состоящее из 6x5 квадратов, будет представлено последовательностью 1, 4, 0, 1, 4, 1, 3, 1, 4, 1, 0, 1, 3, 1, 1, 3, 1?
[Raadionupud]
A. 
B. 
C. 
D. 