

Вероника очень любит прыгать. Она нашла 17 квадратов, расположенных на одной линии, и составила из них план прохождения дорожки.
Вероника положила монету на один конец дорожки из квадратов, а сама встала на другой конец дорожки лицом к монете.

Она хочет прыгнуть на каждый квадрат дорожки, следуя этим правилам:
Какой из планов прохождения дорожки позволит ей добраться до монеты и при этом посетить все остальные квадраты?
[Raadionupud]
A. 
B. 
C. 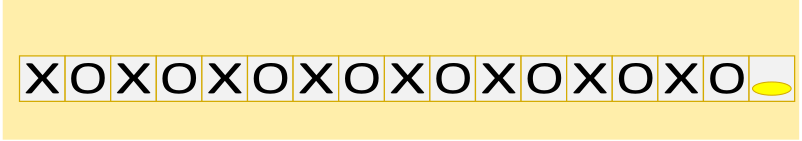
D. 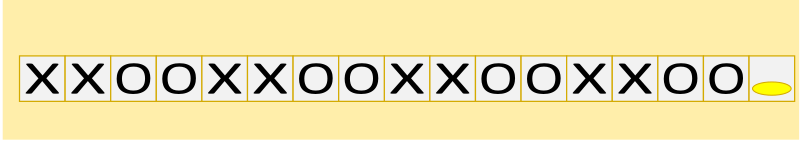
Правильный ответ: D.
Порядок прыжков отмечен стрелками.
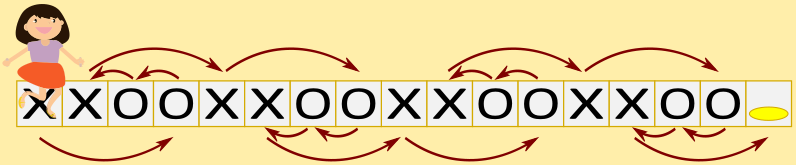
Варианты А и B неверны, так как девочка пропустит квадрат с монетой в конце дорожки, а также второй и третий квадраты слева. Вариант C неверен, потому что она пропустит второй квадрат слева.
Нахождение последовательности действий для достижения цели по заранее заданным правилам называется алгоритмизацией. Робот или компьютерное приложение можно запрограммировать на работу в соответствии с заранее определёнными правилами. Если в результате нам нужен конкретный выход, то мы должны также указать соответствующий ввод. Допустим, у нас есть длинный узкий коридор в форме буквы L, и наш робот-пылесос может передвигаться только прямо и поворачивать на 90° вправо. Следовательно, нам нужно поставить его в конце более короткой части буквы L, иначе робот не сможет пропылесосить весь коридор.

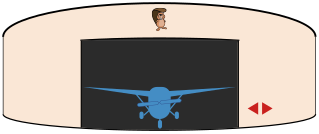
В аэропорту Бобруйска в круглом ангаре на вращающемся основании припарковано шесть самолётов. С помощью двух стрелок, расположенных на панели управления, основание можно поворачивать влево или вправо. Одним нажатием кнопки основание поворачивается точно на одно парковочное место либо влево, либо вправо, в соответствии с изображённой на кнопке стрелкой. Ворота ангара широки настолько, чтобы из них смог выехать только один самолёт. Основание вращается очень медленно, поэтому чем меньше будет нажатий кнопок, тем быстрее можно будет выполнить работу.
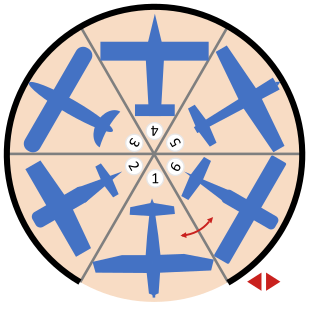
Утром, когда пилоты приезжают забирать самолеты, ворота всегда открыты именно напротив парковочного места №1. В лучшем случае необходимо нажать пять раз на кнопки со стрелкой, чтобы смогли выехать все самолёты. Это происходит, когда пилоты хотят попасть на парковочные места в порядке 1, 2, 3, 4, 5, 6 (для этого нужно пять раз подряд нажать кнопку со стрелкой вправо) или в порядке 1, 6, 5, 4, 3, 2 (для этого нужно пять раз подряд нажать кнопку со стрелкой влево).
Какой случай выезда самолётов будет наихудшим, т.е. какой порядок доступа к парковочным местам потребует наибольшего количества нажатий кнопок?
(Запишите шесть разных цифр, например, 654321. Если вариантов ответа несколько, то запишите любой из них.)
[Tekstikast]
Правильный ответ: 413625 или 415263.
Имеется два наихудших случая: 4, 1, 3, 6, 2, 5 и 4, 1, 5, 2, 6, 3.
Наихудший случай, а значит и правильный ответ, можно найти, если следующим всегда выбирать непустое парковочное место, находящееся дальше всех от ворот. Здесь необходимо представлять себе результат каждого поворота и то, как основание шаг за шагом, место за местом, будет пустеть. Поскольку основание можно вращать в обоих направлениях, то существует более одного решения.
4, 1, 3, 6, 2, 5:
4, 1, 5, 2, 6, 3:
Можно заметить, что в случае одного или двух самолётов имеется только одно решение. Далее, в случае чётного числа самолётов всегда имеется два решения; в случае же нечётного числа самолётов — четыре решения. Хороший вопрос для размышления: почему же это так?
Преимущество круглого ангара в том, что он позволяет сэкономить место. А как насчёт времени? Если самолёты припаркованы в том же порядке, в котором приезжают пилоты, то пилоты могут быстро сесть в самолёт и взлететь. Это было бы наилучшим вариантом для получения самолёта, но как продемонстрировало это задание, для большинства процессов существуют и наихудшие варианты. В худшем случае время будет потеряно, поэтому придётся решить, что важнее: экономия места или времени.
В информатике очень важна оценка эффективности процессов. Хотя знать наилучшие варианты для решения проблемы тоже хорошо, именно знание наихудшего из возможных решений является наиболее важной характеристикой эффективности решения. Эффективность означает, что ресурсы, такие как время, энергия и пространство для хранения, используются бережно.
Сегодня примером эффективного хранения может быть бизнес почтовых заказов: часто для более быстрого доступа к товарам их не сортируют ни по алфавиту, ни по артикулам, а вместо этого при размещении товаров учитывается, как часто их обычно покупают.

На рисунке представлена карта горнолыжного курорта с лыжными трассами и подъёмниками:
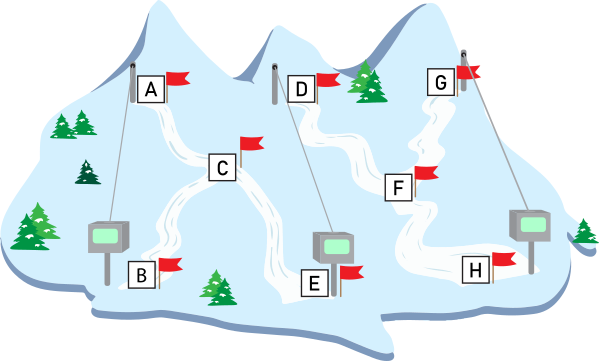
Лыжники могут подняться на гору только на подъёмниках, а спуск с горы возможен только на лыжах и по отмеченным на карте трассам. На курорте шесть горнолыжных трасс: A-C, C-B, C-E, D-F, F-H и G-F.
Бобр Виталик поспорил с другом, что он сможет проехать на лыжах так, что воспользуется каждым подъёмником и каждой лыжной трассой только по одному разу, не перемещаясь каким-либо другим образом.
Из какой точки должен стартовать Виталик, чтобы выиграть спор?
[Raadionupud]
A. Из точки A
B. Из точки B
C. Из точки C
D. Из точки D
E. Из точки E
F. Из точки F
G. Из точки G
H. Из точки H
Правильный ответ: C (из точки C).
Чтобы спуститься со всех горнолыжных трасс только по одному разу и воспользоваться каждым подъёмником только по одному разу, необходимо пройти точки в следующем порядке: C, B, A, C, E, D, F, H, G, F.
На нижеприведённом рисунке показаны подъёмники и трассы, а также направление движения Виталика:
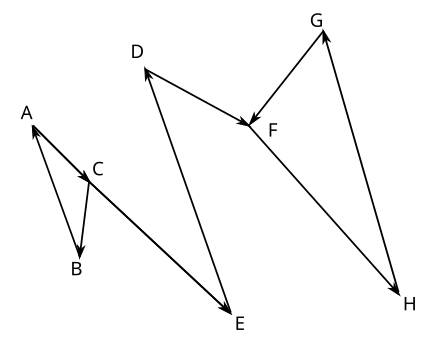
На рисунке видно, что для каждой точки, кроме C и F, имеется только одна входящая и одна исходящая трасса. Точка C имеет две исходящих трассы (в направлении точек B и E), а точка F имеет две входящих трассы (из точек D и G). Это означает, что решение должно обязательно начинаться в точке C и заканчиваться в точке F.
Если начать движение из точки C в направлении точки E, то после этого уже невозможно будет попасть в точки A и B. Таким образом, единственное возможное решение — это начать движение из точки C в направлении точки B. Тогда на каждом последующем шаге всегда будет одна неиспользованная трасса или подъёмник, чтобы продолжить движение вперёд.
Использованный в объяснении правильного ответа рисунок называется графом (англ graph). Граф имеет вершины (точки, обозначенные на рисунке флажками) и рёбра (линии, обозначающие на рисунке трассы и подъёмники). В этом задании мы имеем дело с ориентированным графом (англ directed graph, digraph), поскольку важно знать, в каком направлении можно двигаться из одной вершины в другую; на разрешённое направление указывают имеющиеся на концах рёбер стрелки.
Графы довольно часто используются в информатике для представления задачи в абстрактной виде. Как видим, такой граф может содержать достаточно информации для решения задания.

Проживающее на шести островах сообщество туземцев хочет соединить острова, построив сеть подвесных мостов. Для этого был составлен план строительства возможных мостов. Числа показывают стоимость строительства каждого моста.
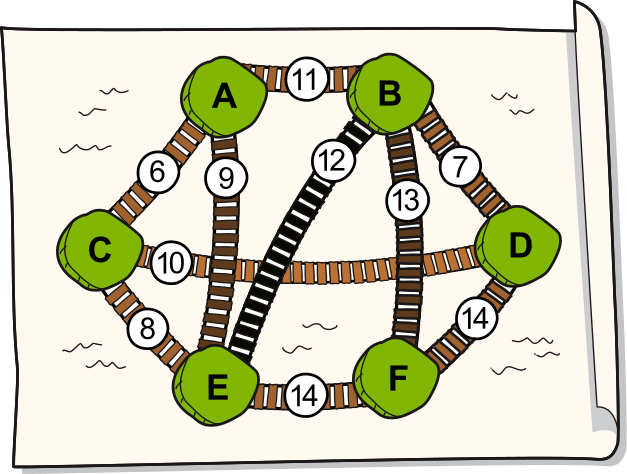
Сообщество хочет соединить острова таким образом, чтобы можно было перемещаться с каждого острова на любой другой остров (либо напрямую, либо через другие острова). В то же время сообщество хочет потратить на строительство мостов как можно меньше денег.
Изображённые на плане пересекающиеся мосты на самом деле будут находиться на разных высотах и перешагнуть над водой с одного моста на другой будет невозможно.
Какова будет минимальная стоимость строительства мостов, которые позволят соединить все шесть островов?
[Täisarv]
Правильный ответ: 44.
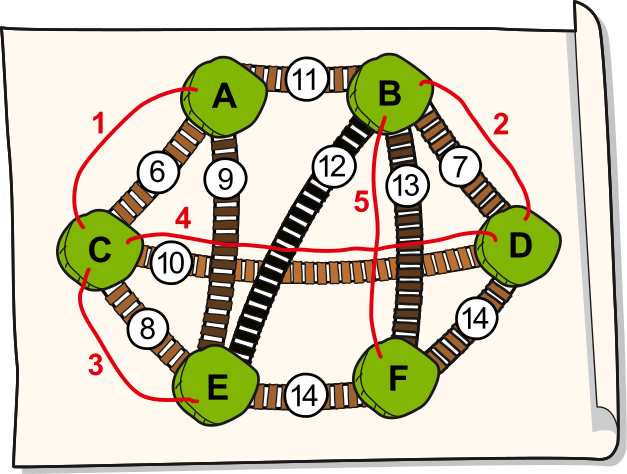
Теперь у нас соединены все шесть островов, а общая стоимость построенных для этого мостов составит 6+7+8+10+13=44.
Но откуда мы знаем, что это самый дешёвый вариант?
Во-первых, отметим, что для соединения шести островов обязательно потребуется пять мостов. Каждый новый мост соединяет два объекта в один, т.е. уменьшает количество объектов на единицу. В начале каждый остров представляет собой отдельный объект, а в конце все они объединены в один единственный объект. Значит, количество объектов уменьшилось на пять, и для этого нам потребовалось пять мостов.
Во-вторых, о каждом непостроенном мосте мы можем рассуждать следующим образом: если бы мы построили этот мост, то мы могли бы оставить непостроенным один из оставшихся мостов, с которым новый мост образовывал бы круг; но таким образом мы бы заменили более дешевый мост на более дорогой, а это, соответственно, привело бы к пропорциональному увеличению суммы за строительство всех мостов.
Таким образом, можно с уверенностью сказать, что вышеупомянутый жадный алгоритм (англ greedy algorithm) определенно обеспечит наилучшее возможное решение этого задания.
С точки зрения информатики это задание на нахождение в графе остовного дерева с минимальным весом. Граф (англ. graph) — это структура, состоящая из вершин (в случае нашего задания — это острова) и соединяющих их рёбер (в случае нашей задачи — это мосты). Один граф называется подграфом другого, если он может быть получен из другого графа путём удаления некоторого числа рёбер и вершин (в этом случае рёбра можно удалять в отдельности, но при удалении вершины вместе с ней всегда удаляются все соединенные с ней рёбра).
Остовное дерево графа (англ spanning tree) — это подграф, в котором остались все вершины и такое количество рёбер, при котором из каждой вершины существует только один путь к любой другой вершине. Весом остовного дерева графа называется сумма весов оставшихся рёбер (в нашем задании — это стоимость постройки мостов).
Существует несколько известных методов нахождения остовного дерева графа. Описанный выше алгоритм (мы добавляем рёбра в порядке возрастания их веса, опуская только те, которые вызывают цикл) известен как алгоритм Краскала (англ Kruskal's algorithm).

Два друга, Боб и Ральф, играют в игру. Сначала внизу листа они рисуют чёрную линию и называют её «землёй». Затем они рисуют несколько синих и красных линий, создавая фигуру мышонка:
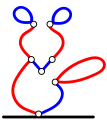
Правила игры следующие:
Ниже приведена одна из возможных последовательностей ходов. Для каждого хода есть два рисунка: на первом рисунке серым цветом отмечена линия, которую игрок намерен удалить, а второй рисунок показывает результат этого удаления.
Ход Боба:
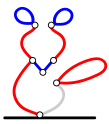
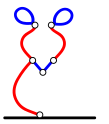
Ход Ральфа:
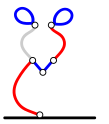
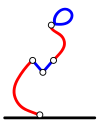
Ход Боба:
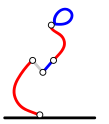
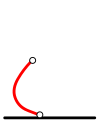
Ход Ральфа:


Поскольку у Боба больше нет линий, которые он мог бы удалить, то он проигрывает игру, и Ральф становится победителем.
Пронумеруем синие линии следующим образом:
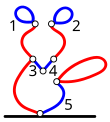
Какую линию Боб должен удалить первой, чтобы быть уверенным в своей победе, даже если Ральф каждый раз будет делать лучший из своих возможных ходов?
[Raadionupud]
A. Линию 1
B. Линию 2
C. Линию 3
D. Линию 4
E. Линию 5
F. У Боба нет возможности выиграть
Правильный ответ: B (линию 2).
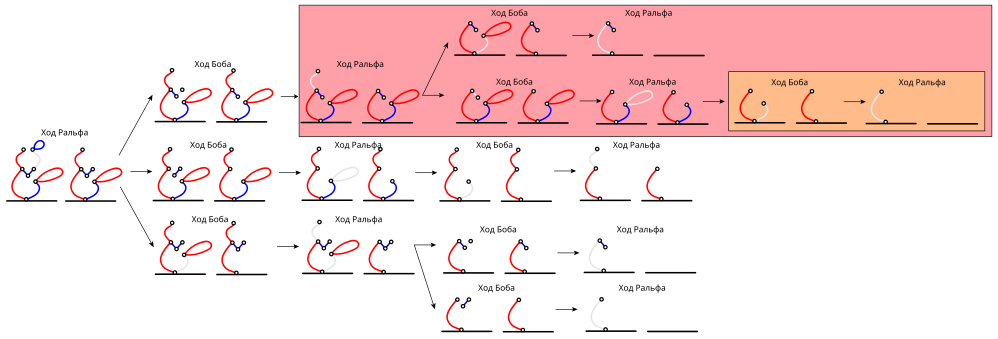
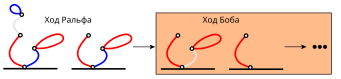
Чтобы доказать, что удаление линии 2 гарантирует Бобу победу, давайте сначала выберем один из возможных ответов Ральфа на этот первоначальный ход. Далее полностью проиграем игры, пока не найдём выигрышную последовательность (или стратегию). Нижеприведённый рисунок демонстрирует выигрышную стратегию, если Ральф удалит левую сторону «лица»:

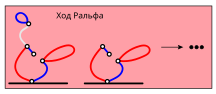
Чтобы избежать игры вслепую, Бобу выгодно направить игру Ральфа в русло, которое присутствует в вышеприведённой выигрышной стратегии. Это позволит Бобу обеспечить себе победу, используя ту же последовательность ходов, что и в вышеприведённой стратегии. На последующих рисунках эти ситуации отмечены прямоугольниками разных цветов, чтобы проиллюстрировать, как вышеупомянутая стратегия может быть применена к оставшимся ответам Ральфа на первоначальный ход Боба:
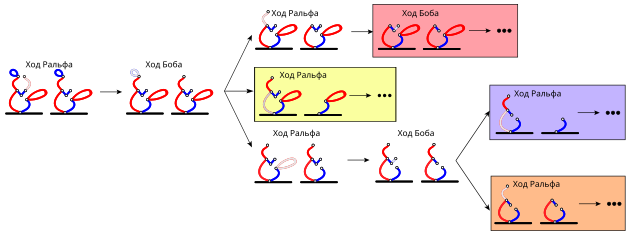
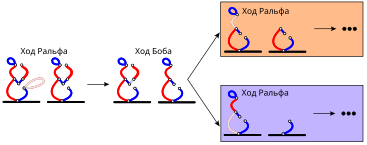
Для полноты понимания ситуации можно также показать, что у Боба нет шансов на победу, если он начнёт с удаления какой-то другой линии, а Ральф на каждом ходу выберет для себя идеальный ответ:
Представленная в этом задании игра (также известная как Хакенбуш, https://en.wikipedia.org/wiki/Hackenbush) относится к так называемым комбинаторным играм. Это игры для двух игроков, которые отвечают трём критериям:
Популярными примерами таких игр являются шахматы, шашки, го и крестики-нолики.
Комбинаторные игры являются очень ценными объектами исследования информатики (особенно теоретической информатики и искусственного интеллекта). Области интересов включают определение победителя, когда обе стороны всегда делают наилучший возможный ход (так называемая идеальная игра), поиск максимизирующих шансы на победу стратегий, и эвристики для оценки того, какой игрок имеет преимущество в данном состоянии.
Для анализа таких игр можно использовать так называемые игровые деревья (англ game tree), описывающие все возможные позиции и возможные ходы в каждой позиции. Однако игры могут иметь очень большое количество возможных позиций, а это делает создание всего дерева игры неэффективным или даже невозможным. Чтобы справиться с этим, были разработаны алгоритмы, которые избегают многократного исследования одних и тех же позиций (как мы сделали в нашем решении) или «обрезают» игровое дерево, чтобы не исследовать дальше позиции, оценка которых хуже некоторого порога. Искусственный интеллект обучается с помощью таких методов, как обучение с подкреплением (англ reinforcement learning), когда компьютер обучается, «учась на своих ошибках», и таким образом улучшает процесс принятия решений в сложных играх, таких как шахматы и го.

Бобр Марк нашёл два хороших места, где можно организовать тайники с запасами еды. На карте он хочет отметить эти места крестиками, чтобы не забыть их расположение. Но если его соперница Кэт найдёт карту, то она будет знать, где находятся тайники!
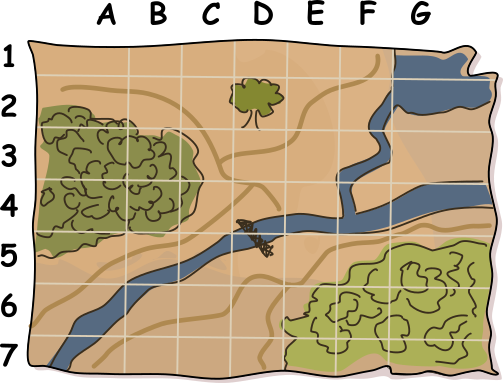
Чтобы запутать Кэт, Марк добавил несколько случайных крестиков в другие квадраты карты, следя за тем, чтобы общее количество крестиков в каждой строке и столбце всегда было чётным (напомним, что 0 также является чётным числом). Затем он стёр два крестика, которые указывали на расположение его тайников. Готовая карта выглядит так:
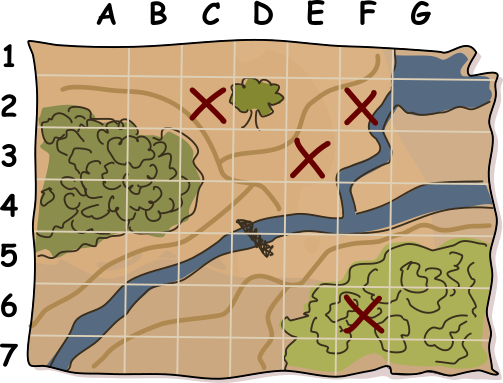
В каких квадратах находятся запасы еды Марка?
(Запишите обозначения двух квадратов, например, A1 B2.)
[Tekstikast]
Правильный ответ: C3 E6.
Вот расположение двух тайников:
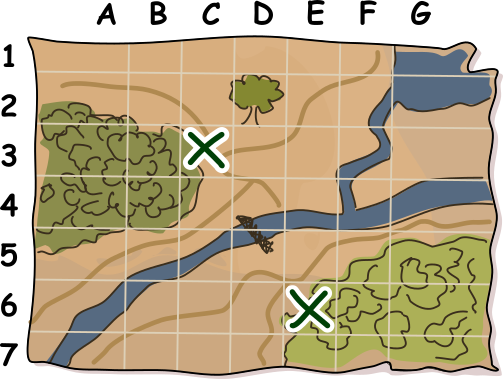
Чтобы их найти, посмотрим на итоговую карту. Мы заметим, что на ней имеется две строки и два столбца, где количество крестиков нечётное — это строки 3 и 6, а также столбцы C и E. На следующем рисунке эти строки и столбцы отмечены жёлтым цветом:
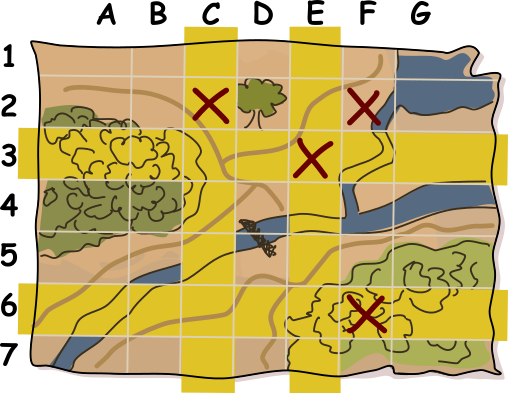
Значит, два удалённых крестика должны быть в этих строках и столбцах. Далее мы должны найти способ добавить крестики обратно так, чтобы восстановить свойство чётности.
Имеется четыре места пересечения жёлтых строк и столбцов. Верхний правый (E3) уже отмечен крестиком, но это не может быть обозначением тайника, потому что мы знаем, что Марк стёр указывающие на настоящие тайники крестики. Итак, чтобы восстановить чётное количество крестиков в строке 3, нам нужно добавить крестик в верхний левый квадрат пересечения, т.е. в квадрат С3. Теперь мы знаем расположение одного тайника.
Крестик, обозначающий второй тайник, не может находиться в нижнем левом квадрате пересечения, т.е. в квадрате C6, потому что в результате мы бы получили 3 крестика в столбце C, а 3 — это нечётное число. Следовательно, единственный выбор — это нижний правый квадрат пересечения, т.е. квадрат E6. Вот так мы и получили приведенный выше ответ.
Вот карта, какой она была до удаления крестиков, и действительно в каждой строке и в каждом столбце чётное количество крестиков:
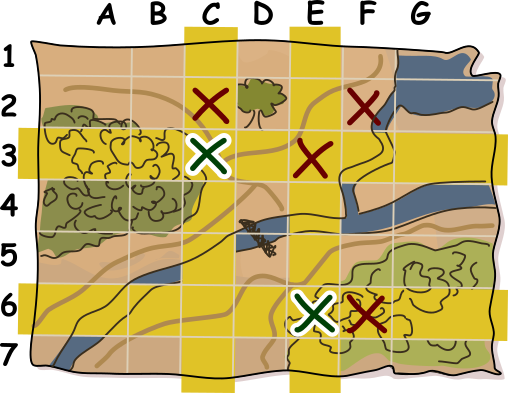
В этом задании Марк применил часто используемую в информатике технику, связанную с концепцией бита чётности. Это часть более широкого набора приёмов, известных как методы обнаружения и исправления ошибок. Идея заключается в том, что когда нам нужно сохранить или передать данные в виде последовательности битов (единиц и нулей), то к последовательности мы добавляем дополнительные биты. Эти дополнительные биты помогают нам определить, возникли ли ошибки при передаче или сохранении данных, например, когда отправили 1, а получили 0.
Если мы используем простой код обнаружения ошибок, то мы можем добавить бит чётности, чтобы количество единиц было чётным. Например, к последовательности "0110101" мы добавляем ноль и получаем новую последовательность «01101010», где количество единиц остаётся чётным. Если, например, второй бит был бы получен неправильно, т.е. получили бы последовательность «00101010», то полученное сообщение не удовлетворяло бы нашему требованию чётности (в последовательности имеется нечётное количество единиц). Заметим, что если ошибочных битов больше одного, то такой простой метод может и не обнаружить проблему.

На каждой вершине восьмиугольника записаны три или четыре буквы. Исходящая из центра восьмиугольника чёрная стрелка указывает на некоторую группу букв. Стрелка может вращаться только по движению часовой стрелки.
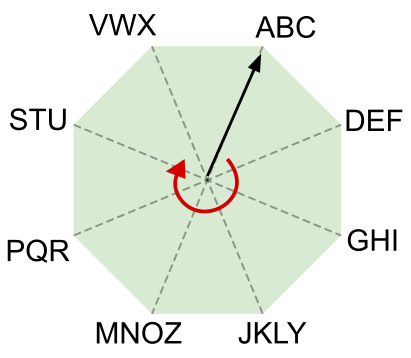
Воспользуемся этими восьмиугольником и стрелкой для кодирования сообщений. В начале кодирования нового сообщения стрелка указывает на группу букв ABC. Далее кодируем каждую букву сообщения следующим образом:
Например, сообщение "TREE" будет закодировано с помощью последовательности 62-73-42-02.
Как будет закодировано сообщение "WATER"?
[Raadionupud]
A. 72-11-26-32-53
B. 62-11-62-22-43
C. 62-11-26-22-53
D. 72-11-62-32-43
Правильный ответ: D (72-11-62-32-43).
Мы получим правильный ответ, если закодируем сообщение "WATER" по буквам. Код сообщения содержит 5 пар цифр:
Таким образом, код сообщения 72-11-62-32-43.
Одним из методов защиты данных от посторонних лиц является шифрование. Наука о шифрах или криптография (англ cryptography) появилась уже 3500 лет назад. Один из самых простых шифров — это замена каждой буквы на другую букву. Такой т.н. шифр подстановки (англ substitution cipher) легко взломать, потому что частотность разных букв в каждом языке своя, и на основе этой частотности можно довольно легко найти коды наиболее часто используемых букв.
В нашем задании используется метод, который за счёт вращения стрелки даёт разные коды для одной и той же буквы — в зависимости от того, какая буква была предыдущей в сообщении. Благодаря этому создаётся некоторая изменчивость, вариативность, в шифре и это затрудняет его взлом. Однако шифр достаточно прост, чтобы его можно было легко запомнить.
Если бы мы разделили буквы на группы по-другому или расположили группы в вершинах восьмиугольника в другом порядке, то мы бы получили разные коды для одного и того же сообщения. Такая настройка схемы шифрования называется ключом шифрования (англ encryption key), а его угадывание — криптоанализом (англ cryptoanalysis).

В классе имеется 31 стул. Они расположены по кругу и пронумерованы от 1 до 31, как показано на рисунке.
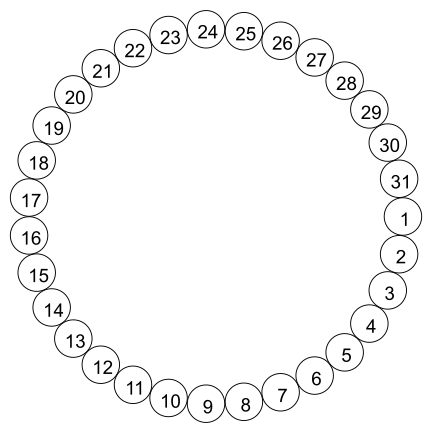
Дети играют в игру по следующим правилам:
Допустим, что Катя и Маша — близнецы, родившиеся 20 апреля, Тимур родился 21 января, а Толя — 22 сентября.
Дети заходят в класс в следующем порядке: Катя, Маша, Толя, Тимур. Катя садится на 20ый стул, Маша на 21ый стул, Толя на 22ой стул, а Тимур на 23ий стул.
Если же дети заходят в класс в порядке Маша, Тимур, Толя, Катя, то Маша садится на 20ый стул, Тимур на 21ый стул, Толя на 22ой стул, а Катя на 23ий стул.
Шестеро учеников уже вошли в класс, и они сидят, как показано в таблице:
| Имя | День рождения | Номер стула |
|---|---|---|
| Аня | 11 мая | 13 |
| Боря | 12 февраля | 12 |
| Веня | 14 сентября | 14 |
| Гена | 11 августа | 11 |
| Диана | 13 апреля | 15 |
| Елена | 12 июля | 16 |
Какое из следующих утверждений не может быть верным?
[Raadionupud]
A. Веня сел первым
B. Елена села последней
C. Диана села раньше Ани
D. Боря сел раньше Гены
Правильный ответ: C (Диана села раньше Ани).
Веня сидит на стуле, номер которого соответствует дню его рождения. Значит, он мог зайти в класс первым, а вариант А может быть верным утверждением.
Чтобы сесть на стул под номером 16, Елена должна была зайти в класс после тех, кто уже сидит на стульях 12–15. Гена сидит на стуле 11, а это значит, что он должен был зайти раньше Ани, с которой у него один и тот же день рождения. Следовательно, вариант B — это верное утверждение.
Если бы Диана зашла раньше Ани, то стул под номером 13 был бы свободен, и Диане не пришлось бы садиться на стул под номером 15. Следовательно, вариант С не может быть верным утверждением.
Боря и Гена, оба сидят на стульях, номера которых соответствуют дням их рождения, и они могли зайти в класс всё равно в каком порядке. Таким образом, вариант D может быть верным утверждением.
Хэширование (англ hashing) — это метод разделения большого количества возможных входных значений на фиксированный набор выходных значений. В этом задании входным набором является набор всех дней рождения, а выходным набором — стулья с номерами от 1 до 31. Хеш-функция вычисляет выходное значение на основе каждого входа. Если входной набор больше выходного набора, то двум входным значениям может быть сопоставлено одно и то же выходное значение. Поэтому нам необходимо предложить механизм для разрешения таких столкновений (англ collision). Данное задание описывает решение, которое называется открытой адресацией, где в случае столкновений более позднее входное значение направляется на следующее значение выходного набора. Хеширование и его различные механизмы для разрешения столкновений используются при хранении данных в хеш-таблицах (англ hash table).

Аня, Боря, Вера и Гена решили приготовить большой завтрак. Они пошли в магазин, чтобы купить четыре продукта: яйца, сосиски, бобы и помидоры.
Всего они купили восемь товаров: две коробки яиц, две упаковки сосисок, две банки бобов и два помидора.
Каждый из них купил по два разных продукт питания, и при этом известно, что:
Если Аня и Гена купили один и тот же продукт питания, то что это за продукт?
[Raadionupud]
A. Коробка яиц
B. Упаковка сосисок
C. Банка бобов
D. Помидор
Правильный ответ: A (Коробка яиц).
Чтобы решить это задание, поэтапно составим таблицу истинности.
Первое утверждение гласит, что Аня купила коробку яйц, а Боря нет.
| Аня | Боря | Вера | Гена | |
|---|---|---|---|---|
| Яйца | 1 | 0 | ||
| Сосиски | ||||
| Бобы | ||||
| Помидор |
Второе утверждение гласит, что Вера и Боря купили по банке с бобами. Поскольку покупается только две банки бобов, то их, следовательно, не могут купить ни Аня, ни Гена.
| Аня | Боря | Вера | Гена | |
|---|---|---|---|---|
| Яйца | 1 | 0 | ||
| Сосиски | ||||
| Бобы | 0 | 1 | 1 | 0 |
| Помидор |
Перескочим к четвёртому утверждению, которое гласит, что Боря не покупал сосисок. Поскольку Боря должен был купить два продукта питания, и он не купил ни сосисок, ни яиц, то он должен был купить помидор.
| Аня | Боря | Вера | Гена | |
|---|---|---|---|---|
| Яйца | 1 | 0 | ||
| Сосиски | 0 | |||
| Бобы | 0 | 1 | 1 | 0 |
| Помидор | 1 |
Третье утверждение гласит, что Гена и Вера купили один и тот же продукт питания. Поскольку Аня уже купила одну коробку яиц, то Гена и Вера не могли их купить. Поскольку Боря купил одну банку бобов и один помидор, то, аналогично, Гена и Вера не могли купить ни бобов, ни помидор. Значит, продуктом питания, который купил и Гена, и Вера, была упаковка сосисок.
| Аня | Боря | Вера | Гена | |
|---|---|---|---|---|
| Яйца | 1 | 0 | ||
| Сосиски | 0 | 0 | 1 | 1 |
| Бобы | 0 | 1 | 1 | 0 |
| Помидор | 1 |
Теперь мы можем заполнить данными до конца столбец Ани. Вторым купленным Аней продуктом был помидор. Поскольку всего было куплено два помидора, то, следовательно, Вера и Гена не могли купить помидор.
| Аня | Боря | Вера | Гена | |
|---|---|---|---|---|
| Яйца | 1 | 0 | ||
| Сосиски | 0 | 0 | 1 | 1 |
| Бобы | 0 | 1 | 1 | 0 |
| Помидор | 1 | 1 | 0 | 0 |
Далее мы можем заполнить уже всю таблицу. Поскольку мы уже знаем, что именно купила Вера, то она уже не могла купить коробку яиц. Значит, коробку яиц купил Гена.
| Аня | Боря | Вера | Гена | |
|---|---|---|---|---|
| Яйца | 1 | 0 | 0 | 1 |
| Сосиски | 0 | 0 | 1 | 1 |
| Бобы | 0 | 1 | 1 | 0 |
| Помидор | 1 | 1 | 0 | 0 |
Следовательно, если спросить, что же это за продукт питания, который купила и Аня, и Гена, ответ мы получим, посмотрев на таблицу. Это коробка яиц.
Возможны и другие пути решения этого задания. Например, если мы изучим данные факты в другой последовательности и заполним ячейки таблицы в другом порядке. Логическое представление информации также имеет несколько вариантов. Например, вместо таблицы истинности можно было бы использовать граф, который визуализировал бы данные по-другому.
Это задание является примером логической задачи. Имея неполную информацию о том, что четверо друзей купили в магазине, мы можем использовать дедуктивное рассуждение для выяснения, какой же один и тот же продукт питания купили Аня и Гена. Логика — это также важная часть программирования. Наиболее часто мы используем логику в программах при создании условий (if-операторов), но логику можно использовать и, например, для уменьшения пространства поиска, чтобы программа могла решить задачу гораздо эффективнее.
При решении данного задания было полезно составить таблицу истинности. Преимущество табличного представления в том, что оно указывает нам, какой информации нам ещё не хватает. Часто выбор удачного способа представления данных помогает легче решить задачу и в программировании.

Четыре элемента должны быть размещены в квадрате 2x2 так, чтобы элементы касались друг друга только сторонами с одинаковыми символами. Один из возможных способов таков:
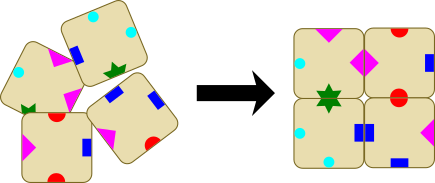
Теперь у нас имеется пять элементов.

Из этих пяти элементов нужно выбрать четыре и разместить их, следуя описанному выше правилу. В этом случае есть только один вариант для выбора подходящих четырёх элементов.
Какой элемент в данном случае не будет использован?
[Raadionupud]
A. Элемент A
B. Элемент B
C. Элемент C
D. Элемент D
E. Элемент E
Правильный ответ: C (элемент C).
Используя элементы A, B, D и E, и следуя описанному правилу, можно создать квадрат 2x2:
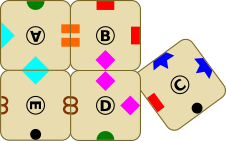
Один из подходов — это перепробовать разные варианты, пока один из них не сработает. Однако количество проверяемых комбинаций можно и уменьшить.
Сделаем это в два отдельных шага.
Сначала построим граф из пяти элементов и соединим линиями только те элементы, у которых есть хотя бы один одинаковый символ. Например, мы можем соединить линией элементы C и E, потому что у них обоих есть маленький чёрный кружок на одной стороне, а элементы A и C мы не можем соединить, потому что ни один из символов элемента A не присутствует на элементе C.
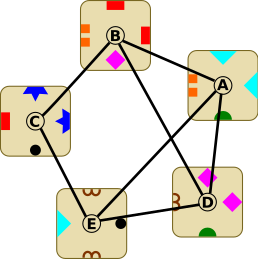
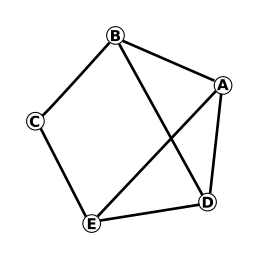
Если мы сможем найти путь от элемента к элементу, который вернётся обратно к первому элементу через четыре шага, то мы и найдём возможное решение.
Воспользуемся вспомогательной схемой и выясним все возможные циклы, имеющие длину в четыре шага. Таких циклов в нашем графе три:
Разумеется, равнозначны и все циклические пермутации пяти букв (т.е. начинающиеся с любой буквы, но сохраняющие порядок), и их варианты наоборот. Например, A-B-C-E-A, B-C-E-A-B и E-C-B-A-E будут равнозначными.
Возможно ли, что предложенный во вспомогательной схеме второй или третий вариант (A-B-C-E-A или B-C-E-D-B) мог привести нас к решению головоломки?
Оба цикла содержат тройник B-C-E, и существует только два способа соединить эти элементы в таком порядке:
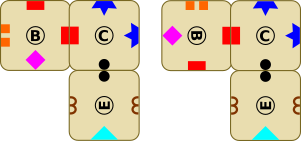
Однако в обоих случаях ни элемент A, ни элемент D не могут использоваться в качестве четвёртого элемента.
Эти посторонние решения возникли на предыдущем шаге, потому что при составлении графа мы учитывали только то, какие символы есть на каждом элементе, но не учитывали расположение этих символов на элементах.
Для решения проблемы часто полезно (временно) игнорировать некоторые её детали. Такой подход называется абстракцией. В данном задании на первом этапе мы игнорировали расположение символов на элементах; нас интересовало только то, есть ли у двух элементов общие символы. Получившаяся схема (граф) уже дала нам достаточно информации, чтобы сделать поиск решения немного короче, оставив только три возможных решения.
Графы часто используются в информатике как абстракция обрабатываемых данных. На протяжении всей истории многие люди использовали умные и быстрые методы для определения различных свойств таких графов, таких как простое нахождение всех циклов заданной длины.
Для дальнейшего решения задания нам понадобился второй шаг, в котором снова использовался граф как абстракция проблемы. Разбиение сложной задачи на отдельные этапы, которые легче решить, называется декомпозицией — опять-таки, это важный навык вычислительного мышления.

Бобр Марк ищет номер телефона своего друга на очень длинной интернет-странице. Марк не уверен, как точно пишется имя друга, поэтому использует для поиска специальные символы:
| Символ | Значение |
|---|---|
| ? | точно одна неизвестная буква |
| & | точно две неизвестные буквы подряд |
| % | любое количество неизвестных букв до конца имени |
Например, поисковый запрос «Ma%» может выдать имена Maрия, Maрк и т.д.
Какие из следующих имён выдаст поисковый запрос «S?rah B&cht%»?
(Отметьте все правильные ответы.)
[Märkeruudud]
A. Sarah Birchtree
B. Sara Benchton
C. Sarah Bilchman
D. Sirah Beachtram
Правильный ответ: A, D.
Вариант A правильный, потому что имя «Sarah Birchtree» соответствует поисковому запросу «S?rah B&cht%»:
Вариант B не может быть правильным, потому что в имени «Sara» отсутствует буква «h».
Вариант C не может быть правильным, потому что в фамилии «Bilchman» вместо «cht» имеется «chm».
Вариант D правильный, потому что буквы имени и фамилии соответствуют используемому запросу: «S» и «S», «i» и «?», «rah» и «rah», пробел и пробел, «B» и «B», «ea» и «&», «cht» и «cht», а также «ram» и «%».
Многие информационные системы позволяют использовать для поиска информации так называемые символы подстановки (англ wildcard) или символы-джокеры. Примером их использования были специальные символы, которые были описаны в этом задании. Также во многих командах Windows, MacOS и Linux для одновременного именования нескольких файлов можно использовать «?», что означает «только один неизвестный символ», и «*», что означает «любое количество неизвестных символов».
Другой пример: многие программы обработки текста позволяют использовать так называемые регулярные выражения (англ regular expression). Эти выражения позволяют описать шаблоны, которые используются для поиска или замены текста.
Такие инструменты позволяют сэкономить время, потому что команда может быть одновременно применена ко многим файлам или словам. Без них команду пришлось бы давать отдельно для каждого файла или каждого возможного слова.

У бобра Максима в электронной таблице есть данные и формулы.

Теперь на основании вычисленных по формулам значений (в строке 3) он строит диаграммы.
Какую из приведенных ниже диаграмм Максим никогда не получит на основании этих данных?
[Raadionupud]
A. 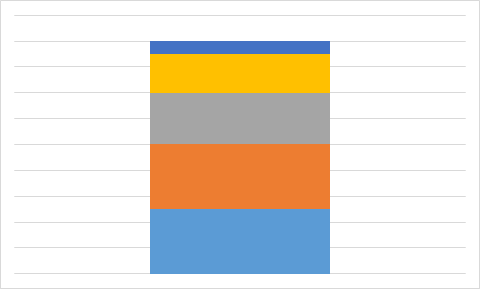
B. 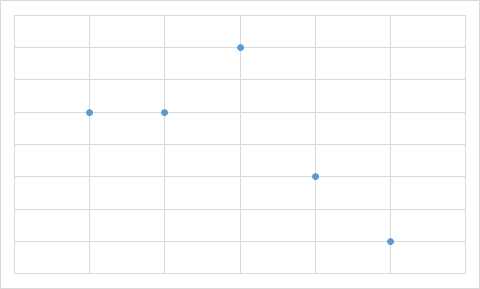
C. 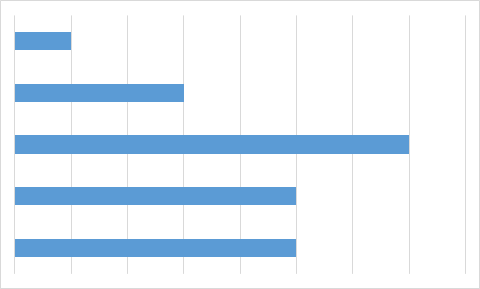
D. 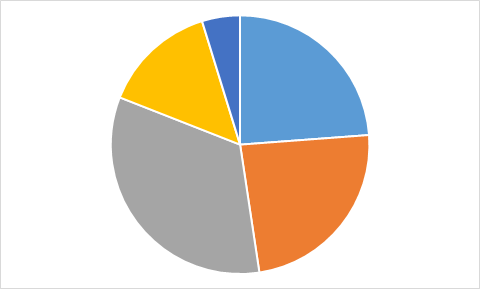
Правильный ответ: A.
Чтобы найти ответ, не нужно даже вычислять значения всех ячеек с формулами. Достаточно заметить, что на трёх диаграммах только одно значение является максимальным, а два следующих (по величине) значения — одинаковы. Однако на диаграмме А есть именно два равных максимальных значения. Поэтому диаграмма А определённо не составлена по тем же данным, что используются в остальных диаграммах.
При обработке данных может случиться так, что что-то случайно пойдёт не так. Именно поэтому всегда полезно посмотреть на результат своей работы и подумать, если там что-то такое, что явно не сходится или не подходит.

Интернет-магазин одежды использует систему рекомендаций, которая базируется на персональных данных покупателей. Например, если клиент хочет купить обувь, то программа следует приведённым ниже правилам и рекомендует купить сапоги:
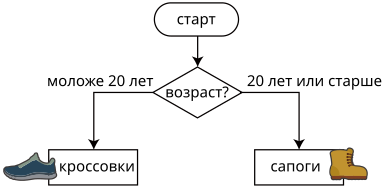
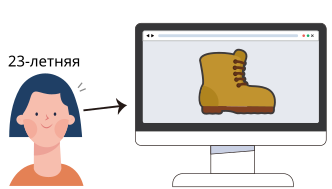
Однажды часть правил, на которых основывались рекомендации по одежде, были случайно удалены. На нижеприведённом рисунке показана оставшаяся часть правил.

К счастью, некоторые ранее данные рекомендации сохранились:
| Клиент | Рекомендация | |
|---|---|---|
| 18-летняя 140 см |
Однотонная юбка |  |
| 32-летняя 145 см |
Пёстрая юбка |  |
| 28-летний 155 см |
Пёстрые штаны |  |
| 15-летний 160 см |
Однотонные штаны |  |
| 10-летняя 152 см |
Однотонные штаны |  |
Основываясь на вышеприведённой информации, какой может быть недостающая часть рисунка?
[Raadionupud]
A. 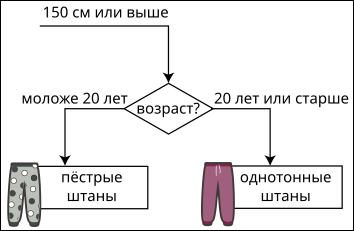
B. 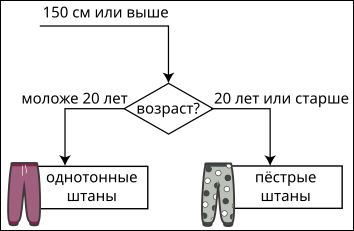
C. 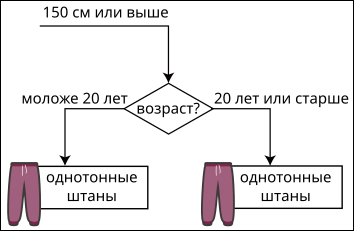
D. 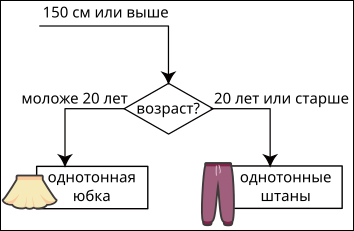
Правильный ответ: B.
Первое условие проверяет рост клиента, поэтому нам нужно учитывать только клиентов ростом не ниже 150 см:
| Клиент | Рекомендация | |
|---|---|---|
| 28-летний 155 см |
Пёстрые штаны |  |
| 15-летний 160 см |
Однотонные штаны |  |
| 10-летняя 152 см |
Однотонные штаны |  |
В таблице видно, что всем этим покупателям рекомендовали купить штаны, поэтому вариант D неверен.
Поскольку всем покупателям моложе 20 лет рекомендовали купить однотонные штаны, то вариант А неверен.
Поскольку всем клиентам в возрасте 20 лет и старше рекомендовали купить пёстрые штаны, то вариант C неверен.
Мы видим, что клиенты высокого роста получали разные рекомендации о покупке штанов в зависимости от их возраста, поэтому полная картина должна выглядеть так:

Используемая в этом задании схема называется деревом решений (англ decision tree). Это более простой частный случай блок-схемы (англ flowchart).
В информатике блок-схема может использоваться для представления алгоритма, рабочего потока или процесса. Блок-схема состоит из различных фигур, соединённых стрелками. Фигуры обозначают различные типы операций, а стрелки обозначают порядок, в котором эти операции выполняются.
Блок-схемы и деревья решений также часто используются для предоставления людям различных инструкций к действиям, например, как действовать в случае чрезвычайной ситуации, учитывая текущие обстоятельства, или для объяснения того, как следует претворить в жизнь определённые планы.

Коламы — это декоративные узоры, которые можно нарисовать на полу, например, с помощью мела. Чтобы нарисовать колам, сначала отмечают несколько точек, а затем рисуют вокруг них линии. Каждая линия начинается и заканчивается в одной и той же точке, мел во время рисовании не отрывается от пола.
Линия может пересекать другие линии или саму себя, но не может совпадать или даже касаться другой линии, не пересекая её. Каждая линия должна быть нарисована вокруг хотя бы одной точки. Каждая линия, нарисованная таким образом, называется петлей.
Колам, показанный ниже, имеет 6 петель. Обратите внимание, что петли пересекаются в разных местах, а петля чёрного цвета также пересекает саму себя.
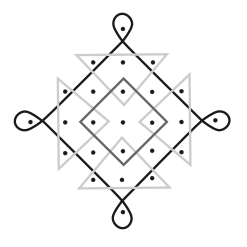
Какой из следующих коламов имеет наименьшее количество петель?
[Raadionupud]
A. 
B. 
C. 
D. 
Правильный ответ: D.
В варианте A имеется 4 петли:
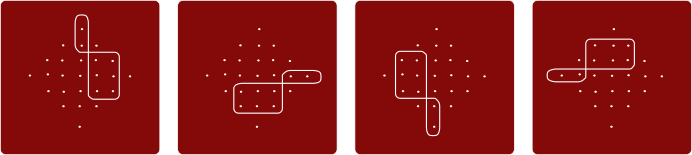
В варианте B имеется 5 петель:

В варианте C имеется 3 петли:
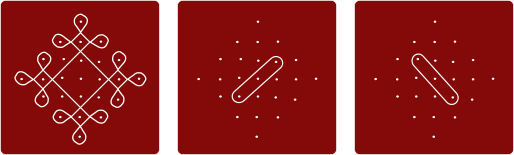
В варианте D только одна петля; для наглядности покажем, как нарисовать этот колам поэтапно:

Коламы — это замысловатые узоры, которые можно найти в индийских городах и деревнях. Как запоминаются и рисуются эти узоры? Одна из теорий гласит, что они создаются по простым правилам, которые передаются из поколения в поколение.
Генерация текстов, которые соответствуют наборам правил, изучается в информатике в рамках теории формальных языков. Хотя изначально генеративные грамматики были предназначены для описания текстов (представляющих из себя одномерные строки символов), позже эта идея была распространена на многомерные объекты, включая графические изображения. Такие методы также часто используются в процедуральном искусстве (англ generative art).

Рассмотрим изображение, состоящее из 6x5 квадратов, где некоторые квадраты чёрные, а некоторые — белые:
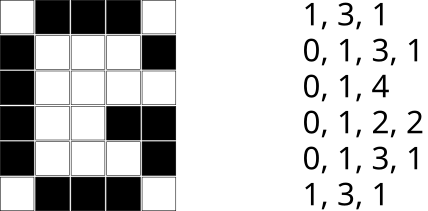
Это изображение можно преобразовать в последовательность чисел, подсчитав для каждой строки, сколько квадратов последовательно окрашено в белый цвет, а затем сколько квадратов последовательно окрашено в чёрный цвет, далее сколько квадратов последовательно окрашено в белый цвет и т.д., пока мы не достигнем конца строки. Обратите внимание, что если строка начинается с чёрного квадрата, то количество белых квадратов в начале этой строки равно 0.
В самом конце мы должны объединить все числа, которые получились для каждой строчки, в одну последовательность чисел. В случае вышеприведённого изображения получится следующая последовательность: 1, 3, 1, 0, 1, 3, 1, 0, 1, 4, 0, 1, 2, 2, 0, 1, 3, 1, 1, 3, 1.
Kакое изображение, состоящее из 6x5 квадратов, будет представлено последовательностью 1, 4, 0, 1, 4, 1, 3, 1, 4, 1, 0, 1, 3, 1, 1, 3, 1?
[Raadionupud]
A. 
B. 
C. 
D. 
Правильный ответ: D.
При решении мы можем следовать заданной последовательности, рисуя соответствующую матрицу 6x5. Когда строка заполнена, нам нужно перейти к следующей строке, начиная снова с белого цвета.
На нижеприведённом изображении показан правильный ответ. Также показано деление последовательности на фрагменты каждой строки.
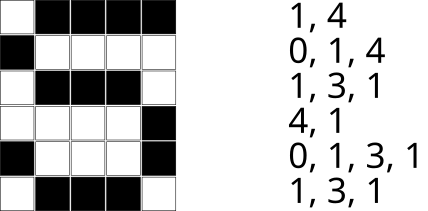
Вариант A неправильный, потому что его последовательность была бы 0, 4, 1, 1, 1, 3, 1, 1, 3, 1, 1, 1, 2, 1, 1, 2, 1, 2, 2, 1.
Вариант B неправильный, потому что его последовательность была бы 1, 4, 4, 1, 1, 3, 1, 0, 1, 4, 0, 1, 3, 1, 1, 3, 1.
Вариант C неправильный, потому что его последовательность была бы 4, 1, 1, 2, 2, 0, 1, 2, 1, 1, 0, 1, 2, 1, 1, 0, 1, 2, 1, 1, 1, 2, 2.
Для хранения или передачи изображений между электронными устройствами необходимо преобразовать их в числа. Есть много способов сделать это, и в этом задании показан один из них. Используя одно число для представления последовательности квадратов одного и того же цвета, этот метод сжимает данные, т.е. уменьшает объём данных, а это имеет важное значение в информатике. Этот метод можно улучшить несколькими способами, например, позволив числу ссылаться на последовательность, которая охватывает квадраты более чем одной строки.
Поиск способов представления данных был сложной задачей с момента появления первых электронных устройств. Выбор способа может повлиять на время, необходимое для обработки или отправки и получения информации. Сегодня эта проблема по-прежнему актуальна, особенно в Интернете: создание новых способов кодирования изображений, видео и других медиафайлов может ускорить нашу работу в Интернете.
Описанный в этом задании метод использовался старыми факсами для передачи содержания документов.
Copyright © 2022 Bebras – International Challenge on Informatics and Computational Thinking.
Licensed under Creative Commons Attribution-ShareAlike 4.0 International License.
Flag icons by GoSquared.