

Veroonika armastab hüpata. Ta leidis 17 ruutu, mis asetsevad ühel joonel, ja koostas nendest mänguplaani.
Veroonika pani mündi ruudustiku ühte otsa ja seisis ise teise otsa, näoga mündi poole.
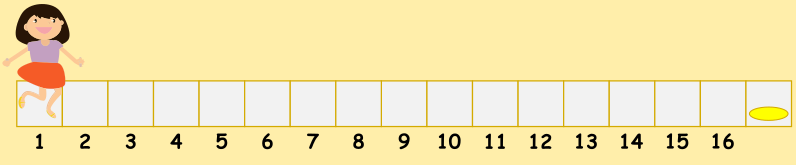
Ta soovib hüpata rea igale ruudule, järgides järgmisi reegleid:
Eesmärk on neid reegleid arvestades kõigi teiste ruutude külastamise järel mündi juurde jõuda.
Millistesse ruutudesse peaks selleks olema märgitud "O"?
(Sisesta tühikutega eraldatud arvud kasvavas järjekorras, näiteks 2 6 12 15.)
[Tekstikast]
Õige vastus on: 3 4 7 8 11 12 15 16.
Hüppamise järjekord on tähistatud nooltega.
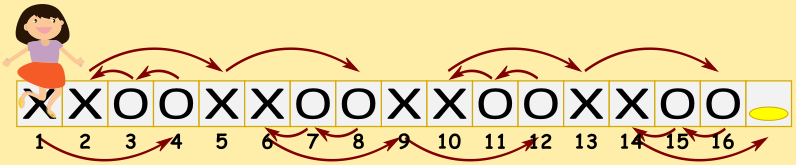
Kuna tagasi saab liikuda ainult ühe ruudu kaupa, on ülesandel ainult üks lahendus. Kui Veroonika hüppaks edasi rohkem kui kaks korda järjest, jääks tal mõned vasakpoolsed ruudud külastamata ja ta ei saaks enam nende juurde tagasi pöörduda.
Toimingute järjekorra leidmist eesmärgi saavutamiseks vastavalt etteantud reeglitele nimetatakse algoritmiseerimiseks. Roboti või arvutirakenduse saab programmeerida nii, et see töötaks etteantud reeglite järgi. Kui vajame tulemuseks konkreetset väljundit, peame määrama ka sobiva sisendi. Oletame, et meil on pikk kitsas L-kujuline koridor ning meie puhastusrobot suudab minna ainult otse ja keerata 90° paremale, peame selle panema L-tähe lühema osa otsa, muidu ei saa tervet koridori puhtaks.

Vaja on moodustada kümnekohaline arv, kasutades iga numbrit (0–9) täpselt üks kord. Saadud arv peab olema vähim, mis vastab kõigile järgmistele tingimustele:
0→9, 1→0, 1→2, 1→6, 2→3, 3→5, 3→4, 6→5, 5→7, 7→8, 9→7.
Tingimus a→b tähendab, et number a peab moodustatavas 10-kohalises arvus asuma numbrist b vasakul.
Milline on vähim kümnekohaline arv, kus on kasutatud iga numbrit täpselt üks kord ning mis vastab antud tingimustele?
[Täisarv]
Õige vastus on: 1023465978.
Kuidas me saame selle arvu usaldusväärselt kindlaks teha? Esitame tingimused graafina, kus graafi tippudeks on numbrid, nende vahel aga suunatud servad (kaared) vastavalt antud tingimustele.
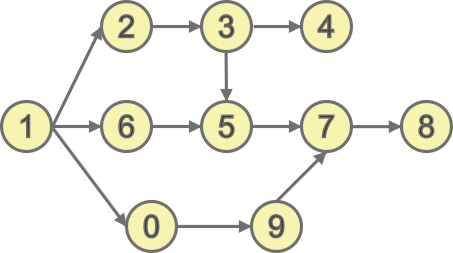
Otsitav arv peab algama numbriga, millel puudub sissetulev nool: siis pole tingimust, mis nõuaks, et mõni teine number peaks olema sellest vasakul. Nii moodustame kogu arvu järgmise algoritmi abil.
Kuni on veel kasutamata numbreid, kordame järgmisi samme:
Selle algoritmi täitmisel läbitakse graafi tippe punaste numbritega tähistatud järjekorras. Seega annab algoritm tulemuseks arvu 1023465978.
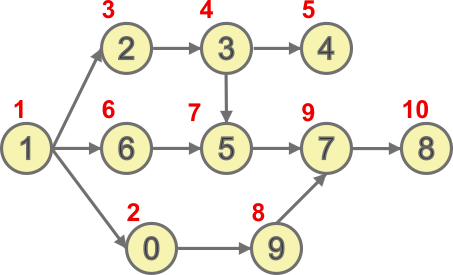
Selles ülesandes anti meile ainult osaline teave selle kohta, kuidas numbreid tuleks soovitud arvu moodustamiseks kokku panna, kuid siiski paluti meil moodustada arv täielikult järjestatud numbrijadana. Matemaatikas nimetatakse objektide (numbrite või muude) täielikult järjestatud jada, mis rahuldab mingit osalist järjestamistingimust, nende objektide topoloogiliseks järjestuseks (ingl topological sorting). Vastuse selgituses kasutatud algoritm on standardmeetod, millega topoloogiline järjestus leida või tuvastada, et see on võimatu. Kas taipate, miks ei ole võimalik koostada arvu, mis vastaks tingimustele 2→4, 4→3, 3→2?

Väike kobras on labürindis, mis koosneb kahest korrusest. Korruste plaanid on erinevad.
Kobras saab liikuda oma asukohast samal korrusel olevasse naaberruutu, kui ruutude vahel pole seina. Iga selline samm võtab ühe sekundi. Kobras saab võlukepi abil liikuda ka teise korruse samas kohas olevasse ruutu, kuid selleks kulub viis sekundit.
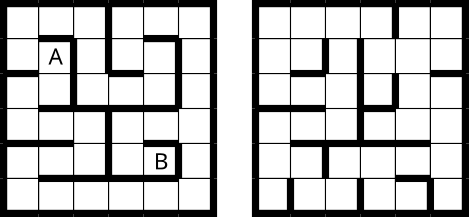
Näiteks kui kobras on ruudus A, on tal kolm võimalikku käiku:
Kobras alustab ruudust A ja soovib jõuda ruutu B nii kiiresti kui võimalik.
Milline on vähim aeg, millega kobras võib jõuda ruudust A ruutu B?
[Raadionupud]
A. 16 sekundit
B. 17 sekundit
C. 18 sekundit
D. 20 sekundit
Õige vastus on: C (18 sekundit).
See on lühima tee leidmise ülesanne. Lahenduse leidmiseks on erinevaid lähenemisviise, millest üks on nn Dijkstra algoritm (ingl Dijkstra's algorithm), mis leiab lühimad teed antud algusruudust kõigisse teistesse ruutudesse.
Alloleval pildil on näidatud kõigi ruutude kaugused (lühimate teede pikkused) ruudust A.
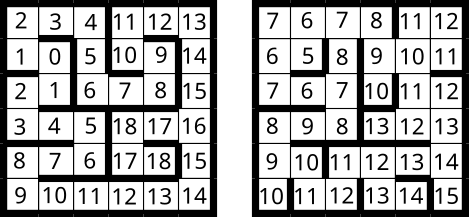
Näha on, et ruudu B kaugus on 18. Üks võimalikest optimaalsetest teedest on järgmine:
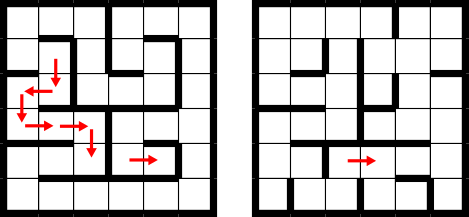
Vastus D (20 sekundit) vastab optimaalsele teele, kui kobras liiguks ainult ühe korruse piires.
Lühima tee leidmine on graafiteooria standardülesanne. Selle rakendusvõimaluste hulka kuuluvad optimaalse tee leidmine linnakaardil või arvutivõrgus, aga ka ühenduste loomine mikrokiipides. Meie ülesandes võtab korruste vahel liikumine rohkem aega kui ühe korruse sees liikumine (vastavalt 5 ja 1 sekundit). Ka mitmekihilistes mikrokiipides on tasandite vahelised ühendused kallimad kui ühe tasandi sisesed. Tänapäevased VLSI-kiibid kasutavad 10-kihilisele ränikristalle, samas kui meie ülesandes oli ainult kaks korrust. Samuti nõuab mikrokiipide ehitamine miljonite ja miljardite ühenduste tegemist.

Kuus kobrast elavad Kopralinna eri osades. Nad kasutavad metrood, et kohtuda ühes peamistest jaamadest A, B, C või D. Koprad alustavad sõitu erinevatest jaamadest korraga ja tahavad jõuda kohtumispaika võimalikult lühikese aja jooksul.
Metrooplaanil on näidatud igal liinil olevad jaamad (punased ringid) ja nende vahel liikumiseks kuluv aeg minutites. Lisaks võtab igas jaamas peatumine veel ühe minuti.
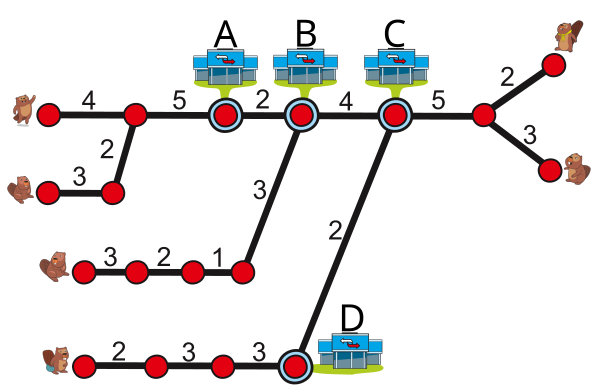
Millises jaamas peaksid sõbrad kokku saama, et üksteist võimalikult kiiresti näha?
[Raadionupud]
A. Jaamas A
B. Jaamas B
C. Jaamas C
D. Jaamas D
Õige vastus on: B (jaamas B).
Selle ülesande lahendamiseks peame välja arvutama iga kopra reisiminutid, alustades tema algusjaamast ja lõpetades iga jaamaga A, B, C, D. Seda saaks muidugi teha, arvutades iga sõbra jaoks välja kõikvõimalikud reisiajad ja vaadata, kui palju aega kulub viimase sõbra igasse jaama jõudmiseks, aga see oleks väga tüütu ja pikk töö.
Selle ülesande lahendamiseks saame kasutada dekompositsiooni (probleem jagamist väiksemateks osadeks) ja abstraktsiooni (otsustamist, millised marsruudid on arvutamiseks olulised, ignoreerides teisi marsruute). Peame arvestama iga marsruudi pikimate reisiaegadega, sest peame teadma, kui kaua kulub viimase sõbra saabumiseks.
Allpool näitame ühte võimalikku sammude jada selle ülesande lahendamiseks.
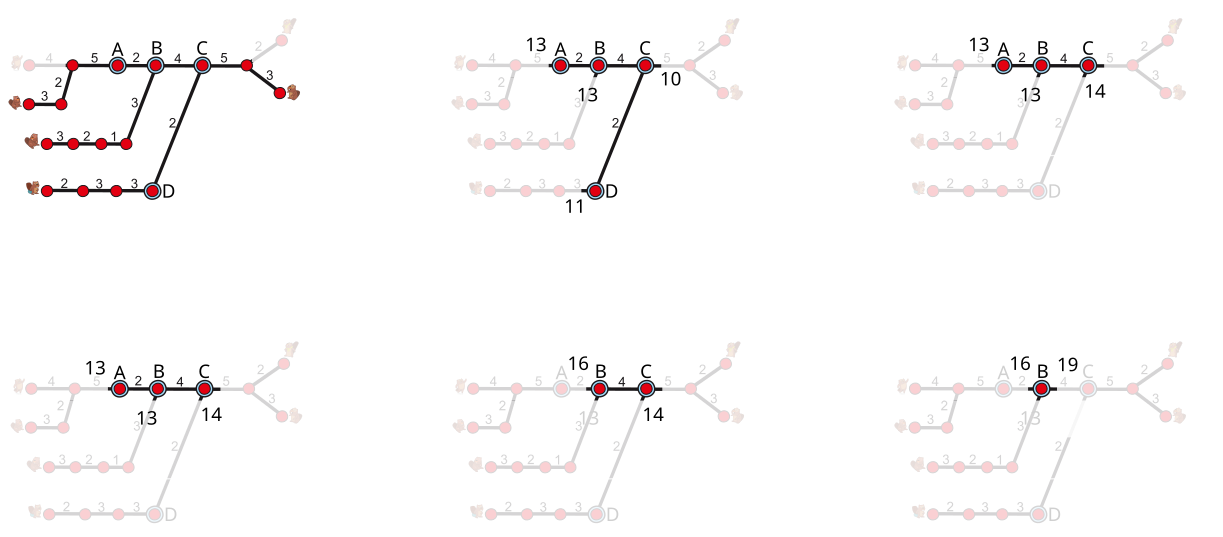
Vaadates plaanil kahe vasakpoolse sõbra võimalusi jaama A jõudmiseks, leiame, et esimesel sõbral kulub selleks 11 minutit (1+4+1+5) ja teisel sõbral 13 minutit (1+3+1+2+1+5). Nende sõprade sealt edasi jaamadesse B, C ja D sõitmise osas peame arvestama ainult aeglasema kohalejõudmise ehk 13 minutiga. Samamoodi kohtuvad kaks sõpra parempoolsetest jaamadest jaamas C 10 minuti pärast (1+3+1+5), kuid kuna kolmanda (plaanil all oleva) sõbra jaama C jõudmiseks kulub 14 (1+2+1+3+1+3+1+2) minutit, siis on meil sealt edasi vaja arvestada ainult 14 minutiga.
Jätkame samamoodi teiste jaamadega (vt. ülaltoodud joonist), võttes alati arvesse ainult pikimat saabumisaega, kuni jõuame lõppjaama B. See on parim jaam, kuhu kõik sõbrad saavad võimalikult lühikese ajaga ehk 19 minutiga kohale jõuda.
Meie tulemuse kinnitamiseks on allolevas tabelis toodud minutite arv, mis kulub sõpradel igast suunast igasse jaama jõudmiseks. Võrreldes jaamu, leiame, et viimase sõbra saabumine jaama A võtab aega 22 minutit, jaama B jaoks 19 minutit, jaama C jaoks 21 minutit ja jaama D jaoks 24 minutit. See kinnitab, et jaam B ongi parim kohtumispaik.
| Reisiaeg jaama A | Reisiaeg jaama B | Reisiaeg jaama C | Reisiaeg jaama D |
|---|---|---|---|
| Vasakult: 13 | Vasakult: 16 | Vasakult: 21 | Vasakult: 24 |
| Paremalt: 22 | Paremalt: 19 | Paremalt: 10 | Paremalt: 11 |
Informaatikas tähendab dünaamiline plaanimine (ingl dynamic programming) keeruka probleemi lihtsustamist, jagades selle lihtsamateks alamprobleemideks. Seda kasutatakse tihti optimeerimisülesannetes, kus on vaja leida kõigist võimalikest variantidest mingis mõttes parim (tavaliselt suurim või vähim).
Selles ülesandes kasutatud joonist nimetatakse graafiks (ingl graph), selle tippudeks (ingl vertex) on jaamad ja servadeks (ingl edge) neid ühendavad teed. Käesolev näide on kaalutud graafist (ingl weighted graph), kuna servadele on määratud väärtused (reisi kestus). Ülesande modelleerimisel graafina võivad kaalud tähistada selliseid parameetreid nagu kulu, pikkus, raskus või mahutavus.


Kobras käis õunu korjamas ja sai kokku 31 õuna. Ta tahab need viide kasti hoiule panna.

Ta tahab, et tulevikus oleks tal võimalik võtta mistahes arv õunu nii, et ta valib selleks ühe või mitu olemasolevast viiest õunakastist ja võtab valitud kastidest välja kõik õunad.
Kui palju õunu peaks kobras igasse kasti panema?
[Raadionupud]
A. 1, 3, 6, 9, 12
B. 1, 2, 4, 8, 16
C. 6, 6, 6, 6, 7
D. 1, 2, 3, 4, 5
Õige vastus on: B (1, 2, 4, 8, 16).
Vastuse leidmiseks peame jälgima, et kastides olevate õunte arvude liitmisel võiksime saada mistahes arvu 1 kuni 31.
Kuna vajame võimalust võtta üks õun, võime alustuseks panna esimesse kasti ühe õuna. Meil on vaja ka võimalust saada kaks õuna; selleks võime panna teise kasti kaks õuna. Praeguseks momendiks saame võtta kas ühe (valime esimese kasti), kaks (valime teise kasti) või kolm õuna (valime nii esimese kui ka teise kasti).
Järgmine arv, mille peame saama, on neli; selleks võimegi kolmandasse kasti panna neli õuna. Nüüd saame võtta nii ühe, kaks, kolm (nagu enne), neli (valime kolmanda kasti), viis (valime esimese ja kolmanda kasti), kuus (valime teise ja kolmanda kasti) kui ka seitse õuna (valime esimese, teise ja kolmanda kasti). Samal viisil jätkates jõuamegi lahenduseni, kus esimeses kastis on üks, teises kastis kaks, kolmandas kastis neli, neljandas kastis kaheksa ja viimases kastis kuusteist õuna. Sel viisil saame võtta mistahes arvu õunu (lõigus 1 kuni 31), valides mingi hulga oma viiest kastist.
Variant A ei ole õige, kuna pole kastide komplekti, milles oleks kokku näiteks kaks või viis õuna.
Samuti ei ole õige variant C, kuna me ei saa võtta ühtki kuuest õunast väiksemat hulka.
Õige pole ka variant D, kuna me ei saa võtta rohkem kui 15 õuna. Sel juhul ei pannud kobras kõiki oma õunu üldse kastidessegi!
See ülesanne on seotud kahendsüsteemiga (ingl binary numeral system), mis on kõige levinum arvutites kasutatav arvusüsteem. Nagu lahendusest näha, kasutasime arvu 2 astmeid (1, 2, 4, 8, 16), et saaksime esitada mistahes arvu lõigust 1 kuni 31 (tegelikult isegi 0 kuni 31, sest on ka võimalus mitte võtta ühtegi kasti ja saada null õuna). See on sarnane arvutiga, mis töötaks ainult arvudega, mida saab esitada 5 kahendnumbriga (5 bitiga):
| Bitt | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Astendaja (p) | 0 | 1 | 2 | 3 | 4 |
| 2p | 1 | 2 | 4 | 8 | 16 |
Viimane rida (2p) annab just õunte arvu meie lahenduse igas kastis.

Kopramängud on iga-aastane võistlus, mis koosneb kolmest voorust. Võistluse alguses on kõik 8 osalejat ühes grupis. Igas voorus jagatakse iga grupp loosiga pooleks ja pooled võistlevad üksteise vastu. Kaks esimest vooru on seega võistkondlikud, kolmas aga individuaalne. Iga võistluse võidab see võistkond, kelle liikmete punktide summa on suurem. Mängude üldvõitja on see, kes võidab kolm vooru järjest. Tänavuste Kopramängude õnnelik üldvõitja oli Anna.
Tabelis on toodud kõigi osalejate igas voorus teenitud punktid.
| Voor | Anna  |
Bruno  |
Carolin  |
Daisi  |
Eero  |
Feliks  |
Georg  |
Helen  |
|---|---|---|---|---|---|---|---|---|
| 1. voor | 15 | 16 | 19 | 18 | 17 | 20 | 19 | 19 |
| 2. voor | 20 | 27 | 30 | 24 | 28 | 24 | 30 | 30 |
| 3. voor | 10 | 14 | 11 | 15 | 16 | 13 | 9 | 12 |
Millised kolm kobrast kuulusid Anna esimesse võistkonda?
[Märkeruudud]
B. Bruno
C. Carolin
D. Daisi
E. Eero
F. Feliks
G. Georg
H. Helen
Õige vastus on: D, F, G (Daisi, Feliks ja Georg).
Kolmas voor on individuaalne. Kuna Georg on ainus mängija, kellel on Annast vähem punkte, pidid nad kolmandas voorus kohtuma ja teises voorus olema samas võistkonnas.
Anna ja Georgi punktide summa teises voorus on 50. See peab olema suurem kui teise kaheliikmelise võistkonna punktide summa. Daisi ja Feliks on ainsad, kelle punktide summa jääb alla 50. Seetõttu peavad nad olema esimeses voorus Anna ja Georgiga samas võistkonnas. Kuna me teame nüüd neid liikmeid, on meil vastus käes.
Aga kontrolliks võime siiski läbi arvutada:
Seega ongi Anna üldvõitja.
Kui püüda seda ülesannet algusest lõpu suunas lahendada, peaks läbi proovima palju võimalikke kombinatsioone ja iga kombinatsiooni puhul hindama mitme vooru tulemusi. See võtaks päris palju aega.
Sellistel juhtudel otsivad informaatikud ülesande lahendamiseks tõhusamaid meetodeid. Praegusel juhul annab tagantpoolt ettepoole lähenemine väga kiiresti õige lahenduse, nagu on eespool selgitatud.
Seda meetodit kasutatakse olukordades, kus otsitakse lahendust, mis peab vastama teatud piirangutele. Mõnel juhul kombineeritakse lahenduse leidmiseks edasi- ja tagasiotsing.

Kaheksanurga igasse tippu on kirjutatud kolm või neli tähte. Must nool osutab kaheksanurga keskpunktist mingile täherühmale. Noolt saab pöörata ainult päripäeva.
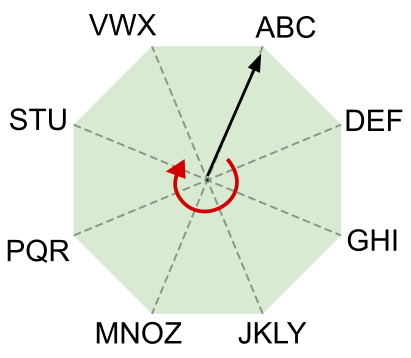
Kasutame seda kaheksanurka ja noolt sõnumite kodeerimiseks. Uue sõnumi kodeerimise alguses osutab nool täherühmale ABC. Edasi kodeerime sõnumi iga tähe nii, et:
Näiteks sõnumi "TREE" kodeerime jadaga 62-73-42-02.
Kuidas me kodeerime sõnumi "WATER"?
(Sisesta sidekriipsudega eraldatud numbripaarid, näiteks 12-23-34-45-56.)
[Tekstikast]
Õige vastus on: 72-11-62-32-43.
Õige vastuse saame, kodeerides sõnumi "WATER" tähthaaval. Sõnumi kood sisaldab 5 numbripaari:
Sõnumi kood on seega 72-11-62-32-43.
Üks meetod andmete kaitsmiseks volitamata isikute eest on šifreerimine. Salakirjateadus e krüptograafia (ingl cryptography) sai alguse juba 3500 aastat tagasi. Üks lihtsamaid šifreid on iga tähe asendamine mingi teise tähega. Selline nn asendusšiffer (ingl substitution cipher) on kergesti lahti murtav, kuna igas keeles on erinevate tähtede esinemissagedused erinevad ja selle põhjal on üsna lihtne tuvastada enamkasutatavate tähtede koodid.
Meie ülesandes on kasutusel meetod, mis noole pöörlemise tõttu annab ühe tähe jaoks erinevad koodid vastavalt sellele, milline täht on sõnumis eelmine. Sellega tekib šifris mõningane varieeruvus ja seda on raskem lahti murda. Samas on šiffer aga piisavalt lihtne, et seda kergesti meelde jätta.
Kui me jagaks tähed gruppidesse teistmoodi või paigutaks gruppe kaheksanurga tippudesse teises järjekorras, saaksime samale sõnumile erinevaid koode. Šifreerimisskeemi sellist seadistust nimetatakse šifreerimisvõtmeks (ingl encryption key) ja selle äraarvamist krüptoanalüüsiks (ingl cryptoanalysis).

Klassis on 31 tooli. Need asuvad ringikujuliselt ja on nummerdatud arvudega 1 kuni 31, nagu on näha joonisel.
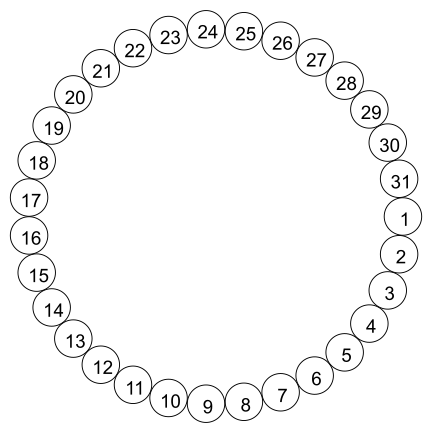
Lapsed mängivad järgmiste reeglitega mängu:
Oletame näiteks, et Teele ja Tuuli on kaksikud, kes on sündinud 20. aprillil, Tõnu on sündinud 21. jaanuaril ja Toomas 22. septembril.
Kui nad saabuvad järjekorras Teele, Tuuli, Toomas, Tõnu, siis istub Teele toolile 20, Tuuli toolile 21, Toomas toolile 22 ja Tõnu toolile 23.
Kui nad saabuvad aga järjekorras Tuuli, Tõnu, Toomas, Teele, siis istub Tuuli toolile 20, Tõnu toolile 21, Toomas toolile 22 ja Teele toolile 23.
Nüüd on klassi sisenenud kuus last ja nad istuvad tabelis näidatud viisil:
| Nimi | Sünnipäev | Tooli number |
|---|---|---|
| Anna | 11. mai | 13 |
| Berta | 12. veebruar | 12 |
| Cathy | 14. september | 14 |
| David | 11. august | 11 |
| Eero | 13. aprill | 15 |
| Feliks | 12. juuli | 16 |
Milline järgmistest väidetest ei saa olla tõene?
[Raadionupud]
A. Cathy istus esimesena
B. Feliks istus viimasena
C. Eero istus enne Annat
D. Berta istus enne Davidit
Õige vastus on: C (Eero istus enne Annat).
Cathy istub oma sünnipäevale vastaval toolil, nii et ta võis olla esimesena siseneja. Seega variant A võib olla tõene väide.
Selleks, et maanduda toolil 16, pidi Feliks saabuma pärast neid, kes istuvad toolidel 12–15. David istub toolil 11, seega pidi ta saabuma enne Annat, kellel on temaga sama sünnikuupäev. Seega on variant B kindlasti tõene väide.
Kui Eero oleks tulnud enne Annat, oleks tool 13 olnud vaba ja Eerol poleks olnud vaja istuda toolile 15. Seega ei saa variant C olla õige.
Berta ja David istuvad mõlemad oma sünnikuupäevale vastavatel toolidel ja võisid saabuda ükskõik kummas järjekorras. Seega variant D võib olla õige väide.
Räsimine (ingl hashing) on meetod suure hulga võimalike sisendväärtuste jagamiseks fikseeritud väljundväärtuste hulgale. Selles ülesandes on sisendhulk kõigi sünnipäevade kogum ja väljundhulk toolid numbritega 1 kuni 31. Räsifunktsioon arvutab iga sisendi põhjal väljundi. Kui sisendhulk on suurem kui väljundhulk, võidakse kahe sisendiga vastavusse panna sama väljund, seega peame pakkuma mehhanismi selliste kokkupõrgete (ingl collision) lahendamiseks. Ülesanne kirjeldab lahendust nimega avatud adresseerimine, mille puhul suunatakse kokkupõrke korral hilisem saabuja väljundhulgas järgmistele väärtustele. Räsimist ja selle erinevaid kokkupõrgete lahendamise viise kasutatakse andmete salvestamisel paisktabelites (ingl hash table).

Toomasel on kalliskivide kollektsioon. Tal on nende hulgas ka kindel eelistuste järjekord.
Saara teab, millised kalliskivid on Toomase kollektsioonis, kuid ta ei tea, kuidas need on järjestatud. Tal on plaan välja selgitada, milline kalliskivi on Toomase lemmik.
Saara valib välja neli Toomase kalliskivi ja küsib Toomaselt: "Milline neist neljast on sinu lemmik?". Siis valib Saara uue neljast kalliskivist koosneva komplekti ja esitab oma küsimuse uuesti. Seejärel valib ta kolmanda neljast kalliskivist koosneva komplekti ja esitab oma küsimuse viimast korda. (Mõni kalliskivi võib olla ka rohkem kui ühes Saara komplektis.)
Milline on suurim võimalik kalliskivide arv Toomase kollektsioonis, et Saara saaks tema lemmiku sel viisil kindlaks teha?
[Raadionupud]
A. 8 kalliskivi
B. 10 kalliskivi
C. 11 kalliskivi
D. 12 kalliskivi
Õige vastus on: B (10 kalliskivi).
Kümne kalliskivi puhul saab Saara Toomaselt kahe esimese päringuga küsida kaheksa erineva kalliskivi kohta. Toomase lemmik kummaski komplektis võib olla ka tema lemmik kogu kollektsioonis, kuid ülejäänud kolm kalliskivi kummastki komplektist ei saa seda olla. Seetõttu saab Saara kolmanda ja viimase küsimuse esitada komplekti kohta, milles on nii need kaks eelmistest küsimustest alles jäänud kandidaati kui ka need kaks kalliskivi, mille kohta ta pole veel küsinud. Toomase vastus kolmandale küsimusele ongi tema lemmikkalliskivi.
Sellega oleme näidanud, et Saaral on olemas strateegia, mis töötab, kui kollektsioonis on 10 kalliskivi. (Selliseid strateegiaid on ka teisi.) Näitame nüüd, et suurema kalliskivide arvu korral sobivat strateegiat ei ole. Selleks oletame, et Toomasel on vähemalt 11 kalliskivi ja keskendume Saara kahele esimesele küsimusele.
Kui neis komplektides on vähemalt üks ühine kalliskivi, on pärast kaht esimest küsimust analüüsimata veel vähemalt neli kalliskivi. Sel juhul peab Saara küsima nende nelja analüüsimata kalliskivi kohta, sest kui ta seda ei tee, võib just üks neist olla Toomase lemmik. Saara saab nüüd küll teada, milline on Toomase lemmik nende hulgas, kuid tal pole selle võrdlust ülejäänud seitsme juba analüüsitud kalliskiviga. Seega ei suuda tema strateegia kindlaks teha, milline kalliskivi on Toomase lemmik.
Kui Saara kahel esimesel komplektil ühiseid kalliskive pole, siis jäävad kandidaatide hulka kahe esimese küsimuse vastustena saadud kalliskivid ja kolm ülejäänud analüüsimata kalliskivi. Saara ei saa allesjäänud ühe küsimusega nende viie kandidaadi hulgast lemmikut välja selgitada.
Sellega oleme näidanud, et Saaral ei saa olla kolme küsimusega strateegiat, mis töötab, kui kalliskive on üle 10.
See ülesanne puudutab algoritme, millele kehtivad piirangud. Saara võib esitada ainult kolm küsimust ja iga küsimusega uurida ainult nelja kalliskivi. Nende piirangute tõttu leidub algoritm, mis töötab kuni 10 kalliskivi korral, aga pole olemas algoritmi, mis töötaks õigesti suurema hulgaga.
Praktikas võivad algoritmidel olla mitmesugused piirangud erinevatel põhjustel. Näiteks mingi masina või seadme hädapidurit juhtiv algoritm peab kindlasti reageerima enne, kui masin kellelegi viga teeb. Sellistes seadmete juhtarvutites kasutatakse sageli spetsiaalseid nn reaalaja operatsioonisüsteeme (ingl real-time operating system, RTOS). Teine võimalik piirangute allikas on see, et mõned operatsioonid võivad olla väga kallid, näiteks vajada kalleid abimaterjale või kulutada hinnalisi seadmeid.
See, kui mõni algoritm töötab õigesti ainult piiratud tingimustes (näiteks meie ülesandes sai Saara kolme küsimusega leida lemmiku maksmaalselt 10 kalliskivi hulgast), pole alati suur puudus. Küll aga peavad algoritme rakendavad insenerid olema neist piiridest teadlikud ja hoolitsema selle eest, et algoritmide rakendamisel neid piire ei ületata.

Meil on kuus pusletükki, kõik täpselt sama kujuga:

Kõigi nende tükkide väljaulatuvad osad sobivad ideaalselt teiste tükkide sisselõigetega.
Järgime algoritmi:
Milline järgmistest kujunditest ei saa olla loodud seda algoritmi järgides?
[Raadionupud]
A. 
B. 
C. 
D. 
Õige vastus on: D.
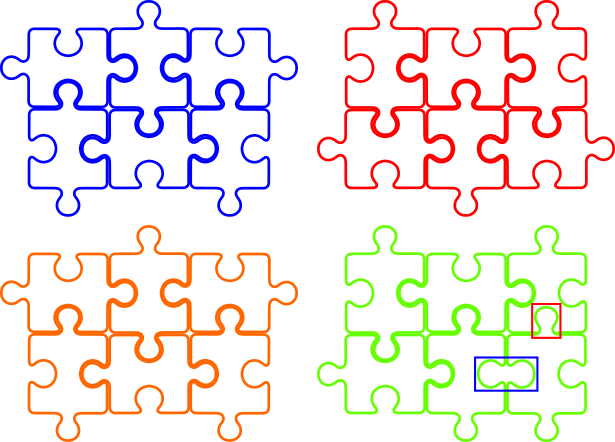
Algoritmi loomisel peaksime alati huvi tundma, millises olekus see lõpeb. Kui me algoritmist tõesti aru saame, suudame sageli ennustada lõppseisundit ilma kõiki samme läbimata. Kui leiame mõne märgi või atribuudi, mis muutub algoritmi täitmisel erinevates lahendustes erinevalt, saame seda kasutada õige lahenduse leidmiseks.

Madis otsib väga pikalt veebilehelt oma sõbra telefoninumbrit. Ta pole kindel, kuidas sõbra nime täpselt kirjutatakse, seepärast kasutab ta otsimisel erimärke:
| Märk | Tähendus |
|---|---|
| ? | täpselt üks tundmatu täht |
| & | täpselt kaks järjestikust tundmatut tähte |
| % | mistahes arv tundmatuid tähti kuni nime lõpuni |
Näiteks otsing "Ma%" leiaks nimed Madis, Marta jne.
Millised järgnevatest nimedest leiab otsing "S?rah B&cht%"?
(Märgi kõik õiged vastused.)
[Märkeruudud]
A. Sarah Birchtree
B. Sara Benchton
C. Sarah Bilchman
D. Sirah Beachtram
Õige vastus on: A, D.
Variant A on õige, sest nimi "Sarah Birchtree" vastab otsingule "S?rah B&cht%":
Variant B ei ole õige, sest eesnimes "Sara" ei ole "h"-tähte.
Variant C ei ole õige, sest perenimes "Bilchman" on "cht" asemel "chm".
Variant D on õige, sest "S" ja "S", "i" ja "?", "rah" ja "rah", tühik ja tühik, "B" ja "B", "ea" ja "&", "cht" ja "cht" ning "ram" ja "%" kõik vastavad.
Paljud infosüsteemid võimaldavad info otsimiseks kasutada selles ülesandes kirjeldatud erimärkidele sarnaseid nn metamärke (ingl wildcard) ehk jokkereid. Näiteks nii Windowsi, MacOSi kui Linuxi paljudes käskudes on võimalik mitme faili korraga nimetamiseks kasutada "?" tähenduses "täpselt üks tundmatu märk" ja "*" tähenduses "mistahes arv tundmatuid märke".
Teise näitena lubavad paljud tekstitöötlusprogrammid teksti otsimisel ja ka asendamisel kasutada mustrite kirjeldamiseks nn regulaaravaldisi (ingl regular expression).
Sellised vahendid võimaldavad aega kokku hoida, sest nii saab käske rakendada korraga paljudele failidele või sõnadele. Ilma nendeta tuleks käsk anda kas iga faili või iga võimaliku sõna kohta eraldi.

Kobras Brunol on arvutustabelis andmed ja valemid.

Nüüd hakkab ta valemitega arvutatud väärtustest (real 3) diagramme joonistama.
Millist allolevatest diagrammidest ta nende andmete põhjal kindlasti ei saa?
[Raadionupud]
A. 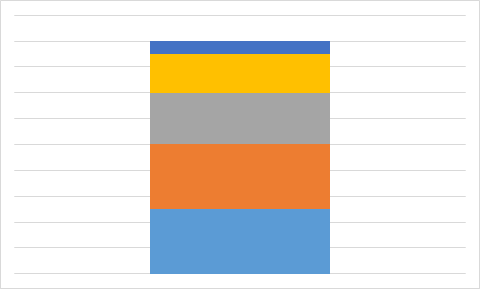
B. 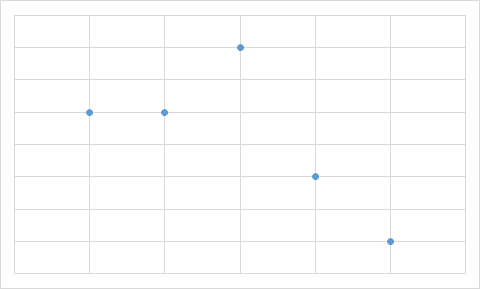
C. 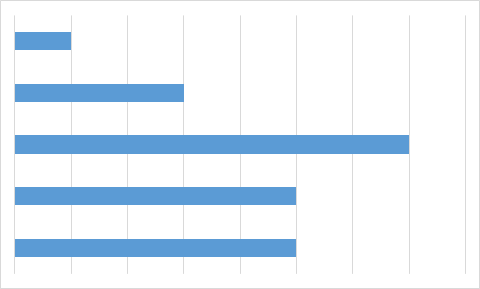
D. 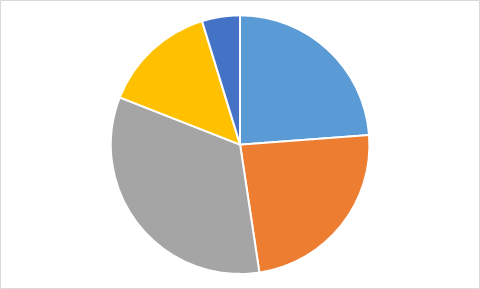
Õige vastus on: A.
Vastuse leidmiseks pole isegi vaja kõigi valemilahtrite väärtusi välja arvutada. Piisab tähelepanekust, et kolmel diagrammil on üks väärtus kõige suurem ja selle järel suuruselt teisi väärtusi kaks võrdset, aga diagrammil A on just maksimaalse suurusega väärtusi kaks võrdset. Seega ei ole diagramm A kindlasti koostatud samadest andmetest, millest ülejäänud.
Andmete töötlemisel võib kergesti juhtuda, et midagi läheb valesti. Sellepärast on alati kasulik oma töö tulemusele peale vaadata ja mõelda, kas seal on midagi, mis ilmselgelt ei klapi või ei sobi.

Koprakülas elab tosin perekonda. Arvutiteadlane Jeffrey koostas külaelanike kohta andmebaasi.

Ta salvestas iga külaelaniku andmed järgmise 16-bitise jadana (kus bitid on nummerdatud 0..15 paremalt vasakule):
| Bitid | Tähendus |
|---|---|
| b15..b12 | neli bitti perekonna järjekorranumbriks |
| b11 | üks bitt soo märkimiseks: 0 = emane; 1 = isane |
| b10..b4 | seitse bitti kehakaaluks (täisarv) |
| b3..b2 | kaks bitti ameti tähistamiseks: 00 = pesaehitaja; 01 = tammiehitaja; 10 = toiduvaruja; 11 = õpetaja |
| b1..b0 | kaks bitti lemmiktoidu tähistamiseks: 00 = puukoor; 01 = vetikad; 10 = kõrrelised; 11 = laugulised |
Näiteks bitijada 0100 0 0100101 10 01 (kus tühikud on loetavuse parandamiseks) tähistab kobrast, kes kuulub perekonda number 4, on emane, kelle kaal on 37 ja kes töötab toiduvarujana ning armastab vetikaid.
Jeffrey esitab andmebaasi päringuid loogiliste avaldistena, kus bittide väärtusi tõlgendatakse järgmiselt: 0 = väär; 1 = tõene.
Millised koprad vastavad järgmisele avaldisele?
b11 JA MITTE(b10) JA b9 JA b7 JA MITTE(b3 JA b2)
[Raadionupud]
A. Emased, kelle kaal on vähemalt 16 ja kes töötavad toiduvarujatena
B. Isased, kelle kaal on vähemalt 64 ja kes töötavad pesa- või tammiehitajatena
C. Isased, kelle kaal on 40 kuni 63 ja kes töötavad pesa- või tammiehitajate või toiduvarujatena
D. Isased, kelle kaal kuni 39 ja kes töötavad tammiehitajatena
Õige vastus on: C (isased, kelle kaal on 40 kuni 63 ja kes töötavad pesa- või tammiehitajate või toiduvarujatena).
Õige vastus on C, sest
Variant A ei saa olla õige, sest räägib emastest kobrastest, aga b11 = 1 tähendab "isane". Sellele variandile vastav avaldis oleks MITTE(b11) JA b8 JA b3 JA MITTE(b2).
Variant B ei saa olla õige, sest räägib kaalust vähemalt 64, aga b10 = 0 tähendab "kaal on alla 64". Sellele variandile vastav avaldis oleks b11 JA b10 JA MITTE(b3).
Variant C ei saa olla õige, sest räägib kaalust kuni 39, aga b9 = 1 ja b7 = 1 tähendab "kaal on vähemalt 32+8=40". Sellele variandile vastav avaldis oleks päris keeruline: b11 JA MITTE(b10) JA MITTE(b9 JA b8) JA MITTE(b9 JA b7) JA MITTE(b3) JA b2.
Arvuti mälus kodeeritakse kõik andmed bittidena ja elektroonika tasemel toimuvad kõik operatsioonid, sealhulgas ka arvude võrdlemised, bitiloogika tehetena. Kasutajate eest on see keerukus tavaliselt varjatud, sest sõltuvalt operatsiooni liigist ja protsessori tüübist teeb kasutajale nähtavate operatsioonide teisendamise bitiloogika teheteks ära kas rakendustarkvara, süsteemitarkvara või protsessor ise.
Programmi- ja päringukeeltes on lisaks JA (ingl AND) ja MITTE (ingl NOT) tehetele tavaliselt võimalik kasutada veel VÕI (ingl OR) ja sageli ka "välistav VÕI" (ingl exclusive OR, XOR) tehteid. Need lisatehted teevad mõnede loogiliste avaldiste kirjutamise mugavamaks, aga pole rangelt võttes vajalikud, sest kõik avaldised saab kirja panna ka ainult JA ja MITTE kombinatsioonidena.
Enamgi veel, tegelikult pole vaja isegi kahte erinevat tehet. On võimalik näidata, et kõik loogilised avaldised saab kirja panna ainult NING-EI (ingl NOT-AND, NAND) tehte abil, kus x NING-EI y = MITTE(x JA y). Selle kohta öeldakse, et NING-EI on universaalne tehe. Samamoodi on universaalne tehe ka VÕI-EI (ingl NOT-OR, NOR), kus x VÕI-EI y = MITTE(x VÕI y). Paljud elektroonikaskeemid koosnevadki ainult NING-EI elementidest, sest neid on pooljuhtidest väga lihtne moodustada.
Kopraküla teadlase Jeffrey nimi viitab USA arvutiteadlasele Jeffrey Ullmanile, kes on muude arvutiteaduse valdkondade kõrval andnud olulise panuse ka andmebaasisüsteemide alasesse uurimistöösse.

Kolamid on dekoratiivsed mustrid, mida saab põrandale joonistada näiteks kriidiga. Kolami joonistamiseks märgitakse kõigepealt ära mõned punktid ja seejärel tõmmatakse nende ümber jooned. Iga joont alustatakse ja lõpetatakse samas punktis, joonistamise ajal kriiti üles ei tõsteta.
Joon võib ristuda teiste joonte või iseendaga, kuid ei tohi teise joonega kattuda või seda isegi puutuda ilma sellega ristumata. Iga joon peab olema joonistatud vähemalt ühe punkti ümber. Iga sellisel viisil joonistatud joont nimetatakse silmuseks.
Allpool illustreeritud kolamil on 6 silmust. Pange tähele, et silmused ristuvad erinevates kohtades ja musta värvi silmus ristub ka iseendaga.
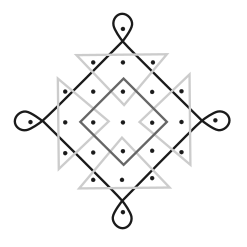
Millisel järgnevatest kolamitest on kõige vähem silmuseid?
[Raadionupud]
A. 
B. 
C. 
D. 
Õige vastus on: D.
Variandil A on 4 silmust:
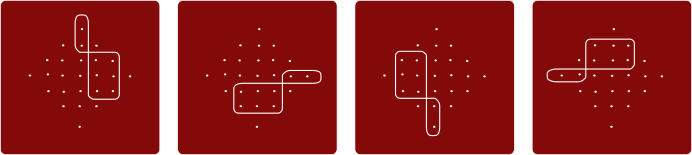
Variandil B on 5 silmust:

Variandil C on 3 silmust:
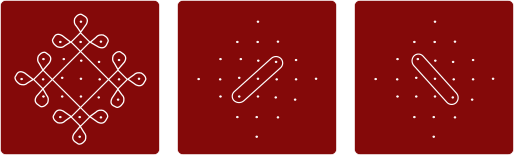
Variandil D on ainult üks silmus; ülevaatlikuse huvides näitame selle joonistamist etappide kaupa:

Kolamid on keerulised mustrid, mida leidub India linnades ja külades. Kuidas neid mustreid mäletatakse ja joonistatakse? Üks teooria on, et neid luuakse lihtsate reeglite järgi, mida antakse edasi põlvest põlve.
Reeglikogumite järgi neile vastavate tekstide genereerimist uuritakse arvutiteaduses formaalsete keelte teoorias. Kuigi genereerivad grammatikad mõeldi algselt välja tekstide (ühemõõtmeliste märgijadade) kirjeldamiseks, on hiljem seda ideed laiendatud ka mitmemõõtmelistele objektidele, sealhulgas ka graafilistele kujunditele. Selliseid meetodeid kasutatakse sageli ka generatiivses kunstis (ingl generative art).

Vaatame 6x5 ruudust koosnevat pilti, mille osad ruudud on mustad, osad valged:
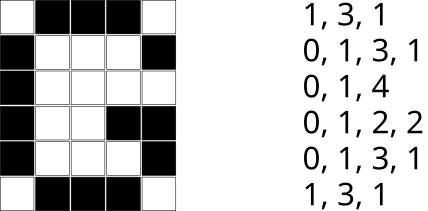
Selle pildi saab teisendada arvujadaks, lugedes iga rea puhul üle, mitu järjestikust ruutu on valged, seejärel mitu järjestikust ruutu on mustad, siis mitu järjestikust ruutu on valged jne, kuni jõuame rea lõppu. Pane tähele, et kui rida algab musta ruuduga, siis on selle rea alguses olevate valgete ruutude arv 0.
Lõpuks ühendame kõigi pildiridade kõik arvud ühte jadasse. Eeltoodud näites oleks tulemuseks selline jada: 1, 3, 1, 0, 1, 3, 1, 0, 1, 4, 0, 1, 2, 2, 0, 1, 3, 1, 1, 3, 1.
Milline 6x5 ruudust koosnev pilt oleks kujutatud jadaga 1, 4, 0, 1, 4, 1, 3, 1, 4, 1, 0, 1, 3, 1, 1, 3, 1?
[Raadionupud]
A. 
B. 
C. 
D. 
Õige vastus on: D.
Lahendamisel me saame järgida etteantud jada, joonistades selle järgi 6x5 maatriksi. Kui rida on täidetud, peame liikuma järgmisese ritta, alustades seal jälle valge värviga.
Alloleval pildil on näidatud õige vastus. Lisaks on näidatud, kuidas jada ridade kaupa tükkideks jagada.
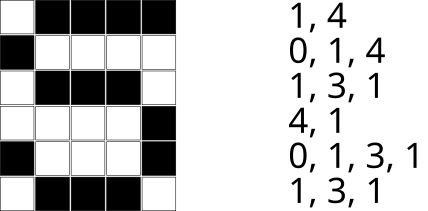
Variant A on vale, kuna selle jada oleks 0, 4, 1, 1, 1, 3, 1, 1, 3, 1, 1, 1, 2, 1, 1, 2, 1, 2, 2, 1.
Variant B on vale, kuna selle jada oleks 1, 4, 4, 1, 1, 3, 1, 0, 1, 4, 0, 1, 3, 1, 1, 3, 1.
Variant C on vale, kuna selle jada oleks 1, 4, 0, 1, 4, 0, 1, 3, 1, 4, 1, 0, 1, 3, 1, 1, 3, 1. Tasub mainimist, et selle pildi jada oleks otsitav 1, 4, 0, 1, 4, 1, 3, 1, 4, 1, 0, 1, 3, 1, 1, 3, 1, kui me ei alustaks kodeerimisel iga rea algusest uuesti valge värviga, vaid loendaks ridade vahetumisele vaatamata alati kordamööda valgeid ja musti ruute.
Piltide salvestamiseks või edastamiseks elektroonikaseadmete vahel on vaja need arvudeks teisendada. Selleks on palju viise ja siin on toodud neist üks. Kasutades ühte arvu sama värvi ruutude jada esitamiseks, tihendab see meetod andmeid ehk vähendab andmete hulka ja see on informaatikas oluline. Seda meetodit saab täiustada mitmel viisil, näiteks lubades arvul viidata rohkem kui ühte rida hõlmavale ruutude jadale.
Andmete esitamise viiside leidmine on olnud väljakutse alates juba esimestest elektroonilistest seadmetest, sest sellega seotud valikud võivad mõjutada teabe töötlemiseks või saatmiseks ja vastuvõtmiseks kuluvat aega. Praegu on see probleem endiselt aktuaalne, eriti internetis: uute viiside loomine piltide, videote ja muude meediumifailide kodeerimiseks võib meie veebikasutamist kiirendada.
Selles ülesandes kirjeldatud meetodit kasutasid vanad faksiaparaadid dokumentide sisu edastamiseks.
Copyright © 2022 Bebras – International Challenge on Informatics and Computational Thinking.
Licensed under Creative Commons Attribution-ShareAlike 4.0 International License.
Flag icons by GoSquared.