

Вероника очень любит прыгать. Она нашла 17 квадратов, расположенных на одной линии, и составила из них план прохождения дорожки.
Вероника положила монету на один конец дорожки из квадратов, а сама встала на другой конец дорожки лицом к монете.
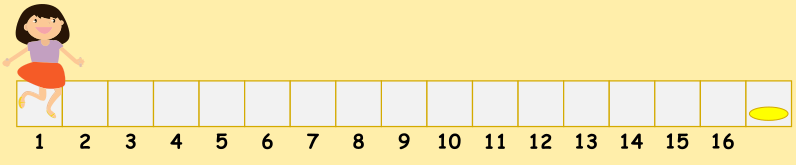
Она хочет прыгнуть на каждый квадрат дорожки, следуя правилам:
Цель игры — это, следуя правилам, добраться до монеты и при этом посетить все остальные квадраты.
Какие квадраты должны быть для этого отмечены "О"?
(Запишите через пробел числа в порядке возрастания, например, 2 6 12 15.)
[Tekstikast]
Правильный ответ: 3 4 7 8 11 12 15 16.
Порядок прыжков отмечен стрелками.
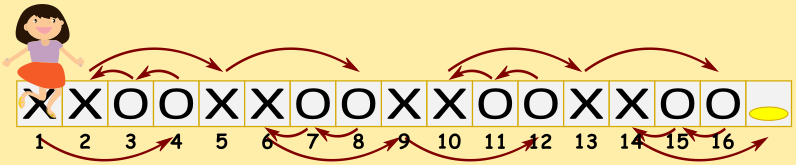
Посколько один прыжок позволяет вернуться только на один квадрат назад, у этого задания есть только одно решение. Если бы Вероника прыгнула вперёд более двух раз подряд, то она бы пропустила некоторые квадраты слева и уже не смогла бы вернуться к ним.
Нахождение последовательности действий для достижения цели по заранее заданным правилам называется алгоритмизацией. Робот или компьютерное приложение можно запрограммировать на работу в соответствии с заранее определёнными правилами. Если в результате нам нужен конкретный выход, то мы должны также указать соответствующий ввод. Допустим, у нас есть длинный узкий коридор в форме буквы L, и наш робот-пылесос может передвигаться только прямо и поворачивать на 90° вправо. Следовательно, нам нужно поставить его в конце более короткой части буквы L, иначе робот не сможет пропылесосить весь коридор.

Необходимо составить десятизначное число, используя каждую цифру (0–9) только один раз. Полученное число должно быть наименьшим, которое удовлетворяло бы всем следующим условиям:
0→9, 1→0, 1→2, 1→6, 2→3, 3→5, 3→4, 6→5, 5→7, 7→8, 9→7.
Условие a→b означает, что в составляемом десятизначном числе цифра a должна располагаться левее цифры b.
Какое наименьшее десятизначное число, в котором каждая цифра используется только один раз, удовлетворяет заданным условиям?
[Täisarv]
Правильный ответ: 1023465978.
Как же мы можем достоверно определить это число? Представим условия в виде графа, где его вершины содержат цифры, а между вершинами в соответствии с заданными условиями расположены направленные рёбра (дуги).
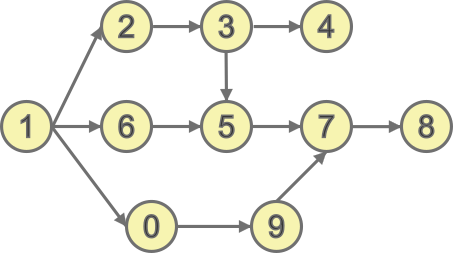
Искомое число должно начинаться с цифры, у которой нет входящей стрелки: тогда нет условия, требующего, чтобы некоторая другая цифра была слева от неё. Итак, составим искомое число, используя нижеприведённый алгоритм.
Пока имеются неиспользованные цифры, повторяем следующие шаги:
При выполнении этого алгоритма вершины графа проходятся в порядке, указанном красными числами. Таким образом, алгоритм дает нам искомое число 1023465978.
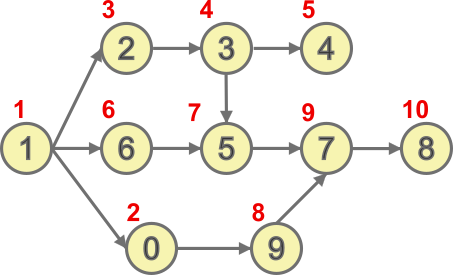
В этом задании нам дали только часть информации о том, как в искомом числе должны располагаться цифры, хотя указали, что необходимо составить число как полную последовательность цифр. В математике полная упорядоченность объектов (числовых или других), которая удовлетворяет некоторому условию частичной упорядоченности, называется топологической сортировкой этих объектов (англ topological sorting). Использованный при объяснении ответа алгоритм представляет собой стандартный метод нахождения топологической последовательности или обнаружения ее невозможности. Вы догадываетесь, почему невозможно составить число, которое удовлетворяло бы условиям 2→4, 4→3, 3→2?

Маленький бобр находится в лабиринте, который состоит из двух этажей. Планы этажей разные.
Бобр может переместиться со своего местоположения в соседнюю находящуюся на этом же этаже клетку, если между клетками нет стены. Каждое такое перемещение занимает одну секунду. С помощью магического жезла бобр также может переместиться в клетку, расположенную на том же месте, но уже на другом этаже. Однако такое перемещение занимает пять секунд.
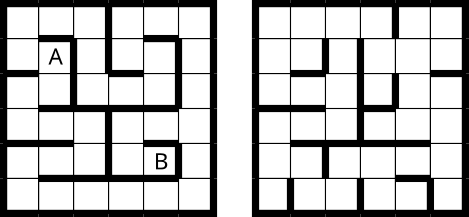
Например, если бобр находится в клетке A, то у него есть три возможных хода:
Бобр находится в клетке А и как можно быстрее хочет добраться до клетки B.
За какое наименьшее время бобр сможет добраться из клетки А в клетку В?
[Raadionupud]
A. За 16 секунд
B. За 17 секунд
C. За 18 секунд
D. За 20 секунд
Правильный ответ: C (за 18 секунд).
Это задание на нахождение наикратчайшего пути. Существуют разные подходы к поиску решения, одним из которых является так называемый алгоритм Дейкстры (англ Dijkstra's algorithm). Этот алгоритм позволяет находить наикратчайшие пути от заданной первоначальной клетки ко всем остальным клеткам.
На нижеприведённом рисунке показаны расстояния (длины наикратчайших путей) до всех клеток от клетки A.
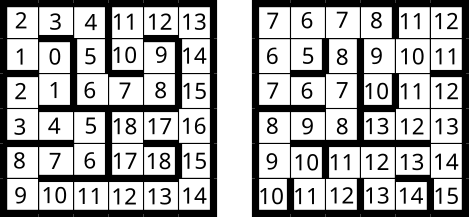
Мы можем заметить, что расстояние до клетки B равно 18. Один из возможных оптимальных путей таков:
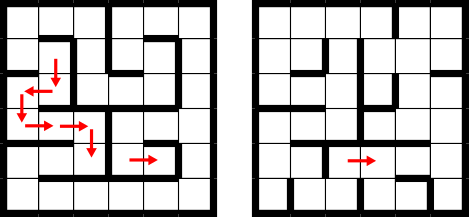
Ответ D (20 секунд) соответствовал бы оптимальному пути, если бы бобр двигался только в пределах одного этажа.
Поиск наикратчайшего пути — это стандартная задача теории графов. Возможности его применения включают поиск оптимального пути на карте города или в компьютерной сети, а также создание соединений в микросхемах. В нашем задании перемещение между этажами занимает больше времени, чем перемещение внутри одного этажа (5 и 1 секунда, соответственно). Также и в многослойных микросхемах соединения между слоями обходятся дороже, чем соединения внутри одного слоя. Сегодняшние VLSI-микросхемы используют 10-слойные кремниевые кристаллы, тогда как в нашем задании было всего два этажа. Кроме того, создание микросхем требует создания миллионов и миллиардов соединений.

Шесть бобров живут в разных частях Бобруйска. Они воспользовались метро, чтобы встретиться на одной из основных станций A, B, C или D. Бобры начали своё путешествие одновременно с разных станций и хотят добраться до места встречи как можно скорее.
На карте метро показаны имеющиеся на каждой линии станции (красные кружки) и время в минутах, необходимое для перемещения между ними. Кроме того, остановка на каждой станции занимает ещё одну минуту.
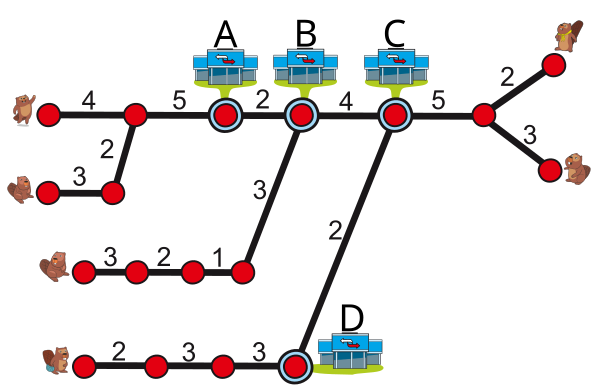
На какой станции должны встретиться друзья, чтобы как можно скорее увидеть друг друга?
[Raadionupud]
A. На станции A
B. На станции B
C. На станции C
D. На станции D
Правильный ответ: B (на станции B).
Чтобы решить это задание, нам нужно вычислить, сколько минут в пути был каждый бобр, при этом мы должны начать с его начальной станции и закончить каждой станцией A, B, C, D. Это, конечно, можно сделать, вычислив для каждого друга все возможные варианты времени в пути и посмотрев, сколько времени потребуется последнему другу, чтобы добраться до каждой станции. Но это было бы очень утомительной и долгой работой.
Для решения этого задания мы можем воспользоваться декомпозицией (разбивая задание на более мелкие части) и абстракцией (решая, какие маршруты важны для вычислений, а какие мы можем проигнорировать). Нам следует учитывать наибольшее время в пути по каждому маршруту, потому что нам нужно знать, сколько времени потребуется, чтобы до места встречи добрался последний друг.
Ниже мы покажем одну из возможных последовательностей шагов для решения этого задания.
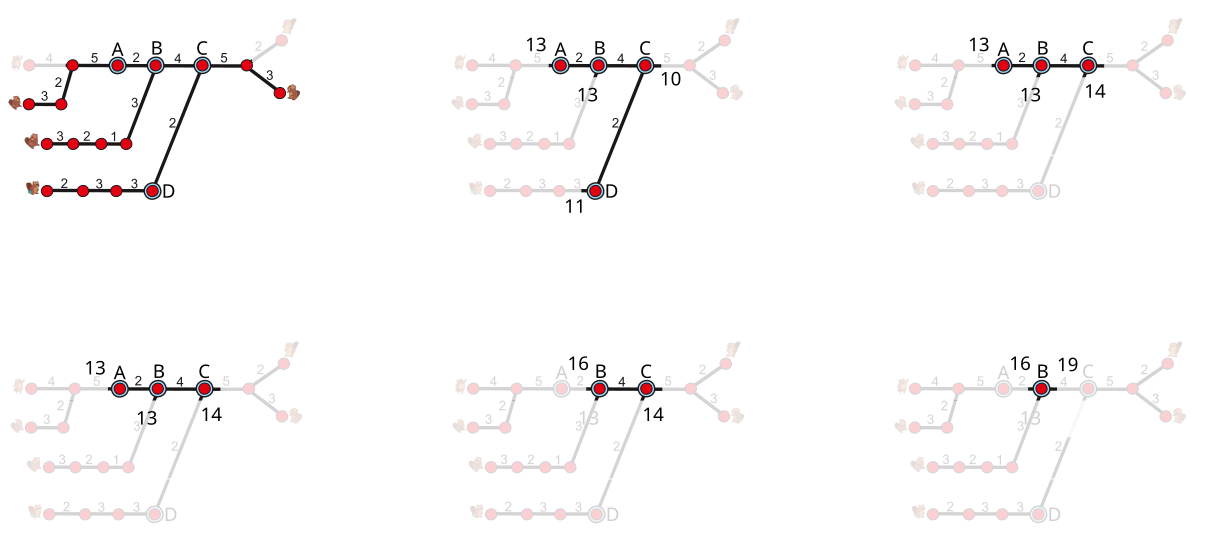
Рассматривая на плане возможности добраться до станции А для двух друзей слева, мы обнаружим, что первому другу для этого потребуется 11 минут (1+4+1+5), а второму — 13 минут (1+3+1+2+1+5). Что касается маршрута этих двух друзей отсюда к станциям B, C и D, то нам нужно принять во внимание только более длинное время прибытия, т.е. 13 минут. Точно так же и в случае двоих друзей справа, которые могли бы встретиться на станции C через 10 минут (1+3+1+5). Однако третьему другу (внизу плана) нужно 14 (1+2+1+3+1+3+1+2) минут, чтобы добраться до станции C. Значит, чтобы двигаться отсюда дальше, нам нужно учесть только 14 минут.
Продолжим рассуждать аналогично и в случае других станций (см. рисунок выше), всегда учитывая только самое длинное время прибытия, пока не достигнем конечной станции B. Это лучшая станция, куда все друзья могут добраться за самое короткое время, то есть за 19 минут.
Чтобы подтвердить наш результат, в приведённой ниже таблице показано, сколько минут потребуется друзьям, чтобы добраться до каждой станции с каждого направления. Сравнивая станции, мы можем заметить, что последний друг прибывает на станцию А за 22 минуты, на станцию В — за 19 минут, на станцию С — за 21 минуту и на станцию D — за 24 минуты. Это подтверждает, что станция B — лучшая станция для встречи.
| Время в пути до станции A | Время в пути до станции B | Время в пути до станции C | Время в пути до станции D |
|---|---|---|---|
| Слева: 13 | Слева: 16 | Слева: 21 | Слева: 24 |
| Справа: 22 | Справа: 19 | Справа: 10 | Справа: 11 |
В информатике динамическое программирование (англ dynamic programming) означает упрощение сложной задачи путём её разделения на более простые подзадачи. Такой подход часто используется в задачах оптимизации, где необходимо найти в некотором смысле наилучший (обычно наибольший или наименьший) вариант из всех возможных.
Использованный в этом задании рисунок называется графом (англ graph), его вершины (англ vertex) — это станции, а рёбра (англ edge) — это соединяющие их пути. Настоящий пример представляет собой взвешенный граф (англ weighted graph), потому что рёбрам присваиваются значения (время в пути). При моделировании задачи с помощью взвешенного графа, вес может обозначать такие параметры, как стоимость, длина, тяжесть или вместимость.


Бобр пошёл собирать яблоки и набрал в общей сложности 31 яблоко. Он хочет разложить их для хранения по пяти ящикам.

Бобр хочет, чтобы в дальнейшем он мог бы взять любое количество яблок, выбрав из имеющихся пяти ящиков один или несколько ящиков с яблоками и взяв из выбранных ящиков все яблоки.
Сколько яблок бобр должен положить в каждый ящик?
[Raadionupud]
A. 1, 3, 6, 9, 12
B. 1, 2, 4, 8, 16
C. 6, 6, 6, 6, 7
D. 1, 2, 3, 4, 5
Правильный ответ: B (1, 2, 4, 8, 16).
При поиске ответа мы должны следить, чтобы при сложении имеющегося в ящиках количества яблок, мы могли бы получить любое число от 1 до 31.
Поскольку нам нужна возможность взять одно яблоко, мы можем начать с того, что положим одно яблоко в первый ящик. Также нам нужна возможность получить два яблока — для этого мы можем положить два яблока во второй ящик. На данный момент мы можем взять одно (выбирая первый ящик), два (выбирая второй ящик) или три яблока (выбирая и первый, и второй ящики).
Следующее число, которое нам нужно получить, — это четыре. Для этого мы можем положить четыре яблока в третий ящик. Теперь мы можем взять одно, два, три (как и раньше), четыре (выбирая третий ящик), пять (выбирая первый и третий ящики), шесть (выбирая второй и третий ящики) и семь яблок (выбирая первый, вторый и третий ящики). Продолжая в том же духе, мы придем к решению, при котором в первом ящике находится одно яблоко, во втором два, в третьем четыре, в четвёртом восемь и в последнем шестнадцать яблок. Теперь мы можем взять любое количество яблок (от 1 до 31), выбрав определённое количество ящиков из наших пяти ящиков.
Вариант А неверен, потому что у нас нет такого комплекта ящиков, в которых было бы, например, всего два или пять яблок.
Вариант C также неверен, потому что мы не сможем взять меньше шести яблок.
Вариант D также неверен, потому что мы не сможем взять более 15 яблок. В данном случае бобр даже не положил все свои яблоки в ящики!
Это задание связано с двоичной системой счисления (англ binary numeral system), которая является наиболее распространенной используемой в компьютерах системой счисления. Как вы можете видеть в решении, мы использовали степени числа 2 (1, 2, 4, 8, 16), чтобы представить любое число от 1 до 31 (на самом деле даже от 0 до 31, потому что также существует возможность не взять ни одного ящика и не получить ни одного яблока). Это похоже на компьютер, который работает только с числами, которые могут быть представлены 5 двоичными цифрами (5 битами):
| Бит | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Показатель степени (p) | 0 | 1 | 2 | 3 | 4 |
| 2p | 1 | 2 | 4 | 8 | 16 |
Для решения нашего задания именно числа в последней строчке (2p) укажут нам количество яблок в каждом ящике.

Международные Бобровые игры — это ежегодное соревнование, которое состоит из трёх туров. В начале все 8 участников образуют одну команду. В каждом туре каждая команда делится пополам по жребию, и далее половинки соревнуются друг против другом. Таким образом, первый и второй туры — командные, а последний тур является индивидуальным. Каждое соревнование выигрывает та команда, сумма баллов всех участников которой была больше. Абсолютным победителем игр становится тот, кто выигрывает все три тура подряд. В этом году счастливым абсолютным победителем Бобровых игр стала бобр Анна.
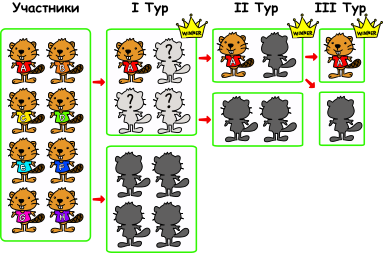
В таблице показаны баллы, заработанные всеми участниками в каждом туре. Имена участников записаны по-английски, чтобы помочь судьям избежать путаницы в написании иностранных имён.
| Тур | Anna  |
Bruno  |
Carolin  |
Daisi  |
Eero  |
Feliks  |
Georg  |
Helen  |
|---|---|---|---|---|---|---|---|---|
| 1ый тур | 15 | 16 | 19 | 18 | 17 | 20 | 19 | 19 |
| 2ой тур | 20 | 27 | 30 | 24 | 28 | 24 | 30 | 30 |
| 3ий тур | 10 | 14 | 11 | 15 | 16 | 13 | 9 | 12 |
Какие три бобра были в первой команде бобра Anna?
[Märkeruudud]
B. Bruno
C. Carolin
D. Daisi
E. Eero
F. Feliks
G. Georg
H. Helen
Правильный ответ: D, F, G (Daisi, Feliks и Georg).
Третий тур — индивидуальный. Поскольку бобр Georg — это единственный игрок, у которого меньше баллов, чем у бобра Anna, то они должны были встретиться в третьем туре, а во втором туре оказаться в одной команде.
Сумма баллов у бобров Anna и Georg во втором туре равна 50. Эта сумма должна быть больше, чем сумма баллов другой команды, состоящей из двух бобров. Бобры Daisi и Feliks — единственные, у кого сумма баллов меньше 50 очков. Поэтому в первом туре они должны были быть в одной команде с бобрами Anna и Georg. Теперь мы знаем кто был в команде, а значит у нас есть ответ.
Но в качестве проверки мы всё же посчитаем:
Значит, бобр Anna действительно является абсолютным победителем международных Бобровых игр 2023.
Если мы попытаемся решить это задание от начала в направлении конца (а не с конца), то потребуется перебор многих возможных комбинаций и оценка результатов нескольких туров для каждой комбинации. Это займёт много времени.
В таких случаях информатики ищут более эффективные методы решения задания. В данном случае подход к решению задания с конца в направлении начала очень быстро даст нам правильное решение, как и было показано выше.
Этот метод используется в ситуациях, когда ищется решение, которое должно удовлетворять определённым ограничениям. В некоторых случаях для поиска решения комбинируется прямой и обратный поиски.

На каждой вершине восьмиугольника записаны три или четыре буквы. Исходящая из центра восьмиугольника чёрная стрелка указывает на некоторую группу букв. Стрелка может вращаться только по движению часовой стрелки.
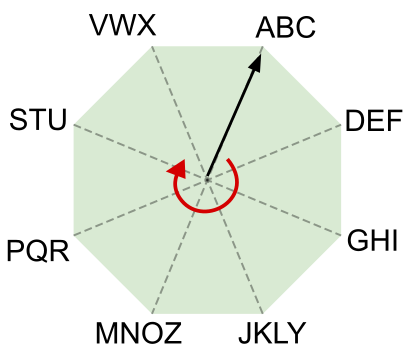
Воспользуемся этими восьмиугольником и стрелкой для кодирования сообщений. В начале кодирования нового сообщения стрелка указывает на группу букв ABC. Далее кодируем каждую букву сообщения следующим образом:
Например, сообщение "TREE" будет закодировано с помощью последовательности 62-73-42-02.
Как будет закодировано сообщение "WATER"?
(Запишите пары чисел, разделяя их тире, например, 12-23-34-45-56.)
[Tekstikast]
Правильный ответ: 72-11-62-32-43.
Мы получим правильный ответ, если закодируем сообщение "WATER" по буквам. Код сообщения содержит 5 пар цифр:
Таким образом, код сообщения 72-11-62-32-43.
Одним из методов защиты данных от посторонних лиц является шифрование. Наука о шифрах или криптография (англ cryptography) появилась уже 3500 лет назад. Один из самых простых шифров — это замена каждой буквы на другую букву. Такой т.н. шифр подстановки (англ substitution cipher) легко взломать, потому что частотность разных букв в каждом языке своя, и на основе этой частотности можно довольно легко найти коды наиболее часто используемых букв.
В нашем задании используется метод, который за счёт вращения стрелки даёт разные коды для одной и той же буквы — в зависимости от того, какая буква была предыдущей в сообщении. Благодаря этому создаётся некоторая изменчивость, вариативность, в шифре и это затрудняет его взлом. Однако шифр достаточно прост, чтобы его можно было легко запомнить.
Если бы мы разделили буквы на группы по-другому или расположили группы в вершинах восьмиугольника в другом порядке, то мы бы получили разные коды для одного и того же сообщения. Такая настройка схемы шифрования называется ключом шифрования (англ encryption key), а его угадывание — криптоанализом (англ cryptoanalysis).

В классе имеется 31 стул. Они расположены по кругу и пронумерованы от 1 до 31, как показано на рисунке.
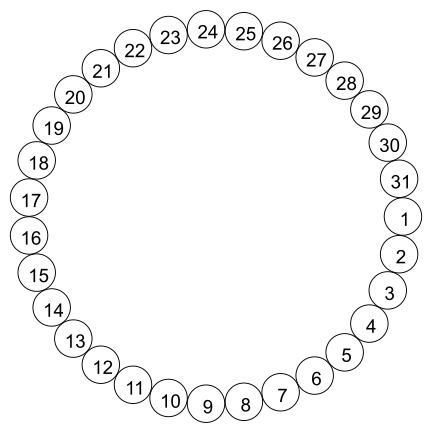
Дети играют в игру по следующим правилам:
Допустим, что Катя и Маша — близнецы, родившиеся 20 апреля, Тимур родился 21 января, а Толя — 22 сентября.
Они заходят в класс в следующем порядке: Катя, Маша, Толя, Тимур. Катя садится на 20ый стул, Маша на 21ый стул, Толя на 22ой стул, а Тимур на 23ый стул.
Если же дети заходят в класс в порядке Маша, Тимур, Толя, Катя, то Маша садится на 20ый стул, Тимур на 21ый стул, Толя на 22ой стул, а Катя на 23ый стул.
Шестеро учеников уже вошли в класс, и они сидят, как показано в таблице:
| Имя | День рождения | Номер стула |
|---|---|---|
| Аня | 11 мая | 13 |
| Боря | 12 февраля | 12 |
| Веня | 14 сентября | 14 |
| Гена | 11 августа | 11 |
| Диана | 13 апреля | 15 |
| Елена | 12 июля | 16 |
Какое из следующих утверждений не может быть верным?
[Raadionupud]
A. Веня сел первым
B. Елена села последней
C. Диана села раньше Ани
D. Боря сел раньше Гены
Правильный ответ: C (Диана села раньше Ани).
Веня сидит на стуле, номер которого соответствует дню его рождения. Значит, он мог зайти в класс первым, а вариант А может быть верным утверждением.
Чтобы сесть на стул под номером 16, Елена должна была зайти в класс после тех, кто уже сидит на стульях 12–15. Гена сидит на стуле 11, а это значит, что он должен был зайти раньше Ани, с которой у него один и тот же день рождения. Следовательно, вариант B — это верное утверждение.
Если бы Диана зашла раньше Ани, то стул под номером 13 был бы свободен, и Диане не пришлось бы садиться на стул под номером 15. Следовательно, вариант С не может быть верным утверждением.
Боря и Гена, оба сидят на стульях, номера которых соответствуют дням их рождения, и они могли зайти в класс всё равно в каком порядке. Таким образом, вариант D может быть верным утверждением.
Хэширование (англ hashing) — это метод разделения большого количества возможных входных значений на фиксированный набор выходных значений. В этом задании входным набором является набор всех дней рождения, а выходным набором — стулья с номерами от 1 до 31. Хеш-функция вычисляет выходное значение на основе каждого входа. Если входной набор больше выходного набора, то двум входным значениям может быть сопоставлено одно и то же выходное значение. Поэтому нам необходимо предложить механизм для разрешения таких столкновений (англ collision). Данное задание описывает решение, которое называется открытой адресацией, где в случае столкновений более позднее входное значение направляется на следующее значение выходного набора. Хеширование и его различные механизмы для разрешения столкновений используются при хранении данных в хеш-таблицах (англ hash table).

У Томаса есть коллекция драгоценных камней, где у каждого камня есть своя оценка по шкале предпочтений.
Сара знает, какие драгоценные камни есть в коллекции Томаса, но не знает, как они упорядочены по шкале предпочтений. Она хочет выяснить, какой драгоценный камень является самым любимым у Томаса.
Сара выбирает четыре драгоценных камня из коллекции Томаса и спрашивает его: "Какой из этих четырех камней твой любимый?". Далее Сара выбирает новый набор из четырёх драгоценных камней и снова задаёт этот же вопрос. Затем она выбирает третий набор, состоящий вновь из четырёх драгоценных камней, и задаёт свой вопрос в последний раз. (Некоторые драгоценные камни могут оказаться в более чем одном выбранном Сарой наборе.)
Каково наибольшее количество драгоценных камней может быть в коллекции Томаса, чтобы Сара смогла таким образом определить его самый любимый камень?
[Raadionupud]
A. 8 драгоценных камней
B. 10 драгоценных камней
C. 11 драгоценных камней
D. 12 драгоценных камней
Правильный ответ: B (10 драгоценных камней).
В случае с десятью драгоценными камнями Сара, задав два первых вопроса, сможет узнать о восьми различных драгоценных камнях. Любимый камень в каждом из наборов может оказаться самым любимым камнем Томаса во всей коллекции, а три оставшихся драгоценных камня из каждого набора не будут являться таковыми. Следовательно, Сара может задать третий и последний вопрос о наборе, который будет состоять из двух любимых камней из предыдущих наборов, о которых она уже успела спросить, и двух драгоценных камнях, о которых она ещё не успела спросить. Ответ Томаса на третий вопрос позволит ей выявить самый любимый камень Томаса.
Таким образом, мы показали, что у Сары есть стратегия, которая работает, если в коллекции имеется 10 драгоценных камней. (Есть и другие подобные стратегии.) Далее мы покажем, что не существует подходящей стратегии, если бы у Томаса в коллекции было больше драгоценных камней. Для этого предположим, что у Томаса есть как минимум 11 драгоценных камней, и сосредоточимся на первых двух вопросах Сары.
Если в этих наборах есть хотя бы один общий драгоценный камень, то после первых двух вопросов останутся не проанализированными ещё как минимум четыре камня. В этом случае Саре нужно будет спросить об этих четырёх непроанализированных драгоценных камнях, потому что, если она этого не сделает, один из них может оказаться самым любимым камнем Томаса. Теперь Сара, конечно, узнает, какой будет любимым камнем Томаса среди них, но она не сможет его сравнить с остальными семью уже проанализированными камнями. Таким образом, её стратегия не позволит определить, какой драгоценный камень является самым любимым камнем Томаса.
Если же в первых двух наборах Сары не будет общих драгоценных камней, то среди кандидатов останутся драгоценные камни, которые стали ответом на первые два вопроса Сары, и три оставшихся ещё не проанализированными камня. У Сары останется только один вопрос, и она не сможет выяснить, какой из пяти камней является любимым камнем Томаса.
Таким образом, мы показали, что у Сары не может быть стратегии, которая позволила бы задать три вопроса и выяснить самый любимый камень Томаса, если бы в коллекции было более 10 драгоценных камней.
Это задание связано с алгоритмами, у которых есть ограничения. Сара может задать только три вопроса, и каждый вопрос позволит ей узнать что-то только о четырёх драгоценных камнях. Из-за этих ограничений мы имеем алгоритм, который работает в случае, когда у нас имеется до 10 драгоценных камней, но не существует алгоритма, корректно работающего для большего количества камней.
На практике алгоритмы могут иметь различные ограничения по разным причинам. Например, алгоритм, управляющий аварийным торможением машины или устройства, должен обязательно среагировать до того, как машина кого-нибудь заденет. Системы управления таким оборудованием часто используют специальные так называемые операционные системы реального времени (англ real-time operating system, RTOS). Другим потенциальным источником ограничений является то, что некоторые операции могут быть очень дорогими. Например, требовать дорогостоящих вспомогательных материалов или износить дорогостоящего оборудования.
Если какой-то алгоритм работает корректно только в ограниченных условиях (например, в нашем задании Сара смогла найти самый любимый камень из максимум 10 драгоценных камней, используя три вопроса), то это не всегда является большим недостатком. Однако инженеры, применяющие алгоритмы в своей работе, должны знать об этих ограничениях и стараться не превышать эти ограничений при применении алгоритмов.

Шесть кусочков головоломки имеют одинаковую форму:

Выступы на каждом из этих кусочков идеально совпадают с выемками на других кусочках.
Следуй алгоритму:
Какая из нижеприведённых фигур не может быть создана, следуя этому алгоритму?
[Raadionupud]
A. 
B. 
C. 
D. 
Правильный ответ: D.
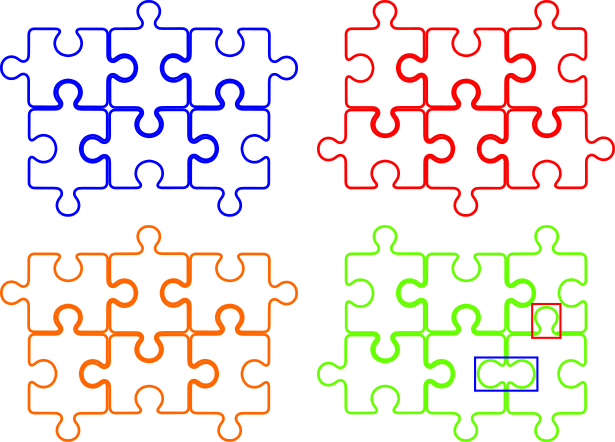
При создании алгоритма нас всегда должно интересовать, в каком состоянии он окажется. Если мы действительно понимаем работу алгоритм, то мы часто можем предсказать конечное состояние без выполнения всех шагов. Если мы найдём какой-то символ или атрибут, который при выполнении алгоритма в разных решениях по-разному меняется, то мы можем использовать его для поиска правильного решения.

Бобр Марк ищет номер телефона своего друга на очень длинной интернет-странице. Марк не уверен, как точно пишется имя друга, поэтому использует для поиска специальные символы:
| Символ | Значение |
|---|---|
| ? | точно одна неизвестная буква |
| & | точно две неизвестные буквы подряд |
| % | любое количество неизвестных букв до конца имени |
Например, поисковый запрос «Ma%» может выдать имена Maрия, Maрк и т.д.
Какие из следующих имён выдаст поисковый запрос «S?rah B&cht%»?
(Отметь все правильные ответы.)
[Märkeruudud]
A. Sarah Birchtree
B. Sara Benchton
C. Sarah Bilchman
D. Sirah Beachtram
Правильный ответ: A, D.
Вариант A правильный, потому что имя «Sarah Birchtree» соответствует поисковому запросу «S?rah B&cht%»:
Вариант B не может быть правильным, потому что в имени «Sara» отсутствует буква «h».
Вариант C не может быть правильным, потому что в фамилии «Bilchman» вместо «cht» имеется «chm».
Вариант D правильный, потому что буквы имени и фамилии соответствуют используемому запросу: «S» и «S», «i» и «?», «rah» и «rah», пробел и пробел, «B» и «B», «ea» и «&», «cht» и «cht», а также «ram» и «%».
Многие информационные системы позволяют использовать для поиска информации так называемые символы подстановки (англ wildcard) или символы-джокеры. Примером их использования были специальные символы, которые были описаны в этом задании. Также во многих командах Windows, MacOS и Linux для одновременного именования нескольких файлов можно использовать «?», что означает «только один неизвестный символ», и «*», что означает «любое количество неизвестных символов».
Другой пример: многие программы обработки текста позволяют использовать так называемые регулярные выражения (англ regular expression). Эти выражения позволяют описать шаблоны, которые используются для поиска или замены текста.
Такие инструменты позволяют сэкономить время, потому что команда может быть одновременно применена ко многим файлам или словам. Без них команду пришлось бы давать отдельно для каждого файла или каждого возможного слова.

У бобра Максима в электронной таблице есть данные и формулы.

Теперь на основании вычисленных по формулам значений (в строке 3) он строит диаграммы.
Какую из приведенных ниже диаграмм Максим никогда не получит на основании этих данных?
[Raadionupud]
A. 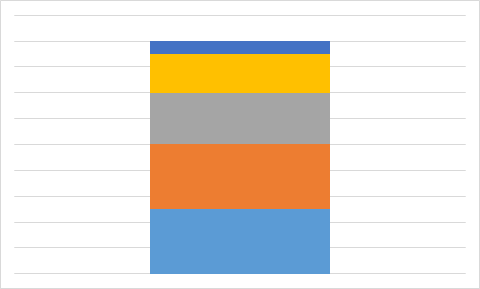
B. 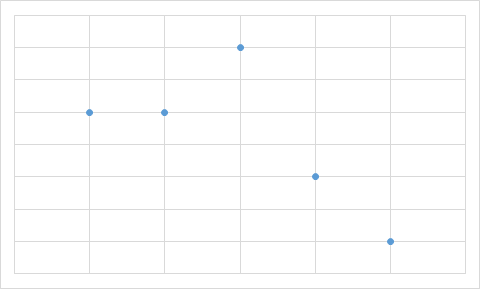
C. 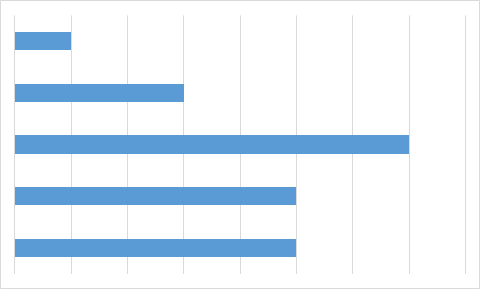
D. 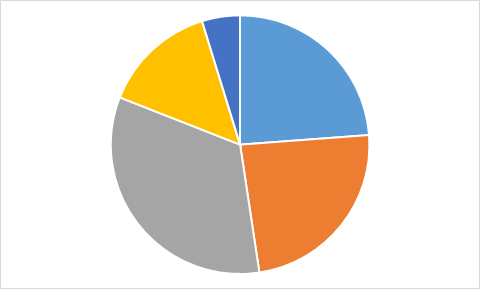
Правильный ответ: A.
Чтобы найти ответ, не нужно даже вычислять значения всех ячеек с формулами. Достаточно заметить, что на трёх диаграммах только одно значение является максимальным, а два следующих (по величине) значения — одинаковы. Однако на диаграмме А есть именно два равных максимальных значения. Поэтому диаграмма А определённо не составлена по тем же данным, что используются в остальных диаграммах.
При обработке данных может случиться так, что что-то случайно пойдёт не так. Именно поэтому всегда полезно посмотреть на результат своей работы и подумать, если там что-то такое, что явно не сходится или не подходит.

В Бобруйске проживает дюжина семей. Информатик Джеффри создал базу данных жителей этой деревни.

Он сохранил данные каждого жителя в виде 16-битной последовательности (биты пронумерованы 0..15 справа налево):
| Биты | Обозначение |
|---|---|
| b15..b12 | четыре бита для порядкового номера семьи |
| b11 | один бит для обозначения пола: 0 = самка; 1 = самец |
| b10..b4 | семь битов для обозначения веса (целое число) |
| b3..b2 | два бита для обозначения профессии: 00 = строитель нор; 01 = строитель плотин; 10 = повар; 11 = учитель |
| b1..b0 | два бита для обозначения любимого лакомства: 00 = кора дерева; 01 = водоросли; 10 = злаки; 11 = корешки |
Например, последовательность битов 0100 0 0100101 10 01 (пробелы представлены только для удобства чтения) описывает бобра, который принадлежит к семейству номер 4, является самкой весом 37, работает поваром и любит водоросли.
Джеффри с помощью логических выражений делает запрос в базу данных, где значения битов интерпретируются следующим образом: 0 = ложь; 1 = истина.
Какие бобры соответствуют следующему выражению?
b11 И НЕ(b10) И b9 И b7 И НЕ(b3 И b2)
[Raadionupud]
A. Самки, которые весят по меньшей мере 16 и работают поварами
B. Самцы, которые весят по меньшей мере 64 и работают строителями нор или строителями плотин
C. Самцы, чей вес находится в промежутке от 40 до 63, и которые работают или строителями нор, или строителями плотин, или поварами
D. Самцы, которые весят до 39 и работают строителями плотин
Правильный ответ: C (самцы, чей вес находится в промежутке от 40 до 63, и которые работают или строителями нор, или строителями плотин, или поварами).
Правильный ответ C, потому что
Вариант А не может быть правильным, потому что речь идет о самках, а b11 = 1 обозначает «самца». Выражение, которое бы соответствовало этому варианту, было бы НЕ(b11) И b8 И b3 И НЕ(b2).
Вариант B не может быть правильным, потому что в нём говорится о весе не менее 64, а b10 = 0 обозначает «вес меньше 64». Выражение, которое бы соответствовало этому варианту, было бы b11 И b10 И НЕ (b3).
Вариант C не может быть правильным, потому что в нём говорится о весе до 39, а b9 = 1 и b7 = 1 обозначает, что "вес не менее 32+8=40". Выражение, которое бы соответствовало этому варианту, было бы довольно сложным: b11 И НЕ(b10) И НЕ(b9 И b8 sub>) И НЕ(b9 И b7) И НЕ(b3) И b2 .
В памяти компьютера все данные кодируются с помощью битов, а на уровне электроники все операции, включая сравнение чисел, выполняются как битовые логические операции. Обычно эта сложность скрыта от пользователей, так как в зависимости от вида операции и типа процессора преобразования операции пользователя в битовую логику проводит либо прикладное программное обеспечение, либо системное программное обеспечение, либо сам процессор.
В языках программирования и запросов в дополнение к операциям И (англ AND) и НЕ (англ NOT) можно также использовать операции ИЛИ (англ OR), а также «исключающее ИЛИ» (англ exclusive OR, XOR). Эти дополнительные операции делают запись некоторых логических выражений более удобной, но, строго говоря, они не являются необходимыми, поскольку все выражения также могут быть записаны, используя только комбинации И и НЕ.
Более того, вам даже не нужно делать две разные операции. Можно показать, что все логические выражения можно записать только с помощью операции И-НЕ (англ NOT-AND, NAND), где х И-НЕ у = НЕ(х И у). По этому случаю говорят, И-НЕ — это универсальная операция. Точно так же универсальна операция ИЛИ-НЕ (англ NOT-OR, NOR), где x ИЛИ-НЕ y = НЕ(x ИЛИ y). Многие электронные схемы состоят только из элементов И-НЕ, потому что их очень легко собрать из полупроводников.
Имя информатика из Бобруйска — Джеффри — является отсылкой на учёного-информатика Джеффри Ульмана, который, помимо других областей информатики, также внёс значительный вклад в исследования систем баз данных.

Коламы — это декоративные узоры, которые можно нарисовать на полу, например, с помощью мела. Чтобы нарисовать колам, сначала отмечают несколько точек, а затем рисуют вокруг них линии. Каждая линия начинается и заканчивается в одной и той же точке, мел во время рисовании не отрывается от пола.
Линия может пересекать другие линии или саму себя, но не может совпадать или даже касаться другой линии, не пересекая её. Каждая линия должна быть нарисована вокруг хотя бы одной точки. Каждая линия, нарисованная таким образом, называется петлей.
Колам, показанный ниже, имеет 6 петель. Обратите внимание, что петли пересекаются в разных местах, а петля чёрного цвета также пересекает саму себя.
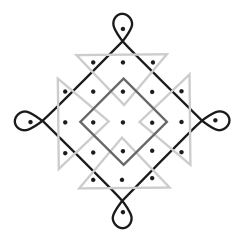
Какой из следующих коламов имеет наименьшее количество петель?
[Raadionupud]
A. 
B. 
C. 
D. 
Правильный ответ: D.
В варианте A имеется 4 петли:
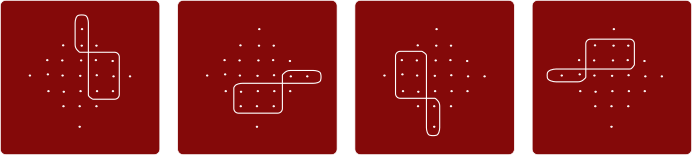
В варианте B имеется 5 петель:

В варианте C имеется 3 петли:
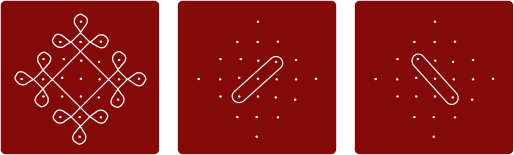
В варианте D только одна петля; для наглядности покажем, как нарисовать этот колам поэтапно:

Коламы — это замысловатые узоры, которые можно найти в индийских городах и деревнях. Как запоминаются и рисуются эти узоры? Одна из теорий гласит, что они создаются по простым правилам, которые передаются из поколения в поколение.
Генерация текстов, которые соответствуют наборам правил, изучается в информатике в рамках теории формальных языков. Хотя изначально генеративные грамматики были предназначены для описания текстов (представляющих из себя одномерные строки символов), позже эта идея была распространена на многомерные объекты, включая графические изображения. Такие методы также часто используются в процедуральном искусстве (англ generative art).

Рассмотрим изображение, состоящее из 6x5 квадратов, где некоторые квадраты чёрные, а некоторые — белые:
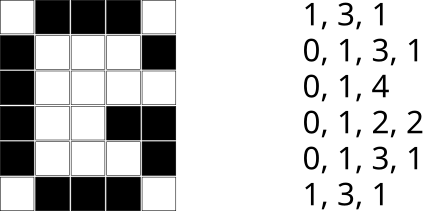
Это изображение можно преобразовать в последовательность чисел, подсчитав для каждой строки, сколько квадратов последовательно окрашено в белый цвет, а затем сколько квадратов последовательно окрашено в чёрный цвет, далее сколько квадратов последовательно окрашено в белый цвет и т.д., пока мы не достигнем конца строки. Обратите внимание, что если строка начинается с чёрного квадрата, то количество белых квадратов в начале этой строки равно 0.
В самом конце мы должны объединить все числа, которые получились для каждой строчки, в одну последовательность чисел. В случае вышеприведённого изображения получится следующая последовательность: 1, 3, 1, 0, 1, 3, 1, 0, 1, 4, 0, 1, 2, 2, 0, 1, 3, 1, 1, 3, 1.
Kакое изображение, состоящее из 6x5 квадратов, будет представлено последовательностью 1, 4, 0, 1, 4, 1, 3, 1, 4, 1, 0, 1, 3, 1, 1, 3, 1?
[Raadionupud]
A. 
B. 
C. 
D. 
Правильный ответ: D.
При решении мы можем следовать заданной последовательности, рисуя соответствующую матрицу 6x5. Когда строка заполнена, нам нужно перейти к следующей строке, начиная снова с белого цвета.
На нижеприведённом изображении показан правильный ответ. Также показано деление последовательности на фрагменты каждой строки.

Вариант A неправильный, потому что его последовательность была бы 0, 4, 1, 1, 1, 3, 1, 1, 3, 1, 1, 1, 2, 1, 1, 2, 1, 2, 2, 1.
Вариант B неправильный, потому что его последовательность была бы 1, 4, 4, 1, 1, 3, 1, 0, 1, 4, 0, 1, 3, 1, 1, 3, 1.
Вариант C неправильный, потому что его последовательность была бы 1, 4, 0, 1, 4, 0, 1, 3, 1, 4, 1, 0, 1, 3, 1, 1, 3, 1. Стоит отметить, что последовательность для этого изображения действительно была бы 1, 4, 0, 1, 4, 1, 3, 1, 4, 1, 0, 1, 3, 1, 1, 3, 1, если бы каждый раз мы не приступали к кодированию начала каждой строки с белого цвета, а использовали и считали бы попеременно то белые, то чёрные квадраты, переходя на следующую строку.
Для хранения или передачи изображений между электронными устройствами необходимо преобразовать их в числа. Есть много способов сделать это, и в этом задании показан один из них. Используя одно число для представления последовательности квадратов одного и того же цвета, этот метод сжимает данные, т.е. уменьшает объём данных, а это имеет важное значение в информатике. Этот метод можно улучшить несколькими способами, например, позволив числу ссылаться на последовательность, которая охватывает квадраты более чем одной строки.
Поиск способов представления данных был сложной задачей с момента появления первых электронных устройств. Выбор способа может повлиять на время, необходимое для обработки или отправки и получения информации. Сегодня эта проблема по-прежнему актуальна, особенно в Интернете: создание новых способов кодирования изображений, видео и других медиафайлов может ускорить нашу работу в Интернете.
Описанный в этом задании метод использовался старыми факсами для передачи содержания документов.
Copyright © 2022 Bebras – International Challenge on Informatics and Computational Thinking.
Licensed under Creative Commons Attribution-ShareAlike 4.0 International License.
Flag icons by GoSquared.