Daniel otsib aaret, mis on peidetud mänguvälja ühte ruutu. Ta alustab S-tähega märgitud ruudust ja võib igal sammul liikuda edasi samas reas või samas veerus olevasse naaberruutu. Iga sammu järel öeldakse talle, kas ta liikus aardele lähemale ("L") või sellest kaugemale ("K"). Aarde kaugus on vähim selleni jõudmiseks vajalike sammude arv.
Oletame näiteks, et 3x3 väljakul on aare peidetud tärniga ruutu ja Daniel astub S-tähega märgitud ruudust alustades kaks sammu allapoole. Siis on tema kaugus aardest igas ruudus selline, nagu näidatud alloleval joonisel paremal. Seega saab ta esimese sammu järel signaali "L" ja teise järel signaali "K", nagu näidatud joonisel vasakul:
Nüüd mängib Daniel 4x7 väljakul. Tema liikumine ja saadud signaalid on näidatud alloleval joonisel. Millises ruudus on aare?
[Interaktiivne]
(Klõpsa õigel ruudul; valiku muutmiseks klõpsa uuesti.)
Õige vastus on:
.
Tom elab külas, kus on ainult kuus maja (koos tema enda koduga). Küla omapära on, et kõik teerajad selles külas on ühepikkused.
Tom koostas kaardi, mis näitab lühimaid teid tema kodust kõigisse teistesse majadesse. Sellel kaardil ei tarvitse olla kõiki teeradasid, mis külas olemas on, sest Tom märkis kaardile ainult lühimad teed oma kodust teiste majade juurde.
Me ei tea, milline oleks küla kaart, kui sellele oleks märgitud kõik teerajad. Aga milline järgmistest see kindlasti olla ei saa?
[Raadionupud]
A. B.
C.
D.
Õige vastus on: C.
Kaubarongi igas vagunis on üks kast. Kastide tõstmiseks on üks kraana, mis seisab oma kohal ja ei liigu. Kasti tõstmiseks peab see olema täpselt kraana all.
Kastid on nummerdatud ja nad on vaja maha tõsta numbrite järjekorras, alustades kastist number 1. Rong saab sõita ainult edasi. Aga ta on ringteel ja võib vajaduse korral kraana alt ära sõita ja ringiga tagasi tulla.
Ülalolevas näites tuleb kastid maha tõsta järjekorras 1, 2, 3, 4. Esimesel ringil peab kraana kasti 4 vahele jätma, saab kasti 1 maha tõsta, peab kasti 3 vahele jätma ja saab kasti 2 maha tõsta. Teisel ringil peab kraana kasti 4 vahele jätma ja saab kasti 3 maha tõsta. Kolmandal ringil saab lõpuks ka kasti 4 maha tõsta.
Mitu ringi on vaja, et allolevalt rongilt kõik kastid õiges järjekorras maha tõsta?
[Täisarv]
Õige vastus on: 7 ringi.
Sawya saeb puutüvedest erineva pikkusega palke. Iga palgi saagimise järel paneb ta selle müügiks välja oma töökoja ette 18 meetri pikkuse tee äärde. Tee on kitsas ja sinna ei mahu kaht palki kõrvuti, sellepärast paneb Sawya palgid alati ühte ritta.
Kui Sawya saeb valmis uue palgi, paneb ta selle tee ääres kõige vasakpoolsemale kohale, kuhu see mahub. Kui ta mõne palgi maha müüb, viib ostja selle ära ilma teisi palke liigutamata.
Mõnede palkide saagimise ja müümise järel näeb tee äär välja selline:
Edasi tahab Sawya lõigata 1m, 2m, 3m ja 4m pikkused palgid. Millises järjekorras ta peaks need lõikama, et need õnnestuks sama süsteemi järgi tee äärde ära paigutada?
[Interaktiivne]
(Lohista palgid õigesse saagimise järjekorda.)
Võimalikud õiged vastused: (4m, 3m, 2m, 1m), (3m, 4m, 2m, 1m), (3m, 2m, 4m, 1m).
Ehituskonstruktori klotsidel on neli tunnust:
laius (klots võib olla kitsas, keskmine või lai);
kõrgus (klots võib olla madal, keskmine või kõrge);
klotsi peal olevate punnide arv (klotsil võib olla null, üks või kaks punni);
klotsi all olevate pesade arv (klotsil võib olla null, üks või kaks pesa).
Kobras tahab oma klotsid jagada kolmest klotsist koosnevatesse gruppidesse vastavalt järgmisele reeglile:
Igas grupis peab igaüks neist neljast tunnusest (iga tunnus eraldi vaadatuna) olema kas kõigil kolmel klotsil sama või kõigil kolmel klotsil erinev.
Näiteks eelnev kolmik on sobiv grupp, sest
kõigi kolme klotsi laiused on samad;
kõigi kolme klotsi kõrgused on erinevad;
kõigi kolme klotsi punnide arvud on erinevad;
kõigi kolme klotsi pesade arvud on erinevad.
Jaga järgmised klotsid reeglile vastavatesse gruppidesse.
[Interaktiivne]
(Lohista klotsid gruppidesse.)
Õige vastus on:
(Loomulikult on õiged ka gruppide omavahelised ümberjärjestused ja klotside omavahelised ümberjärjestused gruppide sees.)
Miale meeldib puhkuse ajal jalgsi matkata ja igal ööl erinevas kohas peatuda. Alloleval joonisel on kujutatud rada, mille ta tahab järgmise puhkuse ajal läbida. Ühe päevaga jõuab Mia läbida kas ühe või kaks joonisel punktiiridega eraldatud rajalõiku.
Joonis näitab plaanitud raja algust () ja lõppu (
) ning võimalikke ööbimiskohti (
).
Joonisel on nooltega näidatud kaks võimalikku raja läbimise plaani. Plaani number 1 järgi läbiks Mia kogu raja kolme ööbimisega, plaani number 2 järgi aga nelja ööbimisega.
Mitu erinevat võimalikku plaani raja läbimiseks Mial kokku on (kaks juba näidatud plaani kaasa arvatud)?
[Täisarv]
Õige vastus on: 6.
Ruairi ja Eabha õpivad tundma vanasti Iirimaal kasutatud ogami kirja. Selles kirjas esitatakse iga täht joonte grupina. Tähti märkivad grupid on üksteisest eraldatud natuke suuremate vahedega.
Eabha kirjutas nelja toiduaine ingliskeelsed nimed ogami kirjas.
Aita Ruairil leida vastavus ogami kirjas ja inglise tähestikus kirjutatud sõnade vahel.
[Interaktiivne]
(Lohista iga inglise tähestikus kirjutatud sõna vastava ogami kirjas sõna all olevasse kasti.)
Õige vastus on:
Robotimängu eesmärk on juhtida oma robot selle lähtekohast tärniga () märgitud ruutu ja ta seal seisma jätta.
Mängus on järgmised reeglid:
Alltoodud näites saab roboti tärniga ruudule kolme käiguga. Esiteks peab robotit
liigutama paremale. See robot liigub kuni takistuseni ja jääb selle ees seisma. Teiseks peab robotit
liigutama üles, kasutades selle peatamiseks takistusena robotit
. Lõpuks peab robotit
liigutama vasakule.
Juhi alloleval mängulaual robot tärniga
ruudule vähima võimaliku käikude arvuga.
[Interaktiivne]
(Roboti valimiseks klõpsa sellel; siis klõpsa robotist selles suunas, kuhu tahad robotit liigutada.)
Õige vastus on: (4 käiguga)
Linnas on suvel väga palav ja linnapea otsustas paigutada mõnedele ristmikele mahlamüügiletid.
Linnapea nõuab, et ükskõik milliselt ristmikult linnas peab olema võimalik jõuda lähima mahlamüügiletini mitte rohkem kui kahe tänava läbimisega.
Linnaplaanil tähistavad punktid ristmikke ja jooned neid ühendavaid tänavaid. Ringid tähistavad ristmikke, kuhu on juba mahlamüügiletid paigutatud.
Leia ristmik, kuhu paigutada veel üks mahlamüügilett, et linnapea nõudmine oleks rahuldatud.
[Interaktiivne]
(Ristmiku valimiseks klõpsa sellel; valiku tühistamiseks klõpsa uuesti.)
Õige vastus on:
Koprakooperatiiv ehitab kopraperedele elamuid. Kooperatiivi töölised on spetsialiseerunud kas vee- või maatöödele.
Ühe suurema elamu ehitus koosneb neljast osast:
| Elamu osa | Ehituse aeg | Veetööd | Maatööd |
|---|---|---|---|
| Terrass | 4 päeva | 3 töölist | 2 töölist |
| Koobas | 3 päeva | 5 töölist | 1 tööline |
| Katus | 5 päeva | 2 töölist | 2 töölist |
| Tamm | 8 päeva | 4 töölist | 2 töölist |
Lisaks ei saa katuse ehitamist alustada enne, kui koobas on valmis.
Koosta tööde tegemiseks plaan, mis võimaldab elamu võimalikult kiiresti valmis saada, kui kasutada on kuni 7 veetööde ja kuni 5 maatööde töölist.
[Interaktiivne]
(Lohista töid kujutavad ristkülikud optimaalseks tööplaaniks.)
Üks võimalik õige vastus on:
Emma on kodus . Tal on vaja teha kolm toimetust ja seejärel koju naasta.
Need kolm toimetust on:
Emma ei tea, kui kaua tal igas kohas läheb, aga ta tahab käimisele kulutada võimalikult vähe aega.
Kaardil on märgitud, mitu minutit tal kulub iga teelõigu läbimiseks. Näiteks kaardil esile tõstetud teekonna korral kulub tal käimisele kokku 4 + 6 + 3 + 9 + 7 + 3 + 6 = 38 minutit.
Kas Emma saaks kõik käigud tehtud ka kiiremini? Võib-olla on kasulik mõnda teelõiku läbida edasi-tagasi (selle peale kulub muidugi kaks korda nii palju aega, kui kaardil selle teelõigu juurde märgitud on)?
Märgi kõige kiirem teekond, mida Emma võiks kasutada. Millistest teelõikudest see koosneb?
[Interaktiivne]
(Teelõigu valimiseks klõpsa sellel; valiku tühistamiseks klõpsa uuesti. Valitud teelõigud on värviga esile tõstetud.)
Õige vastus on:
Bob paigaldas oma korteri uksele koodluku, mille avamiseks tuleb erinevaid numbriklahve õiges järjekorras vajutada.
Alguses valis Bob koodiks

Bob kasutas koodi üleskirjutamiseks süsteemi, kus n >> c tähendab, et koodis on numbrist c vasakul pool täpselt n numbrit, mis on suuremad kui c.
Näiteks kirjutab Bob oma koodi kirjeldusse 1 >> 3, sest koodis on numbrist 3 vasakul pool täpselt 1 numbrist 3 suurem number (see on number 4). Seega on terve viiekohalise koodi kirjeldus Bobi süsteemis
0 >> 0; 3 >> 1; 0 >> 2; 1 >> 3; 0 >> 4.Hiljem otsustas Bob, et viiekohaline kood ei ole piisavalt turvaline. Ta valis uue koodi, mis koosneb numbritest 0 kuni 7 ja mille kirjeldus on
3 >> 0; 2 >> 1; 4 >> 2; 4 >> 3; 1 >> 4; 1 >> 5; 1 >> 6; 0 >> 7.Milline on Bobi uus uksekood?
[Interaktiivne]
(Lohista numbrid tabelisse õigesse järjekorda.)
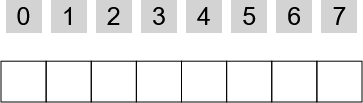
Õige vastus on:

Aritmeetilised avaldised koosnevad järgmistest osadest:
Avaldise struktuuri võib esitada operaatoritest ja operandidest koosneva diagrammina. Sellist diagrammi nimetatakse avaldise süntaksipuuks.
Süntaksipuust saab omakorda koostada avaldise postfiksesituse. Postfiksesituses kirjutatakse kõigepealt operandid ja siis nende järele vastav operaator.
Tabelis on toodud näitena kahe avaldise süntaksipuud ja postfiksesitused.
| Avaldis | Süntaksipuu | Postfiksesitus |
|---|---|---|
| a + b | 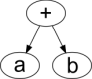 |
a b + |
| (a + 1) · (b + c) | 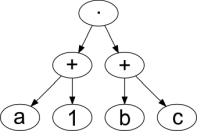 |
a 1 + b c + · |
Milline järgmistest süntaksipuudest vastab avaldisele, mille postfiksesitus on a 1 + b 2 + · 25 c : +?
[Raadionupud]
A. 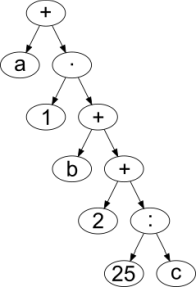 B.
B. 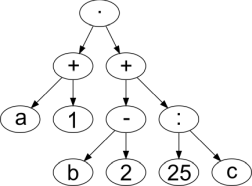 C.
C. 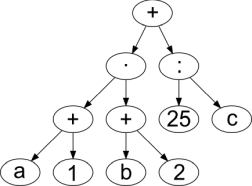 D.
D. 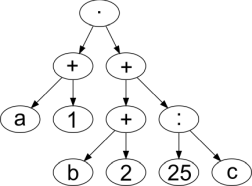
Õige vastus on: C.
Brian on sillaehitaja. Tema uus projekt on ehitada sillad, et tema koduküla  lapsed pääseks uude kooli
lapsed pääseks uude kooli  .
.
Kahjuks ei oska Brian ujuda. See tähendab, et ise üle vee pääsemiseks peab ta kõigepealt silla ehitama. Pärast seda võib üle selle silla käia kuitahes palju kordi.
Sildade ehitamiseks on vaja materjali. Oma kodukülas on Brianil 3 palki. Lisaks võib ta igal ajal liikuda juba sildadega ühendatud saarte vahel ja sealt materjali juurde koguda. Kaart näitab, kui palju palke on vaja erinevate sildade ehitamiseks ja kui palju palke igal saarel saada on.
Iga palki võib silla ehituseks kasutada ainult ühe korra. Mõned palgid võivad ka kasutamata jääda.
Millised sillad peaks Brian ehitama, et luua ühendus koduküla ja kooli vahele vähima võimaliku palkide arvuga?
[Interaktiivne]
(Silla valimiseks klõpsa sellel; valiku tühistamiseks klõpsa uuesti.)
Õige vastus on:
Koprad harjutavad mägimatkaks. Nad matkavad hanereas ja iga kobras kannab kaasas redelit. Kobras, kes jõuab esimesena järsu tõusu juurde, ajab oma redeli püsti ja hoiab seda, et teised koprad saaks üles ronida.
Kõik redeleid hoidvad koprad jäävad paigale ja hoiavad oma redeleid kuni kõik redelit mitte hoidvad koprad on mäe tippu jõudnud. Seejärel ronib iga redelit hoidnud kobras oma redeli abil tippu. Mäe tipus võtavad kõik koprad kohalejõudmise järjekorras ritta. Seejärel laskuvad nad samas järjekorras köiega alla.
Järgnev joonis näitab, kuidas neli kobrast ühe mäe otsa (ja sealt alla) ronivad:
Kuus kobrast lähevad matkale alloleval joonisel näidatud maastikule. Millises järjekorras nad matka lõpetavad?
[Interaktiivne]
(Lohista koprad õiges järjekorras küsimärgi juurde.)
Õige vastus on: 365412.