Денис ищет сокровище, спрятанное под одним из квадратов игрового поля. Он начинает поиск с отмеченного буквой С квадрата, и за один раз он может шагнуть на соседний квадрат, расположенный на той же строчке или в том же столбце. После каждого шага ему сообщают, оказался он чуть ближе («Б») или дальше («Д») от сокровища. Расстояние до сокровища равно наименьшему количеству шагов, необходимых для его обнаружения.
Представим, например, что на поле размером 3x3 сокровище спрятано в квадрате, которое отмечено звёздочкой. Денис начинает поиск с отмеченного буквой С квадрата и делает два шага вниз. Тогда расстояние от сокровища до каждого квадрата, где находится мальчик, будет таким, как показано на нижеприведённом рисунке справа. Таким образом, после первого шага Денис получил сигнал «Б», а после второго — сигнал «Д», как показано на нижеприведённом рисунке слева:
Теперь Денис играет на поле размером 4x7. Его шаги и полученные сигналы представлены на нижеприведённом рисунке. В каком квадрате спрятано сокровище?
[Интерактивное]
(Щёлкни на квадрат, чтобы его выбрать; щёлкни на него ещё раз, чтобы отменить свой выбор.)
Правильный ответ:
.
Том живёт в деревне, где всего шесть домов (считая и его дом). Особенность деревни в том, что все тропинки в этой деревне имеют одинаковую длину.
Том составил карту, на которой отметил только самые короткие пути от своего дома до всех других домов в деревне. На этой карте не обязательно отмечены все существующие в деревне тропинки, потому что Том отметил на карте только самые короткие пути от своего дома до других домов.
Мы не знаем, как выглядела бы карта деревни, если бы на ней были отмечены все тропинки. Но какой из перечисленных карт она точно не может быть?
[Raadionupud]
A. B.
C.
D.
Правильный ответ: C.
В каждом вагоне товарного поезда имеется по одному ящику. Для их снятия с вагона используется один кран, который стоит на месте и не двигается. Ящик должен находиться точно под краном, чтобы его можно было снять с вагона.
Ящики пронумерованы, и их нужно снимать с вагонов по порядку, начиная с ящика номер 1. Поезд может двигаться только вперёд, но он двигается по кольцевой дороге. При необходимости поезд может отъехать от крана, сделать круг и вернуться обратно под кран.
В приведённом выше примере ящики необходимо снять по порядку, то есть 1, 2, 3, 4. На первом круге кран должен пропустить ящик 4, снять ящик 1, далее пропустить ящик 3 и снять ещё ящик 2. На втором круге кран должен пропустить ящик 4, но снять ящик 3. На третьем круге кран сможет, наконец-то, снять ящик 4.
Сколько кругов должен проехать нижеприведённый поезд, чтобы кран смог снять все имеющиеся на нём ящики по порядку?
[Täisarv]
Правильный ответ: 7 кругов.
Сергей распиливает стволы деревьев на брёвна разной длины. После каждого распила Сергей выставляет брёвна на продажу, выкладывая их вдоль 18-метровой обочины дороги перед своей мастерской. Дорога узкая, и два бревна не помещаются рядом, поэтому Сергей всегда выкладывает брёвна в один ряд.
Когда у Сергея появляется новое отпиленное бревно, он кладёт его на самый левый край дороги, куда это бревно может поместиться. Когда бревно продано, то покупатель забирает его, но оставшиеся брёвна не передвигаются.
После распиливания некоторых стволов и продажи некоторых брёвен обочина дороги выглядит следующим образом:
Далее Сергей хочет получить брёвна, длина которых была бы 1м, 2м, 3м и 4м. В каком порядке он должен их отпилить, чтобы брёвна можно было разместить на дороге по той же системе?
[Interaktiivne]
(Перетащи брёвна в порядке их получения.)
Возможные правильные ответы: (4м, 3м, 2м, 1м), (3м, 4м, 2м, 1м), (3м, 2м, 4м, 1м).
Детали строительного конструктора обладают четырьмя свойствами:
ширина (деталь может быть узкой, средней или широкой);
высота (деталь может быть низкой, средней или высокой);
количество выпуклостей на детали (на детали может быть ноль, одна или две выпуклости);
количество гнёзд внизу детали (у детали может быть ноль, одно или два гнезда).
Бобр хочет разделить свои детали на группы (в каждой группе по три детали), соблюдая следующее правило:
В каждой группе каждое из этих четырёх свойств (каждое свойство рассматривается отдельно) должно быть либо одинаковым для всех трёх деталей, либо разным для всех трёх деталей.
Например, приведённая выше группа из трёх деталей соответствует правилу, потому что
у всех трёх деталей одинаковая ширина;
у всех трёх деталей разная высота;
у всех трёх деталей разное количество выпуклостей;
у всех трёх деталей разное количество гнёзд.
Раздели следующие детали на группы, соблюдая правила.
[Interaktiivne]
(Перетащи детали в группы.)
Правильный ответ:
(Конечно, взаимное переупорядочение групп и взаимное переупорядочение деталей внутри групп тоже правильно.)
Во время каникул Маше нравится ходить в походы пешком и каждую ночь останавливаться на ночлег в разных местах. На нижеприведённом рисунке показан маршрут, который она хочет пройти во время следующих каникул. За один день Маша может пройти один или два участка, отмеченных на рисунке пунктирами.
На рисунке изображено начало () и конец (
) запланированного маршрута, а также возможные места ночёвок (
).
Стрелками на рисунке изображены два возможных плана прохождения маршрута. Если следовать плану номер 1, то во время прохождения маршрута Маша остановиться на три ночлега; план номер 2 потребует четыре остановки на ночлег.
Сколько всего различных возможных планов прохождения этого маршрута (включая два уже показанных) есть у Маши?
[Täisarv]
Правильный ответ: 6.
Маргарита и Эрвин изучают распространённое в древности в Ирландии огамическое письмо. В этом письме каждая буква представлена в виде группы линий. Группы, обозначающие буквы, отделены друг от друга чуть большими промежутками.
Используя огамическое письмо, Эрвин записал английские названия четырёх продуктов питания.
Помоги Маргарите найти соответствие между словами, записанными с помощью огамического письма и английского алфавита.
[Интерактивное]
(Перетащи каждое слово, записанное с помощью английского алфавита, в ячейку, которая соответствует слову, записанному с помощью огамического письма.)
Правильный ответ:
Цель игры — сделать так, чтобы робот игрока переместился c первоначального квадрата на квадрат, который отмечен звёздочкой ().
В игре есть несколько правил:
На нижеприведённом примере показано как робот сможет переместиться на отмеченный звёздочкой квадрат за три шага. Для этого робот
сначала переместится направо (он будет двигаться до препятствия и остановится перед ним). Далее робот
переместится наверх, и использует робота
как препятствие. И наконец робот
переместится налево.
На нижеприведённом поле направь робота в квадрат со звёздочкой
, используя наименьшее возможное число шагов.
[Interaktiivne]
(Щёлкни на робота, чтобы его выбрать; далее щёлкни в том направлении, куда следует переместить робота.)
Правильный ответ: (за 4 шага)
Летом в городе очень жарко, и на некоторых перекрёстках мэр решил установить киоски по продаже соков.
Мэр потребовал, чтобы от любого перекрёстка до ближайшего киоска можно было бы добраться, пройдя не более двух улиц.
На плане города точки обозначают перекрёстки, а линии — это соединяющие их улицы. Кружочки обозначают перекрёстки, где уже установлены киоски по продаже соков.
Найди перекрёсток, где должен располагаться ещё один киоск по продаже соков, чтобы требование мэра было выполнено.
[Интерактивное]
(Щёлкни на перекрёсток, чтобы его выбрать; щёлкни на него ещё раз, чтобы отменить свой выбор.)
Правильный ответ:
Кооператив "Бобрики" строит дома для бобровых семей. Рабочие кооператива выполняют водные или земляные работы.
Строительство одного большого дома состоит из четырёх частей:
| Часть дома | Время строительства | Водные работы | Земляные работы |
|---|---|---|---|
| Терраса | 4 дня | 3 рабочих | 2 рабочих |
| Пещера | 3 дня | 5 рабочих | 1 рабочий |
| Крыша | 5 дней | 2 рабочих | 2 рабочих |
| Плотина | 8 дней | 4 рабочих | 2 рабочих |
Известно, что строительство крыши нельзя начать до тех пор, пока не будет построена пещера.
Составь план выполнения работ, позволяющий построить дом как можно быстрее, если в строительстве дома будет задействовано до 7 рабочих по водным работам и до 5 рабочих по земляным работам.
[Interaktiivne]
(Перетащи обозначающие работы прямоугольники так, чтобы получился оптимальный план выполнения работ.)
Один из возможных правильных ответов:
Сейчас Эмма находится дома . Девочка должна выполнить три поручения и вернуться домой.
Она должна:
Эмма не знает, сколько времени она проведёт в каждом из этих мест, но она хочет потратить на прохождение пути наименьшее возможное количество времени.
На карте отмечено, сколько минут ей потребуется для прохождения каждого участка пути. Например, в случае отмеченного на карте пути ей понадобится всего 4 + 6 + 3 + 9 + 7 + 3 + 6 = 38 минут, чтобы его пройти.
Смогла бы Эмма выполнить все перемещения быстрее? Возможно, было бы полезнее пройти некоторые участки пути туда и обратно (что, конечно, займёт в два раза больше времени, чем указано на карте для данного участка)?
Отметь самый быстрый путь, которым может воспользоваться Эмма. Из каких участков он состоит?
[Interaktiivne]
(Щёлкни на участок пути, чтобы его выбрать; щёлкни на него ещё раз, чтобы отменить свой выбор. Выбранные участки отмечены другим цветом.)
Правильный ответ:
Боб установил на дверь своей квартиры кодовый замок, который можно открыть, нажав в правильной последовательности различные кнопки с цифрами.
Сначала Боб выбрал код

Для записи кода Боб использовал систему, в которой n >> c обозначает, что слева от цифры c в коде находится ровно n цифр, которые больше c.
Например, Боб записал часть своего кода как 1 >> 3, потому что слева от цифры 3 в коде находится ровно 1 цифра, которая больше 3 (это цифра 4). Таким образом, запись всего пятизначного кода в системе Боба выглядит так
0 >> 0; 3 >> 1; 0 >> 2; 1 >> 3; 0 >> 4.Позже Боб решил, что пятизначный код не является достаточно безопасным. Он выбрал новый код, который состоит из цифр от 0 до 7, и в системе Боба выглядит так
3 >> 0; 2 >> 1; 4 >> 2; 4 >> 3; 1 >> 4; 1 >> 5; 1 >> 6; 0 >> 7.Какой новый код для двери придумал Боб?
[Interaktiivne]
(Перетащи цифры в правильные ячейки таблицы.)
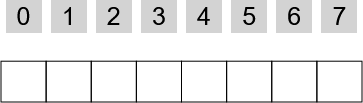
Правильный ответ:

Арифметические выражения состоят из следующих частей:
Структуру выражения можно представить как диаграмму, которая состоит из операторов и операндов. Такую диаграмму называют синтаксическим деревом выражения.
В свою очередь из синтаксического дерева можно составить постфиксную форму выражения. В постфиксной форме сначала записываются операнды, за которыми следует соответствующий оператор.
В таблице приведены примеры синтаксических деревьев и постфиксных форм двух выражений.
| Выражение | Синтаксическое дерево | Постфиксная форма |
|---|---|---|
| a + b | 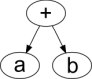 |
a b + |
| (a + 1) · (b + c) | 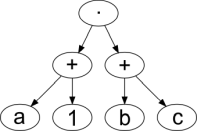 |
a 1 + b c + · |
Какое из нижеприведённых синтаксических деревьев соответствует выражению, постфиксная форма которого a 1 + b 2 + · 25 c : +?
[Raadionupud]
A. 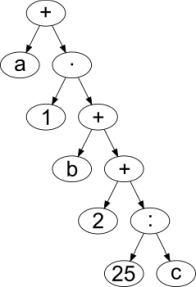 B.
B. 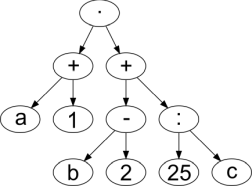 C.
C. 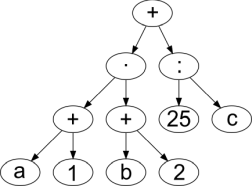 D.
D. 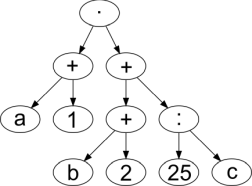
Правильный ответ: C.
Марк работает строителем мостов. Сейчас он разрабатывает проект строительства мостов, благодаря которому дети из его родной деревни  смогут ходить в новую школу
смогут ходить в новую школу  .
.
К сожалению, Марк не умеет плавать. Поэтому он должен сначала построить мост, чтобы самому перебраться через воду. После этого по этому мосту можно ходить любое количество раз.
Для строительства мостов нужны материалы. В родной деревне у Марка есть 3 бревна. Кроме того, в любой момент он может пойти на острова, уже соединённые мостами, и взять там строительный материал. На карте показано, сколько брёвен необходимо для постройки различных мостов, и сколько брёвен можно найти на каждом острове.
Каждое бревно можно использовать для постройки моста только один раз. Некоторые брёвна могут остаться и неиспользованными.
Какие мосты должен построить Марк, используя наименьшее количество брёвен, чтобы соединить родную деревню со школой?
[Interaktiivne]
(Щёлкни на мост, чтобы его выбрать; щёлкни на него ещё раз, чтобы отменить свой выбор.)
Правильный ответ
Бобры готовятся к походу в горы. Они идут друг за другом, и каждый бобр несёт лестницу. Бобр, который добирается до крутого подъема первым, поднимает свою лестницу и держит её, чтобы остальные бобры смогли подняться.
Все бобры, держащие лестницы, остаются на месте и держат свои лестницы до тех пор, пока все не держащие лестницы бобры не достигнут вершины горы. Затем каждый бобр, держащий лестницу, поднимается на вершину по своей лестнице. На вершине все бобры займут свои места в том порядке, в котором они добрались до вершины. Затем они спускаются по веревке вниз в том же порядке.
Следующий рисунок показывает, как четыре бобра забирались на вершину горы (и оттуда спускались):
Шесть бобров отправились в поход по местности, которая показана на нижеприведённом рисунке. В каком порядке они завершат поход?
[Interaktiivne]
(Перетащи бобров к знаку вопроса в правильном порядке.)
Правильный ответ: 365412.