Miale meeldib puhkuse ajal jalgsi matkata ja igal ööl erinevas kohas peatuda. Alloleval joonisel on kujutatud rada, mille ta tahab järgmise puhkuse ajal läbida. Ühe päevaga jõuab Mia läbida kas ühe või kaks joonisel punktiiridega eraldatud rajalõiku.
Joonis näitab plaanitud raja algust () ja lõppu (
) ning võimalikke ööbimiskohti (
).
Joonisel on nooltega näidatud kaks võimalikku raja läbimise plaani. Plaani number 1 järgi läbiks Mia kogu raja kolme ööbimisega, plaani number 2 järgi aga nelja ööbimisega.
Mitu erinevat võimalikku plaani raja läbimiseks Mial kokku on (kaks juba näidatud plaani kaasa arvatud)?
[Täisarv]
Õige vastus on: 6.
Ruairi ja Eabha õpivad tundma vanasti Iirimaal kasutatud ogami kirja. Selles kirjas esitatakse iga täht joonte grupina. Tähti märkivad grupid on üksteisest eraldatud natuke suuremate vahedega.
Eabha kirjutas nelja toiduaine ingliskeelsed nimed ogami kirjas.
Aita Ruairil leida vastavus ogami kirjas ja inglise tähestikus kirjutatud sõnade vahel.
[Interaktiivne]
(Lohista iga inglise tähestikus kirjutatud sõna vastava ogami kirjas sõna all olevasse kasti.)
Õige vastus on:
Robotimängu eesmärk on juhtida oma robot selle lähtekohast tärniga () märgitud ruutu ja ta seal seisma jätta.
Mängus on järgmised reeglid:
Alltoodud näites saab roboti tärniga ruudule kolme käiguga. Esiteks peab robotit
liigutama paremale. See robot liigub kuni takistuseni ja jääb selle ees seisma. Teiseks peab robotit
liigutama üles, kasutades selle peatamiseks takistusena robotit
. Lõpuks peab robotit
liigutama vasakule.
Juhi alloleval mängulaual robot tärniga
ruudule vähima võimaliku käikude arvuga.
[Interaktiivne]
(Roboti valimiseks klõpsa sellel; siis klõpsa robotist selles suunas, kuhu tahad robotit liigutada.)
Õige vastus on: (4 käiguga)
Keeltekool plaanib suvel korraldada neli kursust. Allolev joonis näitab, milliseid keeli iga õpetaja õpetada oskab.
Igale kursusele tuleb määrata õpetaja ja igale õpetajale saab määrata ainult ühe kursuse. Õpetajad, kellele kursust ei määrata, saavad endale muu töö.
Milline järgmistest väidetest on kindlasti õige?
[Raadionupud]
A. Neli õpetajat jäävad kursuseta ja saavad muu töö.
B. Õpetaja D õpetab hispaania keele kursust  .
.
C. Õpetaja E õpetab itaalia keele kursust  .
.
D. Kui õpetajad B, F ja G pole saadaval, tuleb üks kursus ära jätta.
Õige vastus on: D (kui õpetajad B, F ja G pole saadaval, tuleb üks kursus ära jätta).
Koprakooperatiiv ehitab kopraperedele elamuid. Kooperatiivi töölised on spetsialiseerunud kas vee- või maatöödele.
Ühe suurema elamu ehitus koosneb neljast osast:
| Elamu osa | Ehituse aeg | Veetööd | Maatööd |
|---|---|---|---|
| Terrass | 4 päeva | 3 töölist | 2 töölist |
| Koobas | 3 päeva | 5 töölist | 1 tööline |
| Katus | 5 päeva | 2 töölist | 2 töölist |
| Tamm | 8 päeva | 4 töölist | 2 töölist |
Lisaks ei saa katuse ehitamist alustada enne, kui koobas on valmis.
Koosta tööde tegemiseks plaan, mis võimaldab elamu võimalikult kiiresti valmis saada, kui kasutada on kuni 7 veetööde ja kuni 5 maatööde töölist.
[Interaktiivne]
(Lohista töid kujutavad ristkülikud optimaalseks tööplaaniks.)
Üks võimalik õige vastus on:
Emma on kodus . Tal on vaja teha kolm toimetust ja seejärel koju naasta.
Need kolm toimetust on:
Emma ei tea, kui kaua tal igas kohas läheb, aga ta tahab käimisele kulutada võimalikult vähe aega.
Kaardil on märgitud, mitu minutit tal kulub iga teelõigu läbimiseks. Näiteks kaardil esile tõstetud teekonna korral kulub tal käimisele kokku 4 + 6 + 3 + 9 + 7 + 3 + 6 = 38 minutit.
Kas Emma saaks kõik käigud tehtud ka kiiremini? Võib-olla on kasulik mõnda teelõiku läbida edasi-tagasi (selle peale kulub muidugi kaks korda nii palju aega, kui kaardil selle teelõigu juurde märgitud on)?
Märgi kõige kiirem teekond, mida Emma võiks kasutada. Millistest teelõikudest see koosneb?
[Interaktiivne]
(Teelõigu valimiseks klõpsa sellel; valiku tühistamiseks klõpsa uuesti. Valitud teelõigud on värviga esile tõstetud.)
Õige vastus on:
Bob paigaldas oma korteri uksele koodluku, mille avamiseks tuleb erinevaid numbriklahve õiges järjekorras vajutada.
Alguses valis Bob koodiks

Bob kasutas koodi üleskirjutamiseks süsteemi, kus n >> c tähendab, et koodis on numbrist c vasakul pool täpselt n numbrit, mis on suuremad kui c.
Näiteks kirjutab Bob oma koodi kirjeldusse 1 >> 3, sest koodis on numbrist 3 vasakul pool täpselt 1 numbrist 3 suurem number (see on number 4). Seega on terve viiekohalise koodi kirjeldus Bobi süsteemis
0 >> 0; 3 >> 1; 0 >> 2; 1 >> 3; 0 >> 4.Hiljem otsustas Bob, et viiekohaline kood ei ole piisavalt turvaline. Ta valis uue koodi, mis koosneb numbritest 0 kuni 7 ja mille kirjeldus on
3 >> 0; 2 >> 1; 4 >> 2; 4 >> 3; 1 >> 4; 1 >> 5; 1 >> 6; 0 >> 7.Milline on Bobi uus uksekood?
[Interaktiivne]
(Lohista numbrid tabelisse õigesse järjekorda.)
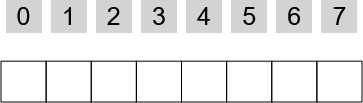
Õige vastus on:

Aritmeetilised avaldised koosnevad järgmistest osadest:
Avaldise struktuuri võib esitada operaatoritest ja operandidest koosneva diagrammina. Sellist diagrammi nimetatakse avaldise süntaksipuuks.
Süntaksipuust saab omakorda koostada avaldise postfiksesituse. Postfiksesituses kirjutatakse kõigepealt operandid ja siis nende järele vastav operaator.
Tabelis on toodud näitena kahe avaldise süntaksipuud ja postfiksesitused.
| Avaldis | Süntaksipuu | Postfiksesitus |
|---|---|---|
| a + b | 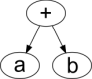 |
a b + |
| (a + 1) · (b + c) | 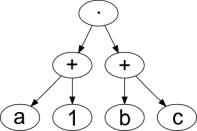 |
a 1 + b c + · |
Milline järgmistest süntaksipuudest vastab avaldisele, mille postfiksesitus on a 1 + b 2 + · 25 c : +?
[Raadionupud]
A. 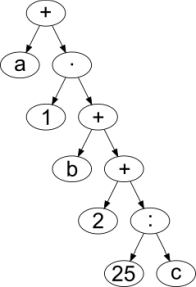 B.
B. 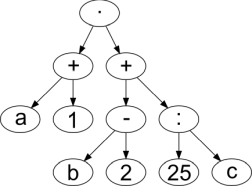 C.
C. 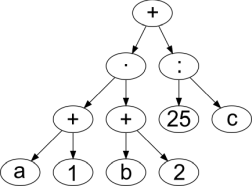 D.
D. 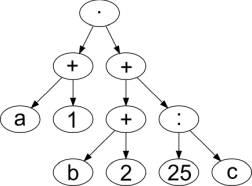
Õige vastus on: C.
Brian on sillaehitaja. Tema uus projekt on ehitada sillad, et tema koduküla  lapsed pääseks uude kooli
lapsed pääseks uude kooli  .
.
Kahjuks ei oska Brian ujuda. See tähendab, et ise üle vee pääsemiseks peab ta kõigepealt silla ehitama. Pärast seda võib üle selle silla käia kuitahes palju kordi.
Sildade ehitamiseks on vaja materjali. Oma kodukülas on Brianil 3 palki. Lisaks võib ta igal ajal liikuda juba sildadega ühendatud saarte vahel ja sealt materjali juurde koguda. Kaart näitab, kui palju palke on vaja erinevate sildade ehitamiseks ja kui palju palke igal saarel saada on.
Iga palki võib silla ehituseks kasutada ainult ühe korra. Mõned palgid võivad ka kasutamata jääda.
Millised sillad peaks Brian ehitama, et luua ühendus koduküla ja kooli vahele vähima võimaliku palkide arvuga?
[Interaktiivne]
(Silla valimiseks klõpsa sellel; valiku tühistamiseks klõpsa uuesti.)
Õige vastus on:
Koprad harjutavad mägimatkaks. Nad matkavad hanereas ja iga kobras kannab kaasas redelit. Kobras, kes jõuab esimesena järsu tõusu juurde, ajab oma redeli püsti ja hoiab seda, et teised koprad saaks üles ronida.
Kõik redeleid hoidvad koprad jäävad paigale ja hoiavad oma redeleid kuni kõik redelit mitte hoidvad koprad on mäe tippu jõudnud. Seejärel ronib iga redelit hoidnud kobras oma redeli abil tippu. Mäe tipus võtavad kõik koprad kohalejõudmise järjekorras ritta. Seejärel laskuvad nad samas järjekorras köiega alla.
Järgnev joonis näitab, kuidas neli kobrast ühe mäe otsa (ja sealt alla) ronivad:
Kuus kobrast lähevad matkale alloleval joonisel näidatud maastikule. Millises järjekorras nad matka lõpetavad?
[Interaktiivne]
(Lohista koprad õiges järjekorras küsimärgi juurde.)
Õige vastus on: 365412.
Anna ja Ben tahavad teada, kui nad üksteisega nõus ei ole, aga nad ei taha tülitseda. Sellepärast otsustasid nad ehitada eriarvamuste detektori: seadme, mis süütab märgutule, kui neil on mõnes JAH/EI vastusega küsimuses erinevad arvamused.
Nad kasutavad detektori ehitamiseks elemente, mis võivad olla kahes olekus, kas JAH või EI. Kaks elementi võivad olla omavahel ühendatud juhtmega, mis edastab kas positiivse (+) või negatiivse (−) signaali. Element, mis on olekus JAH, edastab signaali kõigisse temast väljuvatesse juhtmetesse. Järgmised elemendid lähevad olekusse JAH, kui nad saavad positiivseid signaale rohkem kui negatiivseid; vastasel juhul (ka siis, kui nad ei saa üldse mingeid signaale), lähevad nad olekusse EI.
Iga sellistest elementidest koosnev seade sisaldab kahte sisendelementi A ja B (üks Anna, teine Beni jaoks) ja ühte väljundelementi Z. Märgutuli süttib, kui väljundelement Z on olekus JAH.
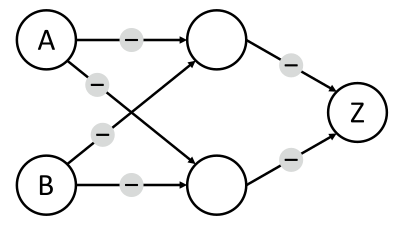
Alguses ehitasid Anna ja Ben alloleval joonisel kujutatud seadme. Selle element Z läheb olekusse JAH siis ja ainult siis, kui element A on olekus JAH ja element B olekus EI.
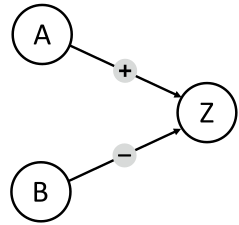
Järgmiseks ehitasid Anna ja Ben alloleval joonisel kujutatud seadme. Selle element Z peab minema olekusse JAH, kui elemendid A ja B on erinevates olekutes (kas A olekus JAH ja B olekus EI, või, vastupidi, A olekus EI ja B olekus JAH). Vastasel juhul (kui elemendid A ja B on samas olekus), peab element Z minema olekusse EI.
Kahjuks pole uue seadme juhtmed praegu veel õigesti häälestatud. Määra iga juhe edastama kas positiivset või negatiivset signaali, et detektor õigesti töötaks!
[Interaktiivne]
(Signaali liigi muutmiseks klõpsa juhtmel oleval märgil.)
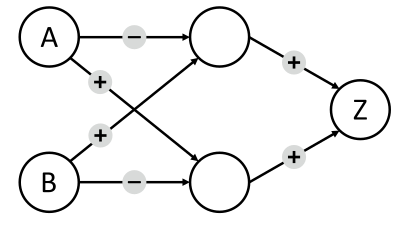
Võimalikud õiged vastused: 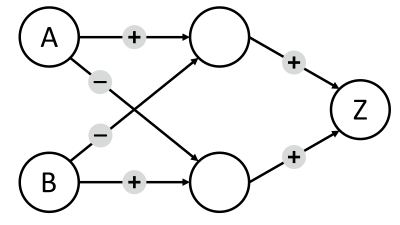 ,
, 
Bruno läks poodi endale uusi kingi ostma. Kingad on riiulile paigutatud, nagu näha joonisel: alumistel riiulitel lühemad ja ülemistel pikemad ning vasakul kitsamad ja paremal laiemad.
Bruno ei tea oma jalgade pikkust ega laiust ja peab õige suurusega kingade leidmiseks neid jalga proovima. Õige suurusega kingadel on õige nii pikkus kui ka laius.
Brunol on kaval meetod, mis garanteerib, et ta ei pea õige suuruse leidmiseks proovima rohkem kui kolme kinga.
Millises järjekorras Bruno kingi proovib?
[Interaktiivne]
(Klõpsa kingadel nende proovimise järjekorras, kuni leiad õige suuruse. Et kontrollida, kas sinu strateegia töötab, kui sa vastust ette ei tea, valitakse ülesande taaskäivitamisel uus Bruno jala suurus ja eelmise katse vastus enam ei kehti.)

Õige vastus on: alustada tuleb keskmisest kingast; teisena tuleb proovida keskmist selles 3×3 ruudus, mis jääb keskmisest kingast õiges suunas; kolmandana tuleb proovida seda, mis on teisena proovitu naaber õiges suunas.
Bruno ja Ernst aitavad informaatikamuuseumis remonti teha. Neile anti ülesandeks ühe 16x16-meetrise näitusesaali põrandale muster värvida.
Mustri kirjeldus on antud mitmel lehel. Igal lehel on number ja lehed võivad numbritega üksteisele viidata. Lisaks on igal lehel ka mõõtkava.
Näiteks sellise kolmel lehel antud kirjelduse järgi peaks värvima 10x10-meetrise koprapildi:
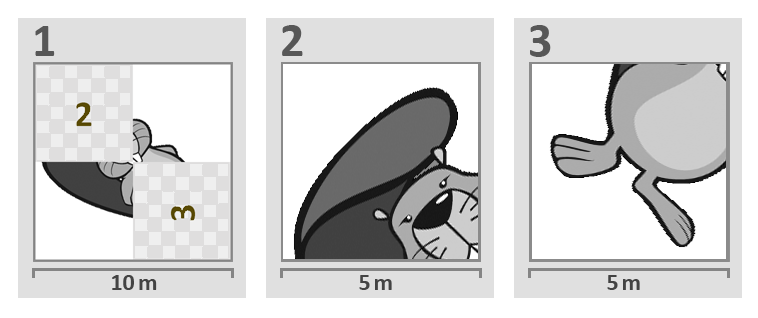
Bruno ja Ernst said sellise kirjelduse:
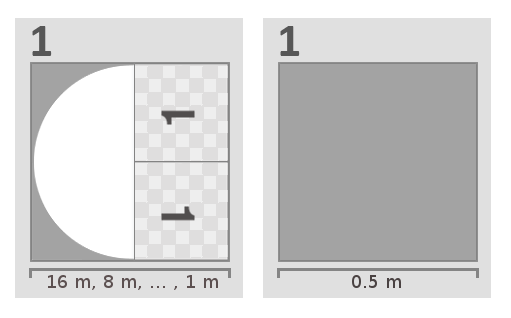
Üks leht viitab iseendale ja mõlemal lehel on sama number! Ernst ei mõista, kuidas selline asi võimalik on. Bruno vastab talle: "Nii saab teha küll. Teine leht ütleb meile, millal lõpetada."
Millise mustri sõbrad saali põrandale värvima peaks?
[Raadionupud]
A.  B.
B.  C.
C.  D.
D. 
Õige vastus on: B.
Teksti esitamisel prefikskoodina määratakse igale tähele ühest või mitmest numbrist koosnev kood nii, et ühegi tähe kood ei ole ühegi teise tähe koodi algus.
Näiteks, kui tähe A koodiks määrata 12, siis võib B koodiks määrata 2 (sest 2 ei ole 12 algus ja ka vastupidi). Seejärel võib C koodiks määrata 11 (sest 11 ei ole ei 2 ega 12 algus ja ka vastupidi), aga mitte 21 (sest B kood 2 oleks 21 algus) ega ka 121 (sest A kood 12 oleks 121 algus).
Tükelda järgnev numbrijada nii, et saadud osad oleks sõna BEBRAS tähtede koodid mingis prefikskoodis.
[Interaktiivne]
(Eraldaja lisamiseks klõpsa kahe numbri vahekohas; eemaldamiseks klõpsa uuesti.)
12112233321
Õige vastus on: 1|21|1|22|33|321.
Doominokivid koosnevad kahest poolest. Iga kivi kummalgi poolel on 1 kuni 6 täppi.
Selles ülesandes on vaja panna antud kaheksa kivi ritta nii, et
kõik kaheksa kivi on kasutatud;
järjestikuste kivide üksteist puutuvatel pooltel on sama arv täppe:
Korrektses reas on kõik kaheksa kivi mingis kindlas järjekorras. Üldiselt näeb iga korrektne rida välja selline:
Korrektse rea saamiseks võib kive võtta mitmes erinevas järjekorras, aga on mõned kivid, mis pole üheski korrektses reas otsmised.
Millised kivid võivad otsmised olla?
(Märgi kõik õiged variandid.)
[Interaktiivne]
(Kivi märkimiseks klõpsa sellel; märke eemaldamiseks klõpsa uuesti.)
Õige vastus on: