

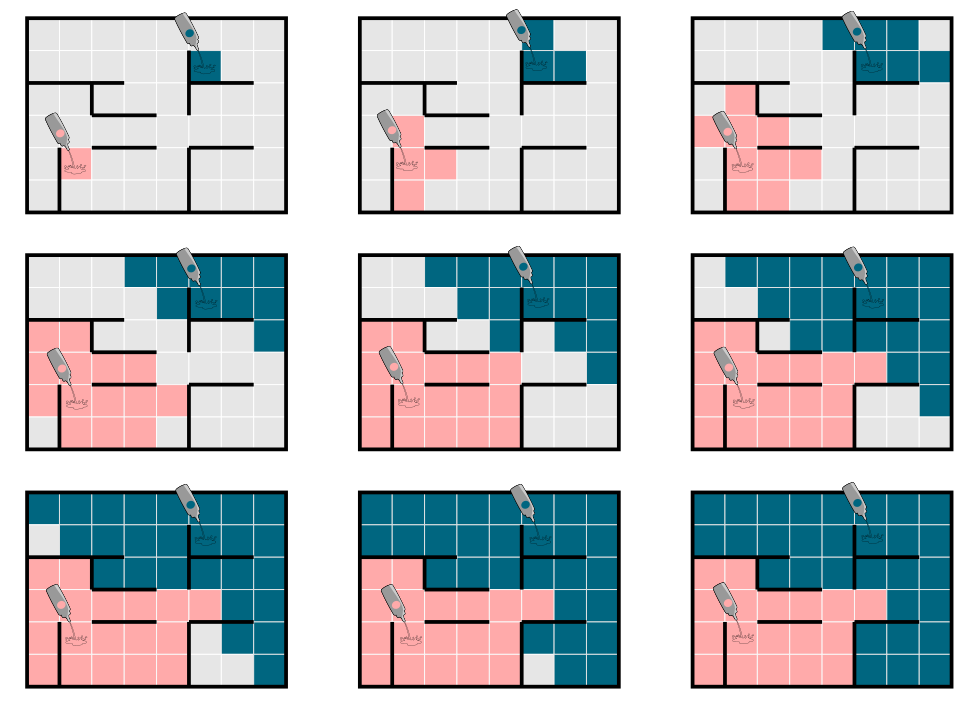
Kui koprad valavad värvi labürindi põrandale, voolab see igal sekundil juba värvitud ruutude naaberruutudesse. Nagu näha alloleval joonisel, voolab värv ainult mööda põrandat, aga mitte läbi seinte.
| Algus | 1. sekund | 2. sekund | 3. sekund |
|---|---|---|---|
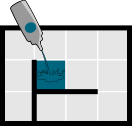 |
 |
 |
 |
Kui koprad valavad põrandale korraga mitut värvi, täidab iga ruudu see värv, mis jõuab sinna esimesena. Kui mõne ruudu juurde jõuavad mitu värvi korraga, täidab selle ruudu kõige tumedam värv.
| Algus | 1. sekund | 2. sekund |
|---|---|---|
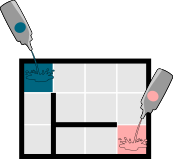 |
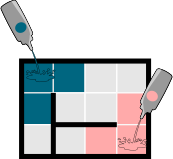 |
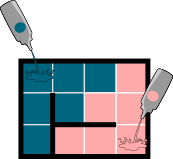 |
Koprad valasid allpool näidatud labürindi põrandale kaht värvi.
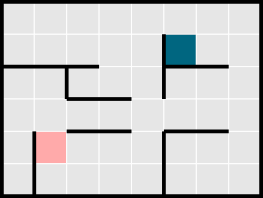
Milline on tulemus?
[Raadionupud]
A. 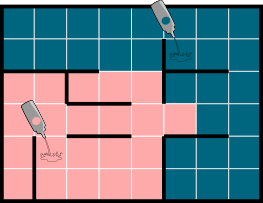 B.
B. 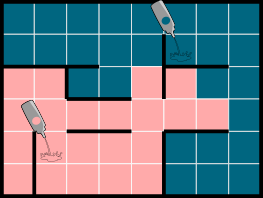 C.
C. 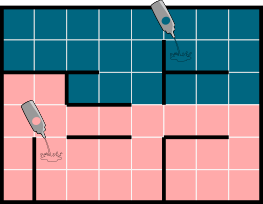 D.
D. 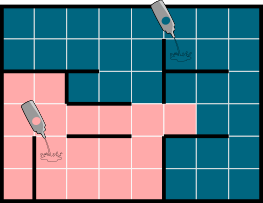
Õige vastus on: D.
Allolev joonis näitab värvide voolamist sekundite kaupa.

Klaaral on printer, mis trükib valgetele laualinadele ruutudest ja ringidest koosnevaid mustreid.
Klaara programmeeris printeri töötama järgmiste reeglite järgi:
Milline järgnevatest mustritest ei saa olla trükitud selle programmi järgi?
[Raadionupud]
A.  B.
B.  C.
C.  D.
D. 
Õige vastus on: C.
C. 
Klaara programm ei saa seda mustrit trükkida, sest selles mustris on iga ringi peal vähemalt üks ruut. Klaara programmi järgi trükitakse kujundeid järjekorras ruut, ring, ruut, ring, ruut, ring. See tähendab, et viimasena trükitud ringi peal ruutu olla ei saa.
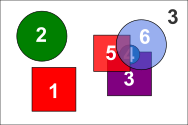
A. 
Selle mustri võib Klaara programm trükkida nii: suurem punane ruut, sinine ring, sinine ruut, üks kollastest ringidest (ükskõik kumb), väiksem punane ruut, teine kollane ring.
B. 
Ka selle mustri võib Klaara programm trükkida. Lõpptulemuses on näha ainult kaks ringi. See tähendab, et üks ring trükiti sellise suurusega ja sellisesse kohta, et see jäi üleni hiljem trükitud kujundite alla. Üks võimalik trükkimiste järjekord on näidatud alloleval joonisel.
D. 
Selle mustri võib Klaara programm trükkida nii: lilla ruut, väiksem lilla ring, kollane ruut, suurem lilla ring, sinine ruut, roheline ring.

Jessica uurib vana muusikaraamatut. Selles on skeem, kus iga noodi juurest algavad nooled näitavad, millised teised noodid võivad meloodias sellele järgneda. Seejuures võib iga noot meloodias esineda ükskõik kui palju kordi.
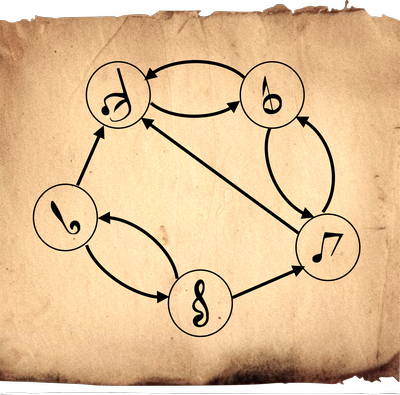
Raamatus on ka järgneva meloodia noodid. Kahjuks on just selles lehes auk.

Millised noodid võisid augu kohas olla?
[Raadionupud]
A. 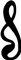
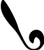
B. 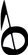
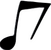
C. 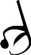
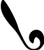
D. 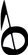
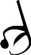
Õige vastus on: B.
Järgnevas on iga vale vastuse juures punasega maha tõmmatud see noot, mis ei või reeglite kohaselt talle eelnevale noodile järgneda.
A. 
B. 
C. 
D. 

Digikell kasutab numbrite näitamiseks LED-indikaatoreid. Igal indikaatoril on seitse segmenti, mida saab lülitada sisse ja välja. Alloleval joonisel on näha, kuidas selliste indikaatoritega näidatakse numbreid 0 ja 2.

Kopra toa seinal oleval kellal on kõige parempoolsem indikaator natuke rikkis: selle seitsmest segmendist üks ei lülitu sisse.
Alloleval joonisel on selle kella näidud viimase kolme minuti jooksul.

Mida näitab kell järgmisel minutil?
[Raadionupud]
A.  B.
B.  C.
C.  D.
D. 
Õige vastus on: B.
Ülesande tekstis olevalt jooniselt on näha, et kolme minuti jooksul näitas kell parempoolse numbri väärtusi (1, 2, 3) õigesti. See tähendab, et alloleval joonisel vasakul punasega näidatud segmendid lülitusid sisse. Seega peab rikkis olema alloleval joonisel paremal punasega näidatud segment.


Järgmisel minutil on kell 01:14. Kui indikaator oleks korras, siis peaks parempoolseim number (4) olema selline, nagu näha alloleval joonisel vasakul. Kuna aga selle indikaatori üks segment on rikkis, siis on tulemus, nagu näha alloleval joonisel paremal.


Seega ongi kella näit järgmisel minutil selline, nagu kujutatud vastusevariandis B.

Mänguasjatehases on kolm masinat. Iga masin teeb kindlat operatsiooni. Mänguasjad läbivad masinaid alati samas järjekorras.
Esimene masin valmistab mänguasju. Iga selle masina käsk koosneb ühest tähest ja ühest numbrist:
| Täht = kuju | Number = värv/muster |
|---|---|
| A = kobras | 1 = sinised triibud |
| B = vedur | 2 = punased täpid |
| C = jojo | 3 = roheline |
Näiteks käsu [A,2] peale valmistab masin punasetäpilise kopra:

Teine masin paneb mõned esimese masina valmistatud mänguasjad kõrvale, sest uuringud on näidanud, et need lastele ei meeldi. Kõrvale pannakse kolme liiki mänguasjad:



Kolmas masin pakib mänguasjad karpidesse. Iga karbi maht on 8 ühikut. Jojo võtab karbis ruumi 1 ühiku, vedur 2 ühikut ja kobras 3 ühikut.
Milline järgmistest käsujadadest annab tulemuseks ühe täpselt täis karbi?
(Mänguasjad peavad ühte karpi ära mahtuma ja karpi ei tohi jääda tühja ruumi.)
[Raadionupud]
A. [A,1], [A,2], [B,1], [A,3]
B. [A,3], [C,2], [A,1], [B,2]
C. [B,1], [A,2], [A,3], [C,1]
D. [B,3], [C,2], [B,2], [A,2]
Õige vastus on: A.
Vastuse leidmiseks on kõige lihtsam vaadata, mida masinad iga käsujada korral teevad.
Näiteks vastusevariandis A toodud käsujada [A,1], [A,2], [B,1], [A,3] peale valmistab esimene masin sinisetriibulise kopra, punasetäpilise kopra, sinisetriibulise veduri ja rohelise kopra. Teine masin paneb sinisetriibulise kopra kõrvale, seega pakkimisele jõuavad punasetäpiline kobras, sinisetriibuline vedur ja roheline kobras. Kumbki kobras võtab karbis ruumi 3 ühikut ja vedur 2 ühikut, kokku seega 3+2+3 = 8 ühikut.
Käsujadade mugavamaks uurimiseks on hea tähele panna, et teine masin paneb kõrvale mänguasjad, mille esimene masin valmistab käskude [A,1], [B,2] ja [C,3] peale. Samuti on hea tähele panna, et ruumiühikute arvu, mille mänguasi karbis võtab, määrab selle valmistamise käsus olev täht: A=3, B=2, C=1.
Nii saame kõigi variantide analüüsid panna kirja märksa ülevaatlikumalt:
Variant A: [A,1], [A,2], [B,1], [A,3] → [A,2], [B,1], [A,3] → A+B+A = 3+2+3 = 8 ühikut. Karp saab täpselt täis.
Variant B: [A,3], [C,2], [A,1], [B,2] → [A,3], [C,2] → A+C = 3+1 = 4 ühikut. Karpi jääb 4 ühikut tühja ruumi.
Variant C: [B,1], [A,2], [A,3], [C,1] → [B,1], [A,2], [A,3], [C,1] → B+A+A+C = 2+3+3+1 = 9 ühikut. Ei mahu ühte karpi ära.
Variant D: [B,3], [C,2], [B,2], [A,2] → [B,3], [C,2], [A,2] → B+C+A = 2+1+3 = 6 ühikut. Karpi jääb 2 ühikut tühja ruumi.
Seega ongi A ainuke sobiv vastusevariant.

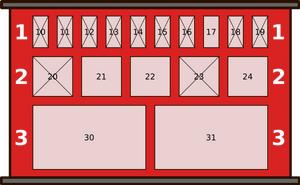
Kopraküla pakiautomaadis võtab robot pakke vastu ja paneb neid kappidesse.
Iga pakk on kas väike, keskmine või suur. Ka kappe on kolme suurust: 1, 2, 3. Väikesed pakid mahuvad kõigisse kappidesse. Keskmised pakid mahuvad kappidesse suurusega 2 või 3. Suured pakid mahuvad ainult kappidesse suurusega 3.
Uue paki saabudes tuvastab robot kaamera abil selle suuruse ja paneb selle kõige väiksema numbriga vabasse kappi, millesse see mahub.
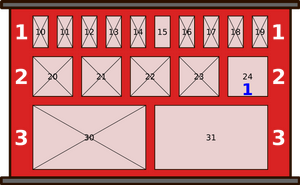
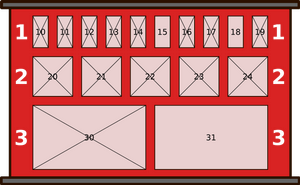
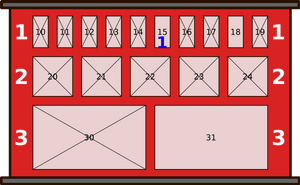
Ühel hommikul on kappide seis selline, nagu näidatud alloleval joonisel. Ristid on peale tõmmatud neile kappidele, kus on juba pakid sees (ja kuhu seetõttu uusi pakke panna ei saa).
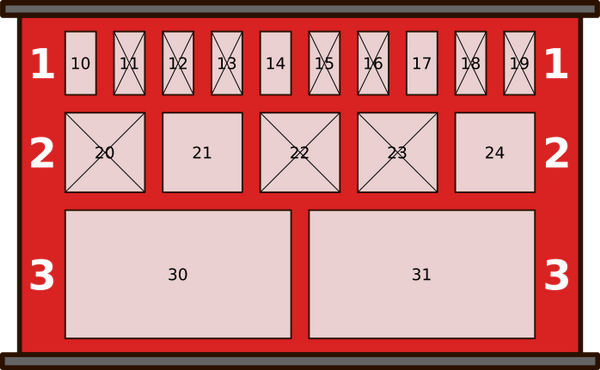
Päeva jooksul toimuvad järgmised kaheksa sündmust:
Millise numbriga kappi pani robot viimasena saabunud paki?
[Täisarv]
Õige vastus on: 15.
Vastuse leidmiseks vaatame, kuidas muutus kappide seis päeva jooksul.
| Sündmus | Tulemus |
|---|---|
|
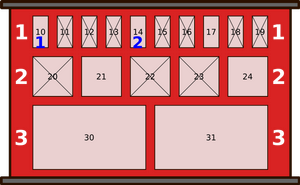
|
|
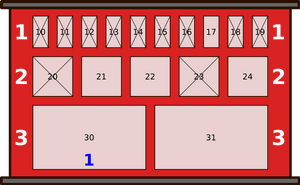
|
|
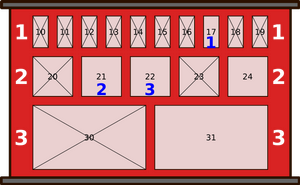
|
|
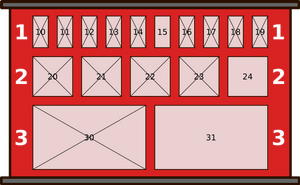
|
|
|
|
|
|
|
|
|

Sel aastal aitavad koprad jõuluvanal kinke valmistada. Nad kasutavad selleks spetsiaalset masinat. Korraga saab masinat kasutada ainult üks kobras, teised peavad ootama.

Kui kobras saabub kinki valmistama, jääb ta kõigepealt ootama. Kui masin vabaneb, läheb ootavate kobraste hulgast kinki valmistama see, kelle kingi valmistamine võtab kõige vähem aega.
Kui üks kobras on kingi valmistamist alustanud, viib ta selle alati lõpule ja alles siis saab järgmine kobras oma kinki valmistama hakata.
Iga kobras valmistab ühe kingi vastavalt järgmisele tabelile.
| Kobras | Kink | Valmistamise aeg | Kopra saabumise aeg |
|---|---|---|---|
| Andres | Auto | 5 minutit | 8:00 |
| Boris | Karu | 10 minutit | 8:00 |
| Chris | Nukk | 7 minutit | 8:04 |
| Diana | Rong | 12 minutit | 8:10 |
| Ene | Klotsid | 9 minutit | 8:10 |
Millises järjekorras koprad oma kingid valmistavad?
[Raadionupud]
A. Andres, Boris, Chris, Diana, Ene
B. Andres, Boris, Chris, Ene, Diana
C. Andres, Chris, Boris, Ene, Diana
D. Andres, Chris, Ene, Boris, Diana
Õige vastus on: D.
Vastavalt masina kasutamise reeglitele toimuvad sündmused järgmiselt.
Kell 8:00 saabuvad Andres ja Boris. Kuna Andrese kingi valmistamise aeg (5 min) on lühem kui Borisi oma (10 min), läheb esimesena masina juurde Andres.
Andres lõpetab oma kingi valmistamise kell 8:05. Selleks ajaks on saabunud ka Chris. Seega on nüüd ootamas Boris ja Chris. Kuna Chrisi kingi valmistamise aeg (7 min) on lühem kui Borisi oma (10 min), läheb järgmisena masina juurde Chris.
Chris lõpetab oma kingi valmistamise kell 8:12. Selleks ajaks on saabunud ka Diana ja Ene. Seega on nüüd ootamas Boris, Diana ja Ene. Kuna Ene kingi valmistamise aeg (9 min) on neist kolmest kõige lühem, läheb järgmisena masina juurde just tema.
Ene lõpetab oma kingi valmistamis kell 8:21. Vahepeal kedagi juurde tulnud ei ole. Seega on nüüd ootamas Boris ja Diana. Borisi kingi valmistamise aeg on lühem ja tema läheb järgmisena masina juurde.
Boris lõpetab oma kingi valmistamise kell 8:31. Vahepeal kedagi juurde tulnud ei ole. Seega on ootamas ainult Diana ja tema lähebki masina juurde.
Diana lõpetab oma kingi valmistamise kell 8:43. Sellega on kõik koprad oma kingid valmistanud.
Nagu näha, on kinkide valmistamise järjekord Andres, Chris, Ene, Boris, Diana, täpselt nagu kirjas vastusevariandis D.

Ühe jõeäärse küla koprad saadavad naaberkülla sõnumeid nii, et kirjutavad puust ketastele igaühele ühe numbri (ühekohalise arvu) ja lasevad kettad allavoolu.

Kettad jõuavad järgmisse külla alati õiges järjekorras, aga vahel juhtub, et veevool keerab mõne ketta kummuli ja sellele kirjutatud numbrit ei ole enam näha.
Selle olukorra lahendamiseks lisavad koprad iga sõnumi lõppu veel ühe ketta ja kirjutavad sellele kontrollnumbri. Kontrollnumber arvutatakse nii, et sõnumis paaritute järjekorranumbriga ketastel olevad arvud korrutatakse kolmega ja paarisnumbritega ketastel olevad arvud ühega. Siis liidetakse korrutised kokku ja võetakse kontrollnumbriks saadud summa viimane number.
Allpool on näha ülaltoodud sõnumi kontrollnumbri arvutus. Ketastel olevad numbrid on paksus kirjas.
| Ketas 1 | Ketas 2 | Ketas 3 | Ketas 4 | Summa | ||||
|---|---|---|---|---|---|---|---|---|
| 8×3 | + | 4×1 | + | 2×3 | + | 5×1 | = | 39 |
Alloleval joonisel näidatud sõnumis on kolmas ketas kummuli läinud.

Mis number sellel kettal oli?
[Täisarv]
Õige vastus on: 6.
Kui tähistame kummuli läinud kettal oleva numbri X, siis saame, et selle sõnumi kontrollnumber peab olema summa 4×3 + 1×1 + X×3 + 7×1 viimane number.
Kui vaatame sõnumi teadaolevaid numbreid, siis nende osa kontrollsummas on 4×3 + 1×1 + 7×1 = 20. Samas teame, et kontrollnumber on 8. See tähendab, et X peab olema selline ühekohaline arv, mille korral X×3 viimane number on 8. Ainuke selline arv on 6.
Seda on lihtne näha, kui kirjutame välja X×3 väärtused kõiki ühekohaliste X väärtuste jaoks:
0×3 = 0, 1×3 = 3, 2×3 = 6, 3×3 = 9, 4×3 = 12, 5×3 = 15, 6×3 = 18, 7×3 = 21, 8×3 = 24, 9×3 = 27.
Seega peab kummuli läinud kettal olema number 6 ja järelikult saatsid koprad teele sõnumi 41678.

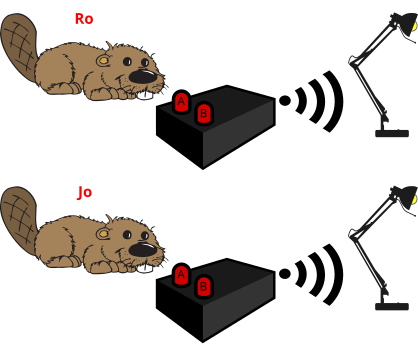
Ro ja Jo leidsid garaažist kaks puldiga juhitavat laualampi. Kummalgi puldil on kaks nuppu, A ja B, mis töötavad vastavalt järgmisele tabelile.
| Nupp A | Nupp B | Lamp |
|---|---|---|
| Väljas | Väljas | Sees |
| Sees | Väljas | Sees |
| Väljas | Sees | Sees |
| Sees | Sees | Väljas |
Hiljem leidsid Ro ja Jo ka puldiga juhitava aialambi. Aialambi puldil on nuppude asemel antennid. Katsetades panid nad tähele, et
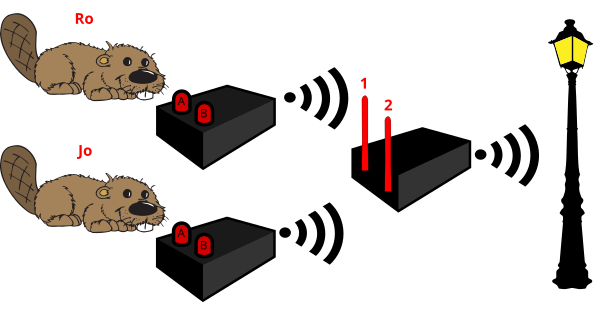
Kui Jo puldil on mõlemad nupud väljas, siis mida peab Ro oma puldil tegema, et aialamp sisse lülitada?
[Raadionupud]
A. Lülitama sisse ainult nupu A
B. Lülitama sisse ainult nupu B
C. Mõlemad nupud sisse lülitama
D. Mõlemad nupud välja lülitama
Õige vastus on: C.
Üks viis selle ülesande lahendamiseks on vaadata läbi kõik võimalikud Ro puldi nuppude olekud ja leida iga variandi kohta, kas aialamp lülitub sisse või välja. Kuna Jo puldi nupud on mõlemad väljas, on aialambi puldi antennis 2 signaal sees. Siis saame Ro puldi nuppude olekuid läbi vaadates järgmised tulemused:
| Ro nupp A | Ro nupp B | Antenn 1 | Antenn 2 | Aialamp |
|---|---|---|---|---|
| Väljas | Väljas | Sees | Sees | Väljas |
| Sees | Väljas | Sees | Sees | Väljas |
| Väljas | Sees | Sees | Sees | Väljas |
| Sees | Sees | Väljas | Sees | Sees |
Teine võimalus on lahendada ülesannet tagantpoolt ettepoole. Selleks, et aialamp sisse lülituks, peab vähemalt ühes tema antennis signaal väljas olema. Kuna Jo puldi mõlemad nupud on väljas, on aialambi puldi antennis 2 signaal sees. Seega on aialambi sisse lülitamiseks vaja, et selle puldi antennis 1 oleks signaal väljas. Oma puldi signaali välja lülitamiseks peab Ro sellel mõlemad nupud sisse vajutama.
Nagu näha, viisid mõlemad lahendusviisid samale järeldusele: ainus õige vastusevariant on C.

Jane on uus Nazca kosmosejaama elukeskkonna süsteemide operaator. Kosmosejaam koosneb kolmest alast, millel on kõigil ühesugused juhtpaneelid. Igal juhtpaneelil on neli hooba, millest üks lülitab sisse kütte, üks valguse, üks õhupuhastuse ja üks veepuhastuse. Kahjuks on kosmosejaam juba väga vana ja hoobade juures olevad kirjad on ära kulunud.
Allolev skeem näitab kosmosejaama kõigi kolme ala elukeskkonna süsteemide ja nende juhtpaneelide olekuid.
| Ala A | Ala B | Ala C |
|---|---|---|
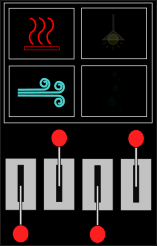 |
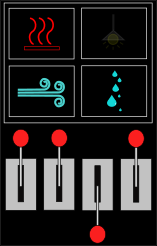 |
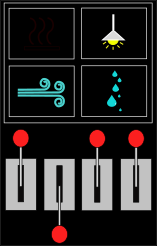 |
Milline hoob juhib millist süsteemi?
[Raadionupud]
A. 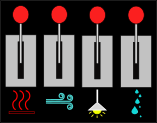
B. 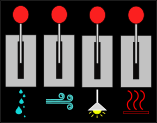
C. 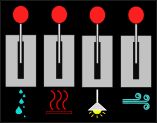
D. 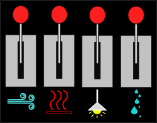
Õige vastus on: C.
Vastuse leidmiseks peame võrdlema erinevusi kosmosejaama erinevate alade süsteemide olekute ja nende juhtpaneelidel olevate hoobade asendite vahel.
Alade A ja B võrdlemisel näeme, et ainsad erinevused on veepuhastussüsteemi olek ja vasakult esimese hoova asend. Seega peab esimese hoova üles lükkamine veepuhastuse sisse lülitama. Sellega sobib ka ala C olek, kus on samuti veepuhastus sisse lülitatud ja esimene hoob üles lükatud.
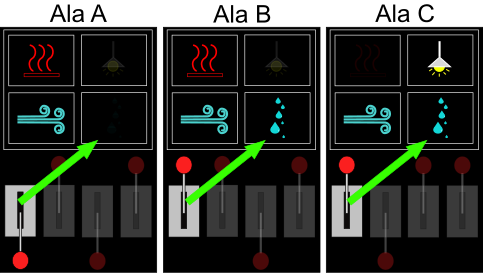
Kõigi kolme ala võrdlemisel näeme, ainus süsteem, mis on kõigis kolmes alas sisse lülitatud, on õhupuhastus. Kuna neljas hoob on ainsana kõigil kolmel paneelil samas asendis, peab see juhtima õhupuhastust.
Edasi näeme, et küte on alades A ja B sees, aga alas C väljas. Samamoodi on teine hoob alade A ja B paneelidel üleval ja ala C paneelil all. Järelikult peab see hoob juhtima küttesüsteemi.
Nüüd on üle jäänud veel valgus, mis on ainsana sisse lülitatud alas C, ja kolmas hoob, mis on samuti ainsana üleval ala C paneelil.
Seega ongi süsteemide ja hoobade vastavus selline, nagu näidatud vastusevariandis C:


|
Anu, Bob ja Carl ostavad sageli oma kooli ees olevast automaadist karastusjooke. Automaat müüb üheksat liiki jooke ja kolmel sõbral on igaühel kolm kindlat lemmikut. Esmaspäeval ostsid jooke ainult Anu ja Bob. Nad ostsid kahepeale joogid 1, 2, 3, 5, 8 ja 9. Teisipäeval ostsid jooke ainult Bob ja Carl. Nemad ostsid kahepeale joogid 1, 4, 5, 6, 7 ja 9. |

|
Millised on Anu lemmikjoogid?
[Raadionupud]
A. 1, 2 ja 3
B. 1, 2 ja 5
C. 2, 3 ja 8
D. 2, 3 ja 9
Õige vastus on: C.
Kuna Bob ostis jooke mõlemal päeval, peavad tema lemmikud olema need, mida osteti mõlemal päeval. Need on 1, 5 ja 9.
Esmaspäeval osteti lisaks veel joogid 2, 3 ja 8. Need pidi ostma Anu ja järelikult ongi need tema lemmikud.

Angela ja Bianca on kohvikus ja nende laual on ilus muster:

Angela ütleb Biancale:
Vaata seda kujundit:
.
Kui seda võib igasse asendisse pöörata, aga mitte peegeldada, siis esineb see kujund meie laua peal kaks korda:
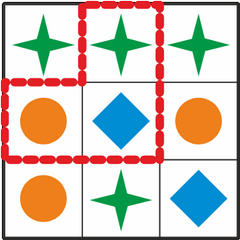
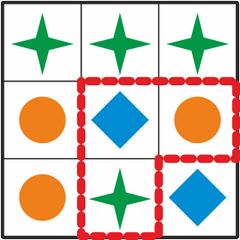
Bianca vastab:
Jah, sul on õigus. Aga vaata nüüd seda suuremat lauda:

Mitu korda sa leiad siit kujundi
?
Milline on õige vastus Bianca küsimusele?
[Täisarv]
Õige vastus on: 4.
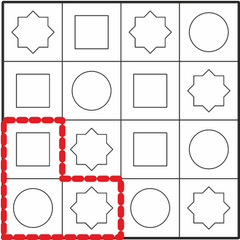
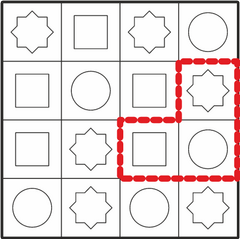
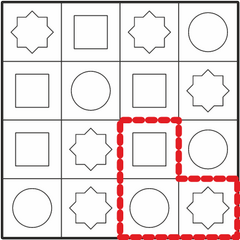
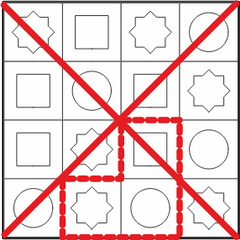
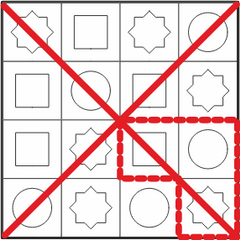
Kõigi õigete vastuste leidmiseks on kasulik panna tähele, et otsitavas kujundis on keskmisel ruudul punane ring. Kui otsime laualt üles kõik punased ringid, oleme leidnud kõik kohad, kus see kujund võib laual olla.
Lisaks peab punase ringi kõrval olema sinine ruut ja sellest päripäeva järgmine roheline kaheksanurk. Nendele lisatingimustele vastavad täpselt neli kujundit:
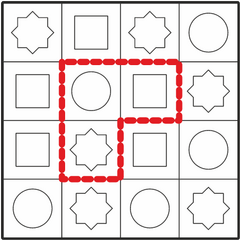
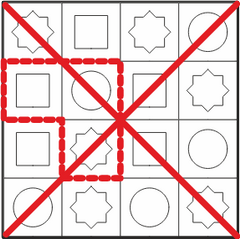
Tuleb olla hoolikas, et mitte kogemata lugeda otsitava kujundi peegelpilte  .
.
Peegelpildis on ka punase ringi kõrval sinine ruut ja roheline kaheksanurk, aga kaheksanurk on ruudust vastupäeva, mitte päripäeva:
Copyright © 2023 Bebras – International Challenge on Informatics and Computational Thinking.
Licensed under Creative Commons Attribution-ShareAlike 4.0 International License.
Flag icons by GoSquared.