

Когда бобры льют краску на пол лабиринта, то каждую секунду она растекается по квадратам, которые находятся по соседству с уже окрашенными квадратами. Как видно на нижеприведённом рисунке, краска растекается только по полу и не просачивается через стенки.
| Начало | 1ая секунда | 2ая секунда | 3ья секунда |
|---|---|---|---|
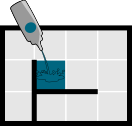 |
 |
 |
 |
Если бобры одновременно льют на пол краски нескольких цветов, то каждый квадрат заполняется цветом той краски, которая достигает его первым. Если краски нескольких цветов одновременно достигают квадрата, то этот квадрат заполняется краской самого тёмного цвета.
| Начало | 1ая секунда | 2ая секунда |
|---|---|---|
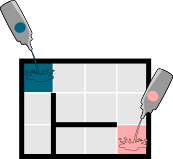 |
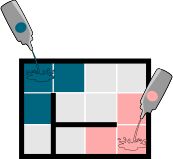 |
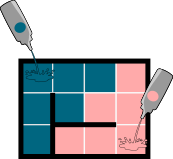 |
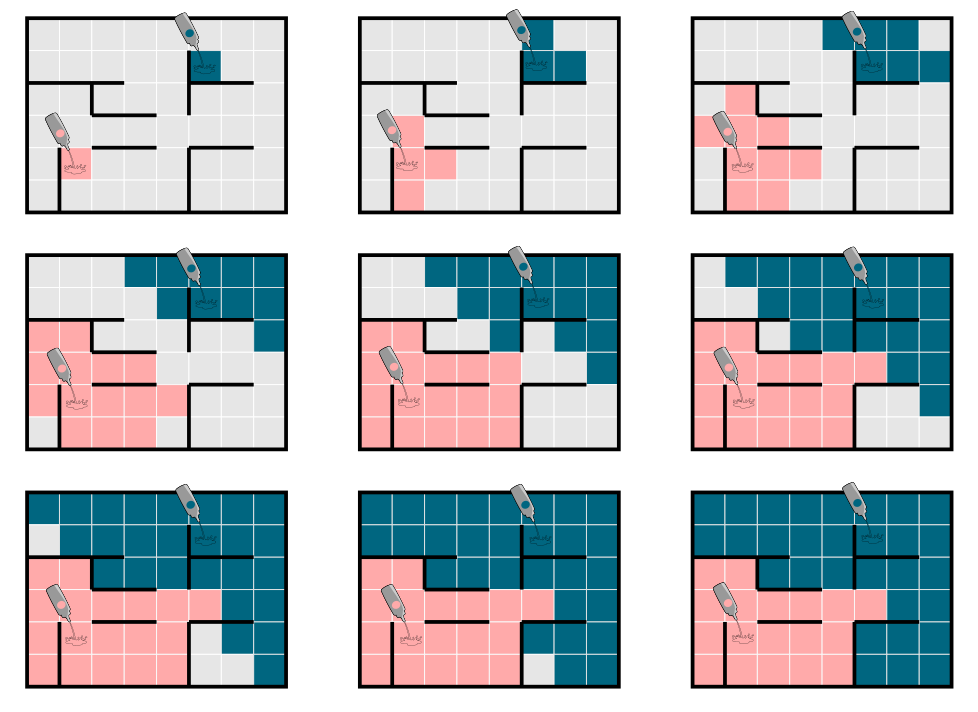
Бобры вылили два цвета на пол нижеприведённого лабиринта.
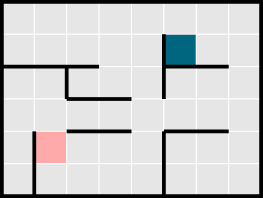
Каков будет результат?
[Raadionupud]
A. 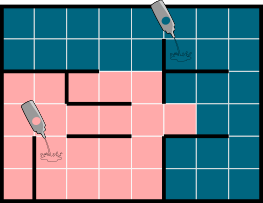 B.
B. 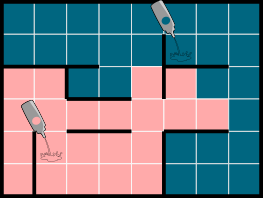 C.
C. 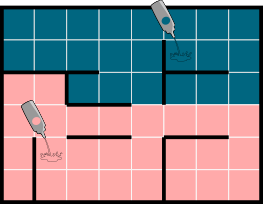 D.
D. 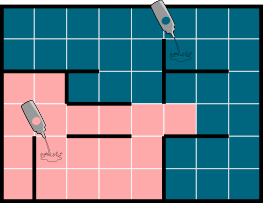
Правильный ответ: D.
Нижеприведённый рисунок показывает растекание красок по секундам.

У Пети есть четыре машины для печати фигур на бумаге:


Петя пропустил лист белой бумаги в некотором порядке через все четыре машины, но через каждую ровно по одному разу, и получил результат как показано на рисунке ниже.

Какая машина напечатала треугольник на бумаге?
[Raadionupud]
A. Машина A
B. Машина B
C. Машина C
D. Машина D
Правильный ответ: D.
Глядя на результат, мы можем обратить внимание на следующие моменты:
Машина, перекрасившая страницу в чёрный цвет, должна была находиться в очереди раньше машины, которая напечатала стрелку; в противном случае стрелка располагалась бы под чёрным цветом и вообще не была бы в результате видна.
Машина, перекрасившая страницу в чёрный цвет, должна была находиться в очереди раньше машины, которая напечатала треугольник; в противном случае треугольник располагался бы под чёрным цветом и вообще не был бы в результате виден.
Машина, переворачивающая страницу на 180 градусов, должна была находиться в очереди после машины, которая напечатала стрелку; в противном случае стрелка была бы в результате направлена вниз.
Машина, переворачивающая страницу на 180 градусов, должна была находиться в очереди раньше машины, которая напечатала треугольник; в противном случае вершина треугольника была бы в результате направлена вниз.
Изучив все эти моменты, можно сделать вывод, что порядок машин должен был быть следующим:
Следовательно, треугольник должна была напечатать последняя находящаяся в очереди машина, то есть машина D.

Павел работает почтальоном в деревне, где живёт пять бобров. Если один из бобров хочет отправить письмо любому другому бобру, то он оставляет это письмо в своём почтовом ящике.
Павел ходит от одного почтового ящика к другому и у каждого ящика выполняет два действия:
Павел начинает свой день с пустой сумкой. Кроме того, он знает, что содержимое почтовых ящиков бобров следующее:

Павел хочет доставить все письма таким образом, чтобы он оказывался у каждого почтового ящика только один раз.
В каком порядке должен Павел обойти почтовые ящики?
[Raadionupud]
A. Галя → Катя → Лёня → Света → Толя
B. Галя → Света → Катя → Толя → Лёня
C. Галя → Катя → Света → Лёня → Толя
D. Катя → Галя → Света → Лёня → Толя
Правильный ответ: C.
Конечно, мы могли бы найти правильный ответ среди предложенных вариантов, просто проверив порядок посещений почтовых ящиков, который записан в каждом варианте. При этом мы всегда должны были бы помнить, какие письма лежат в сумке Павла. Если в конце обхода сумка снова оказалась бы пустой, значит, все письма были бы доставлены получателям. Решая таким образом, мы увидели бы, что
Следовательно, из предложенных вариантов ответов подходит только C.
Второй способ найти решение — это рассуждать следующим образом:
Итак, получается, что указанный в варианте C порядок является единственным возможным решением.

Транспортный департамент Бобруйска ежегодно выдаёт ограниченное количество разрешений на бесплатную парковку. Каждое разрешение имеет код, который соответствует следующим правилам:
Бобры используют обычные цифры (от 0 до 9), но алфавит ротокас, в котором только 12 букв:

На рисунке гласные буквы указаны зелёным цветом и на фоне с точками, согласные — красным цветом и на фоне в полосочку.
В кодах разрешений используются только заглавные буквы; одна буква может встречаться в коде разрешения несколько раз.
Сколько уникальных (с разными кодами) разрешений на парковку может выдать транспортный департамент?
[Täisarv]
Правильный ответ: 4200.
Первый символ кода содержит согласную букву. В алфавите ротокас имеется 7 согласных. Значит, у нас есть 7 способов для выбора первого символа.
Второй символ кода содержит букву, но нет ограничений на то, должна это быть гласная или согласная буква. Значит, у нас есть 12 способов для выбора второго символа.
Третий символ кода содержит гласную букву. В алфавите ротокас имеется 5 гласных. Значит, у нас есть 5 способов для выбора третьего символа.
Последним символом кода является цифра. Для её выбора у нас есть 10 возможностей.
Каждый раз, когда в качестве первого символа мы выбираем одну из семи согласных букв, при добавлении второго символа мы уже получаем 12 разных пар букв. Аналогично, добавив к каждой паре букв разные гласные, мы получим 5 разных комбинаций, состоящих из трёх символов. А добавив к каждой такой комбинации ещё одну из 10 возможных цифр, получим четырёхзначные коды. Таким образом, имеется 7x12x5x10 = 4200 кодов, которые соответствуют правилам.

Дигитальные часы используют светодиодные (LED) индикаторы для отображения цифр. Каждый индикатор имеет семь сегментов, которые можно включать и выключать. На нижеприведённом рисунке показано, как с помощью таких индикаторов отображаются цифры 0 и 2.

В комнате у бобра на стене висят часы, у которых немного сломан самый крайний правый индикатор: один из семи его сегментов не включается.
На нижеприведённом рисунке можно увидеть, что показывали часы последние три минуты.

Что покажут часы в следующую минуту?
[Raadionupud]
A.  B.
B.  C.
C.  D.
D. 
Правильный ответ: B.
На рисунке в тексте задания видно, что в течение трех минут часы правильно отображали значения цифр справа (1, 2, 3). Это значит, что включались сегменты, которые на нижеприведённом рисунке слева отмечены красным. Следовательно, неисправным должен быть сегмент, который отмечен на нижеприведённом рисунке справа.


В следующую минуту часы должны показать 01:14. Если бы индикатор был полностью в порядке, то самая крайняя цифра (4) должна была быть такой, как показано на нижеприведённом рисунке слева. Учитывая, что один сегмент этого индикатора сломан, то результатом будет то, что мы видим на нижеприведённом рисунке справа.


Следовательно, в следующую минуту часы покажут то, что изображено в ответе варианта B.

Робот посылочного автомата принимает посылки и распределяет их по шкафчикам.
Каждая посылка может быть маленькой, средней или большой. Шкафчики тоже могут быть трёх размеров: 1, 2, 3. Маленькие посылки помещаются во все шкафчики. Средние посылки помещаются в шкафчики размером 2 или 3. Большие посылки помещаются только в шкафчики размером 3.
Когда приходит новая посылка, робот с помощью камеры определяет её размер и кладёт её в свободный шкафчик под наименьшим номером, в который эта посылка может поместиться.
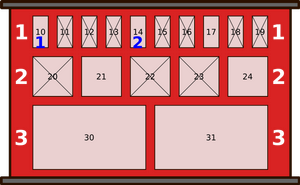
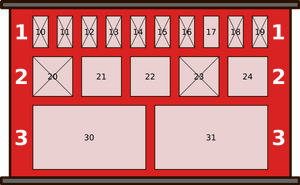
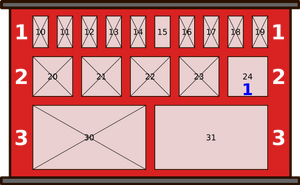
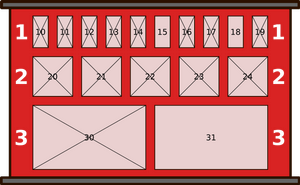
Однажды утром состояние шкафчиков было таким, как показано на нижеприведённом рисунке. Крестики имеются на тех шкафчиках, внутри которых уже есть посылки (и куда, следовательно, нельзя положить новые посылки).
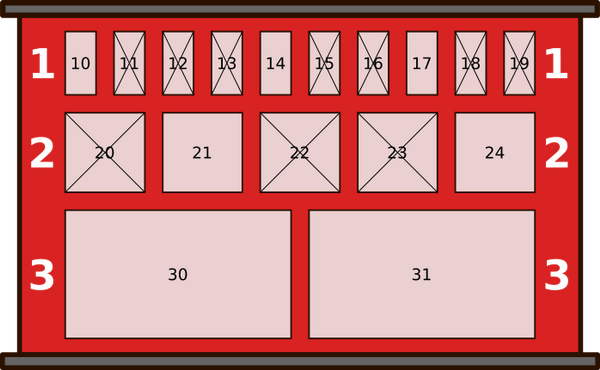
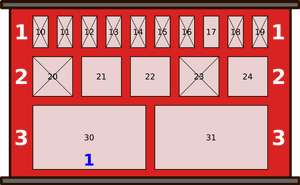
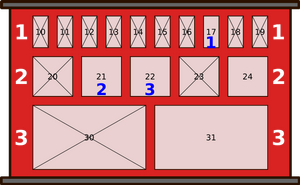
В течение дня происходят следующие восемь событий:
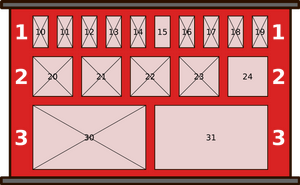
В шкафчик под какие номером робот положит пришедшую последней посылку?
[Täisarv]
Правильный ответ: 15.
Чтобы найти ответ, давайте посмотрим, как менялось состояние шкафчиков в течение дня.
| Событие | Результат |
|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
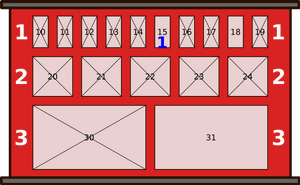
|

Правительство Республики Кастории хранит свои секретные документы в конвертах и в специальном шкафу. Всего имеется 16 конвертов, и они пронумерованы от 1 до 16. Правительство уже открыло 10 конвертов, но 6 ещё вчера были запечатаны.
Однако ночью в здание правительства прокрался шпион и вскрыл ещё один конверт, и теперь в шкафу 11 открытых конвертов:

Хранитель документов не помнит точно, какие именно конверты были уже открыты правительством, но помнит, что
Какой конверт вскрыл шпион?
[Raadionupud]
A. Конверт под номером 5
B. Конверт под номером 9
C. Конверт под номером 10
D. Конверт под номером 13
E. Имеющейся информации недостаточно для ответа на вопрос
Правильный ответ: D.
Чтобы найти решение, мы можем рассуждать следующим образом:
Сейчас всего в столбцах С2 и С4 имеется чётное количество открытых конвертов, именно так, как помнит хранитель. Поскольку шпион вскрыл только один конверт, то он должен находиться либо в столбце C1, либо в столбце C3.
Сейчас всего в столбцах С3 и С4 имеется чётное количество открытых конвертов, именно так, как помнит хранитель. Учитывая предыдущий пункт, это значит, что вскрытый шпионом конверт должен находиться в столбце C1.
Сейчас всего в строках R2 и R4 имеется нечётное количество открытых конвертов, а это не соответствует тому, что помнит хранитель. Это значит, что вскрытый конверт должен находиться в строке R2 или в строке R4.
Сейчас всего в строках R3 и R4 имеется нечётное количество открытых конвертов, а это не соответствует тому, что помнит хранитель. Учитывая предыдущий пункт, это значит, что вскрытый шпионом конверт должен находиться в строке R4.
Следовательно, шпион вскрыл конверт, который располагается в шкафу в столбце C1 и в строке R4, то есть конверт под номером 13.

Бобры одной прибрежной деревни отправляют сообщения в соседнюю деревню, записывая на каждом деревянном диске по одной цифре (однозначное число) и бросая диски вниз по течению.

Диски всегда доходят до соседней деревни в правильном порядке, но иногда течение воды переворачивает один диск вверх дном, и поэтому написанная на нём цифра становится не видной.
Чтобы решить эту проблему, бобры добавляют в конец каждого сообщения еще один диск и пишут на нём контрольную цифру. Контрольная цифра вычисляется путём умножения записанных в сообщении на нечётных дисках цифр на три, а цифр на чётных дисках на единицу. Затем произведения складываются и последняя цифра полученной суммы принимается за контрольную.
Ниже показано вычисление контрольной цифры для вышеприведённого сообщения. Цифры на дисках выделены полужирным шрифтом.
| Диск 1 | Диск 2 | Диск 3 | Диск 4 | Сумма | ||||
|---|---|---|---|---|---|---|---|---|
| 8×3 | + | 4×1 | + | 2×3 | + | 5×1 | = | 39 |
В сообщении на нижеприведённом рисунке третий диск перевёрнут вверх дном.

Какая цифра была на этом диске?
[Täisarv]
Правильный ответ: 6.
Если отметим с помощью Х цифру, которая была на перевернутом диске, то получим, что контрольная цифра этого сообщения должна быть последней цифрой суммы 4×3 + 1×1 + X×3 + 7×1.
Если мы посмотрим на известные цифры сообщения, то их часть в контрольной сумме равна 4×3 + 1×1 + 7×1 = 20. При этом мы знаем, что контрольная цифра равна 8. Это значит, что X должен быть таким однозначным числом, в результате чего X × 3 даст нам последнюю цифру 8. Единственное такое число — 6.
В этом легко убедиться, если записать значения X×3 для всех однозначных значений X:
0×3 = 0, 1×3 = 3, 2×3 = 6, 3×3 = 9, 4×3 = 12, 5×3 = 15, 6×3 = 18, 7×3 = 21, 8×3 = 24, 9×3 = 27.
Следовательно, на перевёрнутом диске должна быть цифра 6, а отправленное сообщение было 41678.

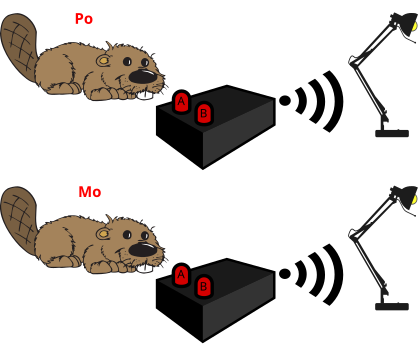
Ро и Мо нашли в гараже две настольные лампы, управляемые с помощью пультов. На каждом пульте имеется по две кнопки, A и B, которые работают в соответствии со следующей таблицей.
| Кнопка A | Кнопка B | Лампа |
|---|---|---|
| Выключена | Выключена | Включена |
| Включена | Выключена | Включена |
| Выключена | Включена | Включена |
| Включена | Включена | Выключена |
Позже Ро и Мо также фонарь, который также управляется с помощью пульта. Но на пульте от фонаря вместо кнопок располагаются антенны. Экспериментируя, они заметили, что
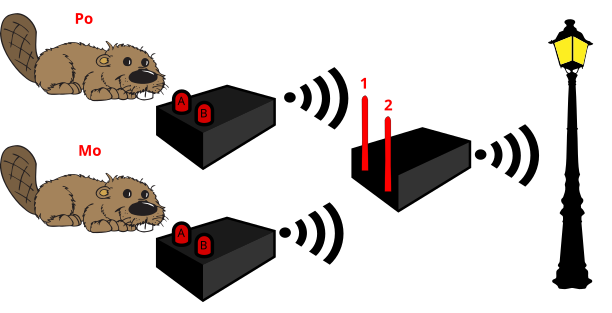
Если обе кнопки на пульте Мо выключены, то что должен Ро сделать на своём пульте, чтобы включить фонарь?
[Raadionupud]
A. Включить только кнопку A
B. Включить только кнопку B
C. Включить обе кнопки
D. Выключить обе кнопки
Правильный ответ: C.
Один из способов решения этого задания — перебрать все возможные состояния кнопок на пульте Ро и для каждого варианта проверить, включается или выключается фонарь. Поскольку обе кнопки на пульте Мо выключены, то сигнал на антенне 2 пульта от фонаря включён. Тогда, просмотрев состояния кнопок на пульте Ро, получим следующие результаты:
| Кнопка А у Ро | Кнопка B у Ро | Антенна 1 | Антенна 2 | Фонарь |
|---|---|---|---|---|
| Выключена | Выключена | Включена | Включена | Выключен |
| Включена | Выключена | Включена | Включена | Выключен |
| Выключена | Включена | Включена | Включена | Выключен |
| Включена | Включена | Выключена | Включена | Включён |
Другой способ — решить задание с конца. Чтобы фонарь включился, необходимо, чтобы хотя бы одна из антенн была выключена. Поскольку обе кнопки на пульте Мо выключены, то сигнал на антенне 2 пульта от фонаря включён. Поэтому, чтобы включить фонарь, необходимо, чтобы сигнал на антенне 1 пульта от фонаря был выключен. Чтобы выключить сигнал на своем пульте, Ро должен включить на нем обе кнопки.
Как видно, оба способа привели нас к одному и тому же выводу: единственно верным вариантом ответа будет C.

Сегодня состоится ежегодный турнир среди бобров. В турнире примут участие 16 бобров. Турнир состоит из четырёх туров. В первом туре все 16 бобров соревнуются вместе, но далее их пути расходятся. Победители каждого тура проходят в следующий тур (или на своё место в итоговой таблице), как показывает направление левой стрелки, а проигравшие двигаются в направлении правой стрелки.
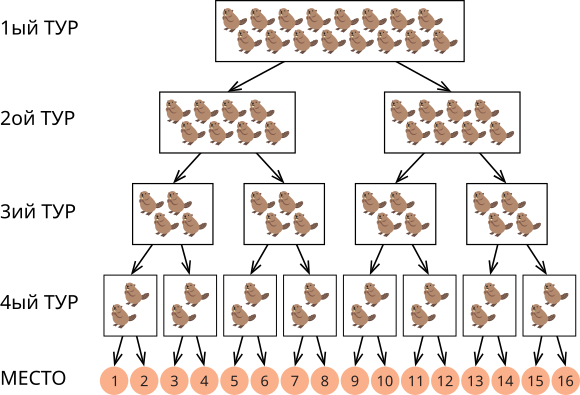
Например, бобр, который выиграет в 1ом и 2ом турах, но проиграет в 3ем и 4ом турах, в итоге получит 4ое место.
Норо один из участников турнира. Какое место он может получить, если проиграет только один тур?
(Отметь все правильные ответы.)
[Märkeruudud 1..16]
Правильный ответ: 2ое, 3ье, 5ое или 9ое место.
Поскольку турнир состоит из четырёх туров, и Норо проиграет только один тур, то имеется четыре возможных сценария:
Он проиграет в 1ом туре и выиграет в трёх других турах. Тогда, следуя схеме, он будет двигаться "направо, налево, налево, налево" и получит 9ое место.
Он проиграет во 2ом туре и выиграет в трёх других турах. Тогда, следуя схеме, он будет двигаться "налево, направо, налево, налево" и получит 5ое место.
Он проиграет в 3ем туре и выиграет в трёх других турах. Тогда, следуя схеме, он будет двигаться "налево, налево, направо, налево" и получит 3ье место.
Он проиграет в 4ом туре и выиграет в трёх других турах. Тогда, следуя схеме, он будет двигаться "налево, налево, налево, направо" и получит 2ое место.

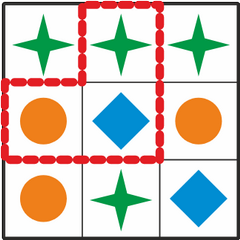
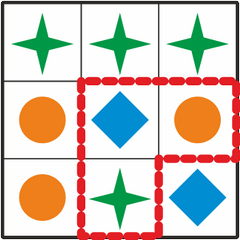
Анжела и Белла пришли в кафе и сели за стол с красивым узором:

Анжела говорит Белле:
Посмотри на эту фигуру:
.
Если её можно вертеть в любом направлении, но не зеркально, то на нашем столе эту фигуру можно увидеть дважды:
Белла отвечает:
Да, ты права. А посмотри вот на этот стол побольше:

Сколько раз ты найдёшь здесь фигуру
?
Какой правильный ответ на вопрос Беллы?
[Täisarv]
Правильный ответ: 4.
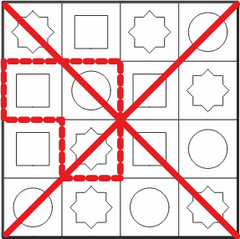
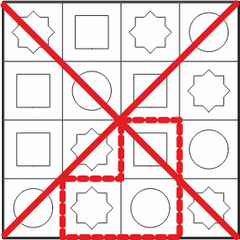
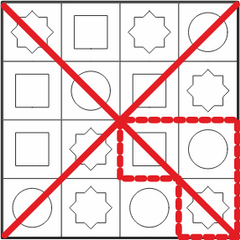
Все правильные ответы (фигуры) можно найти, если заметить, что средний квадрат в искомой фигуре имеет красный круг. Если мы найдём на столе все красные круги, то мы найдём и все места, где эта фигура может находиться на столе.
Кроме того, рядом с красным кругом должен быть синий квадрат, а следуя по часовой стрелке от него и зелёный восьмиугольник. Этим дополнительным условиям соответствуют только четыре фигуры:
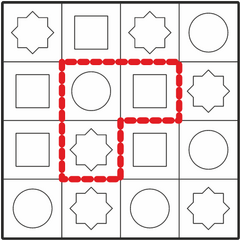
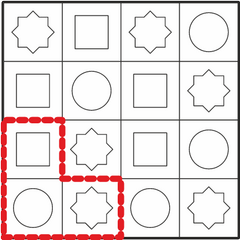
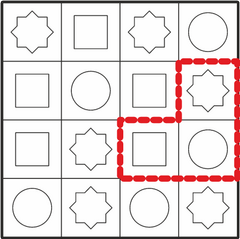
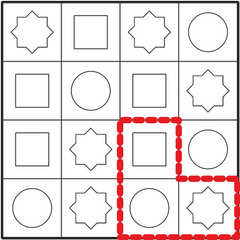
Необходимо быть внимательным, чтобы случайно не посчитать за правильные ответы и зеркальные отображения искомой формы  .
.
В зеркальном отображении рядом с красным кругом также есть синий квадрат и зелёный восьмиугольник, но восьмиугольник расположен против часовой стрелки от квадрата, а не по часовой:

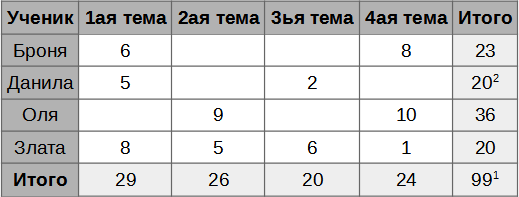
В течение учебного года ученики писали сочинения по четырём темам. Учитель оценивал каждую работу по 10-балльной системе и, прежде чем вернуть работы ученикам, записывал их оценки в свою таблицу.
В конце года он подсчитал сумму оценок каждого ученика и сумму оценок, полученных по каждой теме. Но потом он случайно опрокинул чашку с чаем на таблицу, и некоторые оценки исчезли.
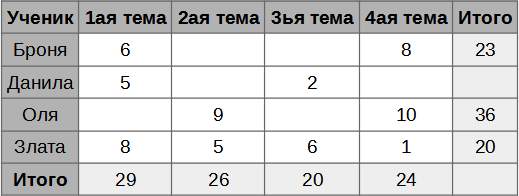
Какова была сумма оценок у Данилы?
[Täisarv]
Правильный ответ: 20.
Чтобы найти решение, мы можем восстановить исчезнувшие оценки одну за другой. Для этого необходимо найти строку или столбец, где не хватает только одной оценки, и посмотреть, какой она должна быть, чтобы в этой строке или столбце получилась правильная сумма. Например, мы можем найти оценку Оли за первую тему: 6 + 5 + x + 8 = 29 ⇒ x = 10.
Затем мы найдём следующую строку или столбец, где есть только один недостающий элемент. Таким образом мы можем восстановить всю таблицу, как показано на нижеприведённом рисунке (индексы показывают одну из возможных последовательностей вычислений).
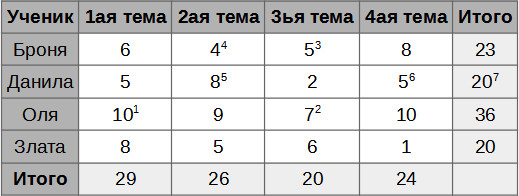
Но есть и хитрый трюк, позволяющий сократить объём работы. Если мы сложим числа в последней строке таблицы (суммы оценок по темам), то получим сумму всех оценок всех учеников. То же самое относится и к последнему столбцу таблицы. А это значит, что суммы последней строки и последнего столбца таблицы должны быть равны. Таким образом, мы сможем восстановить сумму оценок Данилы всего за два шага.

В простом текстовом редакторе при нажатии на клавишу с буквой соответствующая буква добавляется слева от курсора, а также можно использовать некоторые специальные клавиши, которые показаны ниже.

|
Клавиша "←" перемещает курсор на одну букву влево. |

|
Клавиша "→" перемещает курсор на одну букву вправо. |

|
Клавиша "bksp" удаляет букву, которая находится слева от курсора. |

|
Клавиша "del" удаляет букву, которая находится справа от курсора. |

|
Клавиша "home" перемещает курсор в начало строки. |

|
Клавиша "end" перемещает курсор в конец строки. |
Из-за ошибок в связи при передаче текста "abcdefghijklm" одна буква была заменена на звёздочку "*".

Каково наименьшее количество нажатий на клавиши позволит восстановить первоначальный текст?
[Raadionupud]
A. 7
B. 8
C. 9
D. 10
Правильный ответ: B.
Чтобы исправить ошибку, нам сначала потребуется переместить курсор к звёздочке, затем удалить звёздочку, а потом уже ввести правильную букву. К звёздочке мы можем переместиться с помощью клавиши "←". Нажав на неё 7 раз, курсор окажется справа от буквы. Далее, нажав на клавишу "bksp", мы удалим звёздочку, а, нажав на клавишу "f", мы введём правильную букву. Итого нам понадобится 9 нажатий на клавиши.
Второй вариант — это с помощью клавиши "home" переместиться в начало строки, а далее, нажав на клавишу "→", переместиться к звёздочке. Нажав на клавишу "→" 6 раз, курсор окажется слева от звёздочки. Далее, нажав на клавишу "del", мы удалим звёздочку, а, нажав на клавишу "f", мы введём правильную букву. Итого нам понадобится 8 нажатий на клавиши.
Должно быть понятным, что все другие возможные решения потребуют лишних (по сравнению с этими двумя решениями) нажатий на клавиши, и поэтому не являются оптимальными.

Бобры используют следующий метод для сжатия картинок:
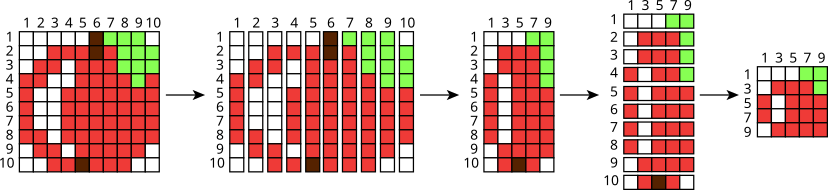
Первым делом они разрезают картинку вертикально на десять полосок одинаковой ширины. Далее они склеивают полоски с нечётными номерами в новую картинку.
После этого они разрезают уже новую картинку горизонтально на десять полосок одинаковой ширины. Затем они склеивают полоски с нечётными номерами и получают итоговую картинку.
Каков будет результат, если нижеприведённую картинку сжать с помощью этого метода?
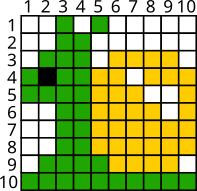
[Raadionupud]
A. 
B. 
C. 
D. 
Правильный ответ: D.
Пошаговое применение метода выглядит следующим образом:
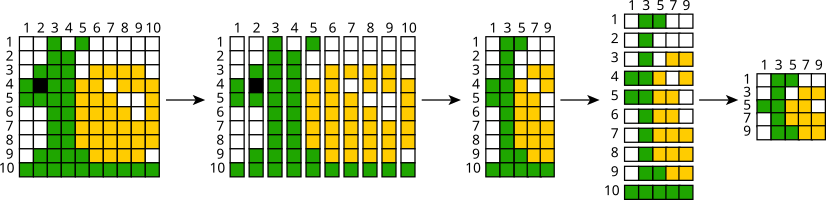

|
Тебе хочется поделиться с друзьями своими фотографиями с отпуска. Ты обдумываешь разные варианты как это сделать и хочешь учесть влияние каждого варианта на окружающую среду. Один из способов измерения влияния на окружающую среду основывается на количестве выбросов CO2:
У тебя 10 фотографий с отпуска, каждая размером примерно по 3МБ, и тебе хочется поделиться ими с 5 друзьями. Чтобы это сделать, у тебя есть три возможных плана: План 1: Отправить фотографии отдельно каждому другу, используя сообщения SnapChat'а. Через сутки сообщения автоматически удалятся. План 2: Создать группу в SnapChat'е, чтобы поделиться фотографиями с 5 друзьями. Далее отправить фотографии с помощью групповых сообщений, которые также через сутки автоматически удалятся. План 3: Загрузить фотографии на общий диск в облаке, отправить всем друзьям сообщения с адресом общего диска и через год удалить фотографии с общего диска. |

|
Какой из нижеприведённых вариантов верно показывает отношения между описанными планами по количеству выбросов CO2?
[Raadionupud]
A. План 1 < План 3 < План 2
B. План 2 < План 3 < План 1
C. План 2 < План 1 < План 3
D. План 3 < План 1 < План 2
Правильный ответ: B.
Чтобы найти ответ, проще всего посчитать количество выбросов CO2 для каждого плана:
План 1: загрузка 10 фотографий (10 × 45гр) и их скачивание одним другом (10 × 45g) в итоге приведут к примерно 450гр + 450гр = 0,9кг CO2. Повторение этого процесса каждым из друзей по отдельности приведёт в итоге к 5 × 0,9кг = 4,5кг CO2. (Количество выбросов CO2, вызванное хранением фотографий в течение одних суток на сервере SnapChat'а, можно считать ничтожно малым по сравнению с предыдущими вычислениями, и это значение можно не учитывать.)
План 2: загрузка 10 фотографий (10 × 45гр) и их скачивание 5 друзьями (5 × 10 × 45гр) приведёт к примерно 450гр + 2250гр = 2,7гр CO2. (Количество выбросов CO2, вызванное хранением фотографий в течение одних суток на сервере SnapChat'а, можно считать ничтожно малым по сравнению с предыдущими вычислениями, и это значение можно не учитывать.)
План 3: загрузка 10 фотографий (10 × 45гр), их хранение в течение года (10 × 60гр) и их скачивание 5 друзьями (5 × 10 × 45гр) приведут к примерно 450гр + 600гр + 2250гр = 3,3гр CO2. (Количество выбросов CO2, вызванное отправкой 5 коротких сообщений, можно считать ничтожно малым по сравнению с предыдущими вычислениями, и это значение можно не учитывать.)
Copyright © 2023 Bebras – International Challenge on Informatics and Computational Thinking.
Licensed under Creative Commons Attribution-ShareAlike 4.0 International License.
Flag icons by GoSquared.