1. Šabloon

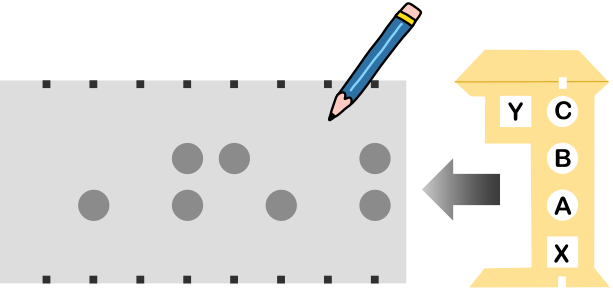
Joonisel näidatud viie auguga (A, B, C, X, Y) šablooni ja pliiatsit kasutatakse järgmiselt:

Liiguta šabloon paberi parempoolsema veeru kohale.
Kui šablooni aukudest A, B ja C paistab paaritu arv halle ringe, värvi šablooni auku X ruut.
Kui šablooni aukudest A, B ja C paistab kaks või rohkem halli ringi, värvi šablooni auku Y ruut.
Liiguta šabloon ühe veeru võrra vasakule. (Pane tähele, et kui šabloon edasi liigub, paistab varem auku Y värvitud ruut läbi augu C ringina.)
Korda eelnevaid samme, kuni šabloon jõuab paberi vasakpoolseima veeru kohale.

Näiteks ülaloleval joonisel kujutatud paberi töötlemise tulemus on selline:

Küsimus

Milline on tulemus, kui samamoodi töödeldakse allolevat paberit?

[Raadionupud]

Vastus

Õige vastus on: C.

Vastuse selgitus

Õige vastuse leidmiseks on kõige lihtsam ülesande tekstis kirjeldatud algoritm läbi teha, kas mõttes või paberil.

2. Küberaed

Küberaias kasvavad lilled ruudukujulistes lahtrites.
Iga lahter võib olla kas valge (tühi) või värviline
(lilli täis).

Igal lahtril on 8 naabrit. Näiteks kõrvaloleval joonisel
on kõik 8 valget lahtrit keskmise värvilise lahtri naabrid.

Küberaed areneb järgmiste reeglite järgi:

Kui värvilisel lahtril on vähem kui kaks värvilist naabrit, muutub see lahter järgmisel päeval valgeks.
Kui värvilisel lahtril on kaks või kolm värvilist naabrit, jääb see lahter ka järgmisel päeval värviliseks.
Kui värvilisel lahtril on rohkem kui kolm värvilist naabrit, muutub see lahter järgmisel päeval valgeks.
Kui valgel lahtril on täpselt kolm värvilist naabrit, muutub see lahter järgmisel päeval värviliseks.

Vaatame näidet:

1. päev	2. päev

Keskmise rea vasakpoolseim lahter muutus valgeks 1. reegli järgi.
Keskmise rea kaks keskmist lahtrit muutusid valgeks 3. reegli järgi.
Kolm ülejäänud värvilist lahtrit jäid värviliseks 2. reegli järgi.
Parempoolseima veeru ülemine ja alumine lahter muutusid värviliseks 4. reegli järgi.

Küsimus

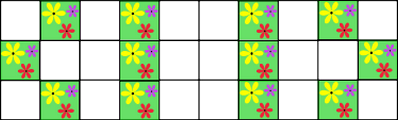
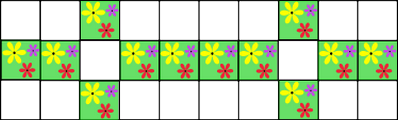
Kui palju värvilisi lahtreid on allolevas aias järgmisel päeval?

(Väljaspool aeda värvilisi lahtreid ei ole.)

[Täisarv]

Vastus

Õige vastus on: 12.

Vastuse selgitus

Rakendades aia kõigile ruutudele nelja eeltoodud reeglit, saame:

3. Autonumbrid

Erinevates riikides on autonumbritel kasutusel erinevad tähtede ja numbrite mustrid. Üldiselt kasutatakse autonumbrites inglise tähestiku suurtähti (mida on 26) ja numbreid (mida on muidugi 10).

Küsimus

Millises alltoodud riikidest on võimalik välja anda kõige rohkem erinevaid autonumbreid?

Vastamisel eeldada, et kõik autonumbrid selles riigis on sama tähtede/numbrite mustriga kui vastusevariandis toodud näide. Täpsemalt, kui näites on mingis kohas täht, siis võib selle riigi autonumbrites selles kohas olla ükskõik milline täht (aga mitte number), ja samamoodi ka numbrite korral. Arvestada ainult valgel taustal olevaid suuri tähti ja numbreid, mitte riigikoodides või vappidel olevaid.

[Raadionupud]

A. (Soome)

B. (Slovakkia)

C. (Rumeenia)

D. (Šveits)

E. (Ukraina)

Vastus

Õige vastus on: E.

Vastuse selgitus

Vastamiseks peame leidma igas riigis võimalike erinevate autonumbrite arvud. Selleks omakorda piisab, kui loeme kokku mitu tähte ja mitu numbrit selle riigi autonumbrites on. Kuna iga tähe valimiseks on 26 ja iga numbri valimiseks 10 võimalust, siis saame järgmised tulemused:

A. 3 tähte ja 3 numbrit: 26³ × 10³;

B. 4 tähte ja 3 numbrit: 26⁴ × 10³;

C. 5 tähte ja 2 numbrit: 26⁵ × 10²;

D. 2 tähte ja 6 numbrit: 26² × 10⁶;

E. 4 tähte ja 4 numbrit: 26⁴ × 10⁴.

Nende arvude välja arvutamine oleks üsna tülikas, aga seda pole ka vaja. Nimelt saame paljudel juhtudel vaadata kahe arvu jagatist ja seal sarnased liikmed välja taandada:

B / A = (26⁴ × 10³) / (26³ × 10³) = 26 > 1 (järelikult B > A);

C / B = 26/10 > 1 (järelikult C > B);

E / C = 10²/26 = 100 / 26 > 1 (järelikult E > C);

E / D = 26²/10² = (26/10)² > 1 (järelikult E > D).

4. Teede kaardistamine

Digiatlaseid valmistav firma tahab koguda pilte kõigist
alloleval kaardil näidatud teedest.

Firma autol kulub iga tee pildistamiseks üks tund ja firma
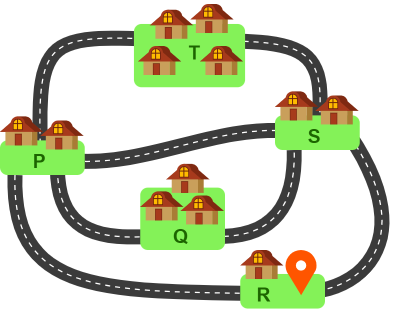
tahab kõik seitse teed pildistada seitsme tunniga.

Küsimus

Mitu erinevat marsruuti on külast R alustaval autol valida, et töö seitsme tunniga tehtud saaks?

[Raadionupud]

A. 6

B. 8

C. 10

D. 12

Vastus

Õige vastus on: D.

Vastuse selgitus

Kõigi teede seitsme tunniga pildistamiseks peab auto iga teed läbima täpselt ühe korra.

See tähendab, et valikuvõimalused on ainult külades R, P ja S. Kuna küladest T ja Q tuleb alati otse läbi sõita, siis need võimalike marsruutide arvu ei mõjuta ja me võime neid mitte arvestada. Seega saame koostada teedevõrgust lihtsustatud skeemi:

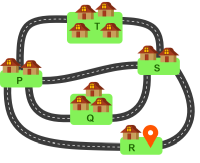
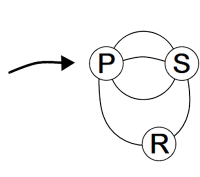
Kui auto alustab külast R, siis peab ta külas R ka lõpetama.

Oletame, alguses liigub auto külast R paremale. Siis jõuab ta külla S ja seal on võimalik valida, mis järjekorras kaardistada külade S ja P vahel olevad teed, aga külast P külla R viiv tee tuleb kaardistada viimasena.

Esimest korda külast S külla P sõitmiseks on valida kolme tee (alumine, keskmine, ülemine) vahel. Külast P külla S tagasi sõitmiseks on valida juba ainult kahe tee vahel, sest tuldud teed tagasi minnes kulutaks auto asjata aega. Teist korda külast S külla P sõites enam valikut ei ole; alati tuleb valida see tee, mis kahe eelmise sõidu järel veel kaardistamata on. Kokku on seega külast S külla P liikudes kõigi kolme tee kaardistamiseks 3 x 2 x 1 = 6 võimalust.

Seega on külast R paremale liikudes kõigi teede optimaalse ajaga kaardistamiseks 6 võimalust. Analoogiliselt arutades jõuame järeldusele, et külast R vasakule liikudes on samuti 6 võimalust.

Seega kokku ongi 12 võimalust.

5. Majade värvimine

Koprakülla ehitati üheksa uut maja. Külavanem otsustas, et uutest majadest kolm tuleb värvida kollaseks, kolm punaseks ja kolm siniseks. Veel otsustas ta, et mitte mingid kaks omavahel teelõiguga ühendatud maja ei tohi olla sama värvi.

Küsimus

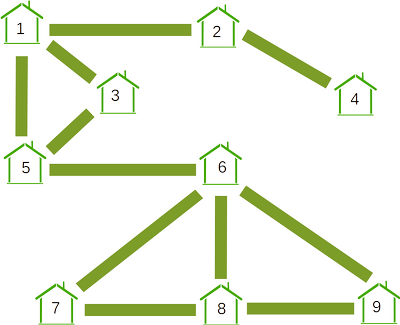
Millised kaks maja värvitakse kindlasti sama värvi?

[Märkeruudud]

A. Maja number 1

B. Maja number 2

C. Maja number 3

D. Maja number 4

E. Maja number 5

F. Maja number 6

G. Maja number 7

H. Maja number 8

I. Maja number 9

Vastus

Õige vastus on: G ja I (majad 7 ja 9).

Vastuse selgitus

Majad 7 ja 9 peavad kindlasti olema sama värvi: majad 6 ja 8 on omavahel ühendatud ja peavad seega olema erinevat värvi; maja 7 on ühendatud nende mõlemaga ja peab seega olema kolmandat värvi; sama kehtib ka maja 9 kohta.

Aga kuidas veenduda, et need on ainukesed majad, mis peavad tingimata sama värvi olema? Vaatleme kolme järgmist värvimist, mis kõik vastavad külavanema nõudmistele:

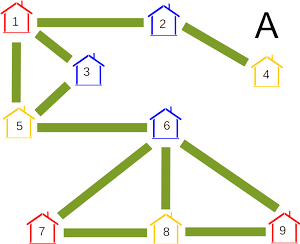
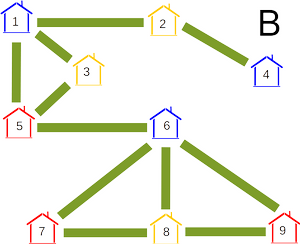
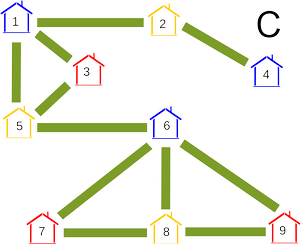
Vaatame esiteks maju 1, 2, 3, 4, 5. Variandis A on samavärvilised paarid {2, 3} ja {4, 5}. Aga need paarid on mõlemad variandis C erivärvilised.

Vaatame nüüd maju 6, 7, 8, 9. Siin grupis on kõigis kolmes variandis kõik paarid peale {7, 9} erivärvilised.

Viimaks vaatame paare, mille üks liige on grupist 1–5 ja teine grupist 6–9. Siin võime tähele panna, et majade 6–9 värvid on variantides A ja B samad, aga majade 1–5 värvid on erinevad. Seega on iga selline paar erivärviline vähemalt ühes neist kahest variandist.

Seega polegi rohkem paare peale majade 7 ja 9, mis kõigis võimalikes värvimisviisides samavärvilised oleks.

6. Digikell

Digikell kasutab numbrite näitamiseks LED-indikaatoreid. Igal indikaatoril on seitse segmenti, mida saab lülitada sisse ja välja. Alloleval joonisel on näha, kuidas selliste indikaatoritega kujutatakse numbreid 0 kuni 9.

Indikaatorite segmendid kuluvad, kui nad põlevad. See segment, mis nädala jooksul kõige rohkem põleb, kulub kõige kiiremini, ja tuleb esimesena välja vahetada.

Küsimus

Milline 28-st segmendist tuleb esimesena välja vahetada?

(Kirjuta vastuseks üks number ja üks täht, nagu alloleval joonisel.)

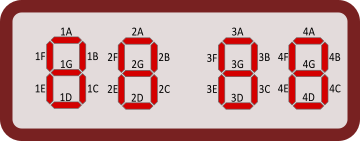
[Tekstikast]

Vastus

Õige vastus on: 1B.

Vastuse selgitus

Kell töötab ja näitab aega 24 tundi ööpäevas. See toimub nädala igal päeval samamoodi. Seega võime selle ülesande lahendamiseks nädala asemel sama hästi uurida, mis juhtub ööpäeva jooksul.

Ööpäeva jooksul näitab kell aegu 00:00 kuni 23:59. Näitest 04:01 on näha, et ühekohalisi arve näitab kell samuti kahekohalisena, lisades arvu algusse nulli.

Tundide kümneliste kohal esinevad kõigis kellaaegades ainult numbrid 0, 1 ja 2. Kõigis neis kolmes numbris on kasutusel segment B. See tähendab, et tundide kümneliste indikaatori segment B põleb ööpäevaringselt, kordagi kustumata.

See on ka ainus ööpäevaringselt põlev segment. Selles veendumiseks vaatame numbreid 1, 2 ja 5. Numbris 1 põlevad ainult segmendid B ja C. Aga numbris 2 ei põle segment C ja numbris 5 ei põle segment B. Kuna tundide ühelised ning minutite kümnelised ja ühelised kasutavad kõik numbreid 1, 2 ja 5, siis on kõigis neis indikaatorites iga segment vähemalt mingi osa ööpäevast välja lülitatud.

7. Õunakorv

Grupp inimesi püüab tagada, et korvis oleks täpselt 10 õuna.

Kui keegi neist vaatab korvi, toimib ta vastavalt sellele, mida ta korvis näeb:

Korvi sisu	Tegevus
Vähem kui 10 õuna	Lisab korvi ühe õuna
Rohkem kui 10 õuna	Eemaldab korvist ühe õuna
Täpselt 10 õuna	Ei tee midagi

Õunte loendamine toimub hetkeliselt, ilma aega kulutamata. Aga õuna korvi lisamine või selle sealt eemaldamine võtab 5 sekundit.

Inimesed üksteisega ei suhtle. Igaüks vaatab korvi ja teeb 5 sekundit hiljem vastava tegevuse teistest inimestest sõltumatult.

Alguses on korvis 9 õuna. Seejärel juhtuvad järgmised sündmused:

Aeg	Sündmus
0 sekundit	Alice vaatab korvi
4 sekundit	Bob vaatab korvi
7 sekundit	Carol vaatab korvi
8 sekundit	Dan vaatab korvi
10 sekundit	Erin vaatab korvi
11 sekundit	Frank vaatab korvi

Küsimus

Kui palju õunu lõpuks korvis on?

[Raadionupud]

A. 8 õuna

B. 9 õuna

C. 10 õuna

D. 11 õuna

E. 12 õuna

Vastus

Õige vastus on: B.

Vastuse selgitus

Allolev joonis näitab sündmusi, inimeste tegevusi ja õunte arvu muutumist ajateljel:

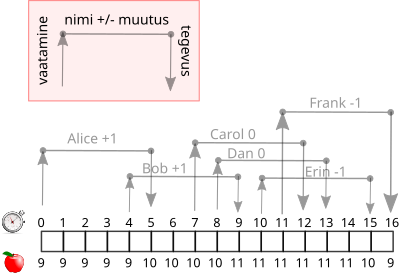
Ajatelje kohal olevad arvud näitavad sekundeid, ajatelje all on õunte arv korvis.

8. Telefoninumber

Ühes riigis on kasutusel 11-kohalised telefoninumbrid. Kuna inimesed teevad telefoninumbrite kirjutamisel ja meeldejätmisel sageli vigu, on selle riigi telefoninumbrites kasutusel järgmine süsteem:

number peab olema 7 esimese numbri (1. kuni 7.) summa viimane number.
number peab olema 4 esimese numbri (1. kuni 4.) summa viimane number.
number peab olema 1., 2., 5. ja 6. numbri summa viimane number.
number peab olema 1., 3., 5. ja 7. numbri summa viimane number.

Küsimus

Üks inimene selles riigis kirjutas üles telefoninumbri 12312316710.

Milline on õige telefoninumber, kui on teada, et inimene tegi vea täpselt ühes numbris?

(Sisesta täpselt 11 numbrit ilma tühikute või muude märkideta.)

[Tekstikast]

Vastus

Õige vastus on: 12315316710.

Vastuse selgitus

Vastuse leidmiseks vaatame kõigepealt telefoninumbri 12312316710 kontrollnumbreid:

number (6) ei sobi, sest 1+2+3+1+2+3+1 = 13.
number (7) sobib, sest 1+2+3+1 = 7.
number (1) ei sobi, sest 1+2+2+3 = 8.
number (0) ei sobi, sest 1+3+2+1 = 7.

Kui on teada, et kirjutaja tegi ainult ühe vea, ei saanud ta seda viga teha kontrollnumbrite osas, sest siin on mitu ebakõla. Järelikult peab viga olema seitsme esimese numbri hulgas.

9. number, mis on arvutatud nelja esimese numbri summana, sobib. Järelikult peavad need numbrid ka õiged olema.

Edasi näeme, et

number esineb 8., 10. ja 11. numbri arvutuses;
number esineb 8. ja 10. numbri arvutuses;
number esineb 8. ja 11. numbri arvutuses.

Kuna 8., 10. ja 11. number ükski ei sobi, peab viga olema 5. numbris, sest see on ainus, mis kõiki neid arvutusi mõjutab.

5. numbri õige väärtuse leidmiseks vaatame, milline see peaks olema, et 8. numbri arvutus õigesti välja tuleks. Peaks olema lihtne näha, et ainus sobiv väärtus on 5. Samuti on lihtne kontrollida, et selle muutuse järel tulevad õigesti välja ka 10. ja 11. numbri arvutused.

Seega peabki õige telefoninumber olema 12315316710.

9. Turniir

Täna peetakse iga-aastast kobraste turniiri. Turniiril osalevad 16 kobrast. Turniir koosneb neljast võistlusvoorust. Esimeses voorus võistlevad kõik 16 kobrast koos, aga edaspidi lähevad nende teed lahku. Iga vooru võitjad liiguvad järgmisse vooru (või oma kohale lõplikus pingereas) vasakpoolse noole suunas, kaotajad aga parempoolse noole suunas.

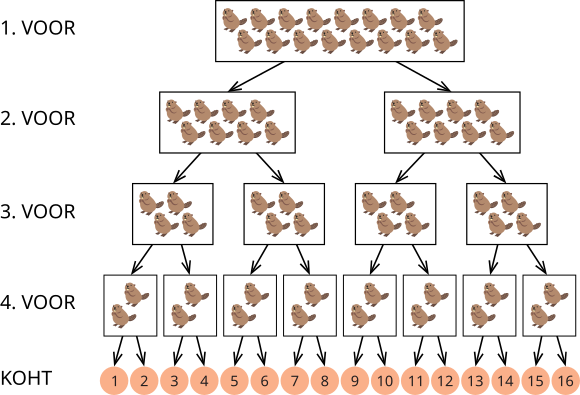
Näiteks kobras, kes võidab 1. ja 2. voorus, aga kaotab 3. ja 4. voorus, saavutab lõpuks 4. koha.

Küsimus

Noro on üks turniiril osalenutest. Millise koha ta võib saavutada, kui ta kaotab täpselt ühes voorus?

(Märgi kõik õiged vastused.)

[Märkeruudud 1..16]

Vastus

Õige vastus on: 2., 3., 5. või 9. koha.

Vastuse selgitus

Kuna turniiril on neli vooru ja Noro kaotab täpselt ühes voorus, on neli võimalikku stsenaariumi:

Ta kaotab 1. voorus ja võidab kõigis teistes voorudes. Siis liigub ta skeemis "paremale, vasakule, vasakule, vasakule" ja jõuab nii 9. kohale.
Ta kaotab 2. voorus ja võidab kõigis teistes voorudes. Siis liigub ta skeemis "vasakule, paremale, vasakule, vasakule" ja jõuab nii 5. kohale.
Ta kaotab 3. voorus ja võidab kõigis teistes voorudes. Siis liigub ta skeemis "vasakule, vasakule, paremale, vasakule" ja jõuab nii 3. kohale.
Ta kaotab 4. voorus ja võidab kõigis teistes voorudes. Siis liigub ta skeemis "vasakule, vasakule, vasakule, paremale" ja jõuab nii 2. kohale.

10. Praam

Suurel praamil on autotekil kuus rada. Äärmistele radadele A ja F mahub kummalegi 14 autot. Keskmistele radadele B, C, D ja E mahub igaühele 18 autot.

Autod sõidavad praamile järjekorranumbrite alusel ja meeskond paigutab nad tekile järgmiselt:

alguses paigutatakse autosid kordamööda radadele A ja F (esimene auto rajale A, teine auto rajale F, kolmas auto rajale A jne);
kui rajad A ja F saavad täis, hakatakse autosid paigutama kordamööda radadele B, C, D ja E (29. auto rajale B, 30. auto rajale C, 31. auto rajale D jne).

Küsimus

Millistele radadele paigutatakse järgmised autod?

[Vastavus]

A. Auto number 23

B. Auto number 47

C. Auto number 58

D. Auto number 77

Vastus

Õige vastus on: auto 23 — rajale A, auto 47 — rajale D, auto 58 — rajale C, auto 77 — rajale B.

Vastuse selgitus

Efektiivne viis selle ülesande lahendamiseks on panna tähele mustrit:

esimese 28 auto hulgas (radade A ja F täitumiseni) lähevad paaritute numbritega autod rajale A ja paarisnumbritega autod rajale F;
edasi lähevad rajale B need autod, mille järjekorranumbrid annavad 4-ga jagamisel jäägi 1; rajale C need, mis annavad jäägi 2; rajale D need, mis annavad jäägi 3 ja rajale E need, mille järjekorranumbrid jaguvad 4-ga.

Selle saab üles kirjutada ka formaalse tingimusena

kui number <= 28, siis
    kui number mod 2 == 1, siis
        rajale A
    muidu
        rajale F
muidu
    kui number mod 4 == 1, siis
        rajale B
    muidu kui number mod 4 == 2, siis
        rajale C
    muidu kui number mod 4 == 3, siis
        rajale D
    muidu
        rajale E

Siin 'X mod Y' tähendab jääki, mis tekib arvu X jagamisel arvuga Y.

11. Vihmutid

Amanda plaanib osta oma põllu kastmiseks uued vihmutid. Põld koosneb ruudukujulistest lappidest, millel kasvavad erinevad viljad, nagu näidatud alloleval kaardil.

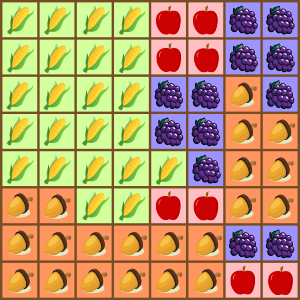
Aianduspoes müüakse vihmuteid 1×1, 2×2 ja 4×4 ruudu suuruste alade kastmiseks.

Kuna erinevaid vilju peab kastma erinevalt, ei tohi Amanda paigutada vihmuteid nii, et ühe vihmuti alla jääks mitut erinevat liiki viljadega ruute.

Samuti ei tohi ta vihmuteid paigutada nii, et mõnda ruutu kastaks mitu vihmutit või mõni vihmuti kastaks tema põllust väljapoole jäävat maad.

Küsimus

Milline on vähim arv vihmuteid, millega Amanda saab kogu oma põllu ära kasta?

[Raadionupud]

A. 19

B. 21

C. 23

D. 25

E. 27

Vastus

Õige vastus on: D.

Vastuse selgitus

Vihmutite arvu vähendamiseks tuleb kasutada võimalikult palju suuremaid vihmuteid.

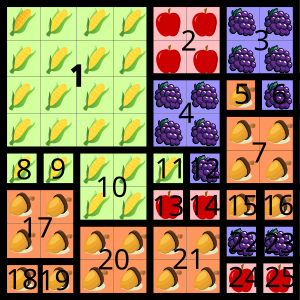
Amanda põllul on ainult üks 4×4 ruudu suurune ala, mis on kaetud ainult ühe viljaga (alloleval kaardil number 1).

Ülejäänud põllule mahub veel 8 vihmutit, mis kastavad 2×2 ruudu suuruseid alasid (alloleval kaardil numbrid 2, 3, 4, 7, 10, 17, 20, 21).

Ülejäänud 16 ruutu (8×8 [terve põld] - 1×(4×4) [üks 4×4 vihmuti] - 8×(2×2) [kaheksa 2×2 vihmutit]) tuleb katta 1×1 vihmutitega.

Kokku on seega vaja 1 + 8 + 16 = 25 vihmutit.

12. Piletiautomaat

Lõbustuspargis tuleb "Ameerika mägedele" piletit ostes sisestada müügiautomaati ostja sünnikuupäev ja pikkus, sest sinna lubatakse sõitma ainult külalisi, kes on vähemalt 13 aastat vanad ja vähemalt 120 cm pikad.

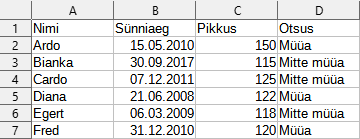
Piletiautomaadi sees on valem, mis kontrollib ostja sisestatud andmete vastavust tingimustele. Näiteks 4. veebruaril 2024 peaks valem tegema järgmised otsused:

Valemis võivad lisaks matemaatilistele tehetele (+, -, *, /) ja võrdlustele (>, <, >=, <=) olla kasutusel järgmised funktsioonid:

Funktsioon	Tähendus
`IF(X; Y; Z)`	Väärtus Y, kui tingimus X kehtib; väärtus Z, kui tingimus X ei kehti
`AND(X; Y)`	Tingimus, mis kehtib siis, kui kehtivad nii tingimus X kui ka tingimus Y
`OR(X; Y)`	Tingimus, mis kehtib siis, kui kehtib kas tingimus X või tingimus Y või tingimused X ja Y mõlemad
`NOW()`	Tänane kuupäev
`EDATE(X; Y)`	Kuupäev, mis saadakse, kui kuupäevale X liita Y kuud (kuupäevast X tulevikus, kui Y on positiivne; minevikus, kui negatiivne)

Küsimus

Milline valem peaks olema tabeli lahtris D2, et lahtrites B2 ja C2 andmete muutmisel tehtaks alati õige otsus?

[Raadionupud]

A. =IF(AND(EDATE(NOW();-13*12)>=B2;C2>=120);"Müüa";"Mitte müüa")

B. =IF(OR(EDATE(NOW();-13*12)>=B2;C2>=120);"Müüa";"Mitte müüa")

C. =IF(AND(EDATE(NOW();-13*12)<B2;C2>=120);"Müüa";"Mitte müüa")

D. =IF(OR(EDATE(NOW();-13*12)>=B2;C2<120);"Mitte müüa";"Müüa")

Vastus

Õige vastus on: A.

Vastuse selgitus

Variant A on õige, sest

EDATE(NOW();-13*12) leiab kuupäeva, mis on tänasest 13×12 kuud ehk 13 aastat tagasi;
EDATE(NOW();-13*12)>=B2 kontrollib, et ostja sünnikuupäev on sellega võrdne või sellest varasem;
C2>=120 kontrollib, et ostja pikkus on 120 cm või sellest suurem;
AND(EDATE(NOW();-13*12)>=B2;C2>=120) kontrollib, et kaks eelmist tingimust mõlemad kehtivad;
IF(AND(EDATE(NOW();-13*12)>=B2;C2>=120);"Müüa";"Mitte müüa") väljastab otsuse "Müüa" parajasti siis, kui mõlemad tingimused kehtivad.

Variant B ei ole õige, sest väljastab otsuse "Müüa", kui ostja rahuldab vähemalt üht kahest nõutud tingimusest; see tähendab, see valem lubab pileti müüa ka siis, kui ostja on küll piisavalt vana, aga liiga lühike, ja ka siis, kui ostja on küll piisavalt pikk, aga liiga noor.

Variant C ei ole õige, sest vanuse tingimus on valepidi; see valem lubab pileti müüa, kui ostja on vähemalt 120 cm pikk ja noorem kui 13 aastat.

Variant D väljastab otsuse "Mitte müüa", kui ostja on vähemalt 13 aastat vana või lühem kui 120 cm; see tähendab, et see valem lubab pileti müüa ainult siis, kui ostja on noorem kui 13 aastat ja vähemalt 120 cm pikk; tuleb välja, et see valem näeb küll väga erinev välja, aga arvutab täpselt sama tingimust kui variant C!

13. Teksti parandamine

Lihtsas tekstitöötlusprogrammis lisab täheklahvi vajutamine vastava tähe kursorist vasakule ja lisaks on võimalik kasutada mõningaid eriklahve, nagu näidatud allpool.

	Klahv "←" viib kursori ühe tähe võrra vasakule.
	Klahv "→" viib kursori ühe tähe võrra paremale.
	Klahv "bksp" kustutab kursorist vasakul oleva tähe.
	Klahv "del" kustutab kursorist paremal oleva tähe.
	Klahv "home" viib kursori rea algusse.
	Klahv "end" viib kursori rea lõppu.

Küsimus

Sidevigade tõttu muutus teksti "abcdefghijklm" edastamisel üks täht tärniks "*".

Milline on vähim klahvivajutuste arv, millega saab esialgse teksti taastada?

[Täisarv]

Vastus

Õige vastus on: 8.

Vastuse selgitus

Vea parandamiseks tuleb kõigepealt kursor tärni kõrvale liigutada, siis tärn ära kustutada ja siis õige täht asemele sisestada.

Võime tärni juurde liikuda "←"-klahviga. Sel juhul kulub 7 klahvivajutust, et kursor oleks tärnist paremal. Siis saame "bksp"-klahviga tärni ära kustutada ja "f"-klahviga õige tähe sisestada. Kokku kulub 9 klahvivajutust.

Teine variant on liikuda "home"-klahviga rea algusse ja siis "→"-klahviga tärni juurde. Sel juhul kulub 6 klahvivajutust, et kursor oleks tärnist vasakul. Siis saame "del"-klahviga tärni ära kustutada ja "f"-klahviga õige tähe sisestada. Kokku kulub 8 klahvivajutust.

Peaks olema ilmne, et kõik muud võimalikud lahendused teevad nende kahega võrreldes liigseid klahvivajutusi ja seega ei saa olla optimaalsed.

14. Pildi vähendamine

Koprad kasutavad piltide vähendamiseks järgmist meetodit:

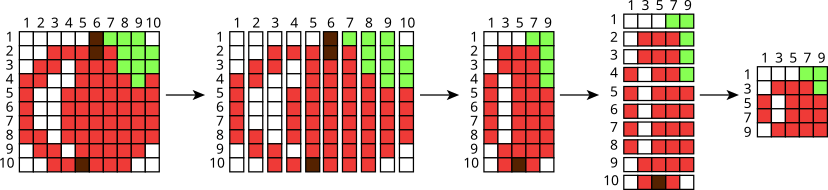
Esiteks lõikavad nad pildi vertikaalselt kümneks võrdse laiusega ribaks. Seejärel kleebivad nad paaritute numbritega ribad kokku uueks pildiks.

Siis lõikavad nad uue pildi horisontaalselt kümneks võrdse laiusega ribaks. Seejärel kleebivad nad paaritute numbritega ribad kokku lõplikult pildiks.

Küsimus

Milline on tulemus, kui allolevat pilti selle meetodiga vähendada?

[Raadionupud]

Vastus

Õige vastus on: B.

Vastuse selgitus

Meetodi rakendamine sammude kaupa:

15. Piltide jagamine

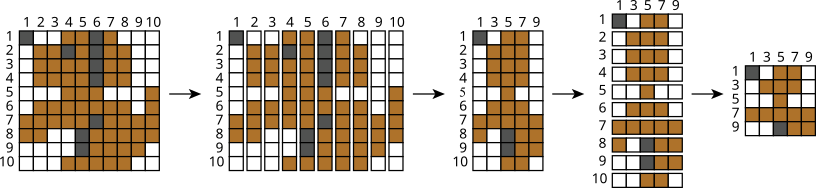
Sa tahad oma puhkusereisi pilte sõpradega jagada ja kaalud selleks erinevaid võimalusi ning nende mõju keskkonnale.

Üks viis keskkonnamõju mõõta on tekitatud CO2 koguse järgi:

ühe 3MB suuruse pildi oma seadmest pilve või pilvest oma seadmesse laadimine tekitab umbes 45g CO2;
ühe 3MB suuruse pildi pilves hoidmine tekitab umbes 60g CO2 aasta kohta;
ühe lühikese sõnumi saatmine tekitab umbes 1g CO2.

Sul on puhkuselt 10 pilti, igaüks umbes 3MB suurune, ja sa tahad neid jagada 5 sõbraga. Sul on selleks kolm võimalikku plaani:

Plaan 1: Saata pildid eraldi igale sõbrale SnapChati sõnumitena, mis ööpäeva pärast automaatselt ära kustuvad.

Plaan 2: Teha piltide jagamiseks nende 5 sõbraga SnapChati grupp ja jagada pilte grupisõnumitena, mis samuti ööpäeva pärast automaatselt ära kustuvad.

Plaan 3: Laadida pildid üles jagatud kettale pilves, saata kõigile sõpradele sõnumid jagatud ketta aadressiga ja aasta pärast kustutada pildid jagatud kettalt.

Küsimus

Milline allolevatest variantidest näitab õigesti eeltoodud plaanide CO2-heitmete hulkade suhteid?

[Raadionupud]

A. Plaan 1 < Plaan 3 < Plaan 2

B. Plaan 2 < Plaan 3 < Plaan 1

C. Plaan 2 < Plaan 1 < Plaan 3

D. Plaan 3 < Plaan 1 < Plaan 2

Vastus

Õige vastus on: B.

Vastuse selgitus

Vastuse leidmiseks on kõige lihtsam iga plaani tekitatud CO2 hulk välja arvutada:

Plaan 1: 10 pildi üles laadimine (10 × 45g) ja nende alla laadimine ühe sõbra poolt (10 × 45g) tekitavad kokku umbes 450g + 450g = 0,9kg CO2. Selle protsessi kordamine iga sõbra jaoks eraldi tekitab kokku 5 × 0,9kg = 4,5kg CO2. (Piltide ühe päeva jooksul SnapChati serveris hoidmisest tekkinud CO2 kogus on eelnevaga võrreldes tühine ja selle võib arvestamata jätta.)

Plaan 2: 10 pildi üles laadimine (10 × 45g) ja nende alla laadimine 5 sõbra poolt (5 × 10 × 45g) tekitavad kokku umbes 450g + 2250g = 2,7kg CO2. (Piltide ühe päeva jooksul SnapChati serveris hoidmisest tekkinud CO2 kogus on eelnevaga võrreldes tühine ja selle võib arvestamata jätta.)

Plaan 3: 10 pildi üles laadimine (10 × 45g), nende hoidmine aasta jooksul (10 × 60g) ja nende alla laadimine 5 sõbra poolt (5 × 10 × 45g) tekitavad kokku umbes 450g + 600g + 2250g = 3,3kg CO2. (5 lühikese sõnumi saatmisega tekkinud CO2 kogus on eelnevaga võrreldes tühine ja selle võib arvestamata jätta.)

Flag icons by GoSquared.