

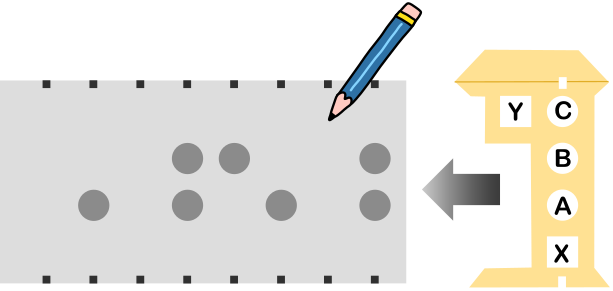
На рисунке показаны шаблон с пятью отверстиями (A, B, C, X, Y) и карандаш, которые следует использовать следующим образом:
Например, результат работы с листом бумаги, показанным на вышеприведённом рисунке, выглядит следующим образом:

Каков будет результат, если таким же образом будут работать с нижеприведённым листом бумаги?

[Raadionupud]
A. 
B. 
C. 
D. 
Правильный ответ: C.
Чтобы найти правильный ответ, проще всего описанный в задании алгоритм проработать мысленно или на бумаге.

|
В киберсаду цветы растут в квадратных ячейках. У каждой ячейки по 8 соседей. Например, на приведённом |

|
Киберсад развивается по следующим правилам:
Рассмотрим пример:
| 1ый день | 2ой день |
|---|---|
 |
 |
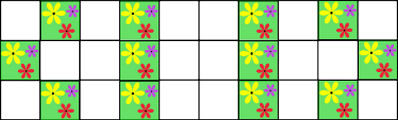
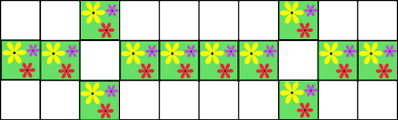
Сколько цветных ячеек будет в нижеприведённом саду на следующий день?
(За пределами сада нет цветных ячеек.)
[Täisarv]
Правильный ответ: 12.
Применяя ко всем ячейкам сада вышеописанные четыре правила, получим: //kõigile ruutudele -> lahtritele?//

В разных странах на номерных знаках машин используются разные наборы букв и цифр. В основном в номерных знаках используются заглавные буквы английского алфавита (их 26) и цифры (их, конечно же, 10).
В какой из нижеперечисленных стран можно выдать наибольшее количество различных номерных знаков?
При ответе исходи из того, что все номерные знаки этой страны имеют тот же набор букв и цифр, что и в приведённых в вариантах ответов примерах. Это значит, что, если в каком-то месте в примере стоит буква, то во всех номерных знаках этой страны на этом месте может быть любая буква (но не цифра), и то же самое касается цифр. Следует учитывать только приведённые на белом фоне заглавные буквы и цифры, а не те, что указаны в кодах стран или на гербах.
[Raadionupud]
A.  (Финляндия)
(Финляндия)
B.  (Словакия)
(Словакия)
C.  (Румыния)
(Румыния)
D.  (Швейцария)
(Швейцария)
E.  (Украина)
(Украина)
Правильный ответ: E.
Чтобы решить это задание, нам нужно найти количество возможных (различных) номерных знаком для каждой страны. Для этого, в свою очередь, достаточно посчитать, сколько букв и сколько цифр в номерных знаках этой страны. Поскольку существует 26 способов выбора каждой буквы и 10 способов выбора каждой цифры, то мы получим следующие результаты:
A. 3 буквы и 3 цифры: 263 × 103;
B. 4 буквы и 3 цифры: 264 × 103;
C. 5 букв и 2 цифры: 265 × 102;
D. 2 буквы и 6 цифр: 262 × 106;
E. 4 буквы и 4 цифры: 264 × 104.
Вычисление этих чисел довольно хлопотное занятие, но это и не обязательно. Во многих случаях достаточно посмотреть на частное двух чисел и сократить аналогичные члены:
B / A = (264 × 103) / (263 × 103) = 26 > 1 (следовательно, B > A);
C / B = 26/10 > 1 (следовательно, C > B);
E / C = 102/26 = 100 / 26 > 1 (следовательно, E > C);
E / D = 262/102 = (26/10)2 > 1 (следовательно, E > D).

|
Производящая цифровые атласы фирма хочет сделать фотографии всех Служебному автомобилю требуется один час, чтобы сфотографировать |

|

По скольким различным маршрутам может проехать автомобиль, выезжающий из деревни R, чтобы завершить работу за семь часов?
[Raadionupud]
A. 6
B. 8
C. 10
D. 12
Правильный ответ: D.
Чтобы сфотографировать все дороги за семь часов, машина должна проехать каждую дорогу ровно один раз.
Это значит, что варианты есть только в случае деревень R, P и S. Поскольку через деревни T и Q всегда нужно проезжать насквозь, они не влияют на количество возможных маршрутов, и их можно не учитывать. Следовательно, мы можем составить упрощённую схему дорожной сети:
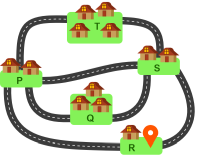
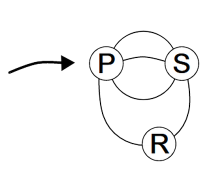
Если машина стартует из деревни R, она также должна и финишировать в деревне R.
Предположим, что машина выезжает из деревни R в правую сторону и доезжает до деревни S. Здесь у неё появляется выбор в каком порядке наносить на карту имеющиеся между деревнями S и P дороги, но дорогу, ведущую из деревни P в деревню R, необходимо нанести на карту последней.
Чтобы первый раз проехать из деревни S в деревню P, мы можем выбрать одну из трёх дорог (нижнюю, среднюю или верхнюю). Для возвращения из деревни P в деревню S у нас есть на выбор только две дороги, потому что машина потеряла бы время, возвращаясь той же дорогой, которой приехала. При движении из деревни S в деревню P во второй раз выбора уже нет - всегда приходиться выбирать ту дорогу, которая после двух предыдущих поездок всё ещё отсутствует на карте. Таким образом, при движении из деревни S в деревню P всего имеется 3 x 2 x 1 = 6 возможностей для картографирования всех трёх дорог.
Итак, выезжая вправо от деревни R, есть 6 возможностей нанести на карту все дороги за оптимальное время. Рассуждая аналогично, придём к выводу, что при движении влево от деревни R у нас также есть 6 возможностей.
Следовательно, всего имеется 12 возможностей.

В Бобруйске построили девять новых домов. Староста деревни решил, что три новых дома должны быть покрашены в жёлтый цвет, три в красный и три в синий. Он также решил, что никакие два дома, соединённые между собой дорогой, не должны быть одного и того же цвета.
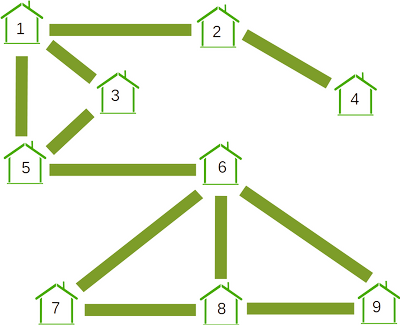
Какие два дома обязательно будут покрашены в один и тот же цвет?
[Märkeruudud]
A. Дом под номером 1
B. Дом под номером 2
C. Дом под номером 3
D. Дом под номером 4
E. Дом под номером 5
F. Дом под номером 6
G. Дом под номером 7
H. Дом под номером 8
I. Дом под номером 9
Правильный ответ: G и I (дома под номерами 7 и 9).
Дома под номерами 7 и 9 обязательно должны быть одного и того же цвета: дома под номерами 6 и 8 соединены между собой и поэтому должны быть разного цвета; дом под номером 7 соединён с ними обоими и поэтому должен быть третьего цвета; то же самое относится и к дому под номером 9.
Но как же убедиться в том, что это единственные дома, которые обязательно должны быть одного и того же цвета? Давайте рассмотрим следующие три возможности покраски, каждая из которых соответствует требованиям старосты деревни:
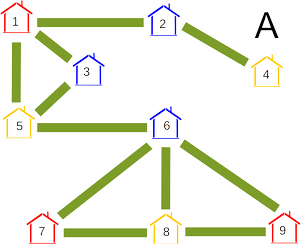
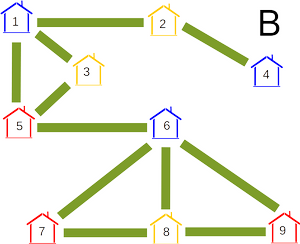
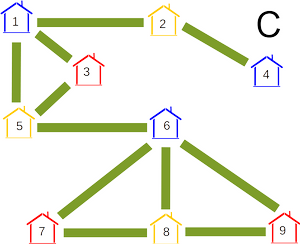
Сначала рассмотрим дома под номерами 1, 2, 3, 4, 5. В варианте А пары {2, 3} и {4, 5} имеют один и тот же цвет. Но в варианте C обе эти пары имеют разные цвета.
Теперь рассмотрим дома под номерами 6, 7, 8, 9. В этой группе во всех трёх вариантах все пары, кроме {7, 9}, разного цвета.
Наконец, рассмотрим пары, в которых один дом будет из группы 1–5, а другой — из группы 6–9. Здесь можем заметить, что в вариантах А и B цвета домов под номерами 6–9 одинаковы, а цвета домов под номерами 1–5 различаются. Таким образом, каждая такая пара имеет разный цвет хотя бы в одном из этих двух вариантов.
Следовательно, нет больше пар, кроме домов под номерами 7 и 9, которые при всех возможных способах покраски были бы одного и того же цвета.



Дигитальные часы используют светодиодные (LED) индикаторы для отображения цифр. Каждый индикатор имеет семь сегментов, которые можно включать и выключать. На нижеприведённом рисунке показано, как с помощью таких индикаторов отображаются цифры от 0 до 9.

Сегменты индикатора изнашиваются, когда они светятся. Тот сегмент, который больше всего горит в течение недели, изнашивается быстрее всего и его необходимо заменить в первую очередь.
Какой из 28 сегментов необходимо заменить в первую очередь?
(В качестве ответа запиши одну цифру и одну букву, как показано на нижеприведённом рисунке.)
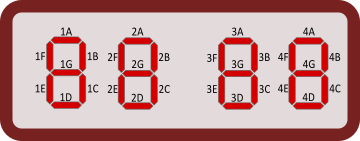
[Tekstikast]
Правильный ответ: 1B.
Часы работают и показывают время 24 часа в сутки. В течение недели это происходит неизменно, изо дня в день. Это значит, что для решения этого задания, вместо недели мы можем сосредоточиться на том, что происходит в течение одних суток.
В течение суток часы показывают время с 00:00 до 23:59. Из приведённого примера 04:01 видно, что однозначные числа отображаются как двузначные, но путём добавления нуля в начало числа.

|
В местах, где светятся десятки часов, могут быть только цифры 0, 1 и 2. Во всех трёх этих цифрах используется сегмент B. Это значит, что сегмент B индикатора десятков часов светится круглосуточно, никогда не выключаясь. Это также единственный сегмент, который светится круглосуточно. Чтобы убедиться в этом, рассмотрим цифры 1, 2 и 5. В цифре 1 светятся только сегменты В и С. А вот в цифре 2 сегмент С не светится, но в цифре 5 не светится сегмент В. Поскольку единицы часов, а также десятки и единицы минут используют цифры 1, 2 и 5, то во всех этих индикаторах каждый сегмент выключен по крайней мере какую-то часть суток. |

|
Группа людей пытается добиться того, чтобы в корзине было ровно 10 яблок. |

|
Когда кто-то из них заглядывает в корзину, он действует согласно тому, что видит в корзине:
| Содержимое корзины | Действие |
|---|---|
| Меньше 10 яблок | Добавляет в корзину одно яблоко |
| Больше 10 яблок | Убирает из корзины одно яблоко |
| Ровно 10 яблок | Ничего не делает |
Подсчёт яблок происходит мгновенно, без затрачивания времени. А вот добавление или удаление яблока из корзины занимает 5 секунд.
Люди не общаются друг с другом. Каждый заглядывает в корзину и через 5 секунд независимо от других людей выполняют соответствующее действие.
Сначала в корзине было 9 яблок. Затем произошли следующие события:
| Время | Событие |
|---|---|
| 0 секунд | Алла заглянула в корзину |
| 4 секунды | Боря заглянул в корзину |
| 7 секунд | Вася заглянул в корзину |
| 8 секунд | Галя заглянула в корзину |
| 10 секунд | Диана заглянула в корзину |
| 11 секунд | Егор заглянул в корзину |
Сколько яблок в итоге оказалось в корзине?
[Raadionupud]
A. 8 яблок
B. 9 яблок
C. 10 яблок
D. 11 яблок
E. 12 яблок
Правильный ответ: B.
На нижеприведённом рисунке с помощью временной шкалы показаны события, действия людей и изменения в количестве яблок:
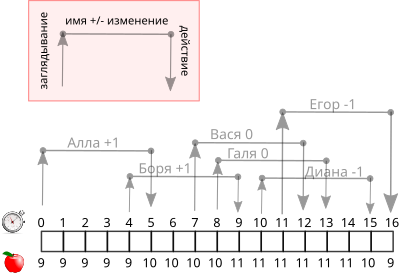
Цифры над временной шкалой показывают секунды, под временной шкалой — количество яблок в корзине.

В одной стране используются 11-значные телефонные номера. Поскольку при написании и запоминании номеров телефонов люди часто допускают ошибки, то в телефонных номерах этой страны используется следующая система:
|
8ая цифра является последней цифрой суммы первых 7 цифр (с 1ой по 7ую). 9ая цифра является последней цифрой суммы первых 4 цифр (с 1ой по 4ую). 10ая цифра является последней цифрой суммы 1ой, 2ой, 5ой и 6ой цифр. 11ая цифра является последней цифрой суммы 1ой, 3ей, 5ой и 7ой цифр. |

|
Человек из этой страны записал номер телефона 12312316710.
Какой правильный номер телефона, если известно, что человек ошибся ровно в одной цифре?
(Запиши только 11 цифр без пробелов и других символов.)
[Tekstikast]
Правильный ответ: 12315316710.
Чтобы найти ответ, сначала посмотрим на контрольные цифры телефона 12312316710:
8ая цифра (6) не подходит, потому что 1+2+3+1+2+3+1 = 13. 9ая цифра (7) подходит, потому что 1+2+3+1 = 7. 10ая цифра (1) не подходит, потому что 1+2+2+3 = 8. 11ая цифра (0) не подходит, потому что 1+3+2+1 = 7.
Если известно, что человек допустил только одну ошибку, то он не мог допустить этой ошибки в контрольных цифрах, потому что здесь имеется несколько несоответствий. Значит, ошибка должна быть в первых семи цифрах.
9ая цифра, которая находится путём сложения первых четырёх цифр (используется последняя цифра суммы), подходит. Значит, эти цифры также должны быть верными.
Далее мы можем заметить, что
5ая цифра появляется в расчётах 8ой, 10ой и 11ой цифр; 6ая цифра появляется в расчётах 8ой и 10ой цифр; 7ая цифра появляется в расчётах 8ой и 11ой цифр.
Поскольку ни одна из цифр, записанная на 8ой, 10ой и 11ой позиции не подходит, то ошибка должна быть в 5ой цифре, потому что эта цифра единственная, которая влияет на все эти вычисления.
Чтобы найти правильное значение 5ой цифры, давайте посмотрим, каким оно должно быть, чтобы вычисление 8ой цифры было правильным. Должно быть заметно, что единственным допустимым значением является 5. Также легко проверить, что после этого изменения выполняются правильно и вычисления для 10ой и 11ой цифр.
Таким образом, правильный номер телефона должен быть 12315316710.

Сегодня состоится ежегодный турнир среди бобров. В турнире примут участие 16 бобров. Турнир состоит из четырёх туров. В первом туре все 16 бобров соревнуются вместе, но далее их пути расходятся. Победители каждого тура проходят в следующий тур (или на своё место в итоговой таблице), как показывает направление левой стрелки, а проигравшие двигаются в направлении правой стрелки.
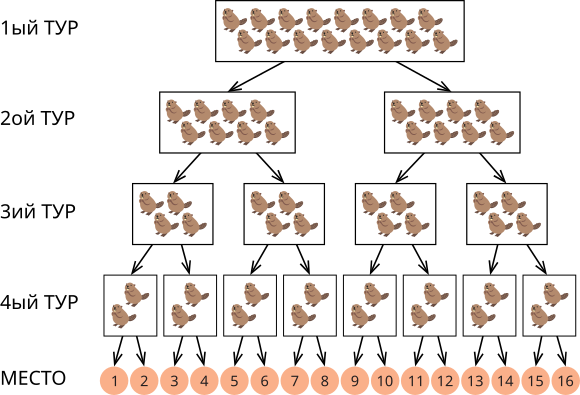
Например, бобр, который выиграет в 1ом и 2ом турах, но проиграет в 3ем и 4ом турах, в итоге получит 4ое место.
Норо один из участников турнира. Какое место он может получить, если проиграет только один тур?
(Отметь все правильные ответы.)
[Märkeruudud 1..16]
Правильный ответ: 2ое, 3ье, 5ое или 9ое место.
Поскольку турнир состоит из четырёх туров, и Норо проиграет только один тур, то имеется четыре возможных сценария:
Он проиграет в 1ом туре и выиграет в трёх других турах. Тогда, следуя схеме, он будет двигаться "направо, налево, налево, налево" и получит 9ое место.
Он проиграет во 2ом туре и выиграет в трёх других турах. Тогда, следуя схеме, он будет двигаться "налево, направо, налево, налево" и получит 5ое место.
Он проиграет в 3ем туре и выиграет в трёх других турах. Тогда, следуя схеме, он будет двигаться "налево, налево, направо, налево" и получит 3ье место.
Он проиграет в 4ом туре и выиграет в трёх других турах. Тогда, следуя схеме, он будет двигаться "налево, налево, налево, направо" и получит 2ое место.

Большой паром на автомобильной палубе имеет шесть дорожек для размещения машин. Каждая из внешних дорожек A и F вмещает по 14 машин. Каждая из средних дорожек B, C, D и E вмещает по 18 машин.

Машины заезжают на паром по порядковым номерам, и экипаж размещает их на палубе следующим образом:
На каких дорожках размещаются следующие машины?
[Vastavus]
A. Машина под номером 23
B. Машина под номером 47
C. Машина под номером 58
D. Машина под номером 77
Правильный ответ: машина под номером 23 — на дорожку A, машина под номером 47 — на дорожку D, машина под номером 58 — на дорожку C, машина под номером 77 — на дорожку B.
Эффективный способ решить это задание — это заметить закономерность:
среди первых 28 машин (до заполнения дорожек А и F) на дорожке А размещаются машины с нечётными порядковыми номерами, а на дорожке F — машины с чётными порядковыми номерами;
далее на дорожке B размещаются те машины, у которых порядковые номера при делении на 4 дают остаток 1; на дорожке C те, которые дают остаток 2; на дорожке D те, которые дают остаток 3, и на дорожке E те, чьи порядковые номера делятся на 4.
Это также можно записать как формальное условие
если число <= 28, то
если число mod 2 == 1, то
на дорожку A
иначе
на дорожку F
иначе
если число mod 4 == 1, то
на дорожку B
иначе если число mod 4 == 2, то
на дорожку C
иначе если число mod 4 == 3, то
на дорожку D
иначе
на дорожку EЗдесь 'X mod Y' означает остаток, который получается при делении числа X на число Y.

Аманда планирует купить новые разбрызгиватели воды для полива своего поля. Поле состоит из квадратных участков, на которых растут разные плоды, как показано на нижеприведённой карте.
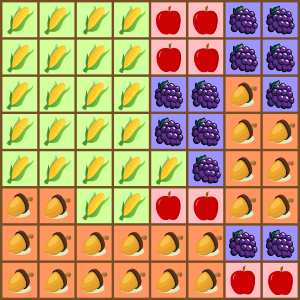
В садовом магазине продаются разбрызгиватели воды для полива участков размером 1х1, 2х2 и 4х4 квадрата.
Поскольку разные плоды нужно поливать по-разному, Аманда не может разместить разбрызгиватели воды таким образом, чтобы под одним разбрызгивателем оказались участки с несколькими разными видами плодов.
Она также не может разместить разбрызгиватели воды таким образом, чтобы какой-нибудь участок поливался несколькими разбрызгивателями или чтобы какой-нибудь разбрызгиватель поливал участки земли за пределами её поля.
Какое наименьшее количество разбрызгивателей воды понадобится Аманде, чтобы полить всё поле?
[Raadionupud]
A. 19
B. 21
C. 23
D. 25
E. 27
Правильный ответ: D.
Для уменьшения количества разбрызгивателей воды, следует использовать как можно больше разбрызгивателей большего размера.
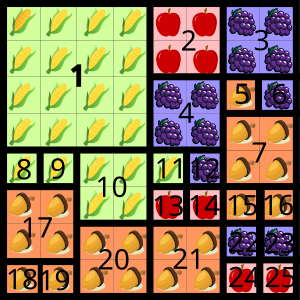
На поле Аманды есть только один участок размером 4×4, на котором выращивается только один плод (под номером 1 на нижеприведённой карте).
На оставшемся поле можно разместить еще 8 разбрызгивателей воды, которые поливают участки размером 2×2 квадрата (под номерами 2, 3, 4, 7, 10, 17, 20, 21 на нижеприведённой карте).
Оставшиеся 16 квадратов (8×8 [всё поле] - 1×(4×4) [один участок 4×4] - 8×(2×2) [восемь участков 2×2]) должны поливать разбрызгиватели, каждый из которых покроет участок размером 1×1.
Следовательно, Аманде понадобится всего 1 + 8 + 16 = 25 разбрызгивателей воды.

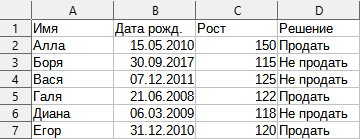
В парке аттракционов при покупке билета на «Американские горки» в автомате необходимо ввести дату рождения и рост покупателя, потому что на аттракцион допускаются только гости не моложе 13 лет и ростом не менее 120 см.
Внутри автомата по продаже билетов используется формула, которая проверяет введённые данные на соответствие условиям. Например, 4 февраля 2024 г. формула должна была бы вернуть следующие решения:
В формуле помимо математических действий (+, -, *, /) и сравнений (>, <, >=, <=) могут использоваться следующие функции:
| Функция | Значение |
|---|---|
IF(X; Y; Z) |
Выводит значение Y, если условие X выполняется; значение Z, если условие X не выполняется |
AND(X; Y) |
Условие, которое выполняется тогда, когда выполняется и условие X, и условие Y |
OR(X; Y) |
Условие, которое выполняется тогда, когда выполняется либо условие X, либо условие Y, либо оба условия X и Y |
NOW() |
Сегодняшняя дата |
EDATE(X; Y) |
Дата, полученная путём прибавления Y месяцев к дате X (от даты X в будущее, если Y положительно; в прошлое, если отрицательно). |
Какая формула должна быть в ячейке D2 таблицы, чтобы при изменении данных в ячейках B2 и C2 всегда принималось правильное решение?
[Raadionupud]
A. =IF(AND(EDATE(NOW();-13*12)>=B2;C2>=120);"Продать";"Не продать")
B. =IF(OR(EDATE(NOW();-13*12)>=B2;C2>=120);"Продать";"Не продать")
C. =IF(AND(EDATE(NOW();-13*12)<B2;C2>=120);"Продать";"Не продать")
D. =IF(OR(EDATE(NOW();-13*12)>=B2;C2<120);"Не продать";"Продать")
Правильный ответ: A.
Вариант A верный, потому что
EDATE(NOW();-13*12) находит дату, которая была в прошлом 13×12 месяцев или 13 лет назад;EDATE(NOW();-13*12)>=B2 проверяет, чтобы дата рождения покупателя была равна или раньше, чем найденная дата;C2>=120 проверяет, чтобы рост покупателя был 120 см или больше;AND(EDATE(NOW();-13*12)>=B2;C2>=120) проверяет, чтобы два предыдущих условия оба выполнялись;IF(AND(EDATE(NOW();-13*12)>=B2;C2>=120);"Продать";"Не продать") выводит решение "Продать" тогда и только тогда, когда оба условия выполняются.Вариант B неверен, потому что выводит решение «Продать», если покупатель выполняет хотя бы одно из двух требований. Это значит, что эта формула позволяет продать билет, даже если покупатель достаточно взрослый, но слишком низкого роста, а также в случае, если покупатель достаточно высокий, но слишком молод.
Вариант C неверен, потому что условие возраста записано наоборот. Эта формула позволяет продать билет, если рост покупателя не менее 120 см, и он моложе 13 лет.
Вариант D выводит решение «Не продать», если покупателю по меньшей мере 13 лет или он ростом ниже 120 см. Это значит, что данная формула позволяет продать билет только в том случае, если покупатель моложе 13 лет и ростом не менее 120 см. Оказывается, эта формула выглядит совсем по-другому, но рассчитывает точно такое же условие, что и вариант С!

В простом текстовом редакторе при нажатии на клавишу с буквой соответствующая буква добавляется слева от курсора, а также можно использовать некоторые специальные клавиши, которые показаны ниже.

|
Клавиша "←" перемещает курсор на одну букву влево. |

|
Клавиша "→" перемещает курсор на одну букву вправо. |

|
Клавиша "bksp" удаляет букву, которая находится слева от курсора. |

|
Клавиша "del" удаляет букву, которая находится справа от курсора. |

|
Клавиша "home" перемещает курсор в начало строки. |

|
Клавиша "end" перемещает курсор в конец строки. |
Из-за ошибок в связи при передаче текста "abcdefghijklm" одна буква была заменена на звёздочку "*".

Каково наименьшее количество нажатий на клавиши позволит восстановить первоначальный текст?
[Täisarv]
Правильный ответ: 8.
Чтобы исправить ошибку, нам сначала потребуется переместить курсор к звёздочке, затем удалить звёздочку, а потом уже ввести правильную букву. К звёздочке мы можем переместиться с помощью клавиши "←". Нажав на неё 7 раз, курсор окажется справа от буквы. Далее, нажав на клавишу "bksp", мы удалим звёздочку, а, нажав на клавишу "f", мы введём правильную букву. Итого нам понадобится 9 нажатий на клавиши.
Второй вариант — это с помощью клавиши "home" переместиться в начало строки, а далее, нажав на клавишу "→", переместиться к звёздочке. Нажав на клавишу "→" 6 раз, курсор окажется слева от звёздочки. Далее, нажав на клавишу "del", мы удалим звёздочку, а, нажав на клавишу "f", мы введём правильную букву. Итого нам понадобится 8 нажатий на клавиши.
Должно быть понятным, что все другие возможные решения потребуют лишних (по сравнению с этими двумя решениями) нажатий на клавиши, и поэтому не являются оптимальными.

Бобры используют следующий метод для сжатия картинок:
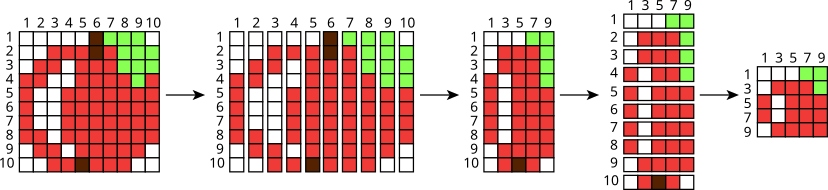
Первым делом они разрезают картинку вертикально на десять полосок одинаковой ширины. Далее они склеивают полоски с нечётными номерами в новую картинку.
После этого они разрезают уже новую картинку горизонтально на десять полосок одинаковой ширины. Затем они склеивают полоски с нечётными номерами и получают итоговую картинку.
Каков будет результат, если нижеприведённую картинку сжать с помощью этого метода?
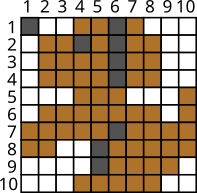
[Raadionupud]
A. 
B. 
C. 
D. 
Правильный ответ: B.
Пошаговое применение метода выглядит следующим образом:
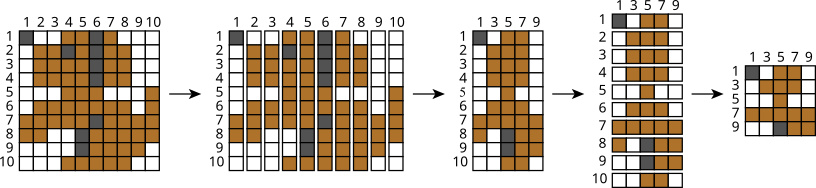

|
Тебе хочется поделиться с друзьями своими фотографиями с отпуска. Ты обдумываешь разные варианты как это сделать и хочешь учесть влияние каждого варианта на окружающую среду. Один из способов измерения влияния на окружающую среду основывается на количестве выбросов CO2:
У тебя 10 фотографий с отпуска, каждая размером примерно по 3МБ, и тебе хочется поделиться ими с 5 друзьями. Чтобы это сделать, у тебя есть три возможных плана: План 1: Отправить фотографии отдельно каждому другу, используя сообщения SnapChat'а. Через сутки сообщения автоматически удалятся. План 2: Создать группу в SnapChat'е, чтобы поделиться фотографиями с 5 друзьями. Далее отправить фотографии с помощью групповых сообщений, которые также через сутки автоматически удалятся. План 3: Загрузить фотографии на общий диск в облаке, отправить всем друзьям сообщения с адресом общего диска и через год удалить фотографии с общего диска. |

|
Какой из нижеприведённых вариантов верно показывает отношения между описанными планами по количеству выбросов CO2?
[Raadionupud]
A. План 1 < План 3 < План 2
B. План 2 < План 3 < План 1
C. План 2 < План 1 < План 3
D. План 3 < План 1 < План 2
Правильный ответ: B.
Чтобы найти ответ, проще всего посчитать количество выбросов CO2 для каждого плана:
План 1: загрузка 10 фотографий (10 × 45гр) и их скачивание одним другом (10 × 45g) в итоге приведут к примерно 450гр + 450гр = 0,9кг CO2. Повторение этого процесса каждым из друзей по отдельности приведёт в итоге к 5 × 0,9кг = 4,5кг CO2. (Количество выбросов CO2, вызванное хранением фотографий в течение одних суток на сервере SnapChat'а, можно считать ничтожно малым по сравнению с предыдущими вычислениями, и это значение можно не учитывать.)
План 2: загрузка 10 фотографий (10 × 45гр) и их скачивание 5 друзьями (5 × 10 × 45гр) приведёт к примерно 450гр + 2250гр = 2,7гр CO2. (Количество выбросов CO2, вызванное хранением фотографий в течение одних суток на сервере SnapChat'а, можно считать ничтожно малым по сравнению с предыдущими вычислениями, и это значение можно не учитывать.)
План 3: загрузка 10 фотографий (10 × 45гр), их хранение в течение года (10 × 60гр) и их скачивание 5 друзьями (5 × 10 × 45гр) приведут к примерно 450гр + 600гр + 2250гр = 3,3гр CO2. (Количество выбросов CO2, вызванное отправкой 5 коротких сообщений, можно считать ничтожно малым по сравнению с предыдущими вычислениями, и это значение можно не учитывать.)
Copyright © 2023 Bebras – International Challenge on Informatics and Computational Thinking.
Licensed under Creative Commons Attribution-ShareAlike 4.0 International License.
Flag icons by GoSquared.