1. Šabloon

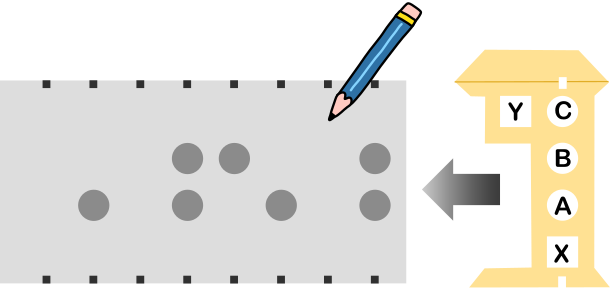
Joonisel näidatud viie auguga (A, B, C, X, Y) šablooni ja pliiatsit kasutatakse järgmiselt:

Liiguta šabloon paberi parempoolsema veeru kohale.
Kui šablooni aukudest A, B ja C paistab paaritu arv halle ringe, värvi šablooni auku X ruut.
Kui šablooni aukudest A, B ja C paistab kaks või rohkem halli ringi, värvi šablooni auku Y ruut.
Liiguta šabloon ühe veeru võrra vasakule. (Pane tähele, et kui šabloon edasi liigub, paistab varem auku Y värvitud ruut läbi augu C ringina.)
Korda eelnevaid samme, kuni šabloon jõuab paberi vasakpoolseima veeru kohale.

Näiteks ülaloleval joonisel kujutatud paberi töötlemise tulemus on selline:

Küsimus

Milline on tulemus, kui samamoodi töödeldakse allolevat paberit?

[Raadionupud]

Vastus

Õige vastus on: C.

Vastuse selgitus

Õige vastuse leidmiseks on kõige lihtsam ülesande tekstis kirjeldatud algoritm läbi teha, kas mõttes või paberil.

2. Jalutuskäik

Kobras Peeter armastab metsas jalutada. Ta alustab alati oma kodust, mis on kaardi vasakus alumises nurgas, ja lõpetab kaardi paremas ülemises nurgas, kus on ilus jõekäär.

Jalutades liigub ta alati kaardil paremale või üles ja väldib mesilasi .

Peeter armastab ka vaheldust ja ei taha jalutada kaks korda täpselt sama teed. Ta sai kiiresti aru, et alloleval joonisel näidatud metsas on tal kolm erinevat võimalikku teed läbi metsa:

Küsimus

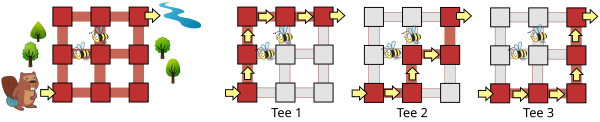
Peeter käib sageli külas oma sõbral Jaanil, kes elab natuke suuremas metsas.

Mitu erinevat teed on Peetril jalutamiseks allolevas suuremas metsas, kui ta endiselt jalutab kaardi vasakust alumisest nurgas paremale ülemisse, liikudes ainult paremale või üles ja vältides mesilasi?

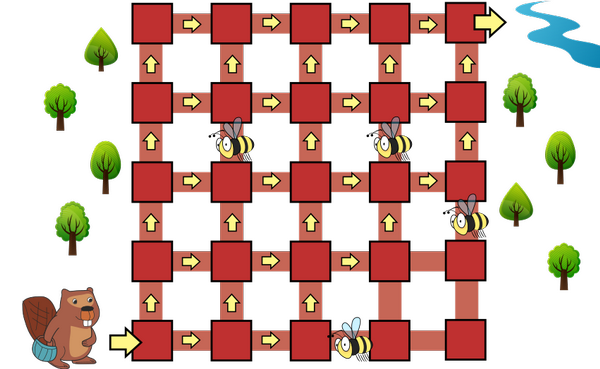
[Täisarv]

Vastus

Õige vastus on: 32.

Vastuse selgitus

Vastust võiks proovida leida kõiki variante üles kirjutades, aga see oleks ajakulukas ja ka veaohtlik. Samas on ka strateegia, mis võimaldab isegi üsna suuri kaarte efektiivselt analüüsida.

Vaatame alguses näitena jalutamist väiksemas metsas. Võime selle esitada 3×3 tabelina, kus iga lahter on üks radade ristumiskoht ja punased jooned näitavad mesilaste asukohti, kust läbi minna ei tohi. Seega on ülesanne loendada selles tabelis ruudust (1,1) ruutu (3,3) liikumise võimalused.

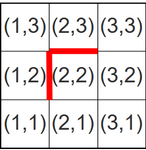
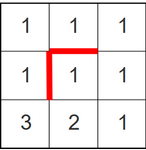
Sellises esituses saame tabeli igasse lahtrisse kirjutada sellest lahtrist algavate ja paremal ülemises nurgas lõppevate teede arvu. Alustame sellest, et kirjutame lahtrisse (3,3) arvu 1, sest seal pole muud võimalust, kui astuda kaardilt välja jõe äärde. Samuti kirjutame arvud 1 kõigisse teistesse rea 3 ja veeru 3 lahtritesse, sest ka sealt on ainult üks võimalik tee lõpuni.

Kui me mesilasi ei arvesta, peaks ülejäänud lahtrite vahel kehtima seos teid(x,y)=teid(x+1,y)+teid(x,y+1), sest lahtrist (x,y) võime liikuda lahtrisse (x+1,y), kust lõpuni jalutamiseks on teid(x+1,y) võimalust, või lahtrisse (x,y+1), kust lõpuni jalutamiseks on teid(x,y+1) võimalust. Kui mesilased mõnest lahtrist paremale või üles liikumist takistavad, siis selle lahtri sisu arvutamisel jätame vastava liidetava välja. Nii saamegi tabeli ülalt alla ja paremalt vasakule täita ja lugeda lahtrist (1,1) otsitava vastuse.

Tehes samad sammud läbi suurema metsa kaardile vastavas tabelis, saame tulemuseks:

3. Autonumbrid

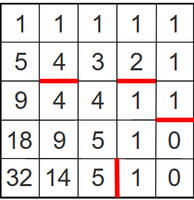
Erinevates riikides on autonumbritel kasutusel erinevad tähtede ja numbrite mustrid. Üldiselt kasutatakse autonumbrites inglise tähestiku suurtähti (mida on 26) ja numbreid (mida on muidugi 10).

Küsimus

Millises alltoodud riikidest on võimalik välja anda kõige rohkem erinevaid autonumbreid?

Vastamisel eeldada, et kõik autonumbrid selles riigis on sama tähtede/numbrite mustriga kui vastusevariandis toodud näide. Täpsemalt, kui näites on mingis kohas täht, siis võib selle riigi autonumbrites selles kohas olla ükskõik milline täht (aga mitte number), ja samamoodi ka numbrite korral. Arvestada ainult valgel taustal olevaid suuri tähti ja numbreid, mitte riigikoodides või vappidel olevaid.

[Raadionupud]

A. (Soome)

B. (Slovakkia)

C. (Rumeenia)

D. (Šveits)

E. (Ukraina)

Vastus

Õige vastus on: E.

Vastuse selgitus

Vastamiseks peame leidma igas riigis võimalike erinevate autonumbrite arvud. Selleks omakorda piisab, kui loeme kokku mitu tähte ja mitu numbrit selle riigi autonumbrites on. Kuna iga tähe valimiseks on 26 ja iga numbri valimiseks 10 võimalust, siis saame järgmised tulemused:

A. 3 tähte ja 3 numbrit: 26³ × 10³;

B. 4 tähte ja 3 numbrit: 26⁴ × 10³;

C. 5 tähte ja 2 numbrit: 26⁵ × 10²;

D. 2 tähte ja 6 numbrit: 26² × 10⁶;

E. 4 tähte ja 4 numbrit: 26⁴ × 10⁴.

Nende arvude välja arvutamine oleks üsna tülikas, aga seda pole ka vaja. Nimelt saame paljudel juhtudel vaadata kahe arvu jagatist ja seal sarnased liikmed välja taandada:

B / A = (26⁴ × 10³) / (26³ × 10³) = 26 > 1 (järelikult B > A);

C / B = 26/10 > 1 (järelikult C > B);

E / C = 10²/26 = 100 / 26 > 1 (järelikult E > C);

E / D = 26²/10² = (26/10)² > 1 (järelikult E > D).

4. Teisele saarele

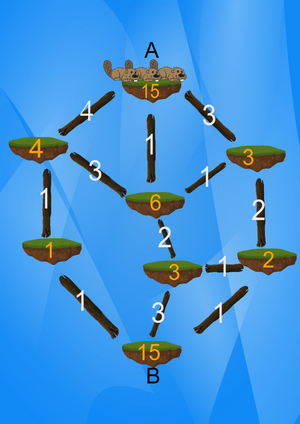
Saarel A on 15 kobrast, teised saared on tühjad.

Koprad tahavad minna peole saarele B. Kuna neil on seljas pidulikud riided, ei taha nad märjaks saada ja liiguvad mööda palke.

Kobraste grupil kulub ühe palgi ületamiseks üks minut.

Igal palgil olev arv näitab, mitu kobrast võib korraga sellel palgil olla.

Igal saarel olev arv näitab, mitu kobrast sellele saarele mahub.

Nii näiteks võib esimese minutiga liikuda 4 kobrast saarelt A all vasakul olevale saarele, 1 kobras otse all olevale saarele ja 3 kobrast all paremal olevale saarele.

Küsimus

Kui palju kopraid võib maksimaalselt olla saarel B 5 minuti pärast?

[Raadionupud]

A. 11

B. 12

C. 13

D. 14

E. 15

Vastus

Õige vastus on: C.

Vastuse selgitus

Ülesande lahendamiseks katsume seda kõigepealt lihtsustada. Pannes tähele, et iga saare kandevõime on vähemalt sama suur kui selleni viivate palkide summaarne kandevõime, võime saarte kandevõimeid üldse ignoreerida. Seega võime saarte kaardi lihtsustada all vasakul toodud skeemiks, kus iga saare kohta on kirjas sellel olevate kobraste arv ja iga palgi kohta selle kandevõime.

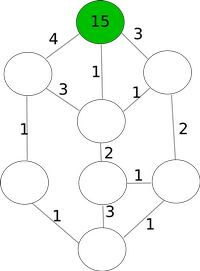
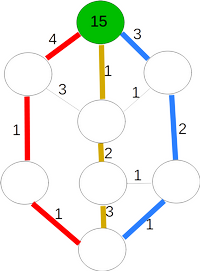
Järgmiseks võime panna tähele, et igal kopral kulub saarelt A saarele B jõudmiseks vähemalt kolm minutit. Kuna kolmel lühimal teel (ülal paremal) on igaühel vähemalt üks lõik, mille kandevõime on ainult 1 kobras, ei saa kolme minutiga saarele B jõuda rohkem kui 3 kobrast.

Kuna saarele B viivate palkide summaarne kandevõime on 5 kobrast, ei saa ühegi järgmise minutiga saarele B jõuda rohkem kui 5 kobrast. Seega on kindel, et 5 minutiga ei saa saarele B jõuda rohkem kui 3+5+5=13 kobrast.

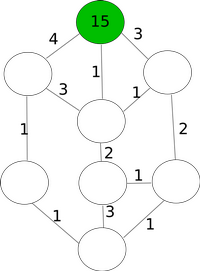
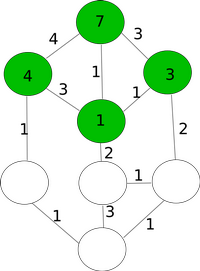
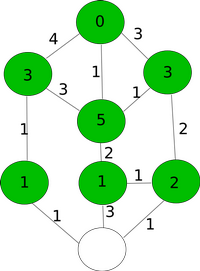
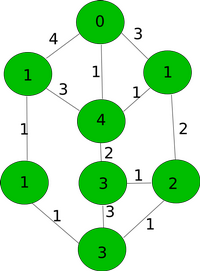
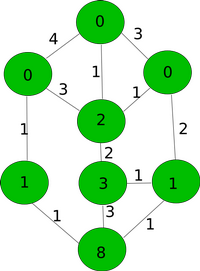
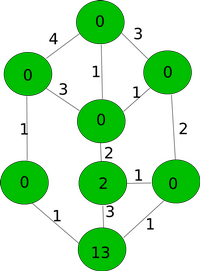
Allolevad joonised näitavad üht võimalust, kuidas 13 kobrast tõesti jõuavad 5 minutiga saarele B.

Algus	1. minut	2. minut	3. minut	4. minut	5. minut

5. Palkide tassimine

Alf ja Bob peavad mõned palgid jõe kaldalt lattu tassima. Et töö oleks lõbusam, otsustasid nad sellest teha mängu.

Nad leppisid kokku, et tassivad palke kordamööda. See, kelle kord parajasti on, valib ühe palgi ja tassib seda vasakule seni, kuni see jõuab kas lattu (joonisel vasakul) või mõne teise palgi juurde. Seal paneb ta palgi maha ja siis on teise mängija kord endale palk valida. Viimase palgi lattu tassija on kaotaja.

Me ütleme, et ühel mängijal on võitev strateegia, kui ta võib alati endale võidu kindlustada, sõltumata sellest, kui hästi või halvasti vastane mängib.

Ülalolevalt jooniselt on näha, et täna on jõe ääres neli palki. Lisaks leppsid leppisid koprad kokku, et täna alustab palkide tassimist Alf.

Kaks palki grupis A loetakse ühes kohas olevaks: kui ühte neist tassima hakata, tuleb see tassida lattu; ja kui palki B tassima hakata, siis tuleb see panna maha grupi A juures ja muutub osaks sellest grupist. Kui pärast palgi B gruppi A tassimist hakata tassima palki C, liitub ka see grupiga A.

Küsimus

Täpselt üks järgnevatest väidetest on tõene. Milline?

[Raadionupud]

A. Alfil on võitev strateegia ja võidu kindlustamiseks peaks ta esimesena tassima ühe palgi grupist A lattu.

B. Alfil on võitev strateegia ja võidu kindlustamiseks peaks ta esimesena tassima palgi B grupi A juurde.

C. Alfil on võitev strateegia ja võidu kindlustamiseks peaks ta esimesena tassima palgi C palgi B juurde.

D. Alfil ei ole võitvat strateegiat.

Vastus

Õige vastus on: B.

Vastuse selgitus

Nimetame seisuks jada, milles iga arv näitab palgigruppide suurusi lao poolt lugedes. Näiteks algseis on 211 (kuna kõik arvud on ühekohalised, ei pea me neid kuidagi eraldama).

Kui Alf tassib palgi B gruppi A (nagu väites B), siis on uus seis 31 ja edasi võib mäng jätkuda kahel moel:

Bob tassib ühe palgi grupist A lattu; siis on uus seis 21; siis tassib Alf palgi C gruppi A; siis on uus seis 3 ja sealt edasi pole muid valikuid kui palke kordamööda lattu tassida; kuna viimane palk jääb Bobile, ongi Alf võitnud.
Bob tassib palgi C gruppi A; siis on uus seis 4 ja sealt edasi pole muid valikuid kui palke kordamööda lattu tassida; kuna viimane palk jääb jälle Bobile, on Alf ikkagi võitnud.

Kuna Alfil on võitev strateegia olemas, siis väide D kindlasti õige olla ei saa.

Näitame nüüd, et ka väited A ja C pole õiged.

Kui Alf tassib ühe palgi grupist A lattu (nagu väites A), siis on uus seis 111. Siis võib Bob tassida palgi C palgi B juurde ja saada uueks seisuks 12. Seejärel võib mäng jätkuda kahel moel:

Alf tassib ühe palgi grupist B palgi A juurde, saades uueks seisuks 21; siis on seis sama, mis eelpool punktis a), aga pooled on vahetatud ja seega on nüüd võitev strateegia hoopis Bobil;
Alf tassib palgi A lattu; siis on uus seis 2 ja järgmised käigud üheselt määratud ja Bob võidab jälle.

Seega väites A kirjeldatud strateegia ei ole Alfile võitev.

Kui Alf tassib palgi C palgi B juurde (nagu väites C), on uus seis 22. Siis võib Bob tassida ühe palgi grupist A lattu ja saada uueks seisuks 12; eelnevast juba teame, et sellest seisust edasi on võitev strateegia hoopis Bobil.

6. Digikell

Digikell kasutab numbrite näitamiseks LED-indikaatoreid. Igal indikaatoril on seitse segmenti, mida saab lülitada sisse ja välja. Alloleval joonisel on näha, kuidas selliste indikaatoritega kujutatakse numbreid 0 kuni 9.

Indikaatorite segmendid kuluvad, kui nad põlevad. See segment, mis nädala jooksul kõige rohkem põleb, kulub kõige kiiremini, ja tuleb esimesena välja vahetada.

Küsimus

Milline 28-st segmendist tuleb esimesena välja vahetada?

(Kirjuta vastuseks üks number ja üks täht, nagu alloleval joonisel.)

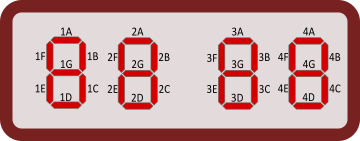
[Tekstikast]

Vastus

Õige vastus on: 1B.

Vastuse selgitus

Kell töötab ja näitab aega 24 tundi ööpäevas. See toimub nädala igal päeval samamoodi. Seega võime selle ülesande lahendamiseks nädala asemel sama hästi uurida, mis juhtub ööpäeva jooksul.

Ööpäeva jooksul näitab kell aegu 00:00 kuni 23:59. Näitest 04:01 on näha, et ühekohalisi arve näitab kell samuti kahekohalisena, lisades arvu algusse nulli.

Tundide kümneliste kohal esinevad kõigis kellaaegades ainult numbrid 0, 1 ja 2. Kõigis neis kolmes numbris on kasutusel segment B. See tähendab, et tundide kümneliste indikaatori segment B põleb ööpäevaringselt, kordagi kustumata.

See on ka ainus ööpäevaringselt põlev segment. Selles veendumiseks vaatame numbreid 1, 2 ja 5. Numbris 1 põlevad ainult segmendid B ja C. Aga numbris 2 ei põle segment C ja numbris 5 ei põle segment B. Kuna tundide ühelised ning minutite kümnelised ja ühelised kasutavad kõik numbreid 1, 2 ja 5, siis on kõigis neis indikaatorites iga segment vähemalt mingi osa ööpäevast välja lülitatud.

7. Õunakorv

Grupp inimesi püüab tagada, et korvis oleks täpselt 10 õuna.

Kui keegi neist vaatab korvi, toimib ta vastavalt sellele, mida ta korvis näeb:

Korvi sisu	Tegevus
Vähem kui 10 õuna	Lisab korvi ühe õuna
Rohkem kui 10 õuna	Eemaldab korvist ühe õuna
Täpselt 10 õuna	Ei tee midagi

Õunte loendamine toimub hetkeliselt, ilma aega kulutamata. Aga õuna korvi lisamine või selle sealt eemaldamine võtab 5 sekundit.

Inimesed üksteisega ei suhtle. Igaüks vaatab korvi ja teeb 5 sekundit hiljem vastava tegevuse teistest inimestest sõltumatult.

Alguses on korvis 9 õuna. Seejärel juhtuvad järgmised sündmused:

Aeg	Sündmus
0 sekundit	Alice vaatab korvi
4 sekundit	Bob vaatab korvi
7 sekundit	Carol vaatab korvi
8 sekundit	Dan vaatab korvi
10 sekundit	Erin vaatab korvi
11 sekundit	Frank vaatab korvi

Küsimus

Kui palju õunu lõpuks korvis on?

[Täisarv]

Vastus

Õige vastus on: 9 õuna.

Vastuse selgitus

Allolev joonis näitab sündmusi, inimeste tegevusi ja õunte arvu muutumist ajateljel:

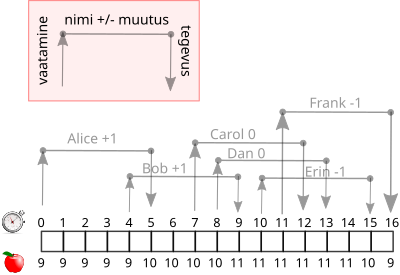
Ajatelje kohal olevad arvud näitavad sekundeid, ajatelje all on õunte arv korvis.

8. Telefoninumber

Ühes riigis on kasutusel 11-kohalised telefoninumbrid. Kuna inimesed teevad telefoninumbrite kirjutamisel ja meeldejätmisel sageli vigu, on selle riigi telefoninumbrites kasutusel järgmine süsteem:

number peab olema 7 esimese numbri (1. kuni 7.) summa viimane number.
number peab olema 4 esimese numbri (1. kuni 4.) summa viimane number.
number peab olema 1., 2., 5. ja 6. numbri summa viimane number.
number peab olema 1., 3., 5. ja 7. numbri summa viimane number.

Küsimus

Üks inimene selles riigis kirjutas üles telefoninumbri 12312316710.

Milline on õige telefoninumber, kui on teada, et inimene tegi vea täpselt ühes numbris?

(Sisesta täpselt 11 numbrit ilma tühikute või muude märkideta.)

[Tekstikast]

Vastus

Õige vastus on: 12315316710.

Vastuse selgitus

Vastuse leidmiseks vaatame kõigepealt telefoninumbri 12312316710 kontrollnumbreid:

number (6) ei sobi, sest 1+2+3+1+2+3+1 = 13.
number (7) sobib, sest 1+2+3+1 = 7.
number (1) ei sobi, sest 1+2+2+3 = 8.
number (0) ei sobi, sest 1+3+2+1 = 7.

Kui on teada, et kirjutaja tegi ainult ühe vea, ei saanud ta seda viga teha kontrollnumbrite osas, sest siin on mitu ebakõla. Järelikult peab viga olema seitsme esimese numbri hulgas.

9. number, mis on arvutatud nelja esimese numbri summana, sobib. Järelikult peavad need numbrid ka õiged olema.

Edasi näeme, et

number esineb 8., 10. ja 11. numbri arvutuses;
number esineb 8. ja 10. numbri arvutuses;
number esineb 8. ja 11. numbri arvutuses.

Kuna 8., 10. ja 11. number ükski ei sobi, peab viga olema 5. numbris, sest see on ainus, mis kõiki neid arvutusi mõjutab.

5. numbri õige väärtuse leidmiseks vaatame, milline see peaks olema, et 8. numbri arvutus õigesti välja tuleks. Peaks olema lihtne näha, et ainus sobiv väärtus on 5. Samuti on lihtne kontrollida, et selle muutuse järel tulevad õigesti välja ka 10. ja 11. numbri arvutused.

Seega peabki õige telefoninumber olema 12315316710.

9. Turniir

Täna peetakse iga-aastast kobraste turniiri. Turniiril osalevad 16 kobrast. Turniir koosneb neljast võistlusvoorust. Esimeses voorus võistlevad kõik 16 kobrast koos, aga edaspidi lähevad nende teed lahku. Iga vooru võitjad liiguvad järgmisse vooru (või oma kohale lõplikus pingereas) vasakpoolse noole suunas, kaotajad aga parempoolse noole suunas.

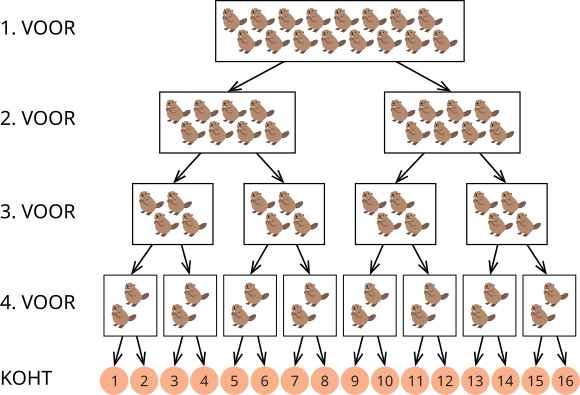
Näiteks kobras, kes võidab 1. ja 2. voorus, aga kaotab 3. ja 4. voorus, saavutab lõpuks 4. koha.

Küsimus

Noro on üks turniiril osalenutest. Millise koha ta võib saavutada, kui ta kaotab täpselt ühes voorus?

(Märgi kõik õiged vastused.)

[Märkeruudud 1..16]

Vastus

Õige vastus on: 2., 3., 5. või 9. koha.

Vastuse selgitus

Kuna turniiril on neli vooru ja Noro kaotab täpselt ühes voorus, on neli võimalikku stsenaariumi:

Ta kaotab 1. voorus ja võidab kõigis teistes voorudes. Siis liigub ta skeemis "paremale, vasakule, vasakule, vasakule" ja jõuab nii 9. kohale.
Ta kaotab 2. voorus ja võidab kõigis teistes voorudes. Siis liigub ta skeemis "vasakule, paremale, vasakule, vasakule" ja jõuab nii 5. kohale.
Ta kaotab 3. voorus ja võidab kõigis teistes voorudes. Siis liigub ta skeemis "vasakule, vasakule, paremale, vasakule" ja jõuab nii 3. kohale.
Ta kaotab 4. voorus ja võidab kõigis teistes voorudes. Siis liigub ta skeemis "vasakule, vasakule, vasakule, paremale" ja jõuab nii 2. kohale.

10. Praam

Suurel praamil on autotekil kuus rada. Äärmistele radadele A ja F mahub kummalegi 14 autot. Keskmistele radadele B, C, D ja E mahub igaühele 18 autot.

Autod sõidavad praamile järjekorranumbrite alusel ja meeskond paigutab nad tekile järgmiselt:

alguses paigutatakse autosid kordamööda radadele A ja F (esimene auto rajale A, teine auto rajale F, kolmas auto rajale A jne);
kui rajad A ja F saavad täis, hakatakse autosid paigutama kordamööda radadele B, C, D ja E (29. auto rajale B, 30. auto rajale C, 31. auto rajale D jne).

Küsimus

Millistele radadele paigutatakse järgmised autod?

[Vastavus]

A. Auto number 23

B. Auto number 47

C. Auto number 58

D. Auto number 77

Vastus

Õige vastus on: auto 23 — rajale A, auto 47 — rajale D, auto 58 — rajale C, auto 77 — rajale B.

Vastuse selgitus

Efektiivne viis selle ülesande lahendamiseks on panna tähele mustrit:

esimese 28 auto hulgas (radade A ja F täitumiseni) lähevad paaritute numbritega autod rajale A ja paarisnumbritega autod rajale F;
edasi lähevad rajale B need autod, mille järjekorranumbrid annavad 4-ga jagamisel jäägi 1; rajale C need, mis annavad jäägi 2; rajale D need, mis annavad jäägi 3 ja rajale E need, mille järjekorranumbrid jaguvad 4-ga.

Selle saab üles kirjutada ka formaalse tingimusena

kui number <= 28, siis
    kui number mod 2 == 1, siis
        rajale A
    muidu
        rajale F
muidu
    kui number mod 4 == 1, siis
        rajale B
    muidu kui number mod 4 == 2, siis
        rajale C
    muidu kui number mod 4 == 3, siis
        rajale D
    muidu
        rajale E

Siin 'X mod Y' tähendab jääki, mis tekib arvu X jagamisel arvuga Y.

11. Vihmutid

Amanda plaanib osta oma põllu kastmiseks uued vihmutid. Põld koosneb ruudukujulistest lappidest, millel kasvavad erinevad viljad, nagu näidatud alloleval kaardil.

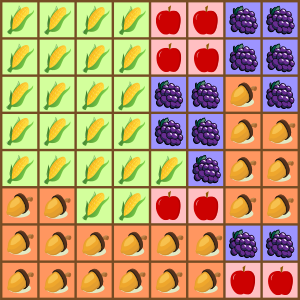
Aianduspoes müüakse vihmuteid 1×1, 2×2 ja 4×4 ruudu suuruste alade kastmiseks.

Kuna erinevaid vilju peab kastma erinevalt, ei tohi Amanda paigutada vihmuteid nii, et ühe vihmuti alla jääks mitut erinevat liiki viljadega ruute.

Samuti ei tohi ta vihmuteid paigutada nii, et mõnda ruutu kastaks mitu vihmutit või mõni vihmuti kastaks tema põllust väljapoole jäävat maad.

Küsimus

Milline on vähim arv vihmuteid, millega Amanda saab kogu oma põllu ära kasta?

[Täisarv]

Vastus

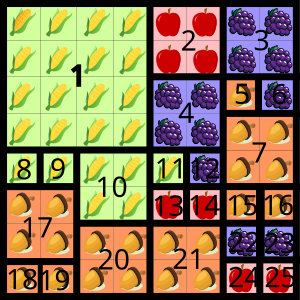
Õige vastus on: 25.

Vastuse selgitus

Vihmutite arvu vähendamiseks tuleb kasutada võimalikult palju suuremaid vihmuteid.

Amanda põllul on ainult üks 4×4 ruudu suurune ala, mis on kaetud ainult ühe viljaga (alloleval kaardil number 1).

Ülejäänud põllule mahub veel 8 vihmutit, mis kastavad 2×2 ruudu suuruseid alasid (alloleval kaardil numbrid 2, 3, 4, 7, 10, 17, 20, 21).

Ülejäänud 16 ruutu (8×8 [terve põld] - 1×(4×4) [üks 4×4 vihmuti] - 8×(2×2) [kaheksa 2×2 vihmutit]) tuleb katta 1×1 vihmutitega.

Kokku on seega vaja 1 + 8 + 16 = 25 vihmutit.

12. Piletiautomaat

Lõbustuspargis tuleb "Ameerika mägedele" piletit ostes sisestada müügiautomaati ostja sünnikuupäev ja pikkus, sest sinna lubatakse sõitma ainult külalisi, kes on vähemalt 13 aastat vanad ja vähemalt 120 cm pikad.

Piletiautomaadi sees on valem, mis kontrollib ostja sisestatud andmete vastavust tingimustele. Näiteks 4. veebruaril 2024 peaks valem tegema järgmised otsused:

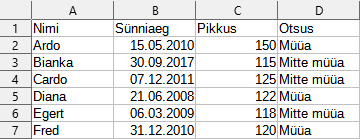
Valemis võivad lisaks matemaatilistele tehetele (+, -, *, /) ja võrdlustele (>, <, >=, <=) olla kasutusel järgmised funktsioonid:

Funktsioon	Tähendus
`IF(X; Y; Z)`	Väärtus Y, kui tingimus X kehtib; väärtus Z, kui tingimus X ei kehti
`AND(X; Y)`	Tingimus, mis kehtib siis, kui kehtivad nii tingimus X kui ka tingimus Y
`OR(X; Y)`	Tingimus, mis kehtib siis, kui kehtib kas tingimus X või tingimus Y või tingimused X ja Y mõlemad
`NOW()`	Tänane kuupäev
`EDATE(X; Y)`	Kuupäev, mis saadakse, kui kuupäevale X liita Y kuud (kuupäevast X tulevikus, kui Y on positiivne; minevikus, kui negatiivne)

Küsimus

Millised järgmistest valemitest võiksid olla tabeli lahtris D2, et lahtrites B2 ja C2 andmete muutmisel tehtaks alati õige otsus?

(Märgi kõik õiged vastused.)

[Märkeruudud]

A. =IF(AND(EDATE(NOW();-13*12)>=B2;C2>=120);"Müüa";"Mitte müüa")

B. =IF(OR(EDATE(NOW();-13*12)>=B2;C2>=120);"Müüa";"Mitte müüa")

C. =IF(AND(EDATE(NOW();-13*12)<B2;C2>=120);"Müüa";"Mitte müüa")

D. =IF(OR(EDATE(NOW();-13*12)>=B2;C2<120);"Mitte müüa";"Müüa")

E. =IF(AND(EDATE(NOW();-13*12)<B2;C2<120);"Mitte müüa";"Müüa")

F. =IF(OR(EDATE(NOW();-13*12)<B2;C2<120);"Mitte müüa";"Müüa")

Vastus

Õige vastus on: A, F.

Vastuse selgitus

Variant A on õige, sest

EDATE(NOW();-13*12) leiab kuupäeva, mis on tänasest 13×12 kuud ehk 13 aastat tagasi;
EDATE(NOW();-13*12)>=B2 kontrollib, et ostja sünnikuupäev on sellega võrdne või sellest varasem;
C2>=120 kontrollib, et ostja pikkus on 120 cm või sellest suurem;
AND(EDATE(NOW();-13*12)>=B2;C2>=120) kontrollib, et kaks eelmist tingimust mõlemad kehtivad;
IF(AND(EDATE(NOW();-13*12)>=B2;C2>=120);"Müüa";"Mitte müüa") väljastab otsuse "Müüa" parajasti siis, kui mõlemad tingimused kehtivad.

Variant B ei ole õige, sest väljastab otsuse "Müüa", kui ostja rahuldab vähemalt üht kahest nõutud tingimusest; see tähendab, see valem lubab pileti müüa ka siis, kui ostja on küll piisavalt vana, aga liiga lühike, ja ka siis, kui ostja on küll piisavalt pikk, aga liiga noor.

Variant C ei ole õige, sest vanuse tingimus on valepidi; see valem lubab pileti müüa, kui ostja on vähemalt 120 cm pikk ja noorem kui 13 aastat.

Variant D väljastab otsuse "Mitte müüa", kui ostja on vähemalt 13 aastat vana või lühem kui 120 cm; see tähendab, et see valem lubab pileti müüa ainult siis, kui ostja on noorem kui 13 aastat ja vähemalt 120 cm pikk; tuleb välja, et see valem näeb küll väga erinev välja, aga arvutab täpselt sama tingimust kui variant C!

Variant E ei ole õige, sest see on samaväärne variandiga B, sarnaselt D ja C samaväärsusele.

Variant F on õige, sest see on samaväärne variandiga A, sarnaselt D ja C samaväärsusele.

13. Teksti parandamine

Lihtsas tekstitöötlusprogrammis lisab täheklahvi vajutamine vastava tähe kursorist vasakule ja lisaks on võimalik kasutada mõningaid eriklahve, nagu näidatud allpool.

	Klahv "←" viib kursori ühe tähe võrra vasakule.
	Klahv "→" viib kursori ühe tähe võrra paremale.
	Klahv "bksp" kustutab kursorist vasakul oleva tähe.
	Klahv "del" kustutab kursorist paremal oleva tähe.
	Klahv "home" viib kursori rea algusse.
	Klahv "end" viib kursori rea lõppu.

Küsimus

Sidevigade tõttu muutusid teksti "abcdefghijklm" edastamisel mõned tähed tärnideks "*".

Milline on vähim klahvivajutuste arv, millega saab esialgse teksti taastada?

[Täisarv]

Vastus

Õige vastus on: 13.

Vastuse selgitus

Lahenduse leidmiseks vaatame kõigepealt ülesande lihtsamat varianti, kus riknes ainult üks täht:

Selle vea parandamiseks tuleb kõigepealt kursor tärni kõrvale liigutada, siis tärn ära kustutada ja siis õige täht asemele sisestada.

Võime tärni juurde liikuda "←"-klahviga. Sel juhul kulub 7 klahvivajutust, et kursor oleks tärnist paremal. Siis saame "bksp"-klahviga tärni ära kustutada ja "f"-klahviga õige tähe sisestada. Kokku kulub 9 klahvivajutust.

Teine variant on liikuda "home"-klahviga rea algusse ja siis "→"-klahviga tärni juurde. Sel juhul kulub 6 klahvivajutust, et kursor oleks tärnist vasakul. Siis saame "del"-klahviga tärni ära kustutada ja "f"-klahviga õige tähe sisestada. Kokku kulub 8 klahvivajutust.

Peaks olema ilmne, et kõik muud võimalikud lahendused teevad nende kahega võrreldes liigseid klahvivajutusi ja seega ei saa olla optimaalsed.

Tagasi ülesande täisvariandi juurde liikudes näeme, et eelnevale lisaks on vaja kustutada ja õigete tähtedega asendada ka kolm sõna lõpus olevat tärni. Selleks kulub 3 "bksp"-klahvi ja 3 täheklahvide vajutust, kokku 6 klahvivajutust.

Tehes need 6 klahvivajutust ja nende järel eelpool leitud 8 klahvivajutust, saaksime kokku 14 klahvivajutusega lahenduse. Aga see pole veel optimaalne.

Nimelt saame ära kasutada asjaolu, et "bksp"-klahvi abil sõna lõpus olevate tärnide kustutamise järel on kursor sõna keskel olevale tärnile lähemal kui enne või pärast. Sel hetkel on meil võimalik keskmise tärni juurde liikuda 4 "←"-klahvi vajutusega, siis "bksp"-klahviga tärn ära kustutada, "f"-klahviga õige täht sisestada ja "end"-klahviga taas sõna lõppu naasta. Kokku kulub selleks manöövriks 7 klahvivajutust. (Seekord oleks "home"-klahviga rea algusse liikumine kulukam.)

Kombineerides 3 "bksp"-klahvi vajutust, 7 klahvivajutusega manöövri eelmisest lõigust ja 3 täheklahvide vajutust, saame kokku 13 klahvivajutusega lahenduse. Kuna sõna lõpus olevate tärnide parandamiseks kulub igal juhul 6 klahvivajutust ja igast muust seisust peale eelmises lõigus vaadeldu kuluks sõna keskel oleva tärni juurde jõudmiseks ja selle parandamiseks rohkem klahvivajutusi, on leitud 13 klahvivajutusega lahendus ka parim võimalik.

14. Pildi vähendamine

Koprad kasutavad piltide vähendamiseks järgmist meetodit:

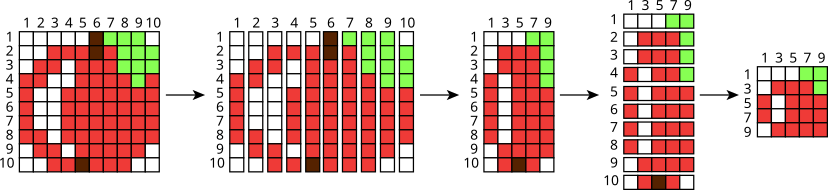
Esiteks lõikavad nad pildi vertikaalselt kümneks võrdse laiusega ribaks. Seejärel kleebivad nad paaritute numbritega ribad kokku uueks pildiks.

Siis lõikavad nad uue pildi horisontaalselt kümneks võrdse laiusega ribaks. Seejärel kleebivad nad paaritute numbritega ribad kokku lõplikult pildiks.

Küsimus

Milline on tulemus, kui allolevat pilti selle meetodiga vähendada?

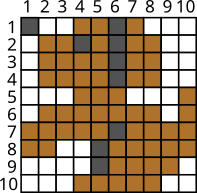
[Raadionupud]

Vastus

Õige vastus on: B.

Vastuse selgitus

Meetodi rakendamine sammude kaupa:

15. KopraGPT

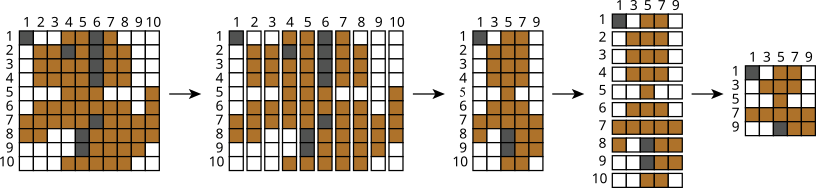
KopraGPT on lihtne keelemudel kolmesõnaliste lausete genereerimiseks. Lause genereerimisel valitakse iga järgmine sõna juhuslikult, kusjuures erinevate valikute tõenäosused sõltuvad eelnevalt valitud sõnadest. Allolevad tabelid näitavad tõenäosusi mõnede võimalike lausealguste jaoks.

Teise sõna valimine vastavalt esimesele:

Algus	"armastavad"	"vihkavad"
"Kassid"	0,7	0,3
"Koprad"	0,6	0,4

Kolmanda sõna valimine vastavalt kahele esimesele:

Algus	"ujumist"	"jooksmist"
"Kassid armastavad"	0,2	0,8
"Kassid vihkavad"	0,9	0,1
"Koprad armastavad"	0,7	0,3
"Koprad vihkavad"	0,1	0,9

Näiteks, kui anda esimeseks sõnaks "Kassid", siis on lause "Kassid armastavad jooksmist" saamise tõenäosus 0,56, sest

sõna "Kassid" järel teiseks sõnaks "armastavad" valimise tõenäosus on 0,7;
sõnapaari "Kassid armastavad" järel kolmandaks sõnaks "jooksmist" valimise tõenäosus on 0,8;
kuna mudel teeb need valikud üksteise järel, on nende mõlema tegemise tõenäosus kokku 0,7 × 0,8 = 0,56.

Küsimus

Milline KopraGPT väljund on kõige tõenäolisem, kui esimeseks sõnaks anda "Koprad"?

[Raadionupud]

A. "Koprad vihkavad ujumist"

B. "Koprad vihkavad jooksmist"

C. "Koprad armastavad ujumist"

D. "Koprad armastavad jooksmist"

Vastus

Õige vastus on: C.

Vastuse selgitus

Vastusevariantide tõenäosused on järgmised:

"Koprad vihkavad ujumist": 0,4 × 0,1 = 0,04,
"Koprad vihkavad jooksmist": 0,4 × 0,9 = 0,36,
"Koprad armastavad ujumist": 0,6 × 0,7 = 0,42,
"Koprad armastavad jooksmist": 0,6 × 0,3 = 0,18.

Natuke saaks arvutamist kokku hoida sellega, et panna tähele, et lause alguse "Koprad vihkavad" korral on lõpp "jooksmist" tõenäolisem kui lõpp "ujumist" ja siis "Koprad vihkavad ujumist" ei saa kindlasti kõige tõenäolisem lause olla ja siis selle tõenäosust välja arvutada pole vaja. Samamoodi võib jätta arvutamata ka lause "Koprad armastavad jooksmist" tõenäosuse.

Flag icons by GoSquared.