

Dodol on kaks puuviljakasti, X ja Y. Mõlemad kastid on jagatud kümneks nummerdatud lahtriks. Kastide mõnedes lahtrites on õunad  , teistes apelsinid
, teistes apelsinid  .
.
Dodo võib puuviljade muutmiseks kasutada kaht liiki käske:
vaheta[m,n]: Kasti X lahtrites m kuni n olevad puuviljad liiguvad samade numbritega lahtritesse kasti Y. Samal ajal liiguvad kasti Y lahtrites m kuni n olevad puuviljad samade numbritega lahtritesse kasti X.
muuda[m,n]: Mõlema kasti lahtrites m kuni n muutuvad õunad apelsinideks ja apelsinid õunteks.
Olgu näiteks alguses kastides sellised puuviljad:
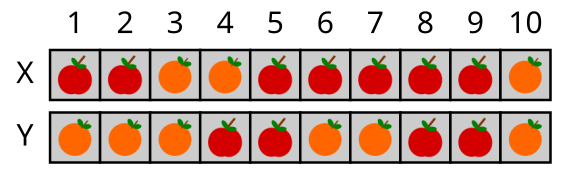
Siis on käsu vaheta[3,8] tulemus selline:
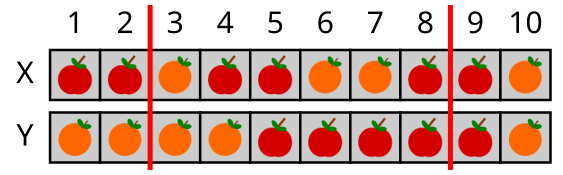
Kui pärast seda anda käsk muuda[3,6], siis saame:
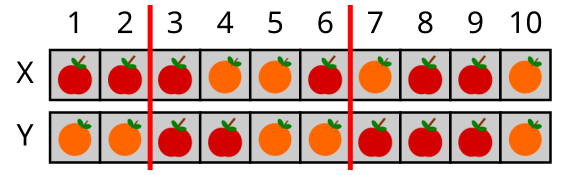
Oletame nüüd, et alguses on kastides sellised puuviljad:

ja Dodo annab järjest käsud muuda[5,7], vaheta[2,5] ja muuda[7,10].
Kui palju on lõpuks õunu kastis X rohkem kui kastis Y?
[Täisarv]
Õige vastus on: 2.
Algseis:

Käsu muuda[5,7] järel:
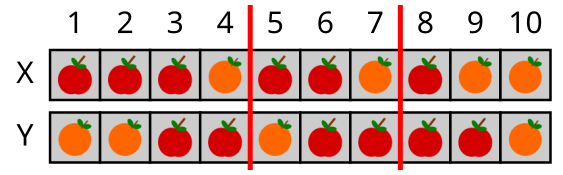
Käsu vaheta[2,5] järel:

Käsu muuda[7,10] järel:
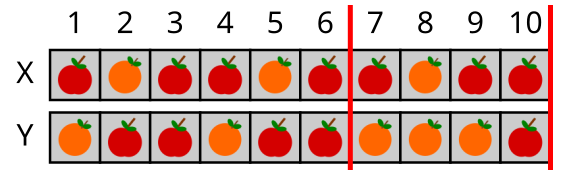
Seega on lõpuks kastis X 7 õuna ja kastis Y 5 õuna, ehk kastis X on 2 õuna rohkem kui kastis Y.

Robot  tahab jõuda oma lähtekohast kopra
tahab jõuda oma lähtekohast kopra  juurde.
juurde.
Robot liigub vastavalt tema all olevatele värvilistele kujunditele:
 = astu otse edasi;
= astu otse edasi; = pööra paremale ja astu siis edasi;
= pööra paremale ja astu siis edasi; = pööra vasakule ja astu siis edasi.
= pööra vasakule ja astu siis edasi.Pane tähele, et me ei näe, milline kujund on roboti all tema lähtekohas.
Näiteks, kui alloleval kaardil oleks roboti all roheline kolmnurk, siis liiguks robot kopra juurde üle kujundite  nooltega näidatud teed mööda: esimesel sammul pööraks vasakule ja astuks edasi; teisel sammul pööraks paremale ja astuks edasi; kolmandal sammul astuks otse edasi ja jõuakski kohale.
nooltega näidatud teed mööda: esimesel sammul pööraks vasakule ja astuks edasi; teisel sammul pööraks paremale ja astuks edasi; kolmandal sammul astuks otse edasi ja jõuakski kohale.

Millise kujundite jada kaudu jõuaks robot kopra juurde alloleval kaardil?

[Raadionupud]
A. 
B. 
C. 
D. 
Õige vastus on: C.
Kui roboti lähtekohas on roheline kolmnurk, siis liigub ta üle variandis C näidatud kujundite alloleval kaardil nooltega näidatud teed mööda.
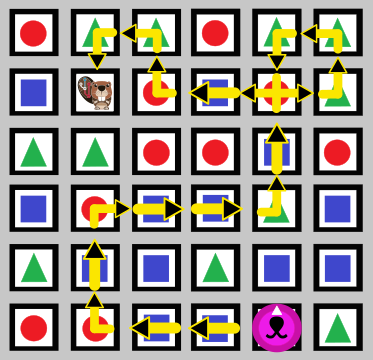
Variant A ei saa olla õige vastus, sest kui roboti lähtekohas oleks roheline kolmnurk, siis liiguks ta selle variandi järgi kuni allpool ristiga märgitud punase ringini. Seal aga tekiks vastuolu, sest paremale pööramise järel astuks ta sinise ruudu asemel rohelise kolmnurga peale.

Variant B ei saa olla õige vastus, sest kui roboti lähtekohas oleks punane ring, siis liiguks ta selle variandi järgi kuni allpool ristiga märgitud punase ringini. Seal aga tekiks vastuolu, sest paremale pööramise järel astuks ta märgitud alalt välja ja ei saaks enam juhiseid, kuidas edasi liikuda.

Variant D ei saa olla õige vastus, sest kui roboti lähtekohas oleks sinine ruut, siis jõuaks ta selle variandi järgi liikudes tagasi oma lähteruudu kõrvale, mitte kopra juurde.
Teine võimalus valede variantide välistamiseks on selline:
Variandid B ja D ei saa olla õiged, sest nendes variantides on viimane kujund sinine ruut. Kopra kõrval on ainult üks sinine ruut, aga selle pealt robot kopra juurde jõuda ei saa, sest sinise ruudu peal robot ei pööra ja järelikult peaks ta koprani jõudmiseks astuma sinise ruudu peale vasakult, see tähendab väljastpoolt märkidega ala.
Variant A ei saa ka õige olla, sest ainuke punane ring kopra kõrval on koprast paremal. Selle ringi pealt koprani jõudmiseks peaks robot astuma ringi peale ülevalt, rohelise kolmnurga pealt. Selleks omakorda peaks robot astuma rohelise kolmnurga peale paremalt, teise punase ringi pealt. Ja selleks omakorda peaks ta selle punase ringi peale astuma ülevalt, mis oleks jälle väljastpoolt märkidega ala.
Seega ei saa ükski teine variant peale C olla õige vastus.

Kobrastel on masin, mis teeb raami sisse õhupallidest kujundeid.
Alguses on kõik pallid tühjad:

Kui mõne palli juures olevat nuppu vajutada, puhub masin selle täis. Masin lõpetab puhumise, kui pall puutub raami vastaskülge või mõnda teist palli.
Näiteks, kui vajutada nuppu E ja siis nuppu C, on tulemus selline:

Millises järjekorras peaks nuppe vajutama, et saada allolev kujund?
[Interaktiivne]
(Lohista nupud hallidesse ringidesse õigesse järjekorda.)
Võimalikud õiged vastused: BAECD, BEACD, BECAD, BECDA.
Lahenduse leidmiseks paneme tähele, et ball B tuleb täis puhuda enne palli A: palli A puhumine on peatunud, sest pall B jäi sellele ette.
Samamoodi tuleb pall B täis puhuda enne palli E, pall E enne palli C ja pall C enne palli D.
See tähendab, et pallid B, E, C, D tuleb täis puhuda täpselt selles järjekorras ja palli A võib täis puhuda ükskõik millal pärast palli B.
Palli A lisamiseks B, E, C, D hulka nii, et see oleks pärast palli B, ongi täpselt neli võimalust:

Koprapoeg Todd sai kingi, mille pakend on kokku kleebitud viiest erineva kujundusega paberilehest:

Millisena paistab lahti volditud pakend selle põhja poolt vaadates?
[Raadionupud]
A.  B.
B.  C.
C.  D.
D. 
Õiged vastus on: B.
Vastusevariant B on ainus, kus kõik värvid ja mustrid asetsevad üksteise suhtes õigesti:
Kaht ülejäänud külge ei ole algsel pildil näha, seega nende kohta me tegelikult ei tea midagi.
Variant A ei saa olla õige, sest pakendi põhi peaks olema punasetriibuline, mitte mustatäpiline.
Variant C ei saa olla õige, sest tumesinisest küljest vasakul peaks olema heleroosa külg.
Variant D ei saa olla õige, sest tumesinine külg peaks olema pakendi põhja triipude otstes ja tumesinisest küljest vasakul peaks olema heleroosa külg.

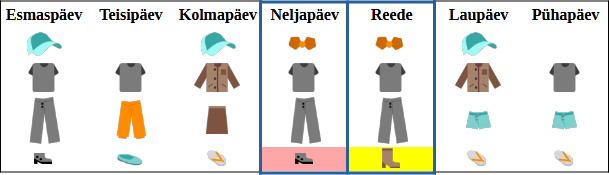
Veronikal on palju riideid. Tavaliselt kannab ta igal nädalapäeval kindlat riiete komplekti:
| Esmaspäev | Teisipäev | Kolmapäev | Neljapäev | Reede | Laupäev | Pühapäev |
|---|---|---|---|---|---|---|
 |
 |
 |
 |
 |
||
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Peole minnes riietus Veronika tavalisest erinevalt. Üks sõber kirjeldas Veronika peoriietust, võrreldes seda tema tavaliste komplektidega.
Mida Veronika peol kandis?
[Interaktiivne]
(Lohista igasse roosasse kasti üks riideese nii, et kõik neli väidet oleks õiged.)
Õige vastus on:  ,
,  ,
,  ,
,  .
.
 on ainus asi, mida Veronika kannab nii esmaspäeval kui kolmapäeval:
on ainus asi, mida Veronika kannab nii esmaspäeval kui kolmapäeval: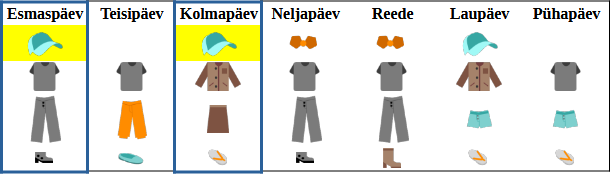
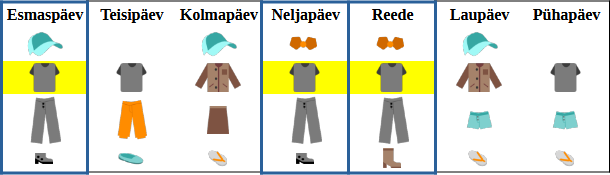
 kannab Veronika esmaspäeval, neljapäeval ja reedel; ainus teine asi, mida ta ka kõigil neil päevadel kannab, on
kannab Veronika esmaspäeval, neljapäeval ja reedel; ainus teine asi, mida ta ka kõigil neil päevadel kannab, on  :
:
 ja
ja  ; oluline on siin sõbra väites olev sõna "ainult", sest
; oluline on siin sõbra väites olev sõna "ainult", sest  kannab Veronika ka kolmapäeval; seega peab vastus olema
kannab Veronika ka kolmapäeval; seega peab vastus olema  :
:
 :
:

Oliveril on läbipaistva kesta ja värviliste kuulidega kõristi.
Kui ta kõristit raputab, veerevad mõned kuulid selles teise poolde:
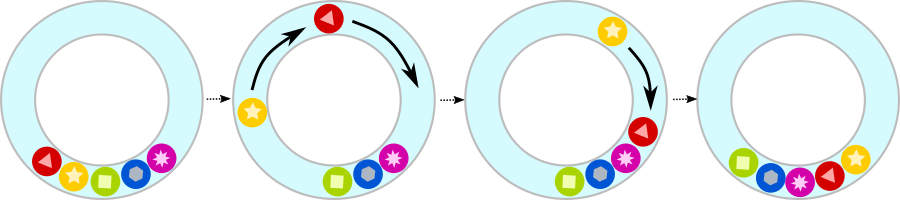
Nüüd raputas Oliver oma kõristit veel korra. Kuidas kuulid nüüd paiknevad?
[Interaktiivne]
(Lohista kuulid kõristisse nende õigetele kohtadele.)
Õige vastus on:  .
.
Ülesande lahendamiseks peame tähele panema, et kui kuulid kõristis veerevad, jääb nende omavaheline järjekord samaks: vastupäeva lugedes tuleb punase kuuli  järel alati kollane
järel alati kollane  , kollase järel roheline
, kollase järel roheline  , rohelise järel sinine
, rohelise järel sinine  ja sinise järel lilla
ja sinise järel lilla  kuul.
kuul.
Küsimuses on rohelise kuuli järel üks tühi koht. Kui kõristit veel raputada, tuleks selle koha järele omakorda lilla kuul. Rohelise ja lilla kuuli vahel peab olema sinine kuul.
Samamoodi edasi mõeldes saame, et kahte lilla kuuli järel olevasse tühja kohta peavad käima punane ja kollane kuul, punane kuul lilla ja kollane kuul rohelise kõrvale.

Neli looma matkasid läbi kõrbe ja märkisid oma teekonnad kaardile.
Kahjuks on kaardi keskmine osa kaduma läinud:

Milline järgnevatest võiks olla selle kaardi keskmine osa?
[Raadionupud]
A.  B.
B. 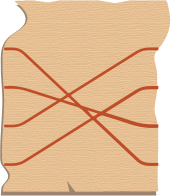 C.
C. 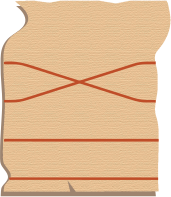 D.
D. 
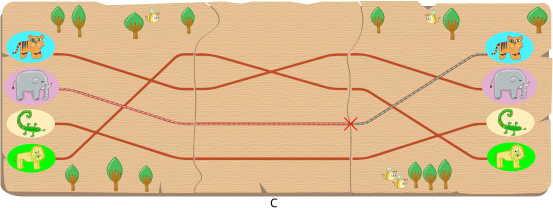
Õige vastus on: D.
Kui paneme variandis D kujutatud osa kaardi keskele, on igal joonel mõlemas otsas sama loom:
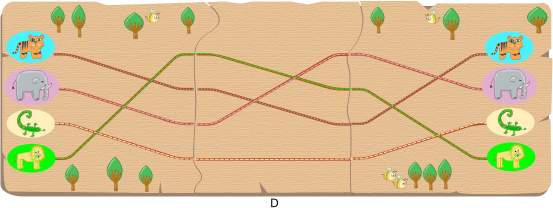
Variandi A korral jõuaks näiteks tiiger matka lõpuks kohale sisalikuna:
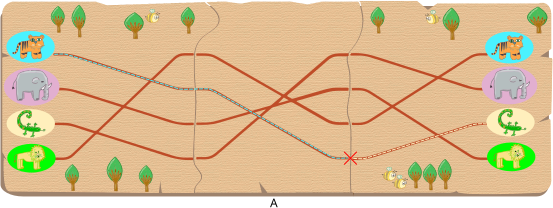
Variandi B korral jõuaks näiteks lõvi matka lõpuks kohale sisalikuna:
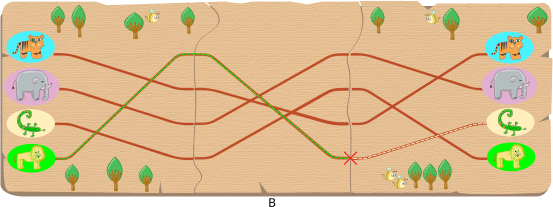
Variandi C korral jõuaks näiteks elevant matka lõpuks kohale tiigrina:

Mõned Põhja-Aafrika berberite hõimud kasutavad tifanaghi tähestikku. Tim kasutab seda tähestikku salakirjana.
Ta seadis ladina tähestiku igale tähele vastavusse ühe tifanaghi tähestiku tähe ja kodeeris nii viis sõna: BEBRAS, TURTLE, WEASEL, WALRUS ja IGUANA.
Millised ladina tähestikus kirjutatud sõnad vastavad tifanaghi tähestikus kirjutatud koodidele?
[Interaktiivne]
(Lohista ladina tähestikus sõnad neile vastavate koodide kõrvale.)
Õige vastus on:  .
.
Esimesena võib tekkida mõte eristada sõnu nende pikkuste järgi. Kahjuks aga sellest abi ei ole, sest need on kõik 6-tähelised!
Seega tuleb hakata uurima tähtede esinemise mustreid. Võime näiteks panna tähele, et sõnas BEBRAS on esimene ja kolmas täht samad. Ainus sama mustriga kood on  ja järelikult käivad need kokku.
ja järelikult käivad need kokku.
Seega peab E-tähele vastama kood  ja A-tähele kood
ja A-tähele kood  ning nende järgi saame leida vasted ka ülejäänud sõnadele.
ning nende järgi saame leida vasted ka ülejäänud sõnadele.
Sõna WEASEL on ainus, kus on kaks E-tähte, ja kood  on ainus, kus
on ainus, kus  esineb kaks korda, järelikult käivad need kokku.
esineb kaks korda, järelikult käivad need kokku.
Sõna TURTLE on ainus, mis lõppeb E-tähega, ja kood  on ainus, mille lõpus on
on ainus, mille lõpus on  , järelikult käivad need kokku.
, järelikult käivad need kokku.
Sõna IGUANA on ainus, milles on kaks A-tähte, ja kood  on ainus, kus
on ainus, kus  esineb kaks korda, järelikult käivad need kokku.
esineb kaks korda, järelikult käivad need kokku.
Sõna WALRUS on ainus, milles teine täht on A, ja kood  on ainus, kus teisel kohal on
on ainus, kus teisel kohal on  , järelikult käivad need kokku.
, järelikult käivad need kokku.
Muidugi on võimalikud ka teised arutluskäigud.

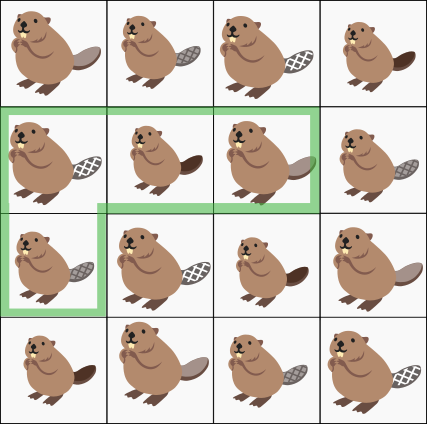
Nelja liiki koprad tuleb paigutada ruudustikku nii, et
Milline kobras peab olema küsimärgiga ruudus?

[Raadionupud]
A.  B.
B.  C.
C.  D.
D. 
Õige vastus on: A.
Laheduse leidmiseks on kaks võimalust.
Esimene võimalus on panna tähele, et ruudustiku kolmandas reas on juba olemas koprad A, D ja C ning järelikult peab kolmandas reas esimeses veerus olema kobras B. Siis on aga esimeses veerus juba olemas koprad C, B, ja D ning järelikult peab esimeses veerus teises reas olema kobras A.
Teine võimalus on rakendada sama loogikat kõigepealt teises ja kolmandas veerus ning järeldada, et teises veerus teises reas peab olema kobras D ja kolmandas veerus teises reas kobras C. Siis on teises reas juba olemas koprad D, C ja B ning ka sellest arutlustest järeldub, et teises reas esimeses veerus peab olema kobras A.
Nende kahe arutluskäiguga saame täita kõik tühjad ruudud:


Igor, Mati, Tom ja Rolf on neli sõpra. Neil on kõigil erinevad ametid: pagar, õpetaja, arhitekt ja juuksur.
Me teame sõprade kohta järgmist:
Mis ametit iga sõber peab?
[Interaktiivne]
(Lohista iga amet õige nime juurde.)
Õige vastus on:  .
.
Kui juuksur, õpetaja ja Mati käisid esmaspäeval koos rallit vaatamas, siis tähendab see, et Mati pole ei juuksur ega õpetaja. Samamoodi järeldame teisipäevast, et Igor ega Rolf pole õpetajad ning kolmapäevast, et Igor ega Mati pole pagarid.
Ülevaatlikkuse mõttes võime need andmed tabelisse panna:
| Amet | Igor | Mati | Tom | Rolf |
|---|---|---|---|---|
| Pagar | - | - | ||
| Õpetaja | - | - | - | |
| Arhitekt | ||||
| Juuksur | - |
Nüüd on hästi näha, et ei Igor, Mati ega Rolf pole õpetajad. Järelikult peab õpetaja olema Tom. Ja siis ei ole tal muid ameteid.
Samuti on näha, et Mati pole pagar, õpetaja ega juuksur ja järelikult peab ta olema arhitekt ja järelikult keegi teine arhitekt ei ole.
Kui lisame ka need andmed tabelisse:
| Amet | Igor | Mati | Tom | Rolf |
|---|---|---|---|---|
| Pagar | - | - | - | |
| Õpetaja | - | - | + | - |
| Arhitekt | - | + | - | - |
| Juuksur | - | - |
siis on kohe näha, et Igor peab olema juuksur ja Rolf pagar.

Lukas, Emma, Filipp, Nelli ja Samuel sündisid kõik sama aasta kevadel, aga erinevatel päevadel.
Lisaks teame, et:
Mis kuupäeval iga laps sündis?
[Interaktiivne]
(Lohista iga kuupäev õige nime juurde.)
Õige vastus on:  .
.
Me teame, et Emma on 5 päeva vanem kui Samuel. Ainsad kaks kuupäeva, mille vahe on täpselt 5 päeva, on 29. aprill ja 4. mai. Seega peab Samuel olema sündinud 4. mail ja Emma 29. aprillil.
Edasi teame, et Filipp on sündinud aprillis. Kuna 29. aprill on juba Emma sünnipäev, peab Filipp olema sündinud 4. aprillil.
Kuna Lukas on vanem kui Filipp, peab tema olema sündinud 17. märtsil. Nelli sünnipäevaks jääb alles ainult 1. mai.

Aplikatsioon on tehnika, kus kangale õmmeldakse peale erinevaid kujundeid.
Ühel õmblejal on kahte liiki kujundeid: elevandid ja lilled. Oma töö lihtsustamiseks jagab ta nii kujundid kui kangad ruutudeks. Nii on näha, et elevant võtab 5×5 ja lill 3×3 ruutu.

Õmbleja võib mõlema kanga peale õmmelda mõlemat liiki kujundeid, aga need ei tohi üksteist katta ega üle kanga ääre välja ulatada. Ta tahab õmmelda kangastele kõigepealt nii palju elevante kui võimalik ja pärast seda nii palju lilli kui võimalik.
Kui palju kujundeid ta kahe kanga peale kokku õmmelda saab?
[Raadionupud]
A. 8 (3 elevanti ja 5 lille)
B. 9 (3 elevanti ja 6 lille)
C. 10 (4 elevanti ja 6 lille)
D. 10 (3 elevanti ja 7 lille)
Õige vastus on: B.
Üks võimalus 9 kujundi paigutamiseks on alloleval joonisel.

Võimalikud on ka teised paigutused. Näiteks võib mõlemal kangal paremal üleval olevat lille paigutada allapoole või roosal kangal elevante paremale nihutada ja ülemise lille neist vasakule või nende vahele panna. Aga kõigis neis paigutustes on kujundite arv sama.
Rohkem kujundeid paigutada ei saa, sest:

Copyright © 2024 Bebras – International Challenge on Informatics and Computational Thinking.
Licensed under Creative Commons Attribution-ShareAlike 4.0 International License.
Flag icons by GoSquared.