
Ühes mängus moodustatakse ridasid A-, B- ja C-tähtedega kaartidest. Kui mängija kaardireas on kaks sama tähega kaarti kõrvuti, saab ta selle eest 2 punkti; kui kõrvuti on kolm sama tähega kaarti, saab selle eest 3 punkti; ja nii edasi, vastavalt korduste arvule.
Näiteks allolev hallide kaartide rida annaks 0 punkti, sest selles pole kuskil mitut sama tähte kõrvuti. Aga mängija saab oma tulemust parandada kahe punase kaardi abil.

Kui ta katab esimese halli C-kaardi punase A-kaardiga ja teise halli C-kaardi punase B-kaardiga, nagu alloleval joonisel, saab ta kahe kõrvutioleva A-kaardi eest 2 punkti ja kahe kõrvutioleva B-kaardi eest samuti 2 punkti. Üksik B-kaart endiselt punkte ei anna, seega saab mängija kokku 2+2=4 punkti.

Kuidas peaks mängija allolevas seisus oma punaseid kaarte kasutama, et parim võimalik tulemus saada?
[Interaktiivne]
(Lohista punased kaardid õigetesse kohtadesse hallide kaartide peale.)
Kobras Harry uurib saarestikku, milles mõned saared on omavahel sildadega ühendatud. Ta tahaks kõik saared läbi käia.
Igalt saarelt näeb ta kõiki selle naabersaari ja ka seda, millistel neist on märgid.
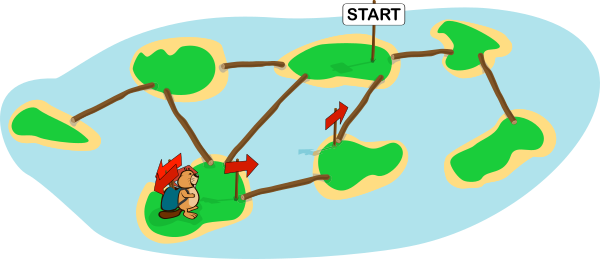
Joonisel on olukord, kus Harry alustas saarelt märgiga START ja on juba jõudnud veel kahele saarele.
Milliste juhiste järgi peaks ta käituma, et kindlasti kõiki saari külastada?
[Interaktiivne]
(Lohista juhistes olevatesse lünkadesse õiged käsud.)
Kobrastel on masin, mis teeb raami sisse õhupallidest kujundeid.
Kui mõne palli juures olevat nuppu vajutada, siis:
Näiteks, kui kõik pallid on tühjad ja siis vajutada nuppe F, A, B, A, on tulemus selline:

Millises järjekorras peaks nuppe vajutama, et saada tühjade pallidega masinasse üheksa nupuvajutusega allolev kujund?
[Interaktiivne]
(Lohista nupud tühjadesse ringidesse õigesse järjekorda.)
Kobras Castor õpetab lapsi lugema ja kasutab selleks erinevaid mänge. Üks neist on sõnajadade loomine.
Sõnajadas peab iga järgmise sõna saamiseks eelmises muutma täpselt ühte tähte. Näiteks MUG → MUD → MAD → FAD on sõnajada.

Castoril on järgmised üheksa sõna: BAD, BAT, BOT, CAB, CAT, COB, COT, SAD ja SAT. Ta jagab need kolmeks sõnajadaks nii, et igas jadas on kolm sõna ja iga sõna on kasutusel täpselt ühes jadas.
Milline järgmistest EI SAA olla Castori kolme jada hulgas?
Kõik need variandid on korrektsed sõnajadad. Aga neist üks on selline, et ülejäänud kuuest sõnast ei saa enam kahte ülejäänud jada moodustada.
[Raadionupud]
A. BAT → CAT → COT
B. CAT → CAB → COB
C. COT → COB → CAB
D. SAD → BAD → BAT
Bob palgati Ringjärve paadisildu kontrollima. Selleks peab ta mööda kallast iga paadisilla juurde kõndima. Tal on üsna raske tööriistakast, sellepärast tahab ta kokku võimalikult lühikese maa läbi käia.
Bob võib iga paadisilla juurest minna kas päripäeva või vastupäeva järgmise juurde. Muidugi võib ta järgmise veel kontrollimata paadisilla juurde jõudmiseks juba kontrollitud paadisildadest uuesti mööda kõndida.
Kui Bob on kõik paadisillad üle vaadanud, tellib ta viimasena kontrollitud paadisilla juurde takso ja sõidab sealt otse koju.
Joonisel on näha Ringjärve paadisillad ja nendevahelised kaugused ning Bobi lähtekoht.

Milline on vähim vahemaa, mille Bob peab läbi käima, et kõik paadisillad üle vaadata?
[Täisarv]
Kopra kodulinna tänavad moodustavad ruudustiku. Kobras ei mäleta, kuhu ta oma auto parkis, aga teab, et see on mingil ristmikul.
Auto leidmiseks liigub kobras ühelt ristmikult teisele põhja, lõuna, ida või lääne suunas. Iga kord, kui ta jõuab järgmisele ristmikule, ütleb äpp tema telefonis, mitme tänavavahe kaugusel ta oma autost on. Näiteks allolev joonis illustreerib olukorda, kus kobras on autost 6 tänavavahe kaugusel.
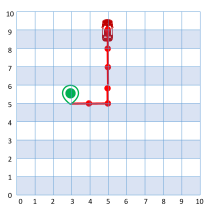
Igal ristmikul peab kobras valima, millises suunas edasi liikuda. Esimese suuna valib ta juhuslikult, edasi juhindub järgmistest reeglitest:
Siin on üks näide:
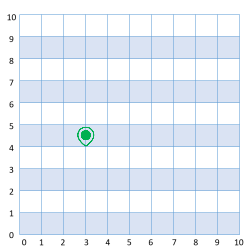 Lähtekoht Autoni 5 tänavavahet |
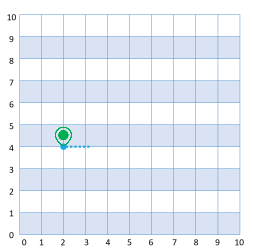 Valib juhuslikult läänesuuna Autoni 6 tänavavahet |
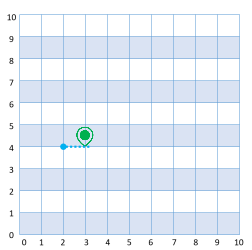 Läheb tagasi eelmisele ristmikule Autoni 5 tänavavahet |
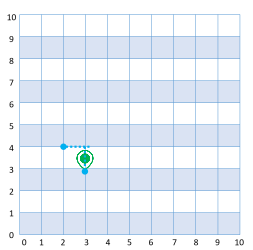 Võtab uue suuna lõunasse Autoni 6 tänavavahet |
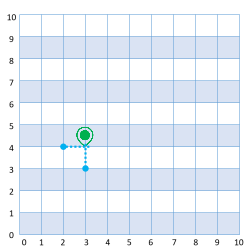 Läheb tagasi eelmisele ristmikule Autoni 5 tänavavahet |
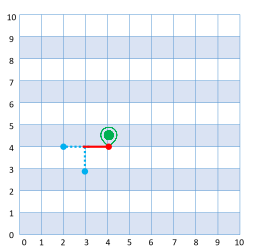 Võtab uue suuna itta Autoni 4 tänavavahet |
Ühel päeval oma autot otsides sai kobras järgmised signaalid (samm 0 on lähtekoht):
| Samm | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| Kaugus | 5 | 6 | 5 | 6 | 5 | 4 | 3 | 2 | 3 | 2 | 1 | 0 |
Milline järgmistest joonistest vastab kopra liikumistele?
[Raadionupud]
A.  B.
B. 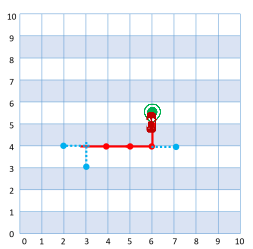 C.
C. 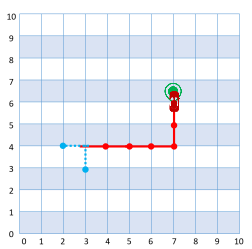 D.
D. 
Piraadikapten Krüger otsib peidetud aaret. Ta teab, et aare on ühes kaardil märgitud ruutudest.

Lisaks on tal ka maagiline seade, kuhu ta saab sisestada ükskõik millise hulga ruutude tähiseid, ja mis ütleb talle, kas aare on mõnes neist ruutudest. Näiteks, kui ta sisestab seadmesse "ACD" ja seade vastab "jah", siis tähendab see, et aare on ruudus A või ruudus C või ruudus D.
Milline on vähim arv sisestusi, mille Krüger peab tegema, et aarde asukoht teada saada?
[Täisarv]
Mimi ja Kimi kasutavad salajaste sõnumite vahetamiseks järgmist süsteemi:
Kõigepealt jagavad nad teksti kindla märkide arvuga lõikudeks. Kui viimane lõik tuleks teistest lühem, lisavad nad selle lõppu tühikuid. Näiteks, kui nad tahaks teksti "AMORE CUPID" jagada 3-märgilisteks lõikudeks, oleks tulemus "AMO", "RE ", "CUP", "ID ".
Seejärel muudavad nad märkide järjekorra igas lõigus vastupidiseks. Eelmist näidet jätkates oleks tulemus "OMA", " ER", "PUC", " DI".
Lõpuks valivad nad arvujada, mis näitab, millises järjekorras saadud lõigud kokku kleepida. Näiteks jada (3, 1, 4, 2) korral oleks tulemus "PUCOMA DI ER".
Üksteise sõnumite mõistmiseks peavad neil mõlemal olema teada lõikude pikkus ja nende kokkukleepimise järjekord. Selles näites olid need 3, (3, 1, 4, 2). Sellist infot nimetatakse salakirja võtmeks.
Võtme teatamiseks saadab Kimi iga päev esimese sõnumina "I LOVE YOU MIMI".
Milline on tänane võti, kui Mimi sai hommikul kodeeritud sõnumi "Y EV IMIM UOOL I"?
[Raadionupud]
A. 2, (4, 3, 8, 7, 5, 6, 1, 2)
B. 3, (3, 2, 5, 4, 1)
C. 4, (2, 4, 3, 1)
D. 5, (2, 3, 1)
Koprad ehitasid masina, mis teeb põrandale värvilisi mustreid. Materjalid lähevad masinasse sisse kuulides ja liiguvad torudes vastavalt masina lülitite olekutele. Kui kuul läheb lülitist läbi, keerab lüliti ennast vastupidisesse asendisse ja järgmine kuul läheb teise torusse.
Allolev joonis selgitab, kuidas esimene kuul läheb ise vasakule, aga pöörab lülitit nii, et teine kuul läheb paremale. Teine kuul läheb ise paremale, aga pöörab lüliti tagasi nii, et järgmine kuul läheks jälle vasakule.
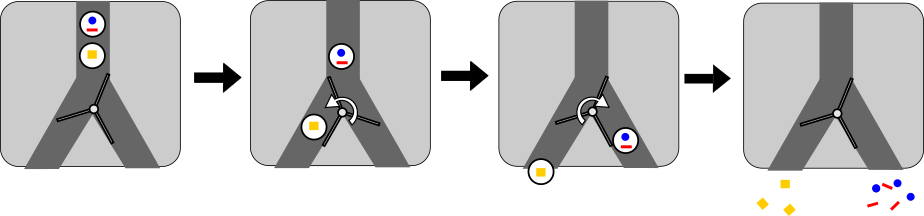
Iga kuuli peale on märgitud, millise mustri selle kuuli sisu põrandale teeb, kui see kuul maha kukub. Kui masina samast torust kukuvad välja mitu erinevat kuuli, siis nende mustrid segunevad. Kui samast torust kukuvad välja mitu ühesugust kuuli, siis teevad nad kõik ühesuguse mustri.
Nüüd tahavad koprad teha põrandale sellise mustri:
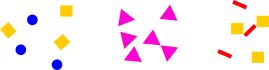
Millise kuulide jada peaks nad selleks allolevasse masinasse panema?
[Raadionupud]
A. 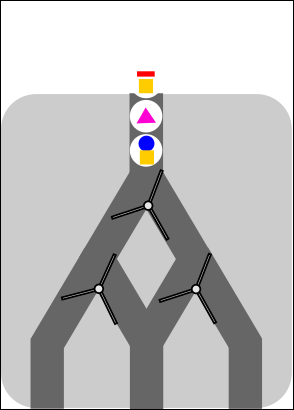 B.
B.  C.
C.  D.
D. 
Alice ja Bob mängivad äraarvamismängu. Laual on 10 doominokivi:

Bob valib ühe kivi, aga ei ütle, millise. Alice võib seejärel talle esitada jah/ei vastustega küsimusi, et ära arvata, millise kivi Bob valis.
Alice tahab esitada küsimusi nii, et Bobi iga vastus jagaks allesjäänud kivide hulga täpselt pooleks.
Millise järgmistest küsimustest peaks Alice esimesena esitama?
[Raadionupud]
A. Kas kivi kahel poolel kokku on vähemalt 7 silma?
B. Kas kivi suurema silmade arvuga poolel on vähemalt 4 silma?
C. Kas kivi väiksema silmade arvuga poolel on vähemalt 2 silma?
D. Kas kivi pooltel on sama arv silmi?
Joonistamisrobotil on kaks põhikäsku
F tähendab "liigu üks samm edasi";R tähendab "pööra kohapeal 90 kraadi paremale".Kõiki teisi tähti võib kasutada käsujadade nimedena. Näiteks
A = FFF määrab A tähenduseks "liigu kolm sammu edasi";B = ARA määrab B tähenduseks "tee A (ehk tee FFF), siis pööra kohapeal 90 kraadi paremale ja tee uuesti A".Roboti programmi alguses võib olla hulk selliseid käsujadade defineerimise ridu. Programmi viimane rida peab alati olema Draw käsk, mis lõpuks pildi valmis joonistab.
John püüab koostada programmi järgmise kujundi joonistamiseks, kus iga lõik on roboti ühe sammu pikkune:
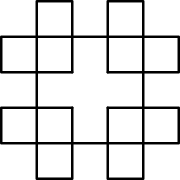
Selleks on John kirjutanud järgmise 5-realise programmi:
1 W = FF
2 X = RFR
3 Y = WXW
4 Z = YWYR
5 Draw ZZZZKahjuks on Johni programmis viga ja robot joonistab soovitust erineva kujundi.
Johni sõber Jack vaatas programmi ja andis Johnile vihje, et viga programmis on ühetäheline.
Mitmendal real viga on?
[Raadionupud]
A. Real 1
B. Real 2
C. Real 3
D. Real 4
E. Real 5
Koprapoe juhataja Frida pakub püsiklientidele hinnasoodustust. Tal on arvutustabel kõigi oma klientide selle nädala ostude infoga, kus veerus F tähendab 1 püsiklienti ja 0 tavaklienti:
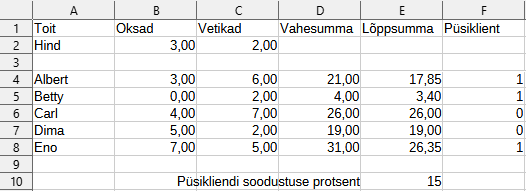
Milline valem peaks olema lahtris E4, et selle kopeerimisel lahtritesse E5 kuni E8 arvutaks tabel õigesti kõigi klientide lõppsummad?
Tabelarvutuse avaldise IF(T;A;B) väärtus on A, kui tingimus T kehtib, ja B, kui T ei kehti.
[Raadionupud]
A. =IF(F4=1;D4;D4*(1-E$10)/100)
B. =IF(F4=1;D4;D4*(1-E$10/100))
C. =IF(F4=1;D4*(1-E$10)/100;D4)
D. =IF(F4=1;D4*(1-E$10/100);D4)
Märt avastas hiljuti tobeda vea, mille ta tegi hästi pikas enda kirjutatud tekstis: igal pool, kus ta on kirjutanud "õieti", peaks olema "õigesti", ja igal pool, kus ta on kirjutanud "õigesti", peaks olema "õieti".
Õnneks on Märt päris tark! Tal on tekstitoimeti, millega ta saab asendada jada tähemärke teistsuguse jadaga.
Vaata, mis juhtub lausega, kui asendada kõik se-d dõ-dega!
Vaata, mis juhtub laudõga, kui adõndada kõik dõ-d dõ-dega!Või näiteks asendades kõik k-d r-dega.
Või näiters asendades rõir r-d r-dega.Mida Märt tegi, et oma tekst ära parandada?
Vihje: märki $ ta oma tekstis ei kasutanud!
[Raadionupud]
A. Asendas kõik "õieti"-d "õigesti"-tega ja siis kõik "õigesti"-d "õieti"-tega
B. Asendas kõik "õigesti"-d "õieti"-tega ja siis kõik "õieti"-d "õigesti"-tega
C. Asendas kõik "õigesti"-d $-tega, siis kõik "õieti"-d "õigesti"-tega ja siis kõik $-d "õieti"-tega
D. Asendas kõik "õieti"-d $-tega, siis kõik $-d "õigesti"-tega ja siis kõik "õigesti"-d "õieti"-tega
Aive värvib lihavõtteks valgeid kanamune. Värvimiseks paneb ta muna pöörlevale alusele ja hoiab pintslit selle vastas; nii saab ta kiiresti munale värvilise triibu.
Ühe värvimise ajal Aive pintslit ei liiguta, aga iga värvimise järel keerab ta muna ümber:

Mitut värvi üksteise peale kandes need segunevad ja moodustavad uusi värve:
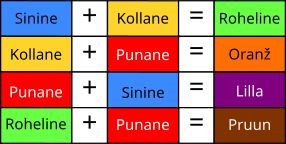
Ühe muna värvis Aive nii, nagu näidatud alloleval joonisel. Milline on tulemus?

[Raadionupud]
A.  B.
B.  C.
C. 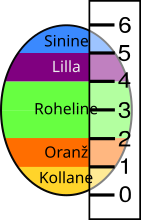 D.
D. 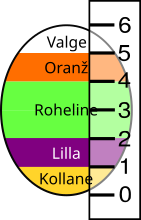
Superkobras on arvutimäng, mille taust koosneb varem ette valmistatud paneelidest. Programm lisab järjest uusi paneele ekraani paremasse serva ja eemaldab vanu paneele ekraani vasakust servast, luues nii liikumise illusiooni:

Uusi paneele valitakse vastavalt allolevale skeemile: vaadatakse, milline paneel on praegu ekraanil kõige parempoolsem ja siis valitakse järgmiseks paneeliks juhuslikult üks neist, mille peale sellest paneelist algavad nooled näitavad. Näiteks paneeli  järel võib tulla kas uuesti
järel võib tulla kas uuesti  või
või  .
.
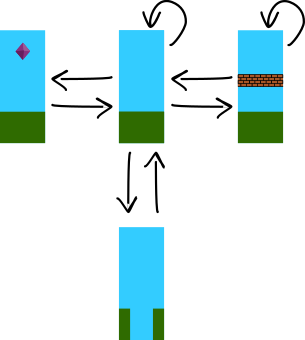
Milline järgmistest piltidest kindlasti EI SAA olla mängu Superkobras taust?
[Raadionupud]
A. 
B. 
C. 
D. 