

Kobras kaotas oma tuulelohe kõrgesse rohtu kasvanud põllule! Lohe pikk nöör läks sassi, mistõttu on raske lohe asukohta täpselt kindlaks teha.
Põld on jagatud 15 veeruks. Iga veeru saab eraldi läbi otsida, et näha, mitu korda lohe nöör seda läbib.
Kuidas lohe minimaalse arvu veergude läbi otsimisega üles leida?
[Interaktiivne]
(Klõpsa veergudel, kuni leiad lohe. Klõpsi veerge järjekorras, mis tagab lohe leidmise minimaalse arvu klõpsudega.)
(Selles ülesandes peidetakse lohe ülesannet otsast alustades iga kord erinevasse kohta.)
Kuna lohe peidetakse iga kord erinevasse kohta, ei saa selles ülesandes üht fikseeritud õiget vastust näidata, aga lohe saab alati leida ülimalt 4 klõpsuga.

Robot istutab peenrasse ritta lilli. Peenra igal kohal võib olla kas lill või silt või võib koht olla tühi.
Robot tegutseb järgmiste reeglite järgi:
Milline see peenar istutamise lõpuks välja näeb?

[Interaktiivne]
(Lohista lilled õigetesse kohtadesse.)
Õige vastus on:


Koprasaarel on 18 küla, nagu näha alloleval joonisel. Igas külas on hulk käskjalgu. Kui küla tahab teistele sõnumit saata või saab ise uue sõnumi, toimetavad käskjalad selle järgmisel päeval kõigile naaberküladele.
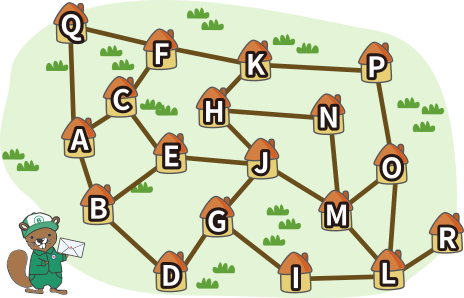
Näiteks kui küla A saadab sõnumi, kulub sellel küladesse B, C ja Q jõudmiseks 1 päev, küladesse D, E ja F jõudmiseks 2 päeva, ja nii edasi, kuni kõik külad on sõnumi kätte saanud.
Kui küla J saadab sõnumi, siis mitme päevaga see kõigi teiste küladeni jõuab?
[Täisarv]
Õige vastus on: 4 päevaga.

Ühes saarestikus on võimalik liikuda ühelt saarelt teisele, kui neil saartel on ühesugused võlumajad.
Näiteks saarelt A on võimalik liikuda saartele D ja E, kasutades valge uksega maju, ja saarele H, kasutades punase uksega maju:
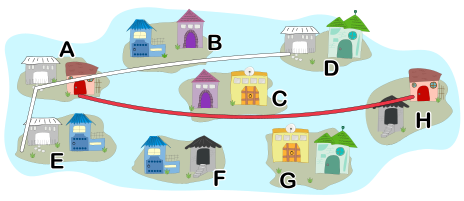
Noral on skeem, kus kõik kaheksa saart on tähistatud tähtedega. Skeemil olid jooned, mis tähistasid võlumajadega otseühendusi saarte vahel. Kahjuks on jooned skeemilt kustunud.
Aita Noral skeem taastada!
[Interaktiivne]
(Kahe saare ühendamiseks lohista hiirega ühelt teisele. Joone kustutamiseks klõpsa sellel.)
Õige vastus on:
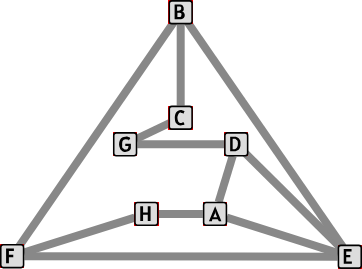

Kooli õpilasesindus läheb ühisele õhtusöögile. Kui kaks esinduse liiget on sõbrad, siis nad on õhtusöögil kõrvuti istudes rõõmsad, aga kui nad ei ole sõbrad, siis ei taha nad kõrvuti istuda.
Paiguta inimesed laua ümber toolidele. Kui paned kõrvuti kaks inimest, kes pole sõbrad, muutuvad nad kurvaks ja lähevad näost punaseks. Paiguta kõik inimesed nii, et nad oleks rõõmsad.
[Interaktiivne]
(Lohista näod A–F laua ümber toolidele.)
(Selles ülesandes on fikseeritud, kes on omavahel sõbrad ja kes mitte, aga tähised A–F jagatakse ülesannet otsast alustades iga kord erinevalt.)
Kuna tähised jagatakse iga kord erinevalt, ei saa selles ülesandes üht fikseeritud õiget vastust näidata.

Biberonid on ained, mille molekulid koosnevad elementidest A ja C. Kui lisada kasvõi üks tilk üht biberoni teisele, võib see teise biberoni koostise täiesti ära muuta.
Tulemuseks saadava biberoni koostise määravad lähtebiberonide koostised vastavalt järgmistele reeglitele:

Näiteks, kui lisada tilk biberoni ACC biberonile ACA, siis muutub biberon ACA biberoniks CCA:
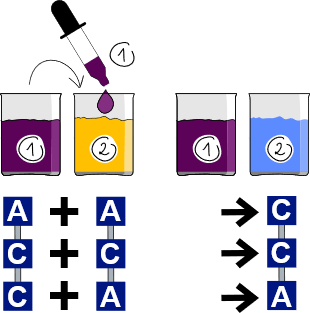
Meil on kolm anumat, 1, 2 ja 3, mis sisaldavad biberone CAC, ACA ja AAC. Me saame anda korraldusi lisada tilk biberoni ühest anumast (näiteks anumast 2) teise anumase (näiteks anumasse 3).
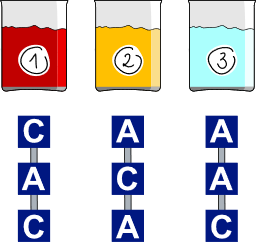
Vaheta anumate 1 ja 3 sisu: anumasse 1 on vaja saada biberon AAC, anumasse 2 peab jääma biberon ACA ja anumasse 3 on vaja saada biberon CAC.
[Interaktiivne]
(Lohista vajalikud korraldused kollastesse kastidesse. Iga korraldust võib kasutada korduvalt.)
Võimalikud õiged vastused on:
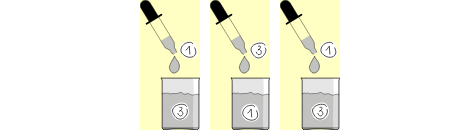
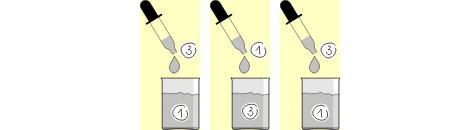

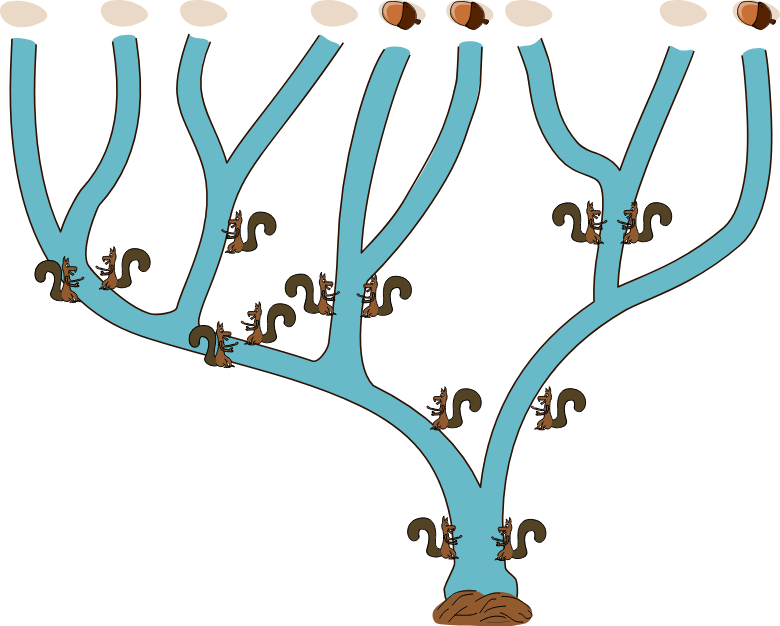
Kobras mängib oravatega tõrude püüdmise mängu. Selles mängus on üheksa oja, mis kõik jõuavad lõpuks kopra tammi juurde.
Kopral on kolm tammetõru ja ta võib igaühe neist erinevast ojast allavoolu lasta.
Oravad valvavad ojade ääres ühe- või kahekaupa:

|
Üksik orav:
|

|
Kaks oravat:
|
Millistesse ojadesse peaks kobras tõrud panema, et vähemalt üks neist jõuaks tammi juurde kohale?
[Interaktiivne]
(Lohista tõrud õigetesse ojadesse.)
Õige vastus on:

Saral on mustadest ja valgetest ruutudest koosnev rida.
Ta tahab rea kirjelduse esitada järgmiste reeglite alusel:
Mõned näited nende reeglite rakendamisest 8 ruudust koosnevatele ridadele:
| Rida | Kirjeldus |
|---|---|
 |
W |
 |
XWB |
 |
XXBWB |
 |
XBXWXBW |
Milline on järgmise rea kirjeldus?

[Tekstikast]
Õige vastus on: XXXWBWXBXBW.

Robi koostas rannaliivale erinevatest kujunditest ilusa mosaiigi.
Tema kasutatud kujundid on kas helesinist või tumehalli värvi ja igal kujundil on 3, 4, 5 või 6 väljaulatuvat nurka.
Robi pani tähele, et tema mosaiigis on igas reas ja igas veerus:
Siis tuli aga suurem laine ja asendas Robi mosaiigis kaks kujundit uutega. Nüüd on mosaiik selline:

Rannal veel viis kujundit, milleks kaks olid enne Robi mosaiigis. Kahjuks Robi ei mäleta, millised need olid!
Millised kaks järgmistest kujunditest olid Robi esialgses mosaiigis?
(Märgi täpselt kaks varianti.)
[Märkeruudud]
A.  B.
B.  C.
C.  D.
D.  E.
E. 
Õige vastus on: A, C.

Anna, Bert ja Corry mängivad mängu kivi-paber-käärid uut varianti.
Tuletame meelde reeglid:
Mängu alguses istuvad mängijad toolidel ja igaüks hoiab oma kaarti kõigile nähtavalt:

Edasi teevad nad vahetusi. Iga vahetus tähendab, et kaks kobrast vahetavad omavahel oma kaardid.
Berti ainus eesmärk on Corryt võita. Milline järgnevatest strateegiatest selle garanteerib?
[Raadionupud]
A. Bert peab hoolitsema, et tema ja Corry teeks omavahel paaritu arvu vahetusi.
B. Ükskõik kui palju vahetusi kokku tehakse, ei tohi Bert kunagi teha vahetust Corryga.
C. Ükskõik kui palju vahetusi kokku tehakse, peab Bert kõik oma vahetused tegema Corryga.
D. Bert peab hoolitsema, et kokku tehtaks paarisarv vahetusi.
Õige vastus on: D.

Arvutigraafikas kasutatakse loogikatehteid kujundite vahel, et lihtsamatest kujunditest keerulisemaid koostada.
Allpool on mõned põhitehete AND, OR ja NOT näited:
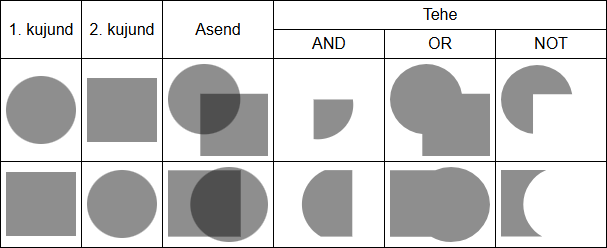
Neid tehteid üksteise järel rakendades võime saada järjest keerulisemaid kujundeid:
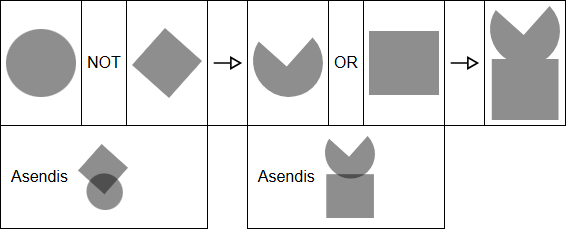
Nüüd on sul neli kujundit ja kolm etteantud tehet, et saada tulemuseks noole järel olev kujund.
[Interaktiivne]
(Lohista sinised kujundid õigetesse kohtadesse.)
Võimalikud õiged vastused on:



Ben peab koprakülas poodi. Tal on laoseisu andmed arvutustabelis ja parema ülevaate saamiseks kasutab ta tingimuslikku vormingut:
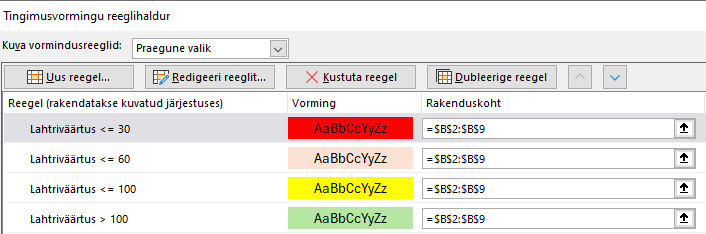
Näiteks, kui mõnda kaupa on laos rohkem kui 100 tükki, on selle lahtri taust tabelis roheline.
Eileõhtuse seisuga oli Beni laoseis järgmine:
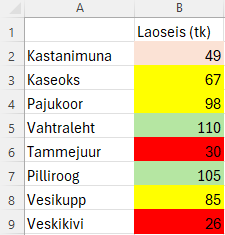
Täna hommikul tuli lattu juurde 3 pajukoort, 15 vesikuppu ja 4 veskikivi.
Päeva jooksul müüs Ben ainult 7 kaseoksa.
Milliste lahtrite värvid tänase päeva andmete tabelisse sisestamisel muutusid?
(Märgi kõik õiged vastused.)
[Märkeruudud]
A. Kastanimuna
B. Kaseoks
C. Pajukoor
D. Vahtraleht
E. Tammejuur
F. Pilliroog
G. Vesikupp
H. Veskikivi
Õige vastus on: B, C.

Paljudes programmides on võimalik andmete otsimisel kasutada mustreid.
Üks levinud süsteem otsitavate tekstimustrite kirjeldamiseks on järgmine:
? vastab mistahes üks märk tekstis.* vastab mistahes (sealhulgas ka nullist märgist koosnev) märgijada tekstis.Näiteks otsingusõnale X*X vastavad nii XYX kui XYYX, aga otsingusõnale X?X vastab neist kahest ainult esimene.
Mõnikord aga pole üheselt määratud, milline tekstiosa igale otsingusõna märgile vastab.
Näiteks võib tekst XYX vastata otsingusõnale X**X kahel erineval viisil:
| Otsingusõna märk | X |
* |
* |
X |
|---|---|---|---|---|
| Teksti vaste 1 | X |
Y |
X |
|
| Teksti vaste 2 | X |
Y |
X |
Mitmel erineval viisil võib tekst ABCDA vastata otsingusõnale A**?*A?
[Täisarv]
Õige vastus on: 6.

Momole meeldib robotitega labürindimängu mängida. Selles mängus on laual hulk takistusi  ja Momo peab juhtima robotid
ja Momo peab juhtima robotid  sihtmärgile
sihtmärgile  .
.
Momo saab roboteid juhtida lihtsa programmiga. Robotid täidavad programmis olevaid käske järjest. Programmis võib kasutada järgmisi käske:
Nüüd on ühes labürindis kolm robotit. Momo peab koostama programmi, mille järgi tegutsedes jõuaks kõik kolm robotit sihtmärgile. Robotid alustavad erinevatest kohtadest ja erinevatesse suundadesse pööratult, aga peavad kõik jõudma samale sihtmärgile.
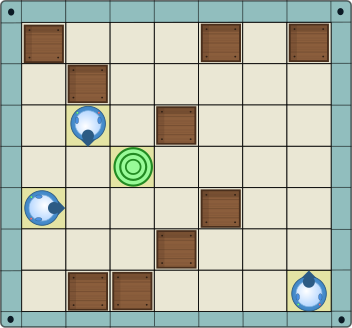
Aita Momol koostada võimalikult lühike programm, mis kõik robotid sihtmärgile juhib. Võid eeldada, et robotid ei põrka kunagi omavahel kokku.
[Interaktiivne]
(Lohista vajalikud käsud õigesse järjekorda programmiks.)
Õige vastus on:


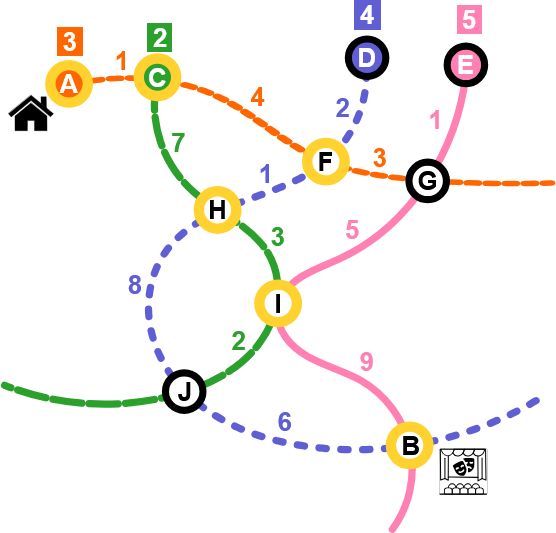
Markuse kodulinnas on neli ühesuunalist bussiliini. Alloleval joonisel on bussipeatused märgitud mustade ringidega ja liinid värviliste joontega. Värvilise taustaga peatused on bussiliinide alguspunktid.
Kõigi liinide esimesed bussid väljuvad samal ajal. Järgmised bussid väljuvad erinevate intervallidega. Iga liini intervall on märgitud selle liini alguspeatuse juures värvilises ristkülikus. Näiteks oranži liini interval on 3 minutit: bussid väljuvad peatusest A minutitel 0, 3, 6, 9...
Arvud bussiliinide lõikude juures näitavad peatuste vahelist sõiduaega (minutites). Peatustes peatumine ning reisijate maha ja peale minek aega ei võta.
Mitme liini lõikumiskohas olevates peatustes saab ümber istuda. Kui Markus jõuab ühe bussiga peatusse, saab ta ümber istuda teisele bussile, mis jõuab sinna peatusse kas täpselt samal ajal või hiljem.
Milliste peatuste kaudu saab Markus kõige kiiremini oma kodust (peatus A) teatrisse (peatus B)?
[Interaktiivne]
(Märgi kõik peatused, mida Markus läbib (A ja B kaasa arvatud). Peatuse märkimiseks klõpsa sellel. Tühistamiseks klõpsa uuesti.)
Õige vastus on:
Copyright © 2025 Bebras – International Challenge on Informatics and Computational Thinking.
Licensed under Creative Commons Attribution-ShareAlike 4.0 International License.
Flag icons by GoSquared.