

Бобр потерял своего воздушного змея в поле с высокой травой! Длинная веревка змея запуталась, и теперь сложно определить точное местонахождение змея.
Поле разделено на 15 столбцов. Каждый столбец можно просмотреть отдельно, чтобы узнать, сколько раз веревка воздушного змея пересекает этот столбец.
Как найти воздушного змея, просмотрев минимальное количество столбцов?
[Interaktiivne]
(Щёлкай на столбцы до тех пор, пока не найдёшь воздушного змея. Щёлкай на столбцы в порядке, позволяющем найти воздушного змея за минимальное количество щелчков.)
(Обрати внимание, что, каждый раз начиная задание с начала, воздушный змей прячется в разных местах.)
Поскольку каждый раз воздушный змей прячется в разных местах, то в этом задании нет одного фиксированного правильного ответа, но воздушного змея всегда можно найти всего за 4 щелчка.

Робот высаживает на клумбе цветочный ряд. Каждое место на клумбе может быть с цветком или с табличкой, или же быть пустым.
Робот действует по следующим правилам:
Как будет выглядеть эта клумба в конце посадки?

[Interaktiivne]
(Перетащи цветы в правильные места.)
Правильный ответ:


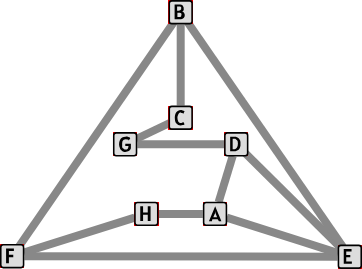
На Бобровом острове расположено 18 деревень, как показано на нижеприведённом рисунке. В каждой деревне есть несколько гонцов. Если деревня хочет отправить сообщение другим или сама получает новое сообщение, то на следующий день гонцы доставляют его во все соседние деревни.

Например, если деревня A отправляет сообщение, то оно дойдёт до деревень B, C и Q за 1 день, до деревень D, E и F — за 2 дня, и так далее, пока сообщение не будет доставлено всем деревням.
Если деревня J отправит сообщение, то за сколько дней оно достигнет всех остальных деревень?
[Täisarv]
Правильный ответ: за 4 дня.

В пределах одного архипелага с одного острова на другой можно перемещаться, если на этих островах есть одинаковые волшебные дома.
Например, с острова A можно попасть на острова D и E, используя дома с белыми дверьми, а на остров H при помощи домов с красными дверьми:

У Наташи есть схема, где все восемь островов отмечены буквами. На схеме были линии, обозначающие прямые соединения между островами с помощью волшебных домов. К сожалению, линии были удалены со схемы.
Помоги Наташе восстановить схему!
[Interaktiivne]
(Перетащи мышь с одного острова на другой, чтобы соединить два острова. Щёлкни на линию, чтобы её удалить.)
Правильный ответ:

Члены ученического совета пришли на ужин. Если два члена совета являются друзьями, то на ужине они с удовольствием сидят рядом, но если они не друзья, то они не хотят сидеть рядом друг с другом.
Рассади людей на стулья вокруг стола. Если посадишь рядом двух человек, которые не являются друзьями, то они расстроятся и покраснеют. Рассади всех так, чтобы все были счастливы.
[Interaktiivne]
(Перетащи обозначенные буквами A–F лица на стулья вокруг стола.)
(В этом задании зафиксировано, кто с кем дружит, а кто нет. Однако, каждый раз начиная задание с начала, буквы A–F назначаются по-разному.)
Поскольку каждый раз буквы назначаются по-разному, то в этом задании нельзя показать одного фиксированного правильного ответа.

Бибероны — это вещества, молекулы которых состоят из элементов А и С. Если добавить хотя бы одну каплю одного биберона к другому, это может полностью изменить состав второго биберона.
Состав полученного биберона определяется составом исходных биберонов в соответствии со следующими правилами:

Например, если каплю биберона ACC добавить к биберону ACA, то биберон ACA превратиться в биберон CCA:

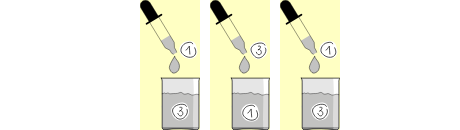
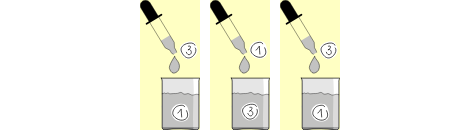
У нас есть три пробирки, 1, 2 и 3, в которых находятся бибероны CAC, ACA и AAC. Мы можем дать указание добавить каплю биберона из одной пробирки (например, из пробирки 2) в другую пробирку (например, в пробирку 3).

Поменяй местами содержимое пробирок 1 и 3: в пробирке 1 должен получить биберон AAC, в пробирке 2 должен остаться биберон ACA, а в пробирке 3 должен получить биберон CAC.
[Interaktiivne]
(Перетащи в жёлтые квадратики необходимые указания. Каждое указание может быть использовано повторно.)
Возможные правильные ответы:

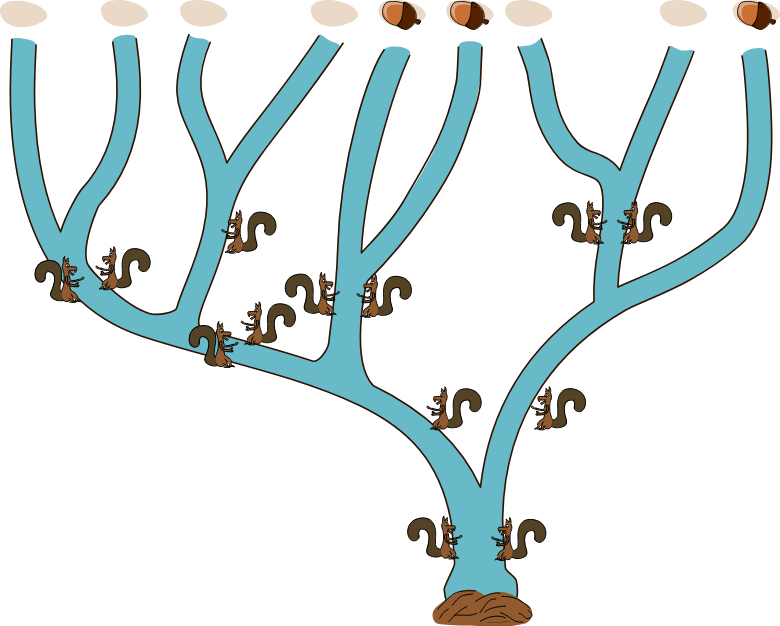
Бобр играет с белками в игру по ловле желудей. В этой игре используется девять ручьёв, каждый из которых в итоге доходит до плотины бобра.
У бобра есть три жёлудя, которые он должен спускать вниз по течению по разным ручьям.
Белки дежурят вдоль ручьёв по одной или по две:

|
Одна белка:
|

|
Две белки:
|
В какие ручьи бобру следует бросить жёлуди, чтобы хотя бы один из них достиг плотины?
[Interaktiivne]
(Перетащи жёлуди к правильным ручьям.)
Правильный ответ:

У Саши состоящий из чёрных и белых квадратов ряд.
Он хочет представить описание ряда, используя следующие правила:
Ниже приведены некоторые примеры применения этих правил к рядам, состоящим из 8 квадратов:
| Ряд | Описание |
|---|---|
 |
W |
 |
XWB |
 |
XXBWB |
 |
XBXWXBW |
Каково описание следующего ряда?

[Tekstikast]
Правильный ответ: XXXWBWXBXBW.

На пляже Робин создал красивую мозаику из разных фигур.
Используемые фигуры были либо светло-голубые, либо темно-серые, и каждая фигура имела 3, 4, 5 или 6 выступающих углов.
Робин обратил внимание, что в его мозаике в каждом ряду и в каждом столбце:
Но вдруг пришла большая волна и заменила в мозаике Робина две фигуры на новые. Теперь мозаика выглядит так:

На пляже есть ещё пять фигур, две из которых ранее были использованы в мозаике Робина. К сожалению, Робин не помнит, что это были за фигуры!
Какие две из следующих фигур были в первоначальной мозаике Робина?
(Выбери ровно два варианта.)
[Märkeruudud]
A.  B.
B.  C.
C.  D.
D.  E.
E. 
Правильный ответ: A, C.

Анна, Боря и Вася играют новую версию игры камень-ножницы-бумага.
Напомним правила:
В начале игры игроки сидят на стульях, и каждый держит свою карту так, чтобы другие её видели:

Затем они делают обмены. Каждый обмен означает, что два бобра обмениваются друг с другом своими картами.
Единственная цель Бори — победить Васю. Какая из следующих стратегий гарантирует ему эту победу?
[Raadionupud]
A. Боря должен позаботиться о том, чтобы он и Вася сделали нечётное количество обменов.
B. Независимо от того, сколько всего обменов будет сделано, Боря никогда не должен делать обмен с Васей.
C. Независимо от того, сколько всего обменов будет сделано, Боря должен все свои обмены сделать с Васей.
D. Боря должен позаботиться о том, чтобы общее число обменов было чётным.
Правильный ответ: D.

В компьютерной графике к фигурам применяются логические операции, чтобы из более простых фигур создать более сложные.
Ниже приведены некоторые примеры с основными операциями AND, OR и NOT:

Применяя эти операции одну за другой, мы можем получать все более сложные фигуры:

Теперь у тебя есть четыре фигуры и три заданных операции, чтобы получить расположенную после стрелки фигуру.
[Interaktiivne]
(Перетащи синие фигуры в правильные места.)
Возможные правильные ответы:



Бен управляет магазином в деревне бобров.
Он заносит данные о складских запасах в электронную таблицу, и для лучшего обзора данных использует условное форматирование:

Например, если на складе имеется более 100 единиц какого-то товара, то в таблице фон этой ячейки будет зелёным.
По состоянию на вчерашний вечер складские запасы Бена были следующими:

Сегодня утром на склад прислали 3 коры ивы, 15 водяных лилий и 4 камня.
В течение дня Бен продал только 7 веток берёзы.
Цвета каких ячеек изменились при занесении сегодняшних данных в таблицу?
(Отметь все правильные ответы.)
[Märkeruudud]
A. Каштан
B. Ветка берёзы
C. Кора ивы
D. Лист клёна
E. Корень дуба
F. Тростник
G. Водяная лилия
H. Камень
Правильный ответ: B, C.

Во многих программах для поиска данных можно использовать шаблоны.
Одна из распространённых систем для описания поисковых текстовых шаблонов выглядит следующим образом:
? соответствует в тексте один любой знак.* соответствует в тексте любая последовательность знаков (включая и ту, что не содержит ни одного знака).Например, поисковому слову X*X соответствует как XYX, так и XYYX, но поисковому слову X?X соответствует только первый из этих двух.
Однако иногда остается неясно, какая часть текста соответствует каждому знаку в поисковом слове.
Например, текст XYX может соответствовать поисковому слову X**X двумя разными способами:
| Знак поискового слова | X |
* |
* |
X |
|---|---|---|---|---|
| Совпадение текста 1 | X |
Y |
X |
|
| Совпадение текста 2 | X |
Y |
X |
Сколькими способами текст ABCDA может соответствовать поисковому слову A**?*A?
[Täisarv]
Правильный ответ: 6.

Момо любит играть в лабиринт с роботами. В этой игре на игровом поле встречается множество препятствий  , и Момо должен направить роботов
, и Момо должен направить роботов  к цели
к цели  .
.
Момо может управлять роботами с помощью простой программы. Роботы последовательно выполняют команды программы. В программе можно использовать следующие команды:
Теперь в одном лабиринте одновременно находятся три робота. Момо должен написать программу, которая, если ей следовать, приведёт всех трёх роботов к цели. Роботы стартуют из разных мест и смотрят в разные стороны, но они все должны достичь одной и той же цели.

Помоги Момо написать самую короткую программу, которая позволит всем роботам достичь цели. Мы можем считать, что роботы никогда не сталкиваются друг с другом.
[Interaktiivne]
(Перетащи необходимые команды программы в правильном порядке.)
Правильный ответ:


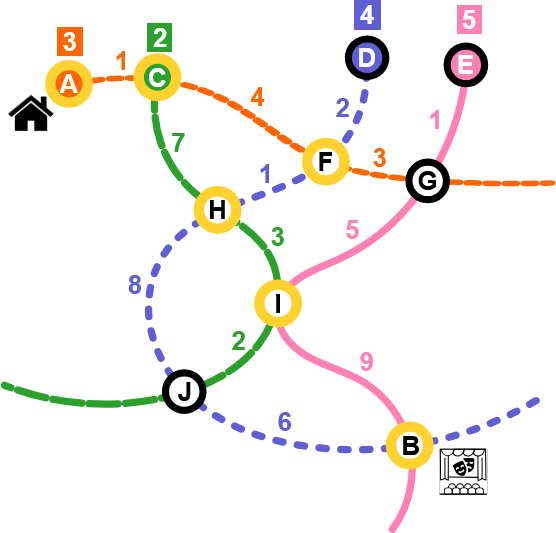
В родном городе Маркуса действуют четыре односторонних автобусных маршрута. На нижеприведённой схеме автобусные остановки обозначены чёрными кругами, а маршруты — цветными линиями. Остановки с цветным фоном — это начальные пункты отправки автобусных маршрутов.
Первые автобусы всех маршрутов отправляются одновременно. Последующие автобусы отправляются с разным интервалом. Интервалы движения автобусов на каждой линии указаны на начальных остановках этих линии в цветных квадратах. Например, интервал оранжевой линии составляет 3 минуты: автобусы отправляются с остановки A в 0, 3, 6, 9 минут...
Числа рядом с участками маршрута автобуса указывают время в пути между остановками (в минутах). Стоянка на остановках, а также посадка и высадка пассажиров не занимают времени.
На остановках, где пересекаются несколько линий, можно совершить пересадки. Когда Маркус прибывает на остановку на одном автобусе, он может пересесть на другой автобус, который прибудет на эту же остановку либо в то же самое время, либо позже.
Какие остановки позволят Маркусу быстрее всего добраться от дома (остановка A) до театра (остановка B)?
[Interaktiivne]
(Отметь все остановки, через которые проезжает Маркус (включая A и B). Щёлкни на остановку, чтобы отметить её. Щёлкни ещё раз, чтобы отменить выбор.)
Правильный ответ:
Copyright © 2025 Bebras – International Challenge on Informatics and Computational Thinking.
Licensed under Creative Commons Attribution-ShareAlike 4.0 International License.
Flag icons by GoSquared.