1. Imeline masin

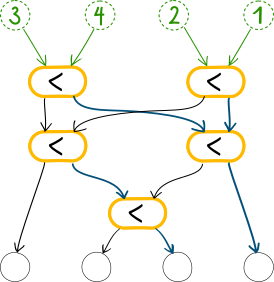
Kobrastel on imeline masin.

Sellesse pannakse ülevalt sisse neli arvu, näiteks 3, 4, 2 ja 1.

Edasi liiguvad arvud mööda nooli ja läbi lülide allapoole, kuni jõuavad kõige all olevatesse väljundpesadesse.

Iga lüli võrdleb kaht sissetulevat arvu ning suunab väiksema arvu edasi vasakpoolse ja suurema parempoolse noole suunas.

Siin on üks näide:

Küsimus

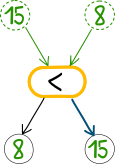
Mida see masin teeb?

[Raadionupud]

A. Väljastab arvud vastupidises järjekorras (tulemus on 1, 2, 4, 3).

B. Väljastab arvud kasvavas järjekorras (tulemus on 1, 2, 3, 4).

C. Väljastab arvud kahanevas järjekorras (tulemus on 4, 3, 2, 1).

D. Väljastab arvud esialgses järjekorras (tulemus on 3, 4, 2, 1).

2. Parkimine

Tiinal on sünnipäev ja ta kutsus sõbrad külla. Sõbrad tulevad koos vanematega, kes pargivad oma autod maja ette.

Tiina maja ees on autode parkimiseks kolm rida. Igasse ritta mahub kolm autot. Iga auto valib saabudes ühe rea ja pargib sellele reale tänavast nii kaugele kui võimalik.

Kolm autot on juba parkinud nii, nagu allpool näha, ja see tähendab, et

• A pidi saabuma enne kui C;
• C peab lahkuma enne kui A.

Tiina sõbrad saabuvad sellises järjekorras: A, B, C, D, E, F, G, H, J.

Peo lõpus lahkuvad nad sellises järjekorras: G, D, F, J, H, C, B, A, E.

Küsimus

Kuidas peaks ülejäänud autod parkima, et ükski auto ei takistaks ühegi teise auto saabumist ega lahkumist?

[Interaktiivne]

(Lohista kõik autod sobivatele parkimiskohtadele.)

3. LED-keks

Koprad mängivad LED-keksu. Mänguväli koosneb kolme liiki ruutudest.

: Siniselt ruudult peab mängija hüppama näidatud arvu ruute paremale. Pärast seda muutub ruut ise punaseks.

: Punaselt ruudult peab mängija hüppama näidatud arvu ruute vasakule. Pärast seda muutub ruut ise siniseks.

: Musta ruudu võib mängija enne liikuma hakkamist muuta siniseks või punaseks.

• Kui mängija muudab ruudu alguses siniseks, peab ta sellele sattudes hüppama näidatud arvu ruute paremale ja ruut muutub pärast seda punaseks.
• Kui mängija muudab ruudu alguses punaseks, peab ta sellele sattudes hüppama näidatud arvu ruute vasakule ja ruut muutub pärast seda siniseks.

Mängija alustab alati kõige vasakpoolsemalt ruudult ja eesmärk on jõuda lõpuruudule vähima arvu hüpetega.

Mängija kaotab, kui ta

• ei jõua lõpuruudule;
• hüppab ruudustikust välja;
• hüppab mustale ruudule, mida ta alguses siniseks või punaseks muutnud ei ole.

Küsimus

Kuidas peaks Leena alloleval mänguväljal mustade ruutude värvid valima, et jõuda lõpuruudule vähima arvu hüpetega?

[Interaktiivne]

(Ruudu värvi muutmiseks kliki sellel. Muuta saab ainult neid ruute, mis on alguses mustad.)

4. Udune ilm

Kopramaa kaardi võib jagada ruutudeks.

Alguses on udu ainult mõnedes kaardiruutudes, aga iga tunniga levib see edasi naaberruutudesse nelja põhiilmakaare suunas: 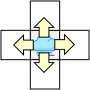, välja arvatud mägedega ruutudesse, kus ei ole kunagi udu.

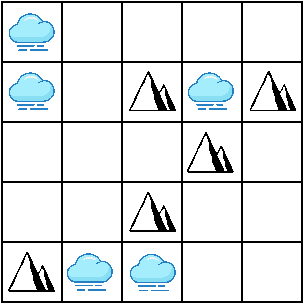
Üks näide:

Algseis	1 tunni pärast	2 tunni pärast

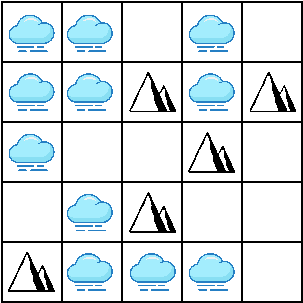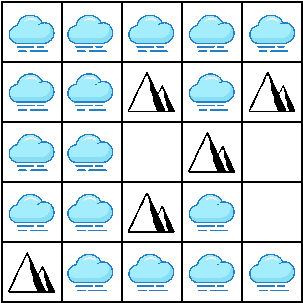Vaatame nüüd sellist kaarti:

Küsimus

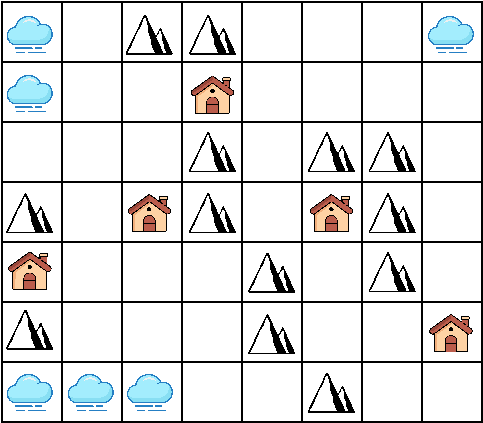
Mitme tunni pärast on udu kõigis majadega ruutudes?

[Täisarv]

5. Alati paremale

Robot Robi on rikkis ja peab sõitma garaaži remonti. Oma rikke tõttu liigub Robi järgmiselt:

• kui on võimalik, keerab ta alati paremale;
• kui paremale keerata ei saa, sõidab ta otse;
• vasakule keerata ei saa ta mingil juhul.

Aita Robil garaaži jõuda! Selleks pead sa panema seinad ette kõigisse neisse kohtadesse, kus paremale keeramine Robi valele teele viiks.

Küsimus

Joonisel on üks sein juba paika pandud. Mis on vähim arv seinu, mis on vaja veel juurde panna, et Robi garaaži jõuaks?

[Täisarv]

6. Automaatköök

Automaatköök oskab antud retseptide järgi valmistada mitut erinevat rooga:

Iga roa valmistamiseks peavad masinasse tulema täpselt õiged lähteained täpselt õiges järjekorras.

Roa valmistamisel kuluvad kõik selle lähteained ära ja nende asemel tuleb masina teisest otsast välja neist valmistatud roog. Masin ei saa ühe roa valmistamise ajal lähteaineid vahele jätta.

Masin võib kahe roa vahel mõne lähteaine vahele jätta. Siis tuleb see lähteaine masina teisest otsast muutmata kujul välja.

Näide:

Lähteained
võib masin jagada retseptideks
ja siis tuleb masinast välja 3 ühikut

Nüüd lähevad masinasse sellised lähteained:

Küsimus

Mis on vähim arv ühikuid, mis võib masinast välja tulla?

[Täisarv]

7. Pagarid

Koprad Albert ja Mario peavad oma pagaritöökotta veskist jahu tooma.

Albert jõuab korraga kanda 13 kg jahu ning tal kulub üks tund, et minna töökojast veskisse ja tulla jahuga tagasi. Mario jõuab kanda ainult 5 kg jahu, aga ta käib edasi-tagasi kõigest 30 minutiga.

Nad ei või mõlemad korraga veskile minna; alati peab vähemalt üks neist olema töökojas, et kliente vastu võtta.

Kui üks kobras on kolm korda järjest veskil käinud, peab ta vähemalt 30 minutit puhkama. Sel ajal ei saa ta jahu tassida, aga võib töökojas kliente vastu võtta.

Koprad tahavad 8-tunnise tööpäevaga tuua veskilt nii palju jahu kui võimalik.

Küsimus

Milline järgmistest väidetest on õige?

[Raadionupud]

A. Esimese veskil käigu peab tegema Albert.

B. Esimese veskil käigu peab tegema Mario.

C. Viimase veskil käigu peab tegema Mario.

D. Albert ei saa teha viimast veskil käiku.

E. Mario peab veskil käima ühe korra.

8. Kosmiline sõnum

Tim sai kosmosest sõnumi! Sõnum sisaldab tähestiku kirjeldust ja teadet.

Kahjuks on kosmiline kiirgus tähestiku kirjelduse osaliselt kustutanud. Aga õnneks on tähestikus kindel süsteem:

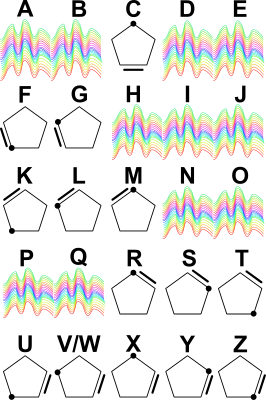
Sõnumi teate osa on selline:

Küsimus

Mis on teates kirjas?

[Tekstikast]

9. Lehesadu

Torm puhus meie otsustuspuult suurema osa lehti maha, ainult üks on veel alles!

Otsustuspuu kasutamine käib nii:

• võta vili ja vasta selle kohta otsustuspuu juures olevale küsimusele;
• liigu edasi vastavalt "jah" või "ei" noole suunas ja vasta noole otsas olevale küsimusele;
• jätka vastamist ja liikumist, kuni jõuad otsustuspuu leheni;
• lehes on kirjas, mis viljaga on tegu.

Enne tormi aitas otsustuspuu õigesti tuvastada kõik järgmised viljad:

Seemnete arv	Koore värv	Koor söödav?	Otsus
391	roheline	ei	arbuus
5	kollane	jah	õun
9	oranž	ei	apelsin
0	kollane	ei	banaan
5	punane	jah	õun
0	roheline	jah	viinamari
206	punane	jah	maasikas
6	roheline	jah	õun
10	oranž	ei	apelsin
173	punane	jah	maasikas

Küsimus

Pane otsustuspuu lehed tagasi õigetesse kohtadesse.

[Interaktiivne]

(Lohista kõik puu all olevad lehed õigetele kohtadele.)

10. Ümber laua

Neli kobrast istuvad ümber laua ja söövad igaüks erinevat toitu.

Me teame nende kohta järgmist:

• Bruno istub Davidist vasakul.
• Kobras, kes istub Clarast paremal, sööb praetud juuri.
• Anita sööb röstitud raage.
• Kobras, kes istub Anitast paremal, sööb keedetud puukoort.

Küsimus

Kus iga kobras istub ja mida iga kobras sööb?

[Interaktiivne]

(Lohista kõik koprad õigetele kohtadele laua ümber ja toidud õigetele kohtadele laua peal.)

11. Pildi teisendused

Xavier programmeerib oma esimest arvutimängu. Selleks õpib ta tundma piltide teisendamist.

Esialgu piirdub ta ainult kaht liiki teisendustega:

Algne pilt	Teisendus	Tulemus
	M (Peegelda vertikaaltelje suhtes)
	R (Pööra 90 kraadi päripäeva)

Nüüd tahab Xavier saada pildist pildi

Küsimus

Milline järgnevatest teisenduste jadadest seda ei saavuta?

[Raadionupud]

A. M, R

B. R, R, R, M

C. R, M

D. M, R, M, R, M, R

12. Häkaton

Häkatonid on Kopramaal populaarsed ja eelvoorudes osaleb sadu võistkondi. Žüriid hindavad iga projekti 10-palli süsteemis nelja kriteeriumi alusel: idee uudsus, teostuse praktilisus, prototüübi küpsus, esitlus.

Et vältida vigu finaali kutsumises, otsustas peakohtunik selle automatiseerida. Ta sisestas kõik hinded suurde tabelisse, kirjutas selle lahtrisse F2 valemi
     =IF(OR(AND(B2>=7;C2>=7);SUM(B2:E2)>30);"jah";"ei")
ja kopeeris selle valemi alla kogu veeru F ulatuses.

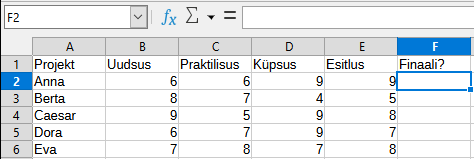
Selgituseks valemis kasutatud funktsioonide kohta:

• IF(tingimus;väärtus1;väärtus2) kui tingimus kehtib, on tulemus väärtus1; kui tingimus ei kehti, on tulemus väärtus2;
• OR(tingimus1;tingimus2) kehtib, kui kehtib kas tingimus1 või tingimus2 või mõlemad;
• AND(tingimus1;tingimus2) kehtib, kui tingimus1 ja tingimus2 mõlemad kehtivad;
• SUM(lahter1;lahter2) liidab kokku kõik arvud ristkülikus, mille vasak ülemine nurk on lahter1 ja parem alumine nurk lahter2 (lahter1 ja lahter2 kaasa arvatud).

Küsimus

Millised ekraanipildil näha olevast viiest võistkonnast kutsutakse finaali?

(Märgi kõik õiged vastused.)

[Märkeruudud]

A. Anna

B. Berta

C. Caesar

D. Dora

E. Eva

13. Sisukord

Bioloogiatunniks teeb Kaarel referaati lindudest ja loomadest. Referaadi sisukorda ei tee ta käsitsi, vaid laseb selle genereerida tekstitöötlusprogrammil.

Selleks märgib ta imetajate ja lindude peatükkide pealkirjad laadiga Pealkiri 1 (ingl Heading 1). Töös vaadeldud imetajate (rebane, hunt, jänes, kobras) jaotiste pealkirjad märgib ta laadiga Pealkiri 2 (ingl Heading 2). Kobraste jaotises on kaks alamjaotist, mis on ka sisukorras kajastatud.

Küsimus

Täna lisas Kaarel referaati jäneste jaotisse alamjaotised valgejänesest, halljänesest ja ameerika jänesest.

Kuidas peaks nende pealkirjad vormistama, et nad sisukorras õigesti kajastuksid?

[Raadionupud]

A. Need peaks märkima laadiga Pealkiri 1

B. Need peaks märkima laadiga Pealkiri 2

C. Need peaks märkima laadiga Pealkiri 3

D. Need peaks märkima laadiga Pealkiri 4

14. Sugupuu

Annika ja Daniel on suguvõsa kokkutulekul. Seal küsitakse neilt: "Kuidas te omavahel suguluses olete?"

Annika võtab tüki paberit ja visandab sugupuu. Tema joonisel kannavad emased koprad lehve ja isased mütse:

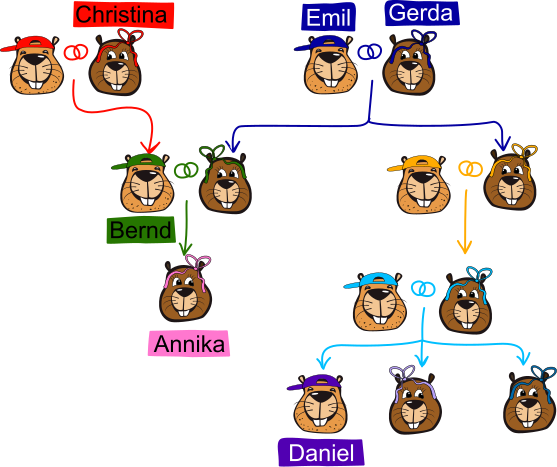
Daniel kirjeldab sugulusseoseid valemitena:

• isa(X) tähendab "kopra X isa";
• ema(X) tähendab "kopra X ema".

Näiteks, Annika isa on Bernd ja Berndi ema Christina. Seda võib valemitena märkida nii:

• isa(Annika) = Bernd
• ema(Bernd) = Christina
• ema(isa(Annika)) = Christina

Daniel peab peolt lahkuma enne kui ta oma kirjelduse lõpetab.

Küsimus

Kuidas peaks Annika ja Danieli sugulust valemitega kirjeldama?

[Interaktiivne]

(Lohista hallidesse lünkadesse õiged sõnad.)

15. Must-valge kunst

Üks kunstnik loob mustadest ja valgetest ruutudest koosnevaid mosaiike.

Ta kasutab oma teoste loomiseks erinevaid töövahendeid. Üks neist on programm, mis kombineerib kaks ühesuurust pilti järgmiste reeglite järgi:

• Need ruudud, mis on algsetes piltides sama värvi (mõlemad mustad või mõlemad valged), on uues pildis valged.
• Need ruudud, mis on algsetes piltides eri värvi (üks must, teine valge), on uues pildis mustad.

Nüüd annab kunstnik sellele programmile sisendiks järgmised pildid:

Küsimus

Milline on tulemus?

[Raadionupud]

A. B. C. D.