1. Imeline masin

Kobrastel on imeline masin. Sellesse pannakse ülevalt sisse viis arvu, näiteks 3, 2, 4, 5 ja 1.

Edasi liiguvad arvud mööda nooli ja läbi lülide allapoole, kuni jõuavad kõige all olevatesse väljundpesadesse.

Iga lüli võrdleb kaht sissetulevat arvu ning suunab väiksema arvu edasi vasakpoolse ja suurema parempoolse noole suunas. Siin on üks näide:

Küsimus

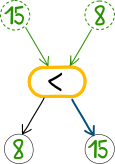
Kuidas arvud 3, 2, 4, 5 ja 1 väljundpesadesse paigutuvad?

[Interaktiivne]

(Lohista arvud õigetesse väljundpesadesse.)

2. Pakirobotid

Meelil on logistikafirma ja sellel neli pakkide sorteerimiskeskust. Igas keskuses toimetavad robotid pakke antud lähtekohtadest antud sihtkohtadesse vastavalt neile saadetud käsujadadele.

Robotid alustavad kollastelt ruutudelt nooltega näidatud suundades. Edasi liiguvad robotid järgmiselt:

Kui robot on hallil ruudul , liigub ta otse edasi kuni jõuab seinani või teist värvi ruudule.
Kui robot on sinisel ruudul , pöörab ta vasakule (L) või paremale (R) vastavalt järgmisele käsule saadud käsujadas. Kui robot on sinisel ruudul ja käsk suunab ta vastu seina, pöörab robot seina ees ümber ja liigub vastassuunas:
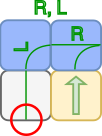
Kui robot jõuab rohelisele ruudule , jääb ta seisma ja rohkem käske ei täida.

Küsimus

Millise käsujada peaks Meeli robotitele saatma, et kõik neli robotit jõuaks selle järgi liikudes rohelistele ruutudele?

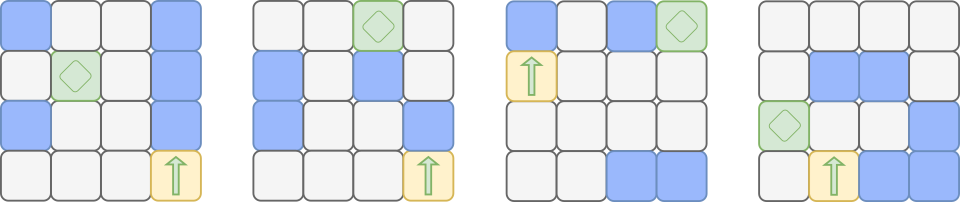
[Raadionupud]

A. L, L, R, L, L

B. L, R, R, L, L

C. R, L, R, R, L

D. R, R, L, L, R

3. Sadeveetorustik

Kopralinnas on mägedes seitse vihmavee kogumise tiiki. Paduvihmade ajal täituvad tiigid kiiresti ja võivad üle ääre ajama hakata. Tiikidel olevad arvud näitavad, kui palju vett tuleb igast tiigist ära juhtida, et üleujutust vältida.

Linnavalitsus plaanib ehitada uue torustiku, mis ühendaks kõik seitse tiiki linna peamise veehoidlaga. Torustik peab tagama, et kõigi tiikide üleliigne vesi jõuaks veehoidlasse.

Insenerid on kaardistanud võimalikud toruühendused tiikide ja veehoidla vahel. Igal toruühendusel on kindel läbilaskevõime (veehulk, mida selle kaudu saab ära juhtida) ja hind, mis on toruühenduse läbilaskevõime korda miljon eurot.

Linnavalitsus tahab ehitada torustiku, mis

ühendab kõik seitse tiiki veehoidlaga (kas otse või läbi teiste tiikide);
tagab kõigis toruühendustes vajaliku läbilaskevõime, et paduvihmaga toime tulla;
saavutab selle vähima võimaliku kuluga.

Küsimus

Millised toruühendused peaks selleks ehitama?

[Interaktiivne]

(Toruühenduse valimiseks kliki sellel oleval ringil. Valiku tühistamiseks kliki uuesti.)

4. Rahavahetus

Kobrastel on Suure Tammi juures vahetuspunkt, kus saab münte vahetada erinevates suurustes okste vastu. Allpool on näha vahetuskursid. On teada, et kobrastel on igas suuruses oksi piisav hulk.

Suurt hulka väikseid oksi on tülikam kaasas kanda kui väiksemat hulka suuremaid oksi. Sellepärast koostab Bruno eeltoodud vahetuskursside põhjal tabelit, kus iga müntide arvu kohta on kirjas vähim okste arv, milleks selle vahetada saab:

Münte	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
Oksi	1	2	3	4	5	1	2	1	2	3	4	2	1	2

Tabeli koostamisel paneb Bruno tähele, et paremal uute lahtrite täitmisel saab kasutada vasakul juba täidetud lahtreid. Näiteks 11 münti on võimalik vaadata kui 8+3 või 6+5 või 1+10 münti.

Küsimus

Mis on vähim okste arv, milleks saab vahetada 17 münti?

[Täisarv]

5. Maagiline klahv

Arturo arvuti klaviatuuril on lisaks tavalistele ka üks maagiline klahv.

Selle klahviga on seotud loendur M, mille väärtus suureneb ühe võrra iga kord kui klahvi vajutada, ja seejärel kirjutatakse logifaili järjest arvud M, M-1, ..., 1.

Selle klahvi viie esimese vajutuse tulemused on järgmised:

M	Logifaili sisu
1	1
2	1, 2, 1
3	1, 2, 1, 3, 2, 1
4	1, 2, 1, 3, 2, 1, 4, 3, 2, 1
5	1, 2, 1, 3, 2, 1, 4, 3, 2, 1, 5, 4, 3, 2, 1

Arturo vajutas klahvi veel päris palju kordi ja nüüd on tal logifailis suur hulk arve.

Küsimus

Milline arv on logifailis 127. kohal?

[Täisarv]

6. Kosmiline kiirgus

Marina pangakontoga juhtus imelik lugu. Ta vaatas oma kontojääki ja see oli 8095€. Hetke pärast vaatas ta uuesti ja see oli 7071€, kuigi ta polnud vahepeal mingeid makseid ega ülekandeid teinud. Ta kirjutas kohe panka, et uurida, milles on asi.

Pank leidis uurimise järel, et tegu polnud ei tarkvaravea ega ka küberründega. Muutuse põhjus tundus olevat juhuslik viga arvutisüsteemi mälus, mille võis põhjustada näiteks kosmiline kiirgus.

Arvuti mälus hoitakse arve kahendsüsteemis. See süsteem kasutab arvude märkimiseks ainult numbreid 0 ja 1 ning paremalt vasakule liikudes on iga järgmise positsiooni kaal eelmisest kaks korda suurem.

Allolev näide selgitab, kuidas leida 8-bitise 2-süsteemi arvu 00100011 väärtus:

Positsioon	8	7	6	5	4	3	2	1
Kaal	128	64	32	16	8	4	2	1
Bitt	0	0	1	0	0	0	1	1
Väärtus	0	0	32	0	0	0	2	1

Kokku on 2-süsteemi arvu 00100011 väärtus 32+2+1=35.

Vaatame nüüd, mis juhtub, kui selles arvus 8. positsioonil oleva biti väärtus muutub:

Positsioon	8	7	6	5	4	3	2	1
Kaal	128	64	32	16	8	4	2	1
Bitt	1	0	1	0	0	0	1	1
Väärtus	128	0	32	0	0	0	2	1

Muudetud arvu väärtus on 128+32+2+1=163.

Nagu näha, võib ühe biti muutmine arvu väärtust päris palju mõjutada!

Küsimus

Milline bitt ja kuidas pidi muutuma Marina kontojäägis?

[Raadionupud]

A. 11. positsioonil olev bitt 1-st 0-ks

B. 12. positsioonil olev bitt 1-st 0-ks

C. 11. positsioonil olev bitt 0-st 1-ks

D. 12. positsioonil olev bitt 0-st 1-ks

7. Emili lilled

Emili kasvatab aias lilli, millel on igaühel kolm tunnust:

õie kuju võib olla tulbi, liilia või karikakra moodi;
õie värv võib olla must, valge või hall;
varrel võib olla null, üks või kaks lehte.

Emili jagab alati oma lilled vaaside vahel nii, et kõigis vaasides on võrdne arv lilli.

Lisaks tahab ta, et ühes vaasis koos olevatel lilledel oleks kõigil vähemalt üks ühine tunnus: kõik ühes vaasis olevad lilled on sama õite kujuga või sama õite värviga või sama arvu lehtedega vartel.

Praegu on tal kuus lille vaasides nii, et erinevates vaasides on lilledel erinevad ühised tunnnused (esimeses vaasis ühine õite värv, teises vaasis samuti ühine õite värv, aga kolmandas vaasis ühine lehtede arv):

Nüüd võtab ta kolm lille juurde ja tahab kõik üheksa lille jagada kolme vaasi vahel nii, et ühine tunnus oleks kõigis kolmes vaasis sama. Kolm uut lille on:

Küsimus

Milline järgmistest joonistest kujutab üht Emily kolmest vaasist pärast kõigi üheksa lille paigutamist?

[Raadionupud]

A. B. C. D.

8. Salakiri

Georg leiutas salakirjasüsteemi, kus iga sõna kodeerimine toimub kahes etapis:

Esimeses etapis vaadatakse sõna läbi vasakult paremale ja võetakse tulemusse paaritutel positsioonidel (esimene, kolmas, viies jne) olevad tähed selles järjekorras. Näiteks sõnast bread saab selles etapis bed.
Teises etapis vaadatakse sõna läbi paremalt vasakule ja lisatakse eelmise etapi tulemuse lõppu kõik need tähed, mis enne välja jäid, nende vaatamise järjekorras. Näiteks sõnast bread saab teise etapi lõpuks bedar.

Georg pani tähele, et kui ta rakendab seda kodeerimismeetodit sõnale mitu korda järjest, saab ta esialgse sõna tagasi. Näiteks sõnast milk saab mlki, sõnast mlki saab mkil ja sõnast mkil saab jälle milk. Seega saab ta sel juhul esialgse sõna tagasi kolme järjestikuse kodeerimisega.

Küsimus

Mitme kodeerimisega saab ta esialgse sõna tagasi, kui alustab sõnast society?

[Täisarv]

9. Advendiküünlad

Kristol on traditsioon süüdata advendi ajal küünlaid: esimesel advendil üks küünal, teisel advendil kaks jne.

Advendiaja alguses on Kristol neli ühepikkust küünalt. Tal oleks hea meel, kui ta saaks küünlaid süüdata nii, et need oleks ka advendiaja lõpuks ühepikkused. Selleks peaks iga küünal kokku põlema sama arvu päevi. Aga tuleb välja, et neli nädalat kestva advendi puhul pole see kahjuks võimalik.

Kui advent kestaks kolm nädalat, võiks Kristo küünlaid süüdata näiteks nii (iga küünal põleb kaks päeva):

Küsimus

Kuidas peaks Kristo küünlaid süütama, kui advent kestaks viis nädalat?

[Interaktiivne]

(Küünla süütamiseks või kustutamiseks kliki sellel.)

10. Kõige kulunum segment

Tavaline digitaalne kell näitab aega nelja numbriga ja muudab näitu iga minuti järel.

Iga numbrit näidatakse seitsmest segmendist koosneva indikaatoriga. Selline indikaator näitab numbreid 0 kuni 9 järgmiselt:

Segmendid kuluvad iga kord, kui neid väljalülitatud olekust uuesti sisse lülitatakse. Segment, mida on kõige rohkem kordi sisse lülitatud, tuleb ka esimesena välja vahetada.

Küsimus

Milline segment tuleb esimesena välja vahetada?

(Sisesta segmendi tähisena üks number ja üks täht vastavalt allolevale skeemile.)

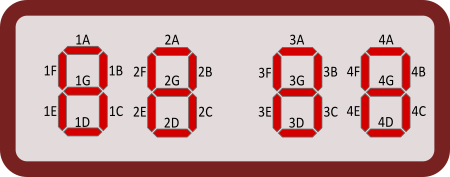
[Tekstikast]

11. Voltimismäng

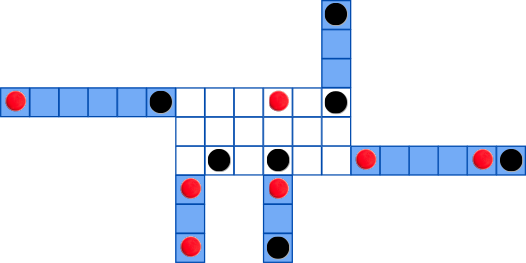
Luca mängib arvutis voltimismängu, kus iga tase koosneb 3×6 valgest ruudustikust, mille mõne rea ja veeru otsas on sinised lisaribad.

Nii ruudustikus kui lisaribades võib iga ruut olla tühi või sisaldada musta auku või punast punni.

Igal tasemel on mängija eesmärk voltida lisaribad ruudustiku peale nii, et lõpuks oleks tulemuseks tühi 3×6 ruudustik.

Ribade voltimisel kehtivad järgmised reeglid:

Kui voltimisel satuvad kohakuti kaks tühja ruutu, on tulemuseks tühi ruut.
Kui voltimisel satuvad kohakuti kaks auguga ruutu, on tulemuseks auguga ruut.
Kui voltimisel satuvad kohakuti tühi ruut ja auguga ruut, on tulemuseks auguga ruut.
Kui voltimisel satuvad kohakuti auguga ruut ja punniga ruut, on tulemuseks tühi ruut.
Voltimine, kus kohakuti satuvad tühi ruut ja punniga ruut, ei ole lubatud.
Voltimine, kus kohakuti satuvad kaks punniga ruutu, ei ole lubatud.

Küsimus

Mitu erinevat voltimisjärjekorda on võimalikud alloleva taseme lahendamiseks?

[Täisarv]

12. Häkaton

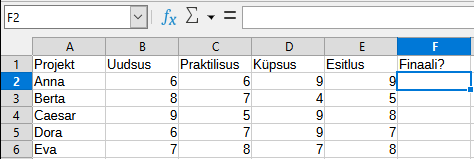
Häkatonid on Kopramaal populaarsed ja eelvoorudes osaleb sadu võistkondi. Žüriid hindavad iga projekti 10-palli süsteemis nelja kriteeriumi alusel: idee uudsus, teostuse praktilisus, prototüübi küpsus, esitlus.

Et vältida vigu finaali kutsumises, otsustas peakohtunik selle automatiseerida. Ta sisestas kõik hinded suurde tabelisse, kirjutas selle lahtrisse F2 valemi
=IF(OR(AND(B2>=7;C2>=7);SUM(B2:E2)>30);"jah";"ei")
ja kopeeris selle valemi alla kogu veeru F ulatuses.

Selgituseks valemis kasutatud funktsioonide kohta:

IF(tingimus;väärtus1;väärtus2) kui tingimus kehtib, on tulemus väärtus1; kui tingimus ei kehti, on tulemus väärtus2;
OR(tingimus1;tingimus2) kehtib, kui kehtib kas tingimus1 või tingimus2 või mõlemad;
AND(tingimus1;tingimus2) kehtib, kui tingimus1 ja tingimus2 mõlemad kehtivad;
SUM(lahter1;lahter2) liidab kokku kõik arvud ristkülikus, mille vasak ülemine nurk on lahter1 ja parem alumine nurk lahter2 (lahter1 ja lahter2 kaasa arvatud).

Küsimus

Millised ekraanipildil näha olevast viiest võistkonnast kutsutakse finaali?

(Märgi kõik õiged vastused.)

[Märkeruudud]

A. Anna

B. Berta

C. Caesar

D. Dora

E. Eva

13. Sisukord

Bioloogiatunniks teeb Kaarel referaati lindudest ja loomadest. Referaadi sisukorda ei tee ta käsitsi, vaid laseb selle genereerida tekstitöötlusprogrammil.

Selleks märgib ta imetajate ja lindude peatükkide pealkirjad laadiga Pealkiri 1 (ingl Heading 1). Töös vaadeldud imetajate (rebane, hunt, jänes, kobras) jaotiste pealkirjad märgib ta laadiga Pealkiri 2 (ingl Heading 2). Kobraste jaotises on kaks alamjaotist, mis on ka sisukorras kajastatud.

Küsimus

Täna lisas Kaarel referaati jäneste jaotisse alamjaotised valgejänesest, halljänesest ja ameerika jänesest.

Kuidas peaks nende pealkirjad vormistama, et nad sisukorras õigesti kajastuksid?

[Raadionupud]

A. Need peaks märkima laadiga Pealkiri 1

B. Need peaks märkima laadiga Pealkiri 2

C. Need peaks märkima laadiga Pealkiri 3

D. Need peaks märkima laadiga Pealkiri 4

14. Kobras Jones

Kuulus seiklejakobras Jones uurib püramiidi, kus on palju ohtlikke käike. Iga käigu lõpus on aare. Kui Jones läheb käiku, tahab ta võimalikult kiiresti aardeni jõuda.

Igas käigus on hulk plokke. Alguses on kõik plokid all. Kui keegi käigu algusse ilmub, hakkavad plokid perioodiliselt liikuma. Plokk perioodiga 2 liigub 2 minuti pärast üles, järgmise 2 minuti pärast alla, järgmise 2 minuti pärast jälle üles jne.

Jones võib ühe ploki alt teise alla liikuda ainult siis, kui mõlemad plokid ja kõik nende vahel olevad plokid on üleval. Aga ta on väga väle ja võib eeldada, et ühe ploki alt teise alla jooksmiseks tal üldse aega ei kulu.

Vaatame vasakul olevat näidet.

Selles käigus on kaks plokki, A perioodiga 2 ja B perioodiga 3. Joonisel on kujutatud plokkide liikumist Jonesi käiku saabumise järgsetel minutitel.

Joonisel käitub Jones, nagu ta järgiks järgmisi käske:

    oota(2)
    mine_plokini(A)
    oota(1)
    mine_aardeni

Jones oleks võinud aardeni jõuda sama ajaga ka lühema käsujadaga:

    oota(3)
    mine_aardeni

Küsimus

Järgmises käigus on neli plokki perioodidega 3, 5, 8 ja 4.

Milline on lühim käsujada, millega Jones jõuab aardeni minimaalse ajaga?

[Interaktiivne]

(Lohista käsud halli alasse ja täida neis lüngad õigete väärtustega. Käigu all olevate nooltega saad simuleerida plokkide liikumist minutite kaupa.)

15. Numbrimäng

Gemmal on koolis igav ja ta joonistab ruudulisele paberile numbrite kujutised:

Edasi hakkab ta numbreid kombineerima: kahest numbrist uue kujundi loomisel värvib ta mustaks täpselt need ruudud, millele vastavad ruudud on neis kahes numbris erivärvilised.

Näiteks oma lemmikarvu 42 numbrite kombineerimisel saab ta sellise tulemuse:

+ =

Küsimus

Millise kahekohalise arvu numbrite kombineerimisel saab Gemma alloleva tulemuse?

(Kui võimalikke vastuseid on mitu, sisesta ükskõik milline neist.)

[Tekstikast]