У бобров есть магический аппарат. Сверху в него загружаются пять чисел, например, 3, 2, 4, 5 и 1.
Далее числа движутся вниз по стрелкам и через элементы 
, пока не достигают самых нижних выходных слотов.
Каждый элемент сравнивает два входящих числа и направляет меньшее число дальше по левой стрелке, а большее — по правой. Вот один пример:
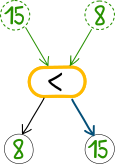
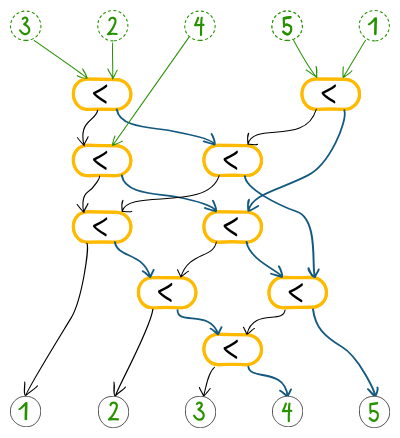
Как в выходных слотах будут располагаться числа 3, 2, 4, 5 и 1?
[Interaktiivne]
(Перетащи числа в правильные выходные слоты.)
Правильный ответ:
Маша владеет логистической компанией, которая располагает четырьмя центрами сортировки посылок. В каждом центре роботы доставляют посылки из пункта отправления в пункт назначения в соответствии с заданными последовательностями команд.
Роботы начинают движение из жёлтых квадратов 
в направлениях, указанных стрелками. Далее роботы движутся следующим образом:
Если робот находится на сером квадрате 
, он движется прямо, пока не достигнет стены или квадрата другого цвета.
Если робот находится на синем квадрате 
, он поворачивается налево (L) или направо (R) в соответствии с командой, которая идёт следующей в последовательности команд. Если робот находится на синем квадрате, и команда направляет его к стене, то перед стеной робот разворачивается и двигается в противоположном направлении:
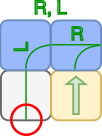
Когда робот оказывается на зеленом квадрате 
, он останавливается и больше не выполняет ни одну из команд.
Какую последовательность команд Маша должна передать роботам, чтобы все четыре робота, следуя полученным командам, смогли добраться до зелёных квадратов?
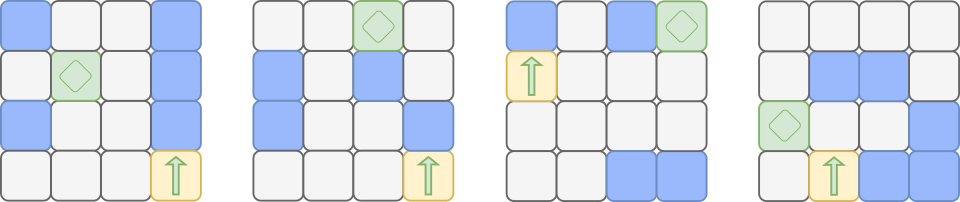
[Raadionupud]
A. L, L, R, L, L
B. L, R, R, L, L
C. R, L, R, R, L
D. R, R, L, L, R
Правильный ответ: D.
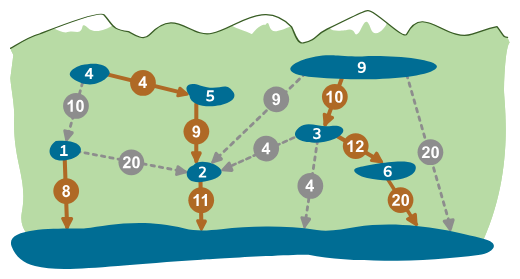
В горах Бобруйска расположено семь прудов для сбора дождевой воды. Во время сильных дождей пруды быстро наполняются, и вода может перелиться через край. Числа на прудах указывают, сколько воды необходимо слить из каждого пруда, чтобы предотвратить наводнение.
Городская администрация хочет построить систему труб, которая соединила бы все семь прудов с главным городским водохранилищем. Система должна обеспечить, чтобы избыточная вода из всех прудов поступала в водохранилище.
Инженеры разработали схему с возможными соединениями труб между прудами и водохранилищем. Каждая труба имеет определённую пропускную способность (объём воды, которое может быть через неё отведено) и стоимость, которая равна пропускной способности трубы, умноженной на один миллион евро.
Администрация хочет построить систему труб, которая
Какие трубы следует построить для этого?
[Interaktiivne]
(Щёлкни на кружок, чтобы выбрать соответствующую трубу. Для отмены выбора снова щёлкни на него.)
Правильный ответ:
У бобров на Великой Плотине есть пункт обмена, где можно обменять монеты на ветки разных размеров. Ниже приведены курсы обмена. Известно, что у бобров достаточное количество веток всех размеров.
Носить большое количество маленьких веток гораздо сложнее, чем меньшее количество больших веток. Поэтому, используя вышеприведённые курсы обмена, Бруно составил таблицу, где каждому количеству монет соответствует наименьшее количество получаемых веток:
| Количество монет | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| Количество веток | 1 | 2 | 3 | 4 | 5 | 1 | 2 | 1 | 2 | 3 | 4 | 2 | 1 | 2 |
При составлении таблицы Бруно заметил, что при заполнении новых расположенных справа ячеек можно использовать уже заполненные ячейки слева. Например, 11 монет можно рассматривать как 8+3, 6+5 или 1+10 монет.
Какое наименьшее количество веток можно получить за 17 монет?
[Täisarv]
Правильный ответ: 3 ветки.
Помимо обычных клавиш на клавиатуре Артура можно найти одну магическую клавишу.
С этой клавишей связан счётчик M. При каждом нажатии на магическую клавишу значение счётчика увеличивается на одну единицу, а в лог-файл последовательно записываются числа M, M-1, ..., 1.
Результаты первых 5 нажатий на эту клавишу выглядят следующим образом:
| M | Содержание лог-файла |
|---|---|
| 1 | 1 |
| 2 | 1, 2, 1 |
| 3 | 1, 2, 1, 3, 2, 1 |
| 4 | 1, 2, 1, 3, 2, 1, 4, 3, 2, 1 |
| 5 | 1, 2, 1, 3, 2, 1, 4, 3, 2, 1, 5, 4, 3, 2, 1 |
Артур много раз нажимал на магическую клавишу, и теперь в лог-файле скопилось большое количество чисел.
Какое число находится в лог-файле на 127 месте?
[Täisarv]
Правильный ответ: 10.
С банковским счётом Марины произошло нечто странное. Она проверила остаток на своём счету и увидела 8095€. Через мгновение она вновь проверила остаток счёта, но обнаружила 7071€, хотя за это время она не совершила никаких платежей или переводов. Она немедленно написала в банк, чтобы выяснить, в чём дело.
После расследования банк установил, что это не было ни программной ошибкой, ни кибератакой. По всей видимости, причиной изменения стала случайная ошибка в памяти компьютерной системы, которая могла быть вызвана, например, космическим излучением.
В памяти компьютера числа хранятся в двоичной системе. Для представления чисел эта система использует только цифры 0 и 1, и при движении справа налево каждая последующая позиция имеет вдвое больший вес, чем предыдущая.
Нижеприведённый пример демонстрирует, как в двоичной системе счисления найти значение 8-битного числа 00100011:
| Позиция | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
| Вес | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| Бит | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 |
| Значение | 0 | 0 | 32 | 0 | 0 | 0 | 2 | 1 |
Таким образом, в двоичной системе счисления значение числа 00100011 равно 32+2+1=35.
Теперь посмотрим, что произойдёт, если в этом числе изменить значение 8-го бита:
| Позиция | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
| Вес | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
| Бит | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 1 |
| Значение | 128 | 0 | 32 | 0 | 0 | 0 | 2 | 1 |
Значение изменённого числа равно 128+32+2+1=163.
Как видим, изменение всего одного бита может существенно повлиять на значение числа!
Какой бит и каким образом должен был измениться на Маринином счёте с остатком?
[Raadionupud]
A. Расположенный на 11-ой позиции бит изменился с 1 на 0
B. Расположенный на 12-ой позиции бит изменился с 1 на 0
C. Расположенный на 11-ой позиции бит изменился с 0 на 1
D. Расположенный на 12-ой позиции бит изменился с 0 на 1
Правильный ответ: A.
Эмилия выращивает в саду цветы. У каждого цветка есть три признака:
Эмилия всегда расставляет цветы по вазам так, чтобы в каждой вазе оказалось одинаковое количество цветов.
Она также хочет, чтобы цветы, оказавшиеся в одной и той же вазе, имели хотя бы один общий признак: все оказавшиеся в одной вазе цветы должны иметь или одну и ту же форму лепестков, или лепестки должны быть одинакового цвета, или стебли должны быть с одинаковым количеством листков.
Сейчас шесть цветов оказались в вазах таким образом, что у цветов, оказавшихся в разных вазах, имеются разные общие признаки — в первой вазе оказались цветы, где лепестки одинакового цвета, во второй вазе также оказались цветы, где лепестки одинакового цвета, а в третьей вазе оказались цветы с одинаковым количеством листков:
Теперь Эмилия берёт ещё три цветка и хочет расставить все девять цветов по трём вазам таким образом, чтобы общий признак был одинаковым во всех трёх вазах. Три новых цветка:
Какой из следующих рисунков изображает одну из трёх ваз Эмилии после того, как все девять цветов будут расставлены?
[Raadionupud]
A. 
B. 
C. 
D. 
Правильный ответ: C.
Георг изобрёл систему шифрования, в которой каждое слово шифруется в два этапа:
На первом этапе слово сканируется слева направо. В результат последовательно записываются буквы, находящиеся на нечётных позициях (первая, третья, пятая и т. д.). Например, слово bread на этом этапе становится bed.
На втором этапе слово сканируется справа налево. Все ранее пропущенные буквы добавляются по мере их прочтения в конец результата, полученного на предыдущем этапе. Например, слово bread в конце второго этапа становится bedar.
Георг заметил, что если он несколько раз подряд применит эту систему шифрования к слову, то получит обратно исходное слово. Например, слово milk станет mlki, слово mlki становет mkil, а слово mkil станет вновь milk. В этом случае он получит обратно исходное слово за три последовательных шифрования.
За сколько последовательных шифрований он получит обратно исходное слово, если этим словом будет society?
[Täisarv]
Правильный ответ: За 6 последовательных шифрований.
У Кристо есть традиция зажигать свечи в период адвентов: в первый адвент от зажигает одну свечу, во второй — две и так далее.
В начале периода адвентов у Кристо есть четыре свечи одинаковой длины. Он был бы рад, если бы мог зажигать свечи таким образом, чтобы и к концу периода адвентов они оставались одинаковой длины. Для этого каждая свеча должна была бы гореть одинаковое количество дней. Но период адвентов длится четыре недели, и поэтому это, к сожалению, невозможно.
Если бы период адвентов длился три недели, Кристо мог бы зажигать свечи следующим образом (каждая свеча горит два дня):
Как Кристо должен был бы зажигать свечи, если бы период адвентов длился пять недель?
[Interaktiivne]
(Щёлкни на свечу, чтобы зажечь или потушить её.)
Один из возможных правильных ответов:
В обычных цифровых часах время показывается с помощью четырёх цифр. Время меняет своё значение каждую минуту.
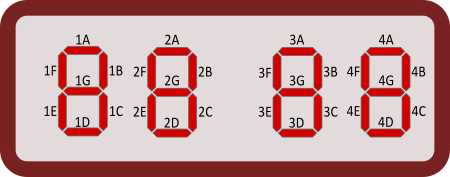
Каждая цифра отображается с помощью индикатора, состоящего из семи сегментов. Такой индикатор показывает цифры от 0 до 9 следующим образом:
Сегменты изнашиваются каждый раз, когда их активируют из выключенного состояния во включённое. Сегмент, который активируется чаще всего, подлежит и замене в первую очередь.
Какой сегмент необходимо заменить в первую очередь?
(Для обозначение сегмента запиши одну цифру и одну букву в соответствии с нижеприведённой схемой.)
[Tekstikast]
Правильный ответ: 4E.
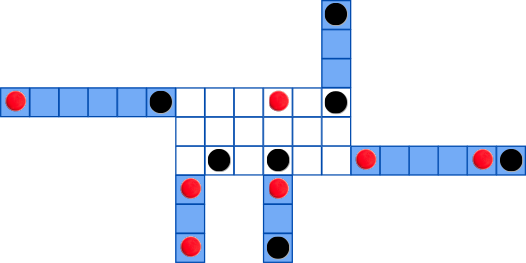
Лука играет в компьютерную игру на складывание, где на каждом уровне квадраты образуют белую сетку размером 3×6. На концах некоторых строк и столбцов этой сетки есть дополнительные синие полоски.
Как на самой сетке, так и на дополнительных полосках, каждый квадрат может быть пустым, содержать чёрное отверстие или красный выступающий элемент.
На каждом уровне цель игрока — сложить дополнительные полоски на сетку так, чтобы в итоге получилась пустая сетка размером 3×6.
К складыванию полосок применяются следующие правила:
Сколько существует различных последовательностей складывания, необходимых для прохождения нижеприведённого уровня?
[Täisarv]
Правильный ответ: 6.
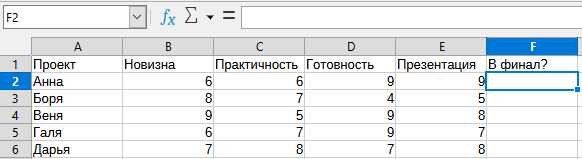
Хакатоны пользуются популярностью в Бобруйске, и в предварительных турах участвуют сотни команд. Жюри оценивает каждый проект по 10-балльной системе на основе четырёх критериев: новизна идеи, практичность реализации, степень готовности прототипа и презентация.
Во избежание ошибок при приглашении команд в финал, главный судья решил автоматизировать этот процесс. Он внёс все оценки в большую электронную таблицу, записал в табличную ячейку F2 формулу
=IF(OR(AND(B2>=7;C2>=7);SUM(B2:E2)>30);"да";"нет")
и скопировал её по всему столбцу F.
Объяснения об использованных в формуле функциях:
IF(условие;значение1;значение2) — если условие выполняется, то результатом будет значение1; если условие не выполняется, то результатом будет значение2;OR(условие1;условие2) — выполняется, если выполняется либо условие1, либо условие2, либо оба эти условия;AND(условие1;условие2) — выполняется, если выполняются оба условия, то есть и условие1, и условие2;SUM(ячейка1;ячейка2) — складывает все числа, находящиеся в прямоугольником зоне, у которой левый верхний угол находится в ячейке1, а правый нижний угол находится в ячейке2 (ячейка1 и ячейка2 тоже входят в эту прямоугольную зону).Какие из пяти команд, показанных на вышеприведённом рисунке, получат приглашение в финал?
(Отметь все правильные ответы.)
[Märkeruudud]
A. Анна
B. Боря
C. Веня
D. Галя
E. Дарья
Правильный ответ: B, C, E.
Для урока биологии бобр Витя пишет реферат о птицах и животных. Содержание реферата он не стал писать вручную, а воспользовался возможностью его генерирования с помощью текстового редактора.
Для этого заголовки глав о млекопитающих и птицах он обозначил стилем Заголовок 1 (англ Heading 1). Заголовки разделов, где рассмотриваются млекопитающие (лиса, волк, заяц, бобр), он обозначил стилем Заголовок 2 (англ Heading 2). В разделе о бобрах есть два подраздела, которые также должны быть видны в содержании.
Сегодня Витя добавил в реферат в раздел о зайцах подразделы о белом, сером и американском зайцах.
Как следует оформить эти заголовки, чтобы они правильно отобразились в содержании?
[Raadionupud]
A. Их следует обозначить стилем Заголовок 1
B. Их следует обозначить стилем Заголовок 2
C. Их следует обозначить стилем Заголовок 3
D. Их следует обозначить стилем Заголовок 4
Правильный ответ: C.
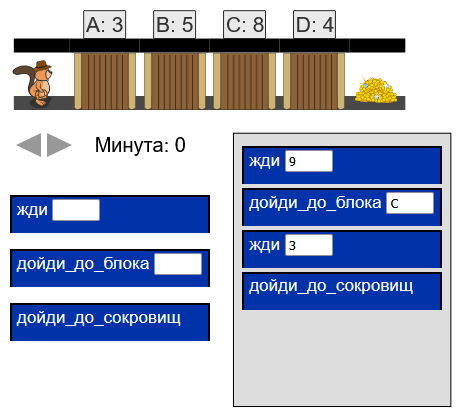
Знаменитый искатель приключений бобр Джонс 
исследует пирамиду со множеством опасных туннелей. В конце каждого туннеля находится сокровище. Оказавшись в туннеле, Джонс стремится как можно быстрее добраться до сокровища.
Внутри каждого туннеля есть набор блоков. Изначально все блоки опущены. Когда кто-то появляется в начале туннеля, блоки автоматически приводятся в периодическое движение. Например, блок с периодом 2 поднимается вверх через 2 минуты, через следующие 2 минуты опускается вниз, затем вновь через следующие 2 минуты поднимается вверх и так далее.
Джонс может перемещаться из-под одного блока под другой только в том случае, если оба блока и все блоки между ними подняты. Но он очень ловок, и можно считать, что он перемещается из-под одного блока под другой мгновенно, вообще не тратя на это времени.
|
Рассмотрим пример, приведённый с левой стороны. В этом туннеле есть два блока, A с периодом 2 и B с периодом 3. На рисунке показано движение блоков в течение нескольких минут после того, как Джонс оказался в туннеле. На рисунке Джонс ведёт себя так, как будто он выполняет следующие команды:
жди(2)
дойди_до_блока(A)
жди(1)
дойди_до_сокровищ
Джонс мог бы добраться до сокровищ за то же время, но используя более короткую последовательность команд:
жди(3)
дойди_до_сокровищ
|
В следующем туннеле располагаются четыре блока с периодами 3, 5, 8 и 4.
Какая кратчайшая последовательность команд позволит Джонсу добраться до сокровища за минимальное время?
[Interaktiivne]
(Перетащи команды в серое поле и заполни имеющиеся в командах пробелы правильными значениями. С помощью расположенных под туннелем стрелками ты можешь симулировать движение блоков по минутам.)
Правильный ответ:
Диме скучно на уроке, и он рисует цифры на бумаге в клеточку:
Далее он начинает комбинировать цифры: создавая новую фигуру из двух цифр, он закрашивает чёрным цветом именно те клетки, которые в этих двух цифрах были окрашены по-разному.
Например, при комбинировании цифр своего любимого числа 42 он получает следующий результат:
+ = 
При комбинировании цифр какого двузначного числа Дима получит нижеприведённый результат?
(Если существует несколько возможных ответов, то запиши любой из них.)
[Tekstikast]
Правильный ответ: 62 или 26.
Copyright © 2025 Bebras – International Challenge on Informatics and Computational Thinking.
Licensed under Creative Commons Attribution-ShareAlike 4.0 International License.
Flag icons by GoSquared.